粗糙衰减因子在电磁波蒸发波导传播中的应用

芮国胜，郭 彦，田文飚

（海军航空工程学院电子信息工程系，山东 烟台 264001）

蒸发波导是一种特殊的表面波导，在我国东海和南海各海区是多发区，年出现概率为85%，且不同季节变化不明显[1-3]。电磁波可以被陷获在蒸发波导内，改变其传播轨迹实现超视距传播。这种反常传播现象容易对海上和海岸运作的微波雷达、通信和侦测等无线系统造成影响，已经引起中外学者的研究重视[4-5]。海面粗糙程度是引起电磁波传输衰减损耗的因素之一[6]，相关学者对Miller-Brown 近似模型进行了数值评估[7]，并结合粗糙海面的阴影效应分析了其对电磁波传播损耗的影响[8-9]。这些研究主要侧重于应用影响评估，对于模型中Bessel 函数的物理描述困难、级数展开形式复杂、需用数值模拟方法求解等问题，并未提出相关处理方案。本文结合我国实际海况数据，计算出蒸发波导最大陷获角，仿真分析了Miller-Brown 近似模型中粗糙衰减因子与海面风速和电波传播方向与海面夹角的关系。并通过射线描迹法仿真实验，得出蒸发波导高度确定时海面风速与粗糙衰减因子具有直接关系的结论。在假定条件下，运用高斯模型拟合得出Miller-Brown 模型的简化形式。高斯函数为初等函数，具有良好的统计分析特性，求解简单快速，该简化形式对快速掌握海面粗糙情况、分析进行其对电波传播衰减的影响有参考借鉴价值。

1 陷获角与粗糙衰减因子

大气波导的陷获角θc是指在一定大气参数条件下，电磁波能够被大气波导捕获形成大气波导陷获传播的最大仰角。其表达式为[10]

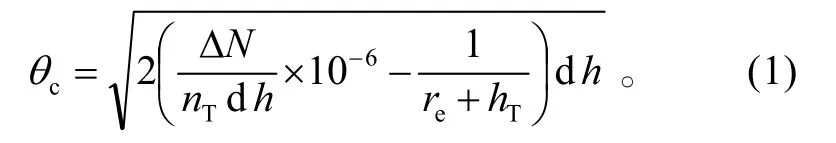
式(1)中：nT、re和hT分别为天线位置处的折射率、地球半径和天线高度；hd 为波导层厚度；NΔ 为波导层的折射率变化量。θc可以由波导强度近似表示

利用1982～1999年18 a 的海洋观测资料进行统计分析，参照世界气象组织WMO 的海域划分方法，得出各海区蒸发波导强度一般在35 M 左右[11]，由此计算出最大陷获角θcmax≈ 0.506°。

根据Miller-Brown 粗糙表面近似模型，可得到粗糙衰减因子表达式[12]：

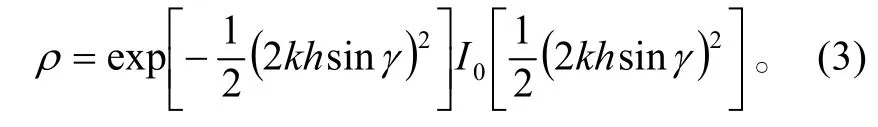
2 射线描迹法

射线描迹法是分析模拟电磁波在大气波导中传播路径的常用方法，是基于几何光学理论根据球面分层大气中的Snell 定律[2]推导得出。海拔高度分别为h1和h2处的修正折射指数m1和m2以及水平仰角θ1和θ2满足下式：

运用二阶泰勒级数展开并近似，得

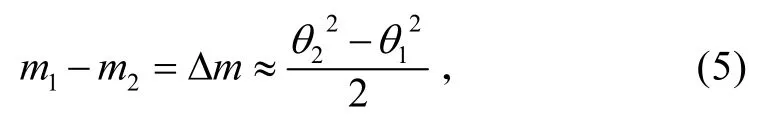
即

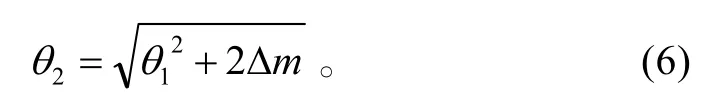
假设大气修正折射指数在h1和h2处是随高度呈线性变化的，且变化率为g，那么，

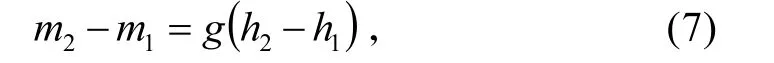
则由式(5)可得：

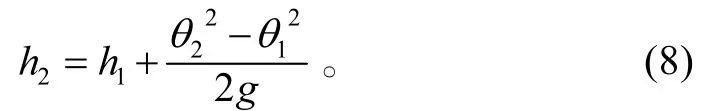
即

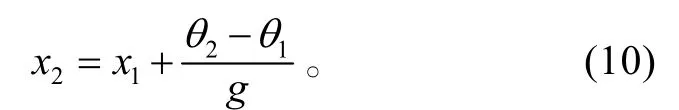
则式(6)、(8)、(10)为低仰角射线描迹方程。其射线轨迹示意图如图1 所示。

图1 射线轨迹示意图

3 仿真分析

通过matlab 仿真，分析风速和电磁波传播方向与海平面夹角对粗糙衰减因子的影响。本例中，选取实际应用的GPS 信号L1 波段。从图2 中可以看出：在海表面处，粗糙衰减因子随风速的增大而减小，在风速一定的情况下，电磁波传播方向与海平面夹角越大，减小得越快；且粗糙衰减因子随电磁波传播方向与海平面夹角的增大而减小，在夹角一定的情况下，风速越大减小得越快。

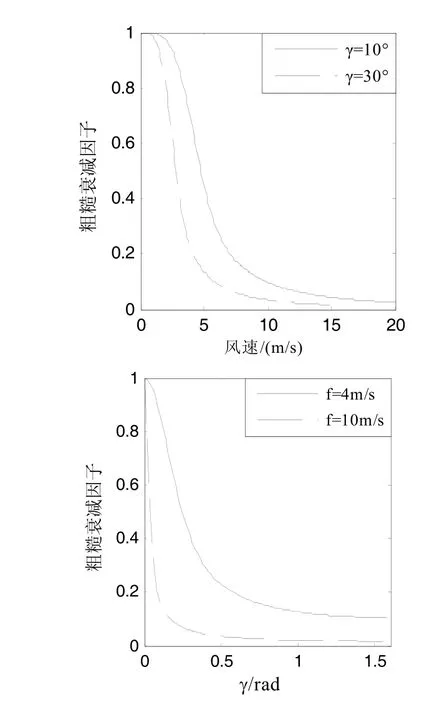
图2 风速和电磁波传播方向 与海平面夹角γ对粗糙衰减因子的影响

由于我国西沙海域夏季蒸发波导的平均高度在20～25 m 左右[13]。为此，设定蒸发波导高度为25 m，接收天线高度为5 m，运用射线描迹法，仿真分析GPS 信号在蒸发波导中的电波传播路径。

图3 蒸发波导修正折射率剖面下的射线追踪

仿真实验表明：当蒸发波导高度为25 m，天线高度在5～20 m 变化时，海面处电波传播方向与海平面的夹角γ在89.51～89.53°范围内变化。此时，可以得到海平面处风速对粗糙衰减因子的影响曲线如图4 所示。

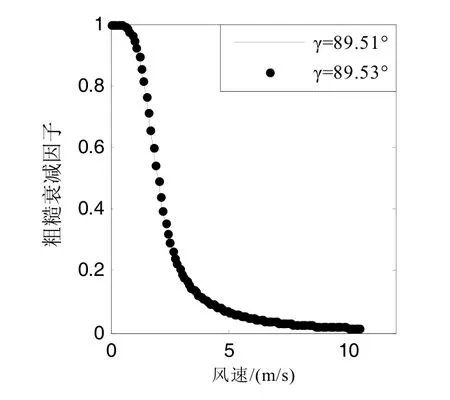
图4 风速对粗糙衰减因子的影响

从图4 从可以看出，当角度变化范围很小时，海面风速对粗糙衰减因子的影响几乎不变。由此可知：在我国海域范围内，只要已知蒸发波导高度，就可得到海面粗糙衰减因子与风速的直接关系。有利于快速获得海面粗糙状况，对分析电波的粗糙海面衰减有直接意义。

4 模型简化

第一类α阶Bessel 函数Jα(x)是Bessel 方程当α为整数或α非负时的解，须满足在x=0时有限，可定义为：

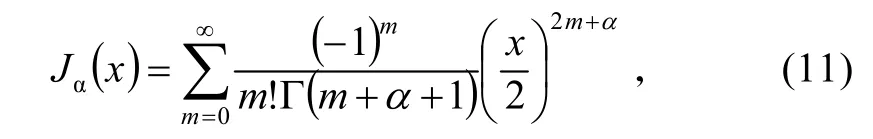
式中， Γ (z)为Γ 函数，可视为阶乘函数向非整型自变量的推广。

Bessel 函数当变量x为复数时同样成立，当x为纯虚数时能得到第一类修正Bessel 函数：

从上述公式中可以看出，Bessel 函数的级数展开形式复杂，特别是复宗Bessel 函数，往往要用数值模拟方法求解。为了简便实验研究过程，有必要在一定条件下对Miller-Brown 近似模型中这一复杂函数进行适当改进。为此，基于上文得到的结论，结合我国南海海域实际数据，进而对式(3)进行简化分析。

高斯函数属于初等函数，在统计学、光学、微波系统等学科领域都有广泛的应用，具有良好的数学分析特性，计算方便快捷。为此，选取高斯模型为目标函数并按如下步骤进行拟合：

2)运用最小二乘逼近法寻找最佳拟合曲线[14]；

3)综合考虑拟合精度及函数复杂度，最终确定拟合函数。

由此得到拟合函数表达式为：

从图5 可以看出，拟合后的曲线与理论曲线有良好的一致性。通过运算时间统计可以看出，简化后的模型在运算速度上相对于原模型提高了一个数量级，有效验证了该模型的计算简便特性。

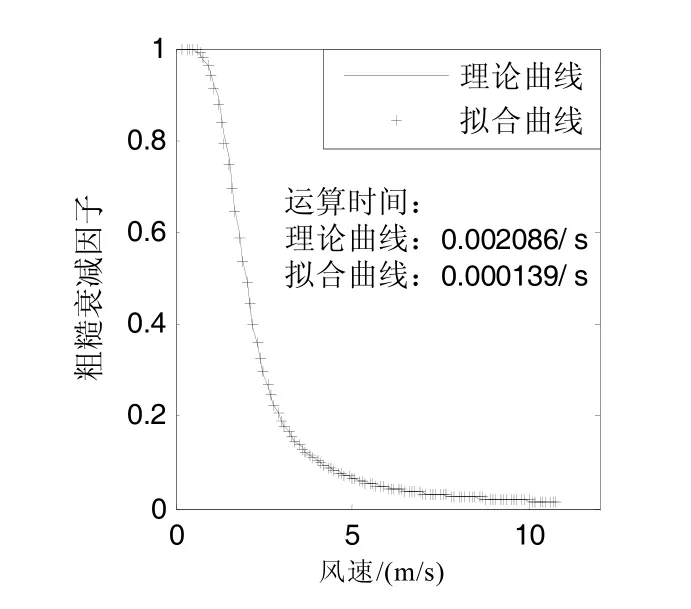
图5 高斯拟合曲线

5 结论

本文结合我国海洋蒸发波导实际数据，推算出其最大陷获角，对影响粗糙衰减因子的变量关系进行了仿真分析。利用射线描迹法，在假定蒸发波导高度的情况下，得出粗糙衰减因子与海面风速的直接关系，并针对Miller-Brown 近似模型中Bessel 函数求解复杂的问题运用高斯拟合模型对其进行了简化。该简化模型可分析性好，求解速度快、物理实现简便，有助于快速获得粗糙海面衰减因子数据，对研究分析粗糙海面对电磁波的衰减影响具有重要的参考价值。但本文的仿真分析还只局限于理论研究，下一步的主要工作是进行海上实地试验，利用实测数据来验证仿真结果并完善相关结论。

[1] 王喆, 王振会, 张玉生. 利用WRF 模式对海上蒸发波导的数值模拟研究[J]. 海洋技术, 2010,29(3)∶93-97.

[2] 王波. 基于雷达杂波和GNSS 的大气波导反演方法与实验[D]. 西安∶ 西安电子科技大学, 2009∶14-16.

[3] 成印河. 海上低空大气波导的遥感反演及数值模拟研究[D]. 北京∶ 中国科学院研究生院, 2009∶12-14.

[4] CAGLAR YARDIM. Statistical estimation and tracking of refractivity from radar clutter[D]. San Diego∶ University of California, 2007∶2-8.

[5] 刘成国. 蒸发波导环境特性和传播特征及其应用研究[D]. 西安∶ 西安电子科技大学, 2003∶14-18.

[6] 饶亲江, 龚中麟. 粗糙海面对高频雷达地波空间场分量传播损耗的影响[J]. 电子科学学刊, 2000,22(2)∶ 341-345

[7] DAVID E FREUND, NANCY E WOODS, HWAR- CHING KU, et al. Forward radar propagation over a rough sea surface∶ a numerical assessment of the Miller-brown approximation using a horizontally polarized 3GHz line source[J]. IEEE Transactions On Antennas And Propagation, 2006,54(4)∶1292-1304.

[8] 潘越, 杨坤德, 马远良. 粗糙海面对微波蒸发波导超视距传播影响研究[J]. 计算机仿真, 2008,25(5)∶ 324-328.

[9] 刘勇, 周新力, 金慧琴, 等. 粗糙海面对电波传播的影响研究[J]. 电磁场与微波, 2012,42(3)∶38-46.

[10] 刘成国, 潘中伟. 中国低空大气波导的极限频率和穿透角[J]. 通信学报, 1998,19(10)∶90-95.

[11] 蔺发军, 刘成国, 成思, 等. 海上大气波导的统计分析[J]. 电波科学学报, 2005,20(1)∶64-68.

[12] MILLER A R, BROWN R M, VEGH E. New derivation for the rough surface reflection coefficient and for the distribution of sea-wave elevations[C]// IEEE Proc.. 1984∶131, 114-116.

[13] 姚展予, 赵伯林, 李万彪, 等. 大气波导特征分析及其对电磁波传播的影响[J]. 气象学报, 2009,58(5)∶ 605-616.

[14] 陈明逵, 凌永祥. 计算方法教程∶ 工程类[M]. 西安∶ 西安交通大学出版社, 1992∶107-118.