用于非线性有源天线的耦合锁相环特性分析

凌 祥，姜志森，卞 勇

（1．海军装备研究院，上海 200436；2．海军航空工程学院电子信息工程系，山东 烟台 264001；

3．91980 部队，山东 烟台 264001）

微波有源集成天线将有源电路与天线单元直接集成，因而具有体积小、重量轻、成本低、结构紧凑等优点，在移动通信、相控阵和空间功率合成等领域有着广泛的应用前景。为了实现空间波束扫描，近年来许多学者利用非线性动力学的方法研究这种有源集成天线阵列，并且设计了实验系统[1-3]。

有源集成天线阵有多种实现方法，其中包括：单边耦合振荡器阵列、双边耦合振荡器阵列和耦合锁相环阵列。由于耦合振荡器阵列每个单元之间的细小差别会对整个阵列产生很大的影响，使得振荡器单元之间的耦合强度和耦合相位很难精确控制，而且其阵列的锁定带宽很小，大大影响了耦合振荡器阵列的调制性能。由于这些原因，Buckwalter 和Chang 等提出了利用耦合锁相环阵列(Coupled PLL Arrays)来实现无移相器电扫描的另一种新方法[4-5]，这种方法的锁定带宽比耦合振荡器阵列宽得多。但耦合锁相环阵列结构比较复杂，电路延时会对阵列产生很大影响。本文从耦合锁相环阵列的基本单元—互耦PLL 入手，对其稳定性和电路延时性能进行详细分析，并利用一个4 单元阵列对理论分析进行了实验验证。

1 互耦锁相环基本结构

互耦PLL 的基本结构如图1 所示，振荡器1 和振荡器2 的输出信号送给鉴相器，鉴相器的输出信号经低通滤波后分别送给2 个振荡器的谐振电压控制端，调节振荡器的频率，以实现振荡器之间的同步，k1和k2为振荡器自由谐振频率控制端。

图1 互耦PLL 基本结构框图

为简单起见假设2 个锁相环的电路特性是一致的，其相位动力学方程可表示如下：

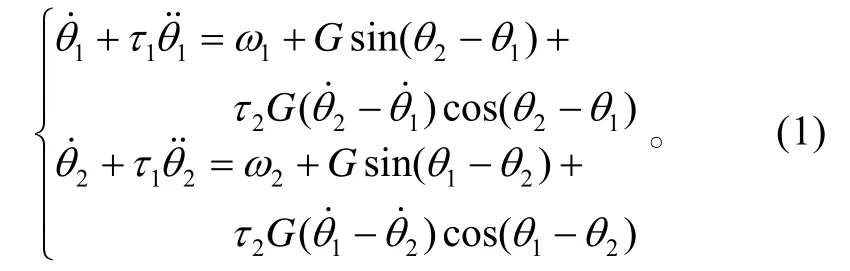
式(1)中：θ1和θ2分别为2 个振荡器输出信号的瞬时相位；G表示锁相环路的直流总增益(振荡器压控灵敏度a、鉴相器的增益b和滤波器直流增益c三者的乘积)；τ1、τ2为低通滤波器的极点和零点。

我们考虑的是系统稳定时的相位差和初始自由谐振频率间的关系，故定义Δθ=θ2−θ1，Δω=ω2−ω1，改写式(1)可得关于相位差的动力学方程[4]：

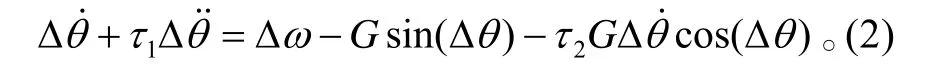
由式(3)得到该方程的平衡点为：

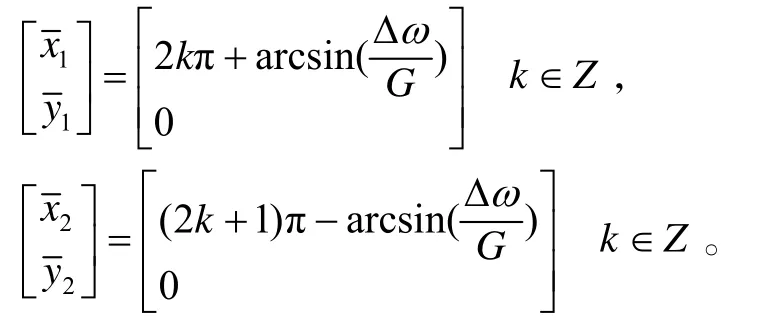
2 系统稳定性分析

由上面的推导可知方程存在多个平衡点，系统的运动状态决定于平衡点的稳定性。可知方程(3)在平衡点的Jacobian 矩阵为

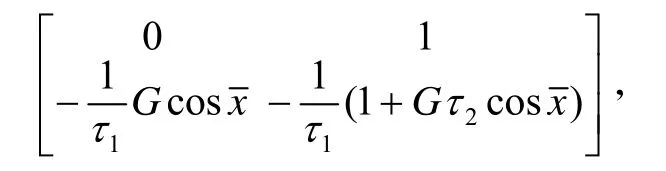
其特征值方程为

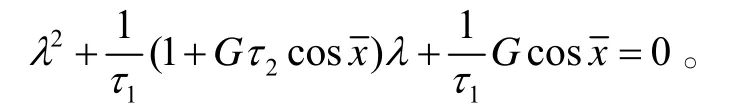
利用罗斯—霍维兹判据可知：

3 耦合PLL 延时性能分析

在耦合锁相环阵列中，时间延迟是不可避免的，主要是由反馈回路造成的[6]，带延时的耦合PLL 阵列的结构如图2 所示。

图2 带延时的耦合PLL 阵列结构图

图2 与图1 不同的是在低通滤波器的后面增加了延时T，由于延时环节的加入，整个系统又表示出不同的非线性动力学特性。

3.1 具有延时的互耦锁相环电路模型

考虑到耦合反馈回路的延时T，将式(2)改写可得到具有延时的耦合锁相环的数学模型：

式中，Td为延时参数。

将上式进行改写，得到：

由于出现了无穷阶导数，使得延时方程实质上成为了无限维系统，方程的解与无延时方程的解相比更复杂，且具有不确定性[7]。

3.2 电路延迟T 对互耦锁相环性能的影响

对于一个确定的反馈回路，其锁相带宽Δω和低通滤波器都是确定的，这些参数与延时参数Td关联性较小。因此，为简单起见，首先确定Δω=10，，然后以延时Td为参数，分析延时动力学方程(4)，由上面的分析可知，无延时的互耦锁相环方程是有稳定定点的，那么当时，锁相环仍能互相锁定，并且是稳定的。以进行仿真，得到Δθ的状态图和的相平面图如图3 所示。

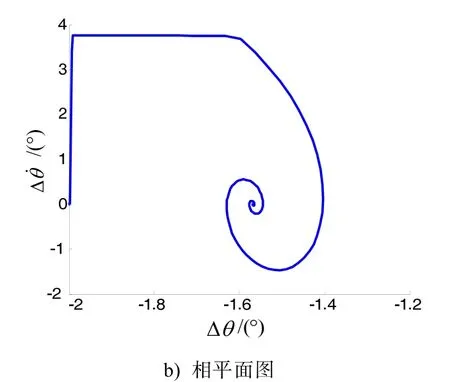
图3 Td=0.1 ns时Δθ 的状态图和相平面图

Δθ为恒定值，表示互耦锁相环达到了同步，并且两者的相位也是确定的，因而相平面上有一个定常吸引子。

图4 Td=0.4 ns 时Δθ 的状态图和相平面图

观察图4 可以发现，Δθ竟然变成了周期性的振荡，而且非常稳定，同时相平面上出现了一个周期吸引子。也就是说，随着延时参数Td的增大，相图发生拓扑结构的突然变化，动力学方程(4)发生了分岔(bifurcation)，并且分析Δθ的频谱可以发现，随着Td的增大，谱线越来越丰富，是一个倍周期的过程。因此，推断继续增大Td，方程(4)可能会出现混沌状态，令Td=0.8 ns 再进行仿真，得到Δθ的状态图和相平面图，如图5 所示。

图5 Td=0.8 ns 时Δθ 的状态图和相平面图

观察Δθ的波形找不到变化规律，类似随机信号，相图也较杂乱，但难以确定方程是否处于混沌运动。混沌具有一个很重要的特性，就是对初始条件的敏感依赖性，也就是说由初值不能确定其真实的运动，由于输入初值的微小差异而导致输出的巨大差别[8-9]。因而改变仿真时VCO 中积分器的初值，2 次初始值分别为1 和0.99，其他条件保持不变，分布进行仿真得到了Δθ随时间变化图，如图6 所示。

图6 初始状态细微差别时Δθ 状态变化图

由图6 与图5 相比可以看到，在刚开始运动时，2 者的曲线还有一段是重合的，但随着时间的演变，2 条曲线完全分离，差别越来越大，并且看不到变化的规律，因而我们可以认为这时方程(4)处于混沌运动状态。

改变TD参数对方程进行全面仿真，得到了方程(4)各分岔点的参数值，随着TD的逐渐增加，开始由定态解失稳进入周期振荡，再经过倍周期分岔进入混沌。

4 实验测试结果

为了验证理论分析的正确性，构建了一个4 单元的耦合锁相环实验阵列，如图7 所示。每个锁相环单元包括集成振荡器、放大器ERA-5XSM、混频器 HMC316、中频放大器 CLC449 和运算器CLC552[4]，实验阵列的原理如图8 所示，图中只画出了2 个单元。

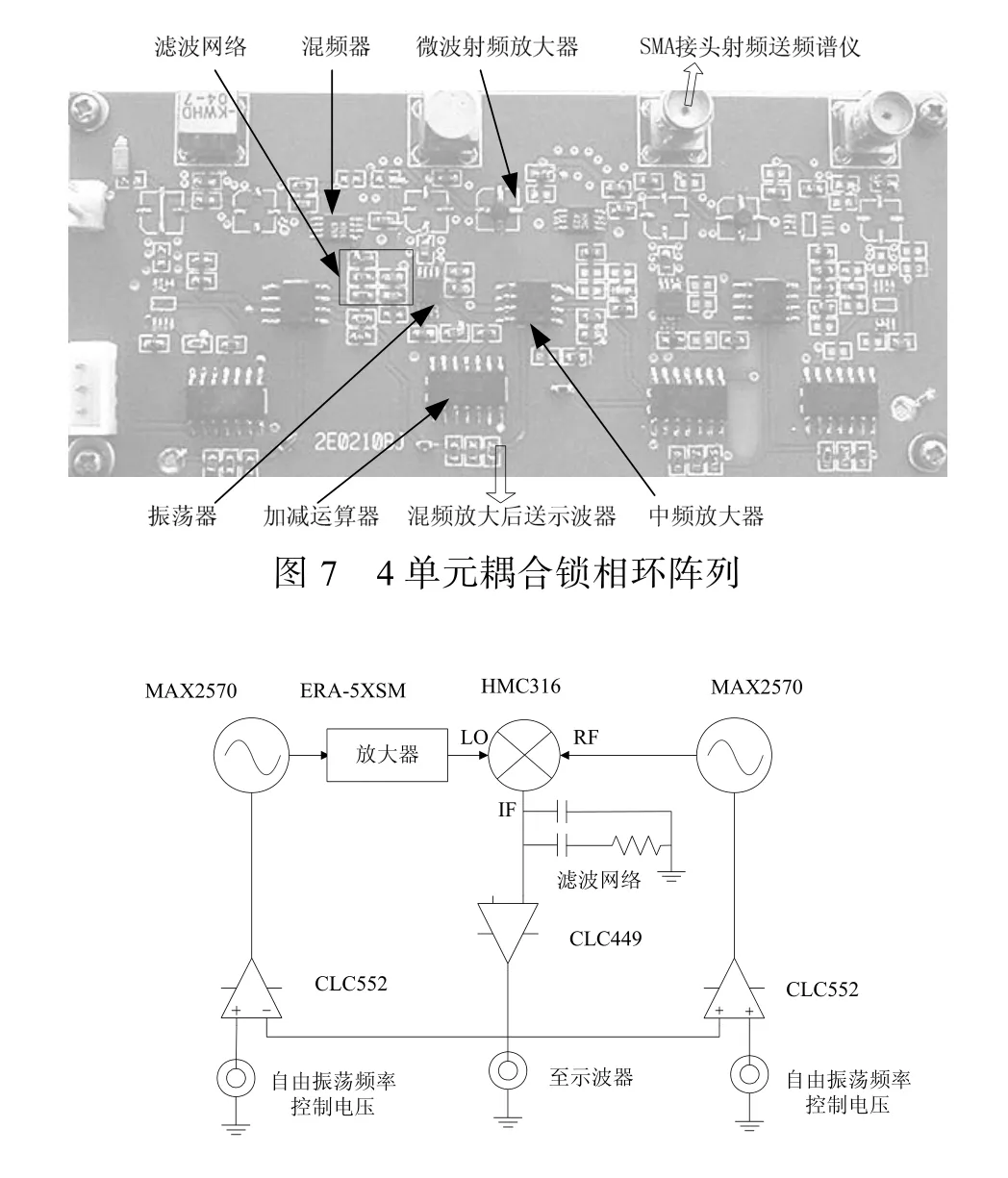
图8 实验阵列原理图

阵列工作在2.4 GHz 左右，VCO 的输出分为2路，一路输出到SMA 接头用于直接观察或送到天线单元发射，另2 路送到混频器与相邻单元的输出进行混频。混频得到的中频信号先进行滤波，再由宽带运放CLC449 放大，然后与自由振荡频率控制电压进行加减，加减的运算由CLC552 来完成。

首先使回路延时为最小，调节VCO 振荡器频率使振荡器频率相互锁定，此时信号频谱如图9 所示。将经过运放后的中频信号进行延时，逐步增大延时量，发现电路失锁，频谱由单根谱线变成了多条谱线，再变成一簇频谱，如图10 所示，而混频器的输出也变得杂乱，如图11 所示。这说明环路的延时对阵列稳定性有很大的影响，也验证了我们在前面的理论分析。

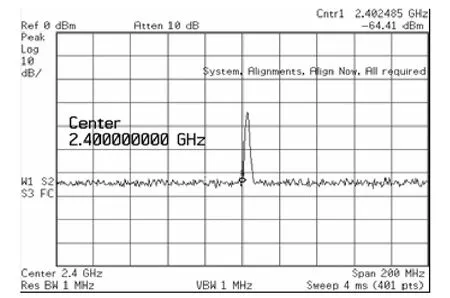
图9 阵列锁定时的频谱

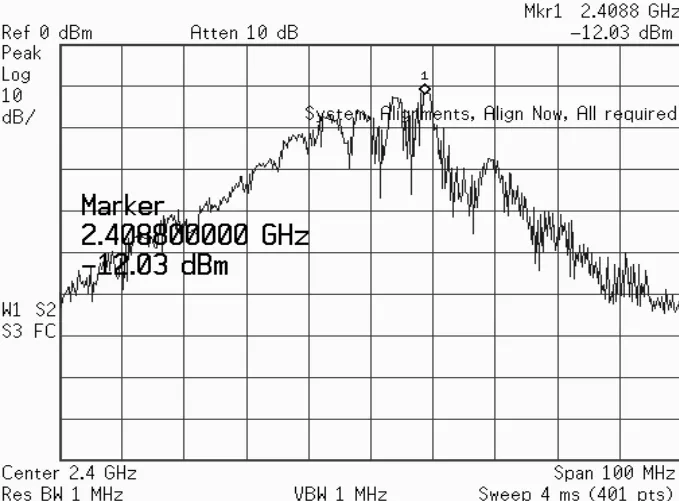
图10 阵列延时增大后的输出频谱

图11 阵列延时增大后相邻振荡器混频输出信号波形

5 结论

耦合锁相环阵列作为一种新型的非线性振荡器阵列，在有源集成天线领域具有很好的应用前景。本文对互耦锁相环单元的稳定性和电路延时对阵列性能的影响进行了理论分析，并作了实验验证。耦合锁相环阵列环路的延时较大，有可能会使阵列失锁。从非线性动力学上来看，随着延时的增加，整个系统也会表现出各种不同的动力学特性，因而在设计时应考虑环路的延时，以提高系统稳定性。

[1] 唐志凯, 刘隆和. 有源天线阵波束电扫描新技术[J].微波学报, 2005,21(4)∶43-46.

[2] 褚庆昕, 艾宝强, 雷振亚. 有源集成天线阵的功率合成和波束扫描[J]. 电子学报, 2005,33(11)∶1952-1954.

[3] KAI CHANG, ROBERT A YORK, PETER S HALL, et al. Active integrated antennas[J]. IEEE Transactions on Microwave Theory and Techniques, 2002,50(3)∶937- 944.

[4] JAMES F BUCKWALTER, TED H HEATH, ROBERT A YORK. Synchronization design of a coupled phase- locked loop[J]. IEEE Trans. Microwave Theory Tech., 2003∶51(3)∶952-960.

[5] HENG CHIA CHANG, ROBERT A YORK. Enhanced MESFET VCO injection-locking bandwidth using low frequency feedback techniques[C]//IEEE MTT-S Digest. 1996∶1515-1518.

[6] JAMES BUCKWALTER, ROBERT A YORK. Time delay considerations in high-frequency phase-locked loops[C]//2002 IEEE Radio Frequency Integrated Circuits Symposium. 2002∶181-184.

[7] 刘秉正, 彭建华. 非线性动力学[M]. 北京∶ 高等教育出版社, 2005∶6-8; 120-143; 135-147; 151-153.

[8] 黄润生, 黄浩. 混沌及其应用[M]. 武汉∶ 武汉大学出版社, 2005∶65-75; 118-134.

[9] RAJEEV J RAM, RALPH SPORER, HANS-RICHARD BLANK, et al. Chaotic dynamics in coupled microwave oscillators[J]. IEEE Transactions on Microwave Theory and Techniques, 2000∶48(11)∶1909-1916.