舰船磁场模型适用范围研究

吕俊伟，于振涛，樊利恒，盖俊峰

（海军航空工程学院控制工程系，山东 烟台 264001）

在进行舰船的磁性防护、水雷的磁引信设计、电磁扫雷具设计、磁性目标的探测定位等过程中，都需要了解磁性目标在整个空间的磁场分布情况，这就要求首先要建立起磁性目标的磁场数学模型。经过近几十年的发展，目前有多种有效的磁场数学模型，其中可用于磁性目标探测定位的模型主要有磁偶极子模型和椭球体模型[1-3]。

磁偶极子模型与椭球体模型相比，数学表达简洁，容易进行各种数学运算，因而基于磁偶极子模型的定位算法较多，且这些算法的运算量较小，能够快速实现磁性目标的探测定位，所以在舰船磁性目标的探测定位中，目前应用最为广泛的是磁偶极子模型[3-5]。但对于磁偶极子模型适用的观测距离(即磁力仪测量点到磁性目标的距离)，目前的研究只有定性的结论，即磁偶极子模型只适用于表达磁性目标的远程磁场，对于近程磁场的表达存在较大误差。而随着磁偶极子模型在磁性目标定位算法中的广泛应用，需要量化磁偶极子模型适用的观测距离。

椭球体模型将舰船磁性目标视为一个均匀磁化的旋转椭球体，其精度大大优于磁偶极子模型，尤其是近程磁场的表达，椭球体模型可以近似表达实际磁场[6-8]。本文利用磁偶极子模型和椭球体模型，分别对舰船磁性目标的空间磁场分布进行了仿真计算，并通过比较分析量化了磁偶极子模型的适用观测距离。

1 舰船磁场模型

建立舰船磁性目标的空间磁场模型是探测定位舰船磁性目标的基础。目前应用最为广泛的是磁偶极子模型，航空探测潜艇的一些算法和磁梯度张量探测算法都是在磁偶极子模型的基础上建立的。椭球体模型建模的精度高，但未知参数多，计算量大，当观测点数量能够满足需要时，可以采用椭球体模型，通过解决非线性最优化问题，实现舰船磁性目标的定位。

1.1 磁偶极子模型

磁偶极子模型将舰船磁性目标视为一个磁偶极子，距离磁性目标r处的磁场强度可以表示为[9-10]

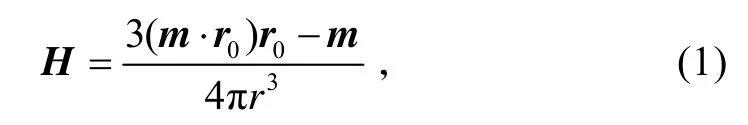
式中：m为水中磁性目标的磁矩；为磁性目标到测量点的距离；r0=r/r为沿r的单位矢量。

1.2 椭球体模型

椭球体模型的建模方法，将舰船视为一个均匀磁化旋转椭球体。舰船的实体坐标系如图1 所示。将舰船的x轴作为椭球体的长轴，y轴与z轴为短轴，椭球体长半轴a为船长L的一半，其短半轴b通常取为船宽B的一半，半焦距，模型结构如图2 所示。

图1 舰船的实体坐标系

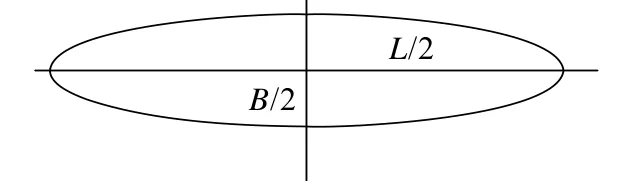
图2 旋转椭球模型

设舰船在P(x,y,z)处所产生的磁场 3 分量为Hx、Hy、Hz，则有[6-7]：

式(2)中：Mx、My、Mz分别为旋转椭球体沿x轴、y轴、z轴方向的磁矩分量。式中各系数的表达式为：

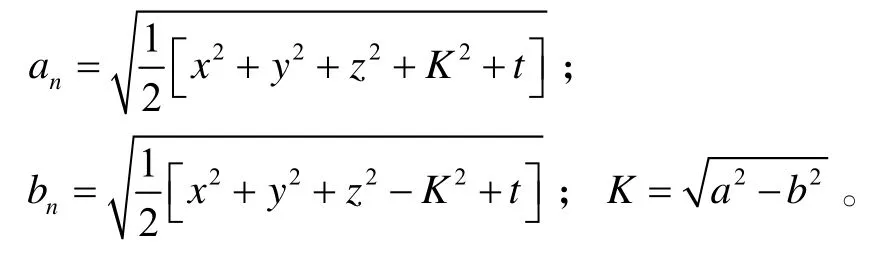
2 仿真分析

分别采用磁偶极子模型和椭球体模型对3 个船模的空间磁场进行仿真表达，3 个船模的选取分别代表小型、中型和大型舰船，椭球体模型表达的磁场作为近似实际磁场。仿真计算采用图1 所示的舰船实体坐标系。

船模一的参数：舰船长度L=47 m，舰船宽度B=10 m，舰船的磁矩Mx=2.5×105A·m2、My=0、Mz=0。船模二的参数：舰船长度L=75 m，舰船宽度B=8.3 m，舰船的磁矩Mx=1×106A·m2、My=0、Mz=0。船模三的参数：舰船长度L=120 m，舰船宽度B=10 m，舰船的磁矩Mx=4×106A·m2、My=0、Mz=0。船模一、船模二和船模三空间磁场的仿真结果见表1～3。

由仿真结果可知，磁偶极子模型仿真表达的空间磁场和椭球体模型近似仿真表达的实际磁场，在近场时2 者的差别较大，随着距离的增大2 者的差别变小。分析可知，磁偶极子模型的适用观测距离与磁力仪传感器的精度有关，即当磁偶极子模型的相对误差小于磁力仪精度时，磁偶极子模型可用。因此，分析以上仿真结果，可以得出如表4 所示的结论。表4 分别给出了3 个船模磁偶极子模型的适用观测距离临界值，当磁力仪观测点到舰船磁性目标的距离大于这个临界值时，可以使用磁偶极子模型以及相关算法。

表1 船模一的空间磁场仿真及磁偶极子模型误差

表2 船模二的空间磁场仿真及磁偶极子模型误差

表4 磁偶极子模型的适用观测距离

3 总结

本文利用椭球体模型近似表达舰船磁性目标的实际磁场，并通过对3 个船模磁偶极子模型和近似实际磁场的仿真比较分析，得出了磁偶极子模型用于探测舰船目标的适用观测距离。结论对探测舰船磁性目标的磁场模型选取有一定的参考价值，但本文的研究还存在2 点不足：

①虽然椭球体模型的精度较高，但是与实际磁场相比仍存在误差，因而本文的结论也存在一定误差；

②本文选取了3 个船模，分别代表小型、中型和大型舰船，但现实中的舰船多种多样，只讨论这3 种还远远不够。在下一步的研究工作中，需要利用各种舰船的实际测量数据对本文的结论进行验证。

[1] 翁行泰, 曹梅芬. 磁异探潜中潜艇的数学模型[J]. 上海交通大学学报, 1995,29(3)∶27-32.

[2] TAKAAKI NARA, SATOSHI SUZUKI, SHIGERU ANDO. A closed form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients[J]. IEEE Transactions on Magnetics, 2006,42(10)∶3 291-3 293.

[3] 唐劲飞, 龚沈光, 王金根. 基于磁偶极子模型的目标定位和参数估计[J]. 电子学报, 2002,30(4)∶614-616.

[4] 张朝阳, 肖昌汉, 阎辉. 磁性目标的单点磁梯度张量定位方法[J]. 探测与控制学报, 2009,31(4)∶44-48.

[5] 张昌达. 航空磁力梯度张量测量—航空磁测技术的最新进展[J]. 工程地球物理学报, 2006,3(5)∶354-361.

[6] 林春生. 舰船磁场信号检测与磁性目标定位[D]. 武汉∶ 海军工程大学, 1996.

[7] 边新迎, 李庆民, 李华. 舰船实时磁定位方法研究[J]. 探测与控制学报, 2006,28(5)∶35-38.

[8] 李华, 李庆民, 刘君. 两种舰船磁场模型结构的比较研究[J]. 探测与控制学报, 2007,29(8)∶62-66.

[9] 叶平贤, 龚沈光. 舰船物理场[M]. 北京∶ 兵器工业出版社, 1992∶53-62.

[10] 谢处方, 饶克谨. 电磁场与电磁波[M]. 北京∶ 人民教育出版社, 1979∶63-70.