一种应用于弹道导弹控制的朗伯特导引方法

高 勇

（海军驻航天科技集团公司第一研究院军事代表室，北京 100076）

与大气层内使用升力进行操纵的战术拦截器不同，大气层外拦截器需要使用推力矢量装置以响应制导命令。如果所有用以转向的燃料已经耗尽，拦截器就不再可操纵了。也就是说，燃料是一种超量，因为根据火箭方程，拦截器的重量按燃料重量的指数倍增长。因此，与大气层内战术导弹不同，大气层外拦截器需要消耗燃料最少的制导规律。本文中采用的导引方法，能够用于将一枚拦截弹发射到与弹道目标导弹相同的弹道轨迹上，通过改变拦截弹的飞行时间，可以使完成弹道飞行所消耗的额外燃料最少[1-2]。

由椭圆轨道朗伯特飞行时间定理可知：设1点和2点为空间两个任意的固定点，它们的向径分别为r1和r2，若r1+r2=常数，椭圆半长轴a=常数，1点和2点之间的距离c=常数，则从1点至2点的飞行时间Δt也是固定的。朗伯特导引用于计算在预定的飞行时间内以弹道方式从位置1运行到位置2所需要的速度，该方法已广泛应用于控制主动段内的导弹，在预定时间击中射向范围内的目标点[3]。然而，朗伯特导引仅能用于将拦截弹导引到与目标导弹相撞的轨道，而不能控制拦截弹到达目标导弹时的末段速度。如果拦截弹的速度矢量与目标导弹的速度矢量不一致，两枚导弹将在到达最接近的位置后相互分离。如果用某种导引方法使拦截弹在与目标导弹最接近的位置时具有相同的速度矢量，那么两枚导弹将从该点开始以相同的弹道轨迹飞行。

利用动力系统的剩余能量，可以使经典朗伯特导引方法得到拓展，从而实现匹配弹道目标位置和速度的目的，一旦位置和速度相一致，拦截弹就将跟随弹道目标飞行。应用迭代方法可以使拦截弹与弹道目标之间的速度差Δv最小，如果把弹道目标的速度表示为时间的函数并且存在闭合解，则可求得解析解。拦截弹发动机关机时的速度和弹道倾角可被设定成用于生成一个椭圆轨道，在到达弹道目标时，使它的速度在特定时刻唯一最小化。使用开普勒飞行时间方程可以解决到达未来某一位置的飞行时间问题，通用的飞行时间方程必须通过迭代方法求解，其结果代入开普勒常数以计算未来某一时刻t的速度。有很多参考资料描述了环绕地球运行的人造卫星的优化会合轨道问题，它们都是以轨道卫星的平面变换问题为基础的。通常，这种平面变换中的Δv机动(其结果对轨道有影响)可以超过一个或多个轨道周期(100 min或更多)。弹道导弹与轨道卫星相比，飞行时间较短，在与弹道目标碰撞之前，Δv机动必须经历一段几十秒到几百秒的周期来到达有效会合点。

1 朗伯特导引

朗伯特问题涉及物体在牛顿引力场中的运动规律，其解决方案给出了在仅受重力的情况下，物体在特定时间内从初始位置rl运动到最终位置r2所需要的瞬时速度。假设在大气层内飞行的主动段导弹(受推力、气动力和重力作用)，在每一个积分步内都要解决朗伯特问题，需要速度(朗伯特速度)vL减去当前导弹实际速度vM即得到待增速度vG，如图1所示。待增速度的物理含义是：由导弹的当前状态(r，v）给其瞬时增加速度增量vG，而后导弹依惯性飞行便可命中目标，因而将vG称为待增速度。在低大气层中，导弹以一个固定的弹道倾角飞行，这样可以减小大气阻力的损耗。导弹沿vG加速，当vG达到某一限定范围时，导弹的推力中止，导弹以弹道方式飞向预定目标[4]。

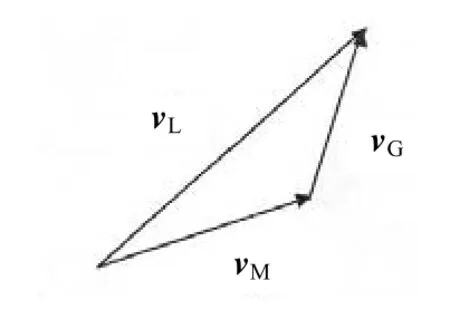
图1 朗伯特导引速度矢量图

初始位置矢量rl和终点位置矢量r2如图2所示，rl为拦截弹的瞬时位置矢量，r2为与弹道目标的预定会合点位置矢量。θf是由飞行方向确定的角度，可由公式表达为：

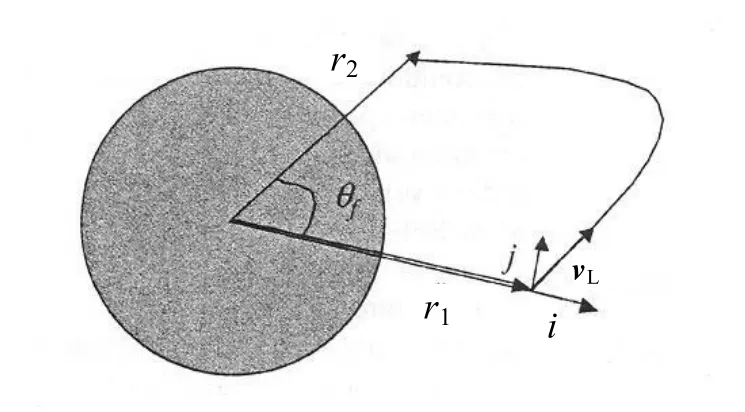
图2 含初始位置矢量和终点位置矢量的朗伯特平面图

文中使用的所有弹道的延伸范围均小于地球圆周的一半(即θf＜180°)。对于角度大于180°的情况，则不存在速度作为时间函数的闭合解。朗伯特导引解算过程为，速度可通过迭代法求得，弹道倾角γ可选定，速度v和飞行时间tf的计算方法如下[1]。

a) 选择弹道倾角γ。

b) 按公式(2)、(3)计算v、tf：

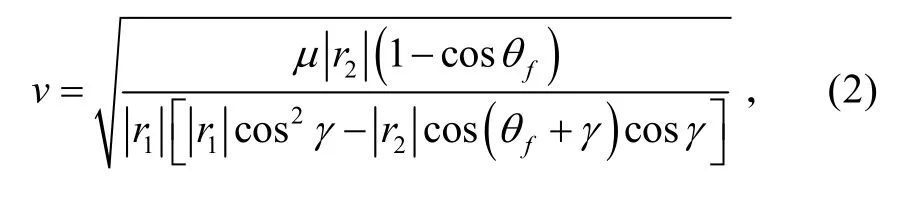
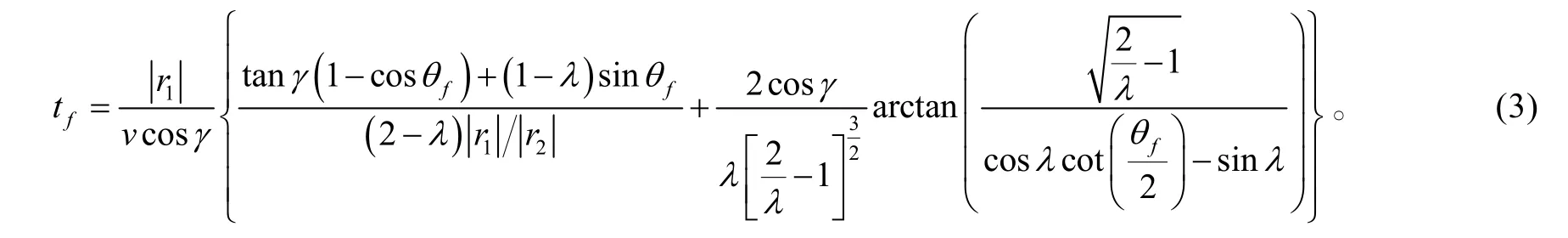
c) 如果tf＞理想值，则弹道较高，应减小γ，执行e)步。

d) 如果tf＜理想值，则弹道较低，应增大γ，执行e)步。

e) 重新选择弹道倾角γ，继续上述计算，直到tf收敛到理想值。

由二维平面弹道结构变换为三维地心惯性仿真计算结构的朗伯特方法参见图2和上述计算，vL表示在地心惯性坐标系中的朗伯特速度矢量，导弹沿vG矢量运动，使vM和vL趋近于一条直线，仿真交汇在目标耗尽燃料之后开始进行，此时目标位于可见大气层之上的某一海拔高度。在再入之前的任一时刻，目标在引力场中的位置可用其耗尽关机时刻的状态矢量信息推算出来。在仿真中，拦截弹飞向计算好的会合时刻的目标点，其关机时刻的状态矢量取决于输入的目标弹道。也可以使用同一导引方法，在沿目标弹道的多个位置进行拦截仿真，从而使导弹拦截器的方案和结构设计达到最优。

2 匹配目标速度的末修机动

仿真应用朗伯特导引方法使拦截弹在三维空间中到达与弹道目标相同的位置，然而，当导弹到达目标点时，朗伯特导引没有直接控制导弹的速度，如果导弹速度矢量不改变，导弹在到达目标后将不能以相同的弹道轨迹跟随目标运动。为了与目标相匹配，可以设计一个短暂的末修段，用来改变导弹的速度矢量。推力矢量P(沿矢量Δv)用于改变导弹的速度矢量，推力矢量P的x、y、z分量与Δv矢量的各分量方向一致：，这里，

推力大小等于比冲Is乘以推进剂燃烧速率，因为末修机动在外大气层进行，所以阻力可以忽略不计。末修级启动时的初始质量为W4，当火箭发动机工作时，质量开始消耗，末修级沿矢量Δv的运动方程为[7]：

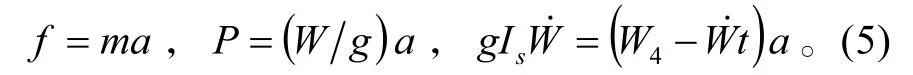
重力引起的加速度可以忽略不计，因为拦截弹和弹道目标都处于同一个重力场，重力比火箭发动机的推力要小，该公式用于计算为减小拦截弹与弹道目标之间的Δv而消耗的发动机工作时间，Δv只是一个相对速度，不是一个绝对速度。这个公式可以解释为，由末修级发动机工作产生的加速度：

加速度对时间积分就可以得到速度：

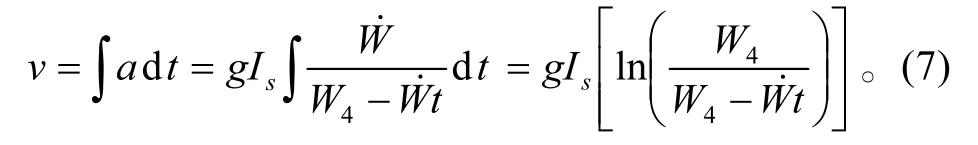
公式(7)是一个标准火箭方程的形式，以下表示的是速度公式，将发动机燃烧时间ΔT表示为必须达到的速度变化Δv的函数：

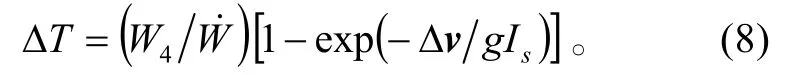
即，导弹仿真的末修段在导弹距目标会合点ΔT时沿Δv矢量开始运行，可是这种短暂的末修段将导致导弹无法到达理想的目标点，这是因为末修段将导弹推离了弹道目标点，为了补偿这种误差，朗伯特导引将引导导弹到达新点为预定的弹道目标点，ΔR为由末修段引起的脱靶距离，如图3所示。

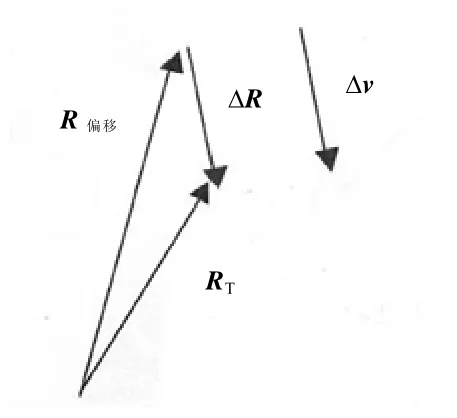
图3 由末修段引起的位置偏移

用推导的方程计算需要由末修段调节的位置偏移量ΔR，方程(7)为速度方程，可每秒积分一次，从而得到由末修引起的运动距离，下列方程表示末修运动距离作为发动机工作时间的函数：

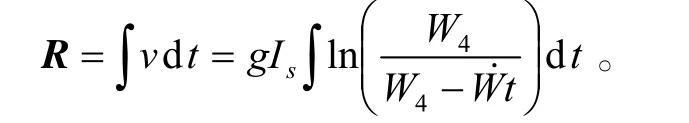
∵0→t为Δt，则为ΔR，

ΔR矢量的x、y、z分量与ΔV矢量的各分量方向一致，如下列方程和图3所示：

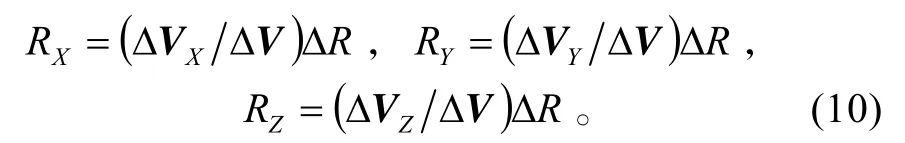
最终的仿真程序运行是在主动段时使用朗伯特导引将导弹导引至一点，该点与弹道目标点偏移ΔR，当拦截时刻到达ΔT时，短暂的末修段开始，导弹沿着与目标相同的弹道轨迹以需要速度飞向弹道目标。

3 用拦截弹飞行时间使拦截弹与弹道目标之间的速度差最小化

拦截弹在弹道目标射向上的某一点发射，导弹飞向目标的弹道形状由2个参数确定：导弹到达弹道目标的时刻TA和导弹发射时刻TD，2个时间都与弹道目标的关机时刻有关[8]。

在发射延迟时间较短时，朗伯特导引将产生高弧线弹道以大倾角与目标弹道相交；在发射延迟时间较长时，朗伯特导引将产生低弧线弹道，以更合适的角度与目标弹道相交。为匹配弹道目标的速度，需要改变拦截弹的速度，从而产生Δv，该矢量的量级与拦截弹弹道与弹道目标弹道相交的角度有直接关系。在这种情况下，低弧线弹道将导致Δv较小，较小的Δv是希望的，因为这将减少需要执行末修段以匹配弹道目标速度所消耗的推进剂，通过减小末修级推进剂的重量，就可以减小整个导弹的重量。

弹道目标到达时间与导弹发射延迟时间的优化组合，可以使导弹与弹道目标速度之差Δv达到最小。Δv是弹道目标到达时间与导弹发射延迟时间的函数，该结论由10 164次不同的仿真运算得出，其中加入了84次不同的到达时间(1 000～1 400 s)和121次不同的发射延迟时间(100～500 s)的运算组合。这是一个简单的由两个输入条件确定的Δv最小化问题，在多维状态下用于确定TA与TD的最佳组合，得到最小的Δv。

通过仿真可知，对一个特定的导弹发射点而言，可以使Δv最小，下一步就要看最优的拦截发射延迟在不同的射向和侧向发射点上如何变化。通过改变与弹道目标弹道相关的拦截弹射向和侧向上的发射点，计算每一个发射点的最优飞行时间Tf，所有的拦截弹仿真都与弹道目标会合于同一点，即TA=1 400 s 。最佳导弹发射延迟时间TD作为拦截弹发射位置的函数，发射延迟时间TD=1 000 s ，相应的飞行时间Tf=400 s ；发射延迟时间TD=200 s ，相应的飞行时间Tf=1 200 s 。最佳发射延迟时间为：在拦截弹发射点与目标发射点相距较近时，拦截弹发射延迟时间较短；在拦截弹发射点与目标发射点相距较远时，拦截弹发射延迟时间较长。侧偏对最优发射延迟是有影响的，当拦截弹发射点沿目标弹道有侧偏时，最优拦截弹发射延迟时间将减小。

4 通过迭代消除由重力影响引起的脱靶距离

通过朗伯特导引，第一步仿真使导弹到达目标点RT，然后计算在最近的到达点时导弹与目标间的Δv，再计算ΔR，进而调整末修段来修正Δv偏差。第二步仿真将导弹导引至偏移R并执行末修段以达到与目标相同的位置和速度。然而，导弹的速度还没有精确地匹配目标的速度，这是因为导弹在第二步仿真导引至偏移R时的运行轨迹与第一步仿真导引至RT时的运行轨迹有微小差异，这种位置上的变化导致最终速度的微小误差，该误差是由导弹在飞行过程中的位置变化引起的重力差异而产生的。重力梯度对较短的工作周期，即末修段影响很小，但是，重力梯度对从关机到拦截这种较长的预定间隔的影响并不小，这些差异需要瞄准点策略的迭代计算。为了补偿这些误差，直到仿真运算达到收敛，Δv才会很精确。过程如下：计算Δv，再运行导引至偏移R，并重复计算直到连续迭代不能改变Δv。通常仅需2～3次迭代，Δv即达到快速收敛。

仿真运算表明，导弹在TA时刻到达目标点，然后迅速飞离，这是因为目标与导弹间的速度差异较大。使用末修级Δv机动后的第1次迭代运算表明，导弹在TA时刻到达了目标点，但随后慢慢飞离，这是因为，在重力的综合影响下产生了微小的速度差异。Δv的第2次迭代运算表明，导弹在TA时刻到达目标点，且与目标速度一致，有了这些匹配条件，导弹在随后的弹道飞行中将跟随目标运动。

5 最终结果

导弹三自由度仿真用于生成弹道和速度曲线图，从而在特定到达时刻与弹道目标的位置和速度相匹配。图4表示3个导弹的飞行弹道，这3条弹道都在预定时刻TA到达弹道目标。弹道A用一个简单的朗伯特导引到达目标点，但是没有末修机动以匹配目标速度，弹道A在到达时刻后迅速与弹道目标弹道分离；弹道B用朗伯特导引到达目标，并做末修机动以匹配目标速度，弹道B有一个短暂的延迟时间并以一个大倾角的高弧线弹道到达目标弹道。结果，末修级的Δv较大；弹道C在优化延迟时刻发射，导弹沿低弧线弹道以合适的角度到达弹道目标弹道。结果，Δv比弹道B小很多。因为弹道C以一个合适的角度到达弹道目标弹道，它的末修级待增速度Δv与弹道B相比减小了大约40%，待增速度Δv由于低弧线弹道也减小了，弹道B因为高弧线弹道引起潜在的较大能量变化而损失了很多速度。因此，弹道B在匹配弹道目标速度时，需要弥补更多的速度损失[9-11]。

图4 匹配弹道目标的位置和速度的拦截弹弹道

6 结论

本文介绍的是一种改进的朗伯特导引方法，它可以用于匹配弹道目标的位置和速度，而传统的朗伯特导引方法仅可用于匹配目标的位置。通过末修机动可以实现与目标速度的匹配，使拦截弹的飞行时间得到优化，使末修级的待增速度Δv达到最小，末修机动的发动机燃烧速度W˙可被限定在满足其最大加速载荷的量级。仿真结果表明，该导引方法可将末修级导引至跟随弹道目标的轨道上，且对于匹配弹道目标的位置和速度是有效的，迭代运算也足够快，对真实弹道目标可以实时完成解算。将拦截弹导引至与目标导弹相同的弹道轨迹上是可行的，当拦截弹发射点与目标弹道轨迹相比沿侧向和射向距离越远，则末修级的待增速度Δv就相应增加。当拦截弹发射点沿目标发射点的射向移动时，最优的拦截弹发射延迟时间也相应增加。换句话说，当拦截弹发射点沿射向移动时，可以使拦截弹的发射时间推迟，该方法可以用于找到使末修级的待增速度Δv最小的拦截弹飞行时间。

[1] A RICHARD SEEBASS. 战术导弹与战略导弹制导技术(下册)[M]. 华盛顿∶ 美国航空航天学会科学出版社, 1994∶221-282.

[2] 侯世明, 周木波, 田锡惠, 等. 导弹与航天丛书—固体弹道导弹系列∶ 导弹总体与试验[M]. 北京∶ 宇航出版社, 1996∶102-127.

[3] WHITE J E. Guidance and targeting for the strategic target system[J]. Guidance, Control and Dynamics, 1992,15(6)∶1313-1319.

[4] 陈世年, 李连仲, 王京武. 控制系统设计[M]. 北京∶ 宇航出版社, 1996∶192-217.

[5] ZARCHAN P. Tactical and Strategic Missile Guidance, Progress in Astronautics and Aeronautics[M]. Washington, D.C.∶ American Institute of Aeronautics and Astronautics, 1997∶263-289.

[6] NELSON S L, ZARCHAN P. Alternative approach to the solution of lambert’s problem[J]. Guidance, Control and Dynamics, 1992,15(4)∶1003-1009.

[7] 吴文正. 导弹引论[M]. 北京∶ 国防工业出版社, 1990∶27-56.

[8] GUELMAN M. Boost Phase Interception of Ballistic Missiles, in Ballistic Missiles∶ The Threat and The Response[M]. Shaarei Tikva∶ Ariel Center for Policy Research Publisher, 1999∶241-249.

[9] PRUSSING J E. A class of optimal two-impulse rendezvous using multiple-revolution lambert solutions [J]. Astronautical Sciences, 2000,48(2-3)∶131- 148.

[10] HUMI M. Fuel-optimal rendezvous in a general central force field[J]. Guidance, Control and Dynamics, 1993,16(1)∶215-217.

[11] LEMBECK C A, PRUSSING J E. Optimal impulsive intercept with low-thrust rendezvous return[J]. Guidance. Control and Dynamics, 1993,16(3)∶426-433.