短波信道下基于PSWF的非正弦时域正交信号调制解调实现

孙小东，潘耀宗，2，康家方，李 丹

（1．海军航空工程学院电子信息工程系，山东 烟台 264001；2．92407 部队，河北 秦皇岛 066200； 3．中国联合网络通信有限公司烟台市分公司，山东 烟台 264000）

短波通信是历史悠久、应用广泛的通信方式之一。尽管当前许多新兴的通信技术不断吸引着人们的眼球，但是短波通信凭借着设备轻便、易于架设、使用维护简单、通信距离远、传输无须中介、顽存性强等优点，始终在国家战略通信网中占有一席之地。随着微电子、数字信号处理、自适应等现代信息技术的发展及其在短波通信中的应用，短波通信性能得到了极大改善。在通信技术发展的道路上，短波通信正在向以网络化、数字化为主要技术特征的第三代短波通信迈进[1]。

短波通信虽优势独特，但受到可用频带窄、多径时延、频移等短波信道固有特性的影响[2]。基于椭圆球面波函数(Prelate Spherical Wave Function，PSWF)的非正弦时域正交调制技术，采用多路并行传输，延长了码元的持续时间，增强了对短波信道多径效应的抵抗能力。PSWF 的高能量聚集性，又可以极大地降低对其他频段通信的干扰。并且，频带利用率较OFDM 技术可以更快的接近理论极限值[3]。所以，研究其在短波通信中的应用，对提高短波通信的性能有重要意义。

目前，在短波频段内基于PSWF 的非正弦时域正交调制解调动态仿真实现、仿真中小相对带宽PSWF 脉冲生成，为原理样机的实现提供先验支撑等方面，还未见文献进行相关报道。本文利用Simulink 软件对基于PSWF 非正弦时域正交信号的调制解调进行了实现，并在短波频段内进行了性能仿真，对得到的仿真结果进行了分析。这对研究非正弦时域正交调制信号在短波信道内的特性和原理样机的实现有重要意义。

1 短波信道仿真模型分析

1.1 短波信道仿真模型的主要类型

短波信道仿真模型主要有2 大类：基于统计的仿真模型和基于探测信号记录的重放仿真模型。

1)基于统计的仿真模型可以进行若干固定条件(多径、多普勒条件等)下的仿真。可以分为窄带信道仿真模型和宽带信道仿真模型。适用带宽小于12 kHz 的模型称为窄带信道仿真模型，适用带宽大于12 kHz 的模型则是宽带信道仿真模型。Watterson模型是传统窄带信道模型中的标准模型，自1969年被Watterson 等人提出后，该模型得到广泛接受，并被CCIR 推荐。宽带信道模型中最具代表性的是上世纪90年代提出的ITS 模型。它主要是针对Waterrson 模型不能准确反映高纬度地区和近赤道地区电离层特性的局限性而提出的。尽管ITS 模型是作为宽带模型被提出的，但它适用于窄带和宽带2 种情况。

2)基于探测信号记录的重放仿真模型是利用具有代表性的探测记录完成对短波信道仿真。信道仿真过程见图1。第一步是通过发送短波频段内的探测信号完成信号探测记录，并记录信道噪声。(图中虚线外的部分)；第二步是通过探测信号记录，提取信道的冲激响应，经过滤波进一步减小其噪声，最后和仿真信号进行卷积，并且叠加记录的噪声，得到经过短波仿真信道的信号(图中虚线内的部分)[1]。进行仿真的时候要选用具有代表性的探测结果。

图1 重放仿真模型

由于实验条件的限制，本文采用的是基于统计的短波信道仿真模型。由于研究的对象是3 kHz 带宽的短波信号，所以采用的是窄带信道仿真模型。考虑到ITS 模型的复杂度较高，本文最终选用窄带短波信道仿真模型中的代表：Watterson 短波信道仿真模型。

1.2 Watterson 短波信道模型原理

Watterson 模型将短波信道看作由带抽头的理想延迟线构成，每个抽头系数对信号进行调制，从而使信号发生多普勒频移、衰减等，最后各抽头上的信号叠加，并混入高斯白噪声。具体流程如图2所示。

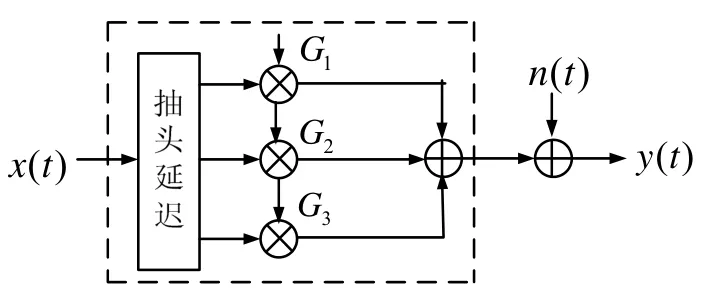
图2 Watterson 短波信道模型原理图

输入信号x(t) 在各个路径上经过不同的时延，在抽头系数的作用下发生了多普勒频移、衰减等各路叠加后被加入高斯白噪声n(t) ，最后形成经过仿真信道的信号y(t) 。图2 中虚线内的部分，可用信道冲击响应h(t) 表示。

式中：N表示一共有N条传输路径，τl(t)表示第l条路径上t时刻的相对时延，al(t)表示第l条路径上t时刻相对于主径的幅值，fl(t)表示第l条路径上t时刻的频移。虽然，短波信道是时变的，但是在有限的时间和带宽下，信道特性可以保持平稳[4]。为方便分析，假设频移、相对时延和各路的相对幅值，都是静态的。h(t) 被简化为

式中：N取值2～4 的约占85%[5]；lτ取值0.5～5 ms的约占99%[6]；lf取值大约在1～2 Hz[1]。此为仿真分析的取值范围。

信号x(t) 经过短波信道模型后的y(t) 的表达式为

2 基于PSWF 的短波非正弦时域正交信号生成调制解调原理

2.1 短波频段内PSWF 的生成

目前对PSWF 数值求解有很多算法，可归纳为3 种：第一是利用PSWF 的微分方程定义式，采用Legendre 多项式逼近，通过迭代得到近似解[7-8]。此方法以迭代的计算量换取求解的精度。尽管数值解精度高，但运算量大、效率低。第二是利用采样定理建立PSWF 积分方程定义式与矩阵的对应关系，通过求矩阵的特征向量，求得PSWF 近似数值解[9-10]。此方法可以产生任意波段的椭圆球面波，但是在构建矩阵时，同样存在着计算量大的问题。第三种是基于信号通过带通滤波器的思想，由PSWF的频域积分方程求得其时域积分表达式，离散化后构造Toeplitz 矩阵，最后通过计算其特征向量得到PSWF 的近似解[11]。此方法计算速度快、物理意义明确，但是仅能利用求解信号的离散采样值。

在仿真过程中，考虑到前2 种方法求解效率低，本文采用了第3 种方法，但是，短波频带上产生3 kHz 带宽的PSWF 时，遇到了小相对带宽信号采样率太高，致使仿真软件中Toeplitz 矩阵不能正常运算的问题。故本文采用文献[12]提出的一种PSWF的重构算法。

该算法的基本思想是：首先，依据采样定理得到能够准确恢复该PSWF 信号的最低采样频率；其次，构造并解得Toeplitz 矩阵的特征向量；最后，通过重构表达式得到预求的PSWF 数值解。该方法求解过程中不涉及迭代和积分运算，计算量小、求解效率高，不受采样率限制，易于工程实现。尽管重构过程中，对PSWF 的能量集中度有一定影响，但程度很小，仍可满足工程应用的要求。

求解具体步骤如下：

1)根据待求PSWF 的带宽B0、脉冲持续时间t0、中心频率f0和时间带宽积C确定求解参数。由f0和B0确定B≥B0，使其满足

式中，M为正整数。

由带通采样定理确定采样频率fs≥fN=4B，再由sf及t0确定最低采样点数：

式中，┍┑表示向上取整。由f0和B求得重构函数k(t)的表达式：

2)根据最低采样点数Nmin，计算得到PSWF 的采样值。即：

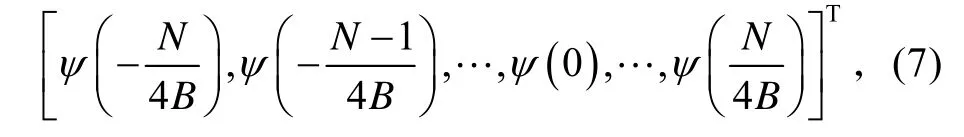
其中，连续的ψ中得到其不同时刻的离散值。

3)将k(t) 和所得PSWF 的采样值代入式(8)便可以得到PSWF 的重构解。

2.2 非正弦时域正交信号调制解调原理

非正弦时域正交信号调制解调的基本思想是，数据流经过串并变换后，各路分别选取PSWF 脉冲集中的一个脉冲进行调制，产生的各路调制信号相加，得到待发射的调制信号。经信道后，在解调端利用PSWF 脉冲的正交性，采用相关解调方式得到各路数据，经并串变换后得到数据流。基本流程如图3 所示。

图3 时域正交信号调制解调流程图

数据流D(t) 串并变换后，分别与进行调制并合成一路经短波信道后，接收信号分别与ϕi(c,t)进行相关运算，通过判决得到每路的传输数据。最后，进行并串变换得到预传输的数据流D(t) 。

3 基于Simulink 的仿真模型建立

在利用Simulink 对短波信道条件下非正弦时域正交信号调制解调进行实现时，共分为：信源和PSWF 脉冲生成、时域正交调制、仿真短波信道、解调、误码率计算等模块。

调制路数为4 时，仿真模型如图4 所示。

图4 仿真系统模型

由随机数生成模块作为信源产生传输数据，串并变换模块后传输数据由一路变为多路，在调制模块用PSWF 脉冲进行调制后叠加，然后经过短波信道仿真模块进行信道仿真，而后在解调模块进行相关解调，经并串变换模块得到接收数据，最后通过误码计算器来计算误码率。

1)信源和PSWF 脉冲生成。利用随机数生成模块，随机等概生成1 和0，作为仿真模型的信源。本文采用2.1 节说明的方法进产生，短波频段内的PSWF 脉冲。

2)串并变换模块。模块结构如图5 所示。由0和1 组成的数据流从端口“In1”进入，经过“Swich”模块后变为对应的由−1 和1 组成的数据流。经过“Buffer”和“MultiportSelector”后，最终数据流由 1路变为了4 路，此时的码元持续时间为串行码元持续时间的4 倍。

图5 串并变换模块

3)调制模块。调制模块的结构如图6 所示。4路并行传输的数据分别经“In1”到“In4”进入调制模块，通过相乘器对存储在“direct sine table”模块中的PSWF 脉冲，进行调制。其中第一路中“direct sine table”模块存储的是第一阶PSWF 脉冲，以此类推，调制的路数决定了一共选择脉冲的个数。各路信息调制到PSWF 脉冲上后，经过相加器得到合成的信号，从端口“out1”发出。图7 从上至下依次是第1路调制信号、第3 路调制信号、合成后信号的时域波形。图8 为合成信号的频谱图，主瓣从3 MHz 到3.003 MHz。

图6 调制模块

图7 第1 路、第3 路和合路的调制波形

图8 合成信号的频谱图

4)短波信道模块。模块结构如图9 所示。调制模块输出的信号，从端口“In1”进入信道模块。在信道模块中首先经过“Analytic Signal”模块，使其经过Hilbert 变换后，与原实信号合成复信号。然后将基于采样的格式转换为基于帧的格式，之后信号进入“Multipath Fading”模块和“AWGN”模块，这2 个模块构成了对短波信道特性的仿真。最后信号格式反变换为基于采样的格式，并取出其实部。图10 为经过信道后的时域波形图。

图9 短波信道模型

图10 经过信道后的时域波形

5)解调模块。模块结构如图11 所示。来自信道的信号通过端口“In1”进入到解调模块。通过“Buffer”将一个码元时间内的采样值一起输出，并且通过相乘器和存储在“direct sine table”模块中的PSWF 脉冲进行相关解调，得到各路数据，然后经过“Switch”模块将由1 和−1 组成的数据，对应为由1 和0 组成的数据。最后经端口“Out1”到“Out4”输出各路解调数据。

图11 解调模块

6)并串变换模块。模块结构如图12 所示。从解调模块输出的4 路信号分别由端口“In1”到“In4”输入，经过“Multiport Switch”模块，使并行的数据变为串行的数据流，由“Out1”输出。

图12 并串变换模块

4 仿真结果分析

假设短波信道的中心频率为3.001 5 MHz，信道带宽为3 kHz，码元持续时间为4 ms，时间带宽积为12π，采样频率为20 M，调制路数分别为6 路和12 路，传输路径为3 个，见表1，其中第1 径为主径。得到误码率和调制路数的关系如图13 所示，可以看出，不同的信噪比条件，6 路调制时的误码率要明显好于12 路调制时的误码率。这是因为调制路数增多时，PSWF 脉冲之间的正交性更易被破坏。短波信道的多径时延、多普勒频移、衰落以及噪声等因素对传输信号正交性的影响加剧。PSWF 脉冲之间的正交性变差，解调端正是利用PSWF 脉冲正交性进行相关解调，所以系统的可靠性出现下降。

表1 信道参数

图13 不同调制路数情况下误码率曲线

5 结论

利用Simulink 软件对基于PSWF 的非正弦短波通信原理样机实现之前的先验性仿真，较真实地反映了基于PSWF 的非正弦通信技术在短波频段内的特性。基于数据流的仿真，更加贴近原理样机的实现，预先反映出了样机实现中的问题。文中的重构方法可以完善地解决小相对带宽PSWF 脉冲的实现问题。为下步原理样机的实现提供了有力的支撑。

[1] 胡中豫. 现代短波通信[M]. 北京∶ 国防工业出版社, 2005∶1-7.

[2] 涂旭东. 宽带短波信道特性和建模研究[D]. 成都∶ 电子科技大学, 2004∶2-3.

[3] 舒根春. 基于椭圆球面波的非正弦通信研究[D]. 烟台∶ 海军航空工程学院, 2011∶1-3.

[4] 张传浩, 程健庆, 陈利风. 短波信道模型仿真实现及改进算法研究[J]. 指挥控制与仿真, 2009,31(6)∶76-78.

[5] 高珑. 短波宽带并行传输体制的研究[D]. 西安∶ 西安电子科技大学, 2009.

[6] 吴施其, 朱立东. 通信系统概论[M]. 北京∶ 清华大学出版社, 2005∶43-45.

[7] XIAO H, ROKHLIN V, YARVIN N. Prolate spheroidal wave functions, quadrature and interpolation[J]. Inverse Problems, 2001,17(4)∶805-838.

[8] REZA S DILMAGHANI, MOHAMMAD GHAVAMI, BEN ALLEN, et al. Novel UWB pulse shaping using prolate spheroidal wave functions[C]//14th IEEE International Symposium on Personal, Indoor & Mobile Radio Communication Proceedings. 2003∶602-606.

[9] KEDAR KHARE, NICHOLAS GEORGE. Sampling theory approach to prolate spheroidal wave functions[J]. Journal of Physics A∶ Mathematical and General, 2003(36)∶10011-10021.

[10] KEDAR KHARE. Bandpass sampling and bandpass analogues of prolate spheroidal functions[J]. Signal Processing, 2006(86)∶1550-1558.

[11] PARR B, CHO B, WALLACE K. A novel ultra- wideband pulse design algorithm[J]. IEEE Communica- tion Letters, 2003,7(5)∶219-221.

[12] 刘锡国, 王红星, 刘传辉, 等. 基于重构滤波的非正弦时域正交调制方法实现[J]. 吉林大学学报, 2012, 42(2)∶506-507.