数据链航迹与ESM间断航迹融合跟踪精度研究

王永安，李世忠，关成斌

（1．91880 部队，山东 胶州 266300；2．海军航空工程学院电子信息工程系，山东 烟台 264001）

近年来，机载传感器得到迅猛发展，所装备的传感器越来越多、越来越先进。如警戒雷达、红外传感器和电子支援措施(ESM)，特别是最新发展的空空、空地通信数据链和联合战术信息分配系统(JTIDS)等，已成为现代作战飞机了解态势环境的重要信息源。通过数据链装置横向进行机载多传感器的数据融合，实现对多个传感器探测信息的综合、分析和处理，达到资源共享，功能、性能相互弥补，得到目标状态、属性等战场态势信息，取得传统单平台单传感器无法完成的功能和效果[1]。同时大大减轻了简单增加传感器或提高传感器性能带来的种种矛盾，提高了对目标的探测概率，减小虚警率，受到了世界各国的广泛重视[2]。如美国的Link16、Link14、Link4A，以色列的ACR-740 等数据链实现了机载、陆基和舰载数据系统之间信息的交换[3-5]。通过ESM 系统与数据链系统的数据融合，可以提高对目标的探测和跟踪性能[2，6-7]。电子支援措施(ESM)在工作中能否获取关于目标的状态信息取决于对方辐射源的工作状态。因此，它获取的目标航迹信息往往是不连续的。数据链和ESM 数据融合是机载综合信息处理的一项重要内容，涉及多种因素，这些因素对数据链航迹和ESM 航迹融合精度影响如何是实际应用中面临的一个问题，本文研究了数据链航迹和ESM 间断航迹的融合流程和算法，并对影响数据链和ESM 融合精度的各种因素进行了仿真分析。

1 算法描述

1.1 数据链航迹+ESM 间断航迹融合流程

机载传感器通常使用数据链传送蓝机的航迹，且由于对方辐射源工作方式的限制，电子支援措施(ESM)得到的航迹往往是间断的，数据链航迹+ESM间断航迹融合算法流程如图1 所示，主要进行以下4 个步骤的处理。

图1 数据链航迹+ESM 间断航迹关联融合跟踪流程图

1)对ESM 点迹方位、俯仰上分别滤波，采用KF 滤波算法；

2)以ESM 航迹为基准进行时间对准，根据ESM航迹的时间情况，对数据链航迹进行外推或内插；

3)将数据链的目标航迹信息转换到红机NED坐标系；

4)利用ESM 方位、俯仰滤波后的航迹对数据链航迹进行状态更新得到融合航迹。

1.2 ESM 方位角、俯仰角滤波

对 ESM 测得的方位角、俯仰角分别采用Kalman 滤波器进行滤波，具体方法如下。

离散时间系统的动态方程可表示为

式中：F(k)为状态转移矩阵；X(k)为状态向量；G(k)为输入控制项矩阵；u(k)为已知输入或控制信号；V(k)是零均值、白色高斯过程噪声序列，其协方差为Q(k)；如果过程噪声V(k)用Γ(k)v(k)代替，则Q(k)变为Γ(k)qVT(k)，Γ(k)为过程噪声分布矩阵。

式中：kjδ为kronecker delta 函数，该性质说明不同时刻的过程噪声是相互独立的。

离散时间系统的量测方程为

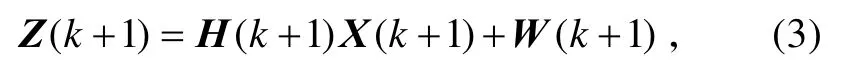
式中：H(k+1)为量测矩阵；W(k+1)为具有协方差R(k+1)的零均值、白色高斯量测噪声序列，

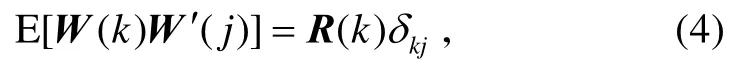
该性质说明不同时刻的量测噪声也是相互独立的。

式中，T为采样间隔。

初始协方差为

于是状态估计和滤波从k=2 时刻开始。

状态转移矩阵为

过程噪声分布阵为

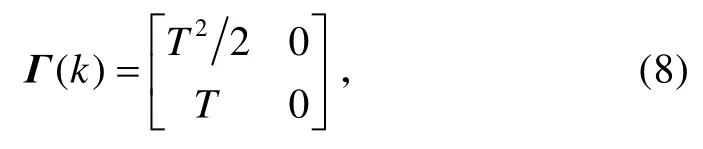
然后利用如下的Kalman滤波算法进行跟踪。

状态的一步预测为

协方差的一步预测为

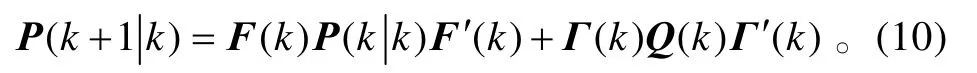
新息协方差为

增益为

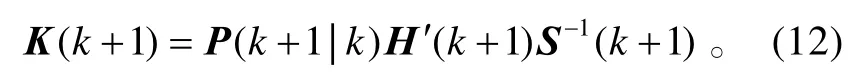
状态更新方程为

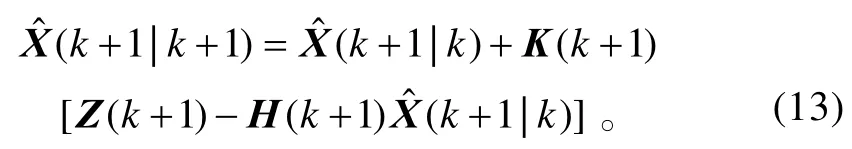
协方差更新方程为

1.3 内插、外推法时间配准算法

如果数据链航迹与ESM 航迹的数据率不一致，首先要进行时间对准；内插、外推时间配准方法认为时间对准就是在同一时间片内，对各传感器采集的目标观测数据进行内插外推，将高精度观测时间上的数据推算到低精度的观测时间点上，以达到2类传感器时间上的同步。在这里以ESM 航迹为基准，对数据链航迹使用内插、外推法进行时间对准。该方法的步骤如下：

1)选取时间片TM，时间片的划分随具体的运动目标而异，目标的状态可以分为静止、低速运动和高速运动，相应的进行融合的时间片就可以选取为小时、分钟和秒级；

2)将各传感器的观测数据按测量精度进行增量排序；

3)将高精度的观测数据向低精度的时间点内插、外推，以形成一系列等间隔的目标观测数据。同一时间片内的观测数据通常有多个，如图2 所示。

图2 内插、外推法时间配准算法示意图

由高精度的时间点a向低精度时间点b的归结算法如下：

式中，X分别为x、y、z三个方向的坐标。

而对于速度的外推，可假设在同一时间片内，目标作匀速直线运动，则由时间点t1外推至时间点t2速度不变，即vt1=vt2。

1.4 航迹融合算法

1)数据链直角坐标系下量测误差转换为极坐标系下角度量测误差。因为k时刻目标的数据链位置量测值(x(k)、y(k)、z(k))和方位、俯仰转换量测值(α(k)、γ(k))有如下的关系：

对式(16)分别对x、y、z上求偏导可得：

由式(18)可以求出数据链在方位和俯仰上的等效测量误差。

2)在时间对准以后，按照方差加权方法对同一采样时刻的αData(k)、αESM(k) 进行数据压缩，则在该时刻目标的方位角为[8]

同理可对俯仰角γData(k)、γESM(k) 进行压缩。

2 仿真结果分析

红方两架飞机编队飞行，红机上搭载雷达和ESM 两种传感器，友机给红机传来数据链航迹，蓝方两架飞机编队飞行。红机作为融合中心，在NED坐标系下处理数据，融合后输出结果。

仿真时间100 s，导航数据的数据率0.1 s；融合后输出数据的周期0.5 s；蓝机1 地理坐标初始位置纬度、经度、高度分别为[36.1, 120, 8 111.3]，初始速度X、Y、Z方向分别为[300, 300, 0]；蓝机2地理坐标初始位置纬度、经度、高度分别为[36.1, 119.4, 8 347.9]，初始速度X、Y、Z方向分别为[500, 500, 0]；蓝机1 与红机距离100 km，友机与红机距离30 km；红机地理坐标初始位置纬度、经度、高度分别为[36.1,x, 5901.5]，初始速度X、Y、Z方向分别为[300, 300, 0]；友机地理坐标初始位置纬度、经度、高度分别为[36.1,x, 9 499.9]，初始速度X、Y、Z方向分别为[300, 300, 0]；数据链测量周期T1D= s，数据链量测等间隔间断3 次，每次间断一个量测点； ESM 测量周期E0.1T=s，等间隔间断8 次，ESM关机时间占总工作时间的20%；Monte Carlo 仿真100 次。

2.1 传感器误差对跟踪精度的影响分析

设数据链X、Y、Z方向上均方根误差相同σX=σY=σZ，且其均方根误差记为σXYZ；ESM 方位角、俯仰角测量精度相同，且其均方根误差记为σAP，目标与红方飞机均匀加速直线飞行，分3 种情况进行仿真，见表1，数据链精度、ESM 精度依次下降。仿真结果如图3~8 所示。

表1 仿真场景

图3 场景1 距离精度比较

图4 场景1 位置精度比较

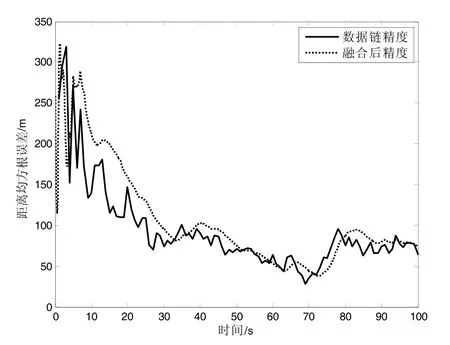
图5 场景2 距离精度比较

图6 场景2 位置精度比较

图7 场景3 距离精度比较

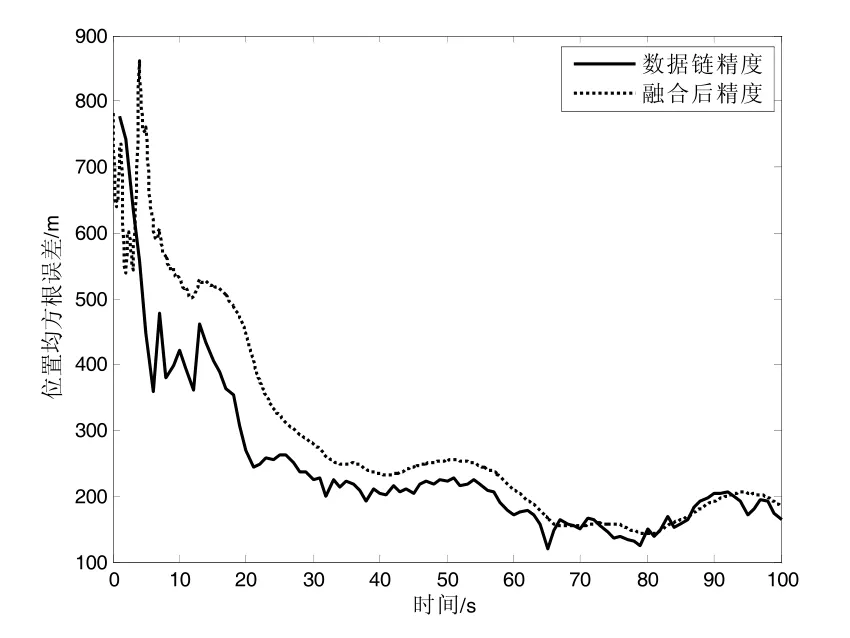
图8 场景3 位置精度比较

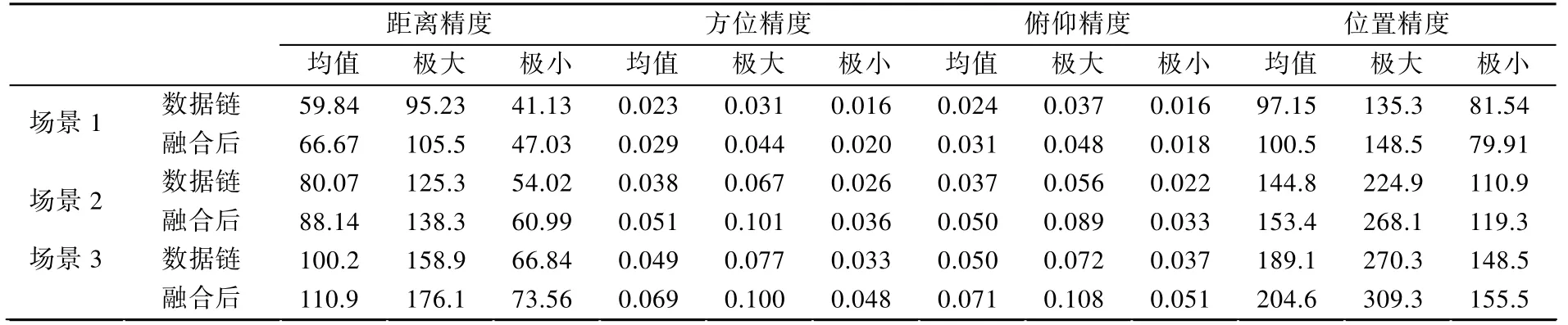
表2 各场景下滤波平稳后，数据链精度与融合后精度比较

1)从图3、5、7 和表2 中场景1、2、3 的精度对比可以看出：数据链精度分别是200、300、400时，融合前后的距离精度均值分别是(59.84，66.67)、(80.07，88.14)、(100.2，110.9)，数据链航迹和融合后航迹的精度与随着数据链误差的增大而下降。

2)从图4、6、8 和表2 中场景1、2、3 的精度对比看出：数据链精度分别是200、300、400 时，融合前后的位置精度均值分别是(97.15，100.5)、(144.8，153.4)、(189.1，204.6)，数据链航迹和融合后航迹的精度与随着数据链误差的增大而下降。

在仿真中发现：场景1、2、3 中ESM 的测角精度都低于数据链转换后的测角精度，融合后的位置精度差于数据链的位置精度。

2.2 传感器数据率对跟踪精度的影响分析

设在整个跟踪过程中，数据链X、Y、Z方向上均方根误差σX=σY=σZ=400 m；ESM 方位角、俯仰角均方根误差为σA=σP=0.3°。分以下4 种情况进行分析，见表3，仿真结果如图9~16 所示。

表3 各场景下数据链测量周期和ESM 测量周期

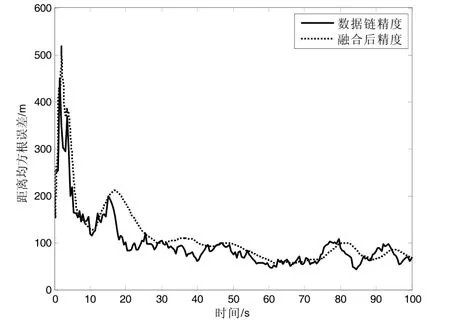
图9 场景1 距离精度比较

图10 场景1 位置精度比较

图11 场景2 距离精度比较

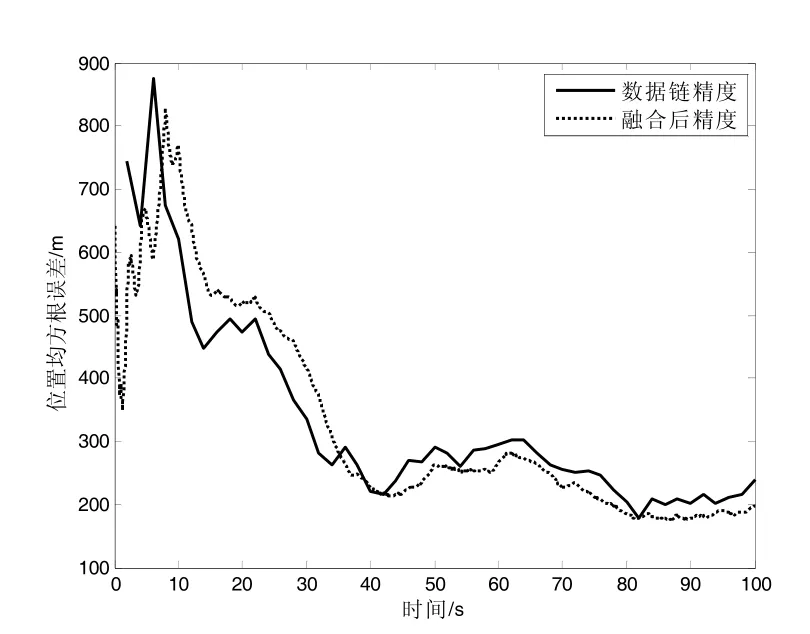
图12 场景2 位置精度比较

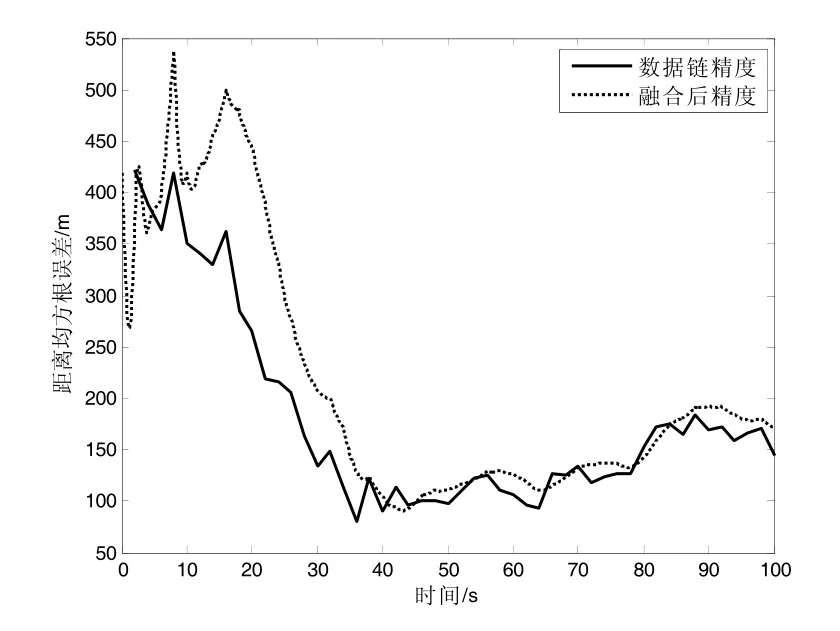
图13 场景3 距离精度比较

图14 场景3 位置精度比较

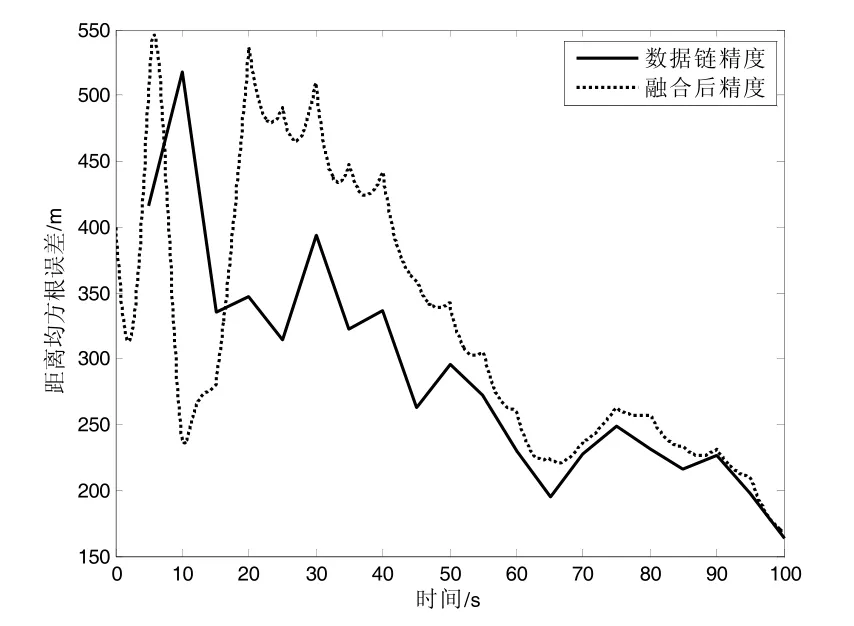
图15 场景4 距离精度比较

图16 场景4 位置精度比较

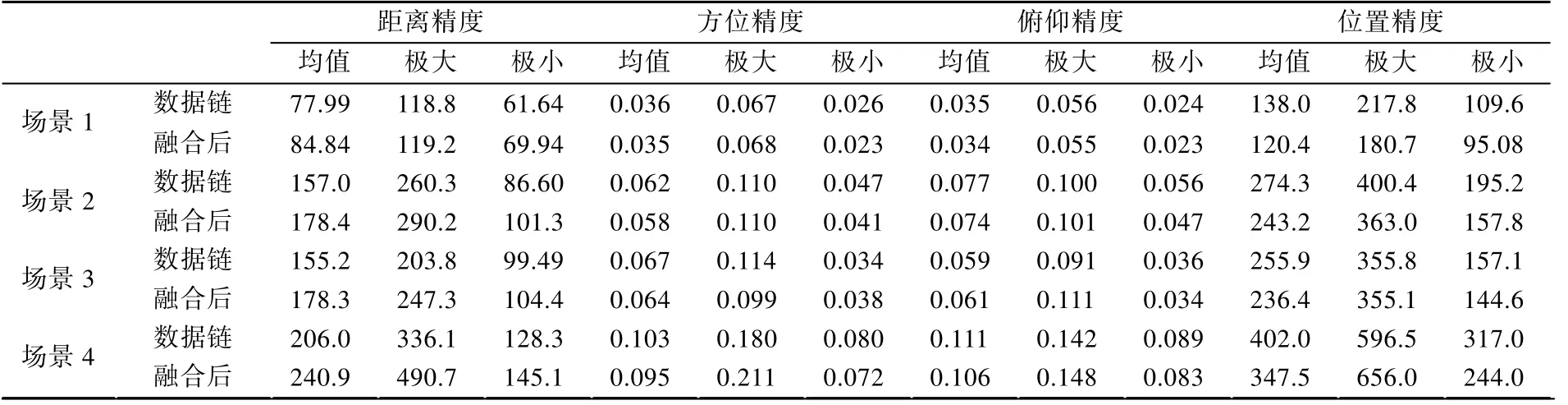
表4 各场景下滤波平稳后，数据链精度与融合后精度比较

1)从图9、10(TD=0.5)、图13、14(TD=1)与图15、16(TD=5)和表2 中场景1、3、4 的各种精度数据可知，数据链的数据率从0.5 s 下降到1 s 再到5 s一个数据时，其跟踪精度明显下降，融合后的精度在测距精度上从84.84 m 下降到178.4 m 再到240.9 m，位置精度从120.4 m 下降到236.4 m 再到347.5 m。

2)从图13(TE=0.05)、15(TE=0.1)和表4 中场景2、3 的位置精度数据可知，当数据链的数据率不变时，提高ESM 的数据率对跟踪精度的影响并不明显。这说明融合后的精度主要由数据链的数据率决定，与ESM 的数据率关系不大。

2.3 平台运动特性对跟踪精度的影响分析

数据链X、Y、Z方向上σX=σY=σZ=0.3km，测量周期TD= 1s；ESM 方位角、俯仰角均方根误差为σA=σP=0.3°，ESM 测量周期TE=0.1s。除说明，以下仿真均按此条件给出。分4 种情况进行分析，见表5，仿真结果如图17~24 所示。

表5 各场景下的平台运动方式

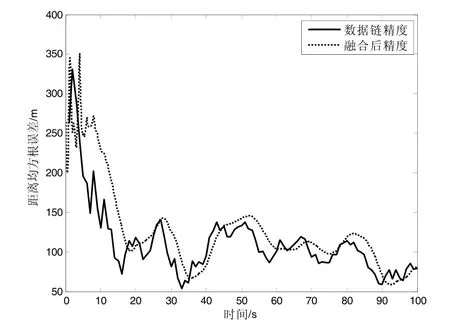
图17 场景1 距离精度比较

图18 场景1 位置精度比较

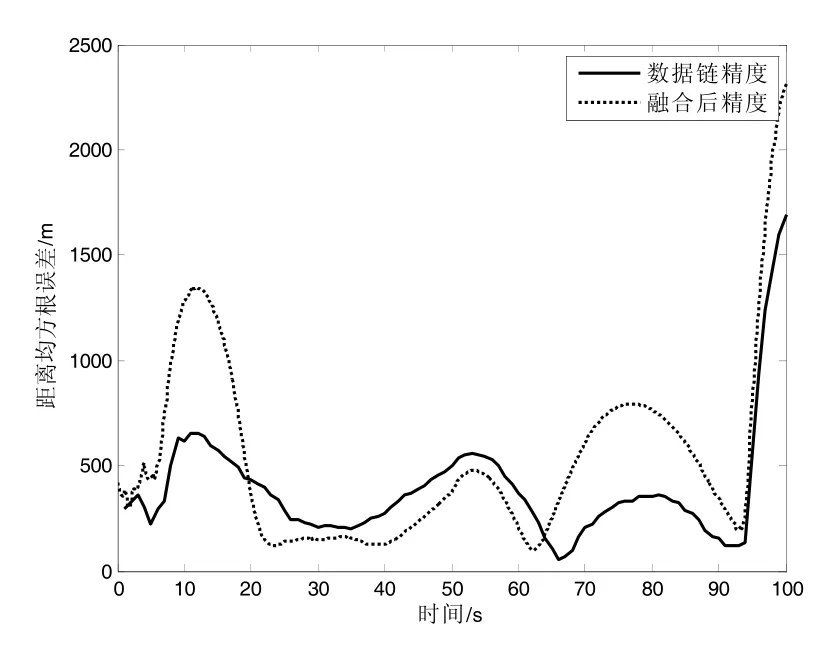
图19 场景2 距离精度比较

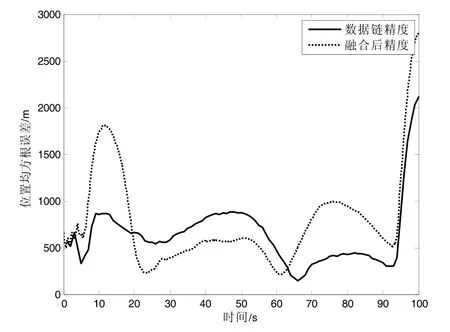
图20 场景2 位置精度比较

图21 场景3 距离精度比较

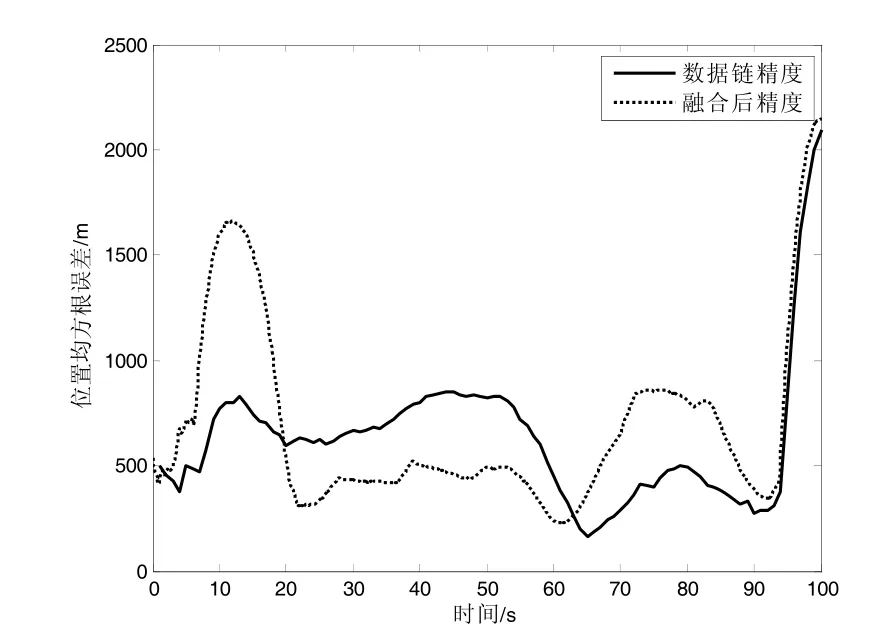
图22 场景3 位置精度比较

图23 场景4 距离精度比较

表6 各场景下滤波平稳后，数据链精度与融合后精度比较

由仿真结果可得如下结论：

1)比较图18、20、22、24 和表6 中场景1、2、3、4 可知，蓝机和红机在相同方向上同时做匀加速直线运动或者之字形运动(场景1、4)，相对的加速度为0 时，融合后的位置精度均值分别是139.1 m和139.6 m，跟踪精度较高；蓝机做匀加速直线运动而红机做之字形运动或者蓝机做之字形运动而红机做匀加速直线运动(场景2、3)，存在相对的加速度时，融合后的位置精度均值分别是880.8 m 和882.4 m，跟踪精度较差。

2)比较图20、24 和表6 中场景2、4 可知，当蓝机做之字形运动时，红机以匀加速直线和之字形跟踪位置精度均值分别是880.8 m 和139.6 m，红机以之字形跟踪可以提高融合精度。

3)比较图18、22 和表6 中场景1、3 可知，当蓝机匀加速直线运动时，红机以匀加速直线和之字形跟踪位置精度均值分别是139.1 m 和882.4 m，红机以之字形运动方式跟踪，存在相对的加速度，对提高融合精度没有帮助。

3 结论

本文针对数据链航迹和间断ESM 航迹关联融合的情况，通过仿真研究了不同精度、不同数据率和不同平台运动特性对融合精度的影响，研究表明，ESM 的测角精度通常低于数据链转换后的测角精度，融合后的位置精度也通常低于数据链的位置精度，当数据链的数据率不变时提高ESM 的数据率对跟踪精度的影响并不明显。这些结论对实际的机载数据融合处理具有一定的参考和借鉴价值。

[1] 李勇, 王德功, 常硕. 基于多传感器数据融合的飞机目标自动敌我识别方法[J]. 四川兵工学报, 2012,33 (1):33-35.

[2] 黄鹤. 机载多传感器数据融合的数据链应用技术[J]. 电讯技术, 2004,(4):103-106.

[3] TRANI P, ANTOINE P. MPM for radar data link and ECM systems[C]. Kitakyushu: IEEE, IVEC, 2007:403- 404.

[4] SCHMITT M. Coordinating the global information grid initiative with the NG9-1-1 initiative[C]. Bangkok. Thailand: IEEE, ICMIT, 2008:415-420.

[5] 陈颖, 成晓岚. 数据链在外军装备中的应用及关键技术[J]. 航空电子技术, 2004,35(4):43-48.

[6] RONG LANG, WANG WEICHANG, LOGAN M, et al. Multiplatform multisensor fusion with adaptive-rate data communication[J]. IEEE Trans. on AES, 1997,33 (1):274-281.

[7] GONZALES D, HOLLYWOOD J, KINGSTON G. Network-centric operations case study: air-to-air combat with and without link 16[R]. Santa Monica, CA, USA: RAND National Defense Res. Insti. Santa Monica, 2005.

[8] 何友, 王国宏, 等. 多传感器信息融合及应用[M]. 2版. 北京: 电子工业出版社, 2007:212-233.