弹性支撑及连接边界的多跨曲梁面内自由振动分析
周海军,李玩幽,吕秉琳,李文龙
(1.哈尔滨工程大学动力与能源工程学院,黑龙江哈尔滨150001;2.韦恩州立大学机械工程学院,底特律48202)
曲梁结构以其结构简单、强度高等特点在现代土木、航天、船舶、汽车等领域得到越来越多的应用,在其多样的结构振动中尤其又以面内振动引起了众多国内外学者的关注.孙建鹏等[1]采用传递矩阵法求解了单跨曲线箱型截面梁的固有特性.袁驷等[2]对平面变截面曲梁面内自由振动的自适应有限元法进行了求解分析.武兰河等[3]通过微分容积法将曲梁自由振动的控制微分方程和边界方程离散成为一组齐次线性方程组的典型特征值问题,求解得到曲梁自由振动特性.Chidamparam[4]等采用迦辽金法对弓形结构的面内振动进行了研究.众多学者采用有限元法对各种结构的曲梁进行了研究[5-7].Kang等[8]采用波传播方法对面内曲梁系统的自由振动进行了研究.李天匀等[9]、单德山等[10]在振动特性的基础上进一步研究了曲梁结构的功率流及曲梁结构梁桥的车桥耦合振动.
李文龙[11]提出了一种改进傅里叶级数方法分析任意支撑边界的直梁振动特性,并将其引入多跨直梁及任意边界板结构分析[12-14].
本文基于李提出的方法,对多跨曲梁面内自由振动特性进行求解分析.将曲梁面内径向和切向位移函数表示成傅里叶级数加上一个辅助多项式函数的形式.采用瑞利-里茨方法求解基于能量原理的哈密顿方程,得到关于未知位移幅值系数的标准特征值问题.将支撑及连接边界定义为各个方向的弹性刚度,可以通过设定数值大小简单地实现对各种传统边界的模拟,同时可以研究在弹性支撑与连接下的固有特性.
1 多跨曲梁理论
如图1所示的多跨曲梁结构,其支撑及连接都由弹性刚度提供.ki,w0和 ki,w1,Ki,w1和 Ki,w0,ki,μ0和ki,u1分别为第i段曲梁在左右两端的径向,扭转,切向支撑刚度分别为第i和i+1段曲梁之间3个方向的连接刚度.
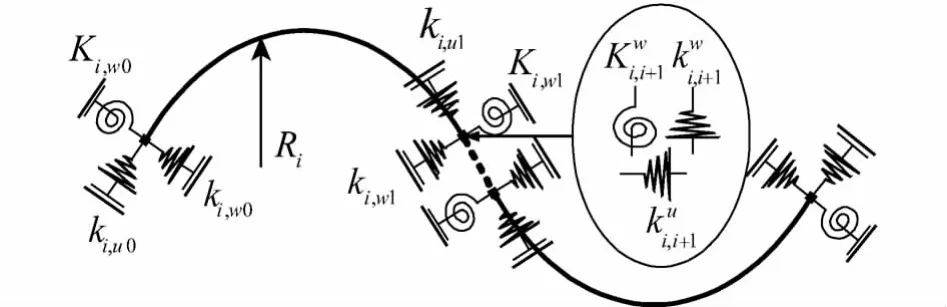
图1 多跨曲梁模型Fig.1 Model of multi-curved beams
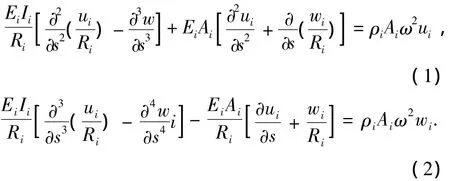
其面内振动控制微分方程为
式中:ui、wi、Ei、Ii、Ri、ρi和Ai分别为切向位移、径向位移、杨氏模量、惯量、半径、密度和截面积,s为曲线坐标,ω为圆频率.
其应变εi,转角φi,曲率变化χi可以表示为
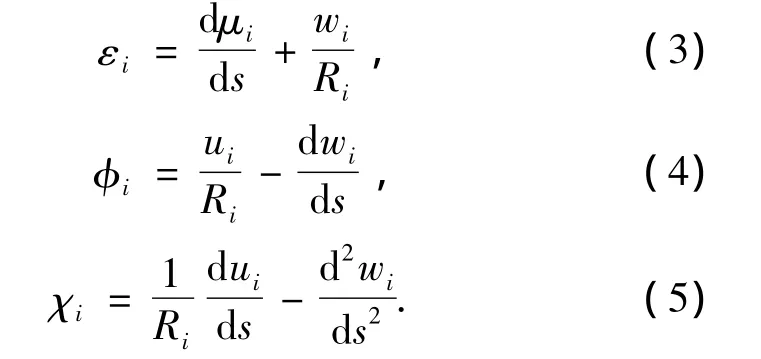
将切向和径向位移写成如下形式:
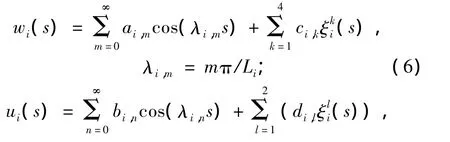

其中,
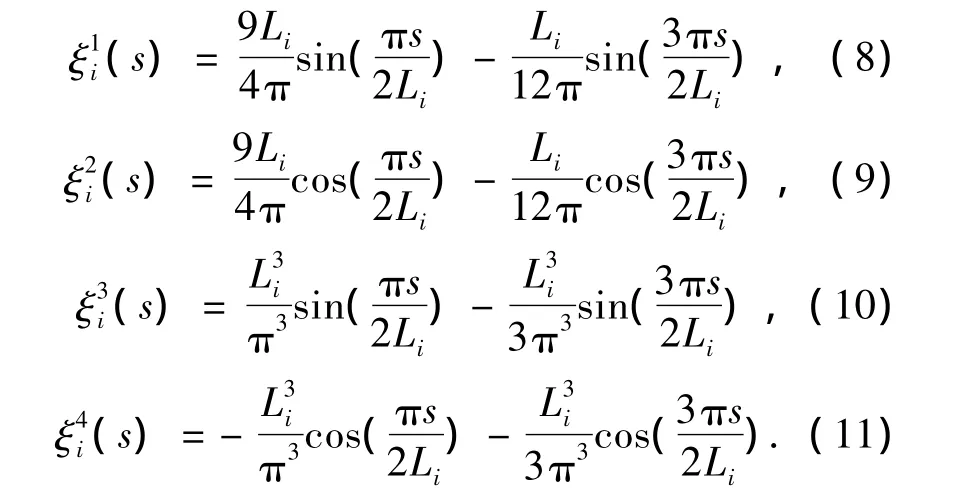
基于能量原理的哈密顿方程表示为
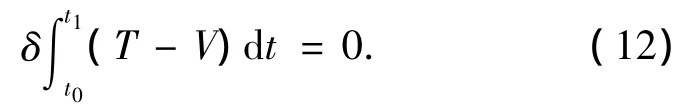
其中将总的势能V定义为
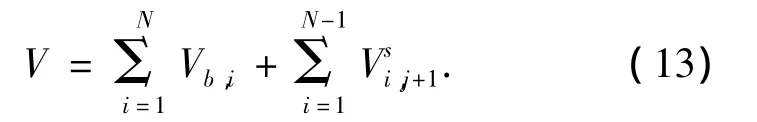
式中:N表示曲梁跨数.
将总的动能表示为
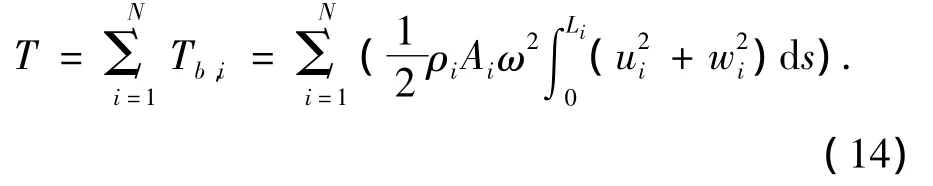
在式(13)中Vb,i表示曲梁i的势能:
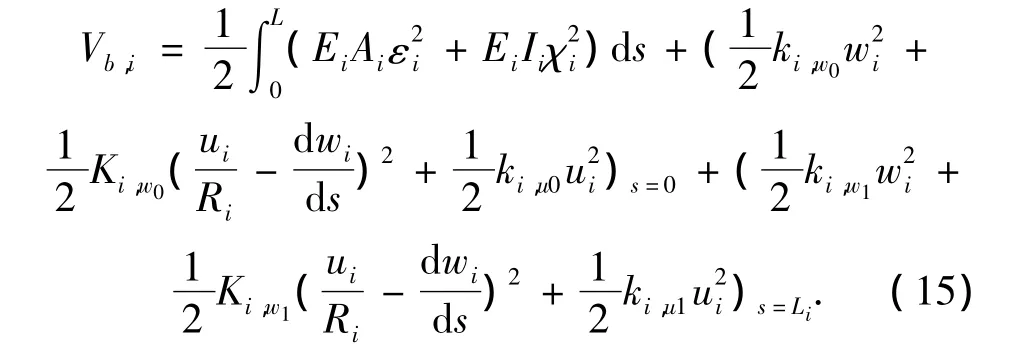
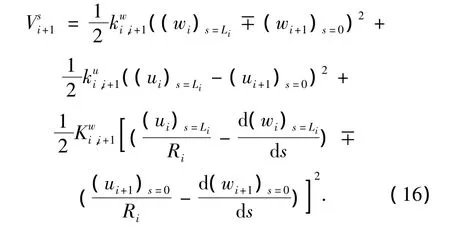
式中:右边第1、3项括号内为负号时表示曲梁i和i+1有相同的曲率法线方向时的表达式;而正号为相反时的表达式.
根据瑞利-里茨方法求解,先将位移表达式(6)、(7)代入式(13)、(14),之后对每个未知幅值系数求导并令其等于0.例如,当有相同曲率时对未知系数ai,m'求导得到的方程为
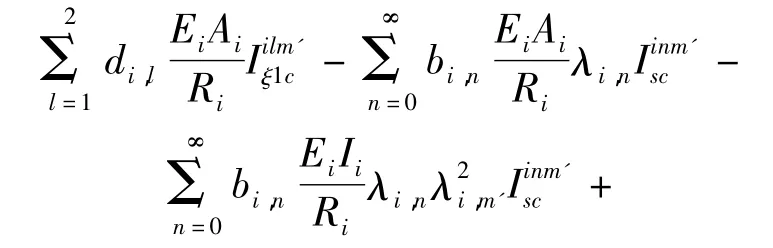
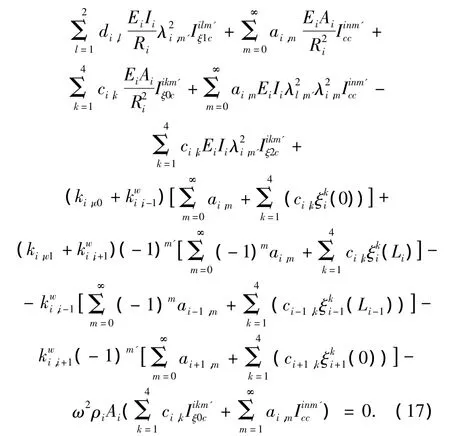
其中:
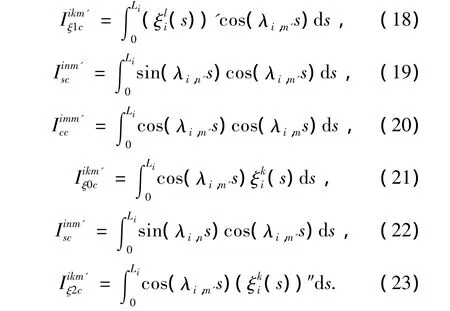
其他未知系数的求导表达式不再一一给出.
将式(6)、(7)中的傅里叶级数展开截断到m= M和n=N之后,将求导得到的方程整理成矩阵表达形式:
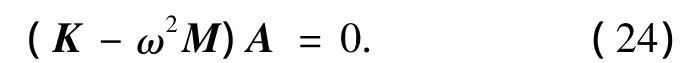
2 单跨及双跨曲梁结果分析
首先考虑一个在不同传统边界,即在固支,简支及自由边界条件下单跨曲梁的振动特性,其参数为: E=2.1×1011Pa,I=7.854 0×10-9m4,R=1 m,ρ=7 800 kg·m-3,A=3.141 59×10-4m2,以及L =1.047 2 m(即一个半径为1 m,跨度为60°的曲梁长度).文中傅里叶级数展开到M=N=20.将弹簧刚度系数设置为0或一个无穷大数可以模拟自由或固支边界,本文数值取k=1×1012N·m-1.表1~3列出了其前10阶固有频率与在有限元软件ANSYS中仿真结果的对比.有限元模型中曲梁划分成30个单元.
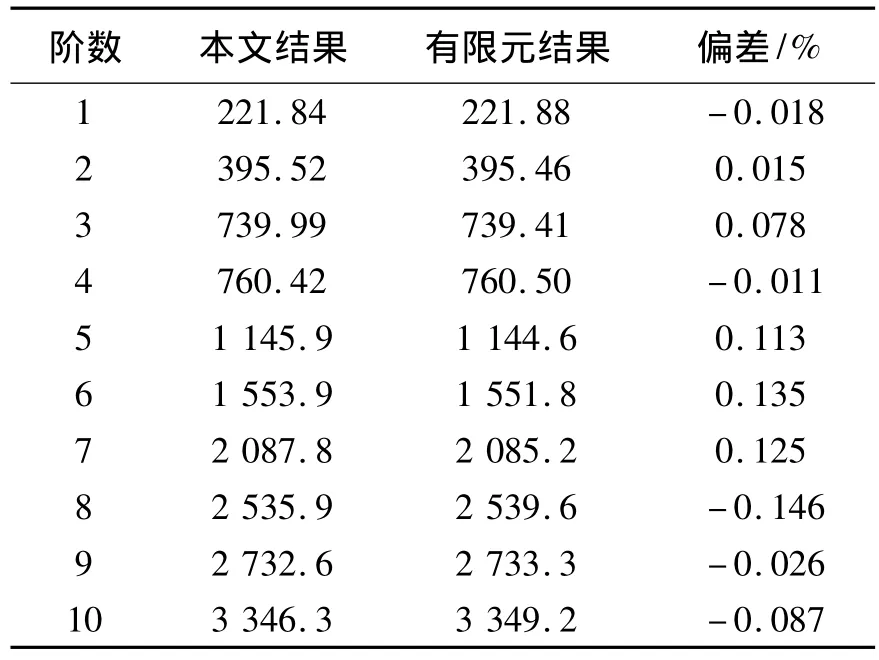
表1 单跨曲梁固支边界结果对比Table 1 The comparing results of a single-span curved beam with C-C boundary conditions
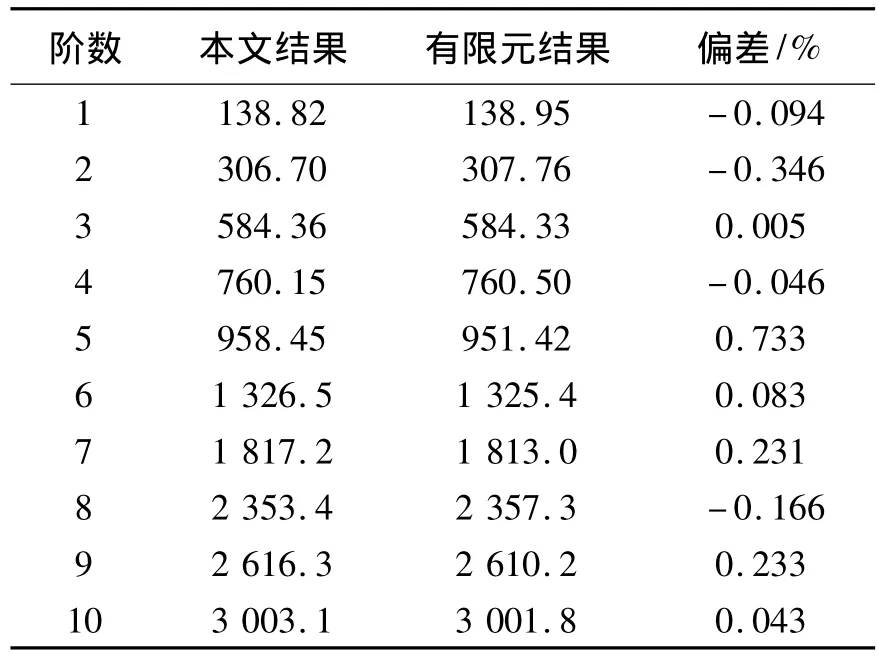
表2 单跨曲梁简支边界结果对比Table 2 The comparing results of a single-span curved beam with S-S boundary conditions
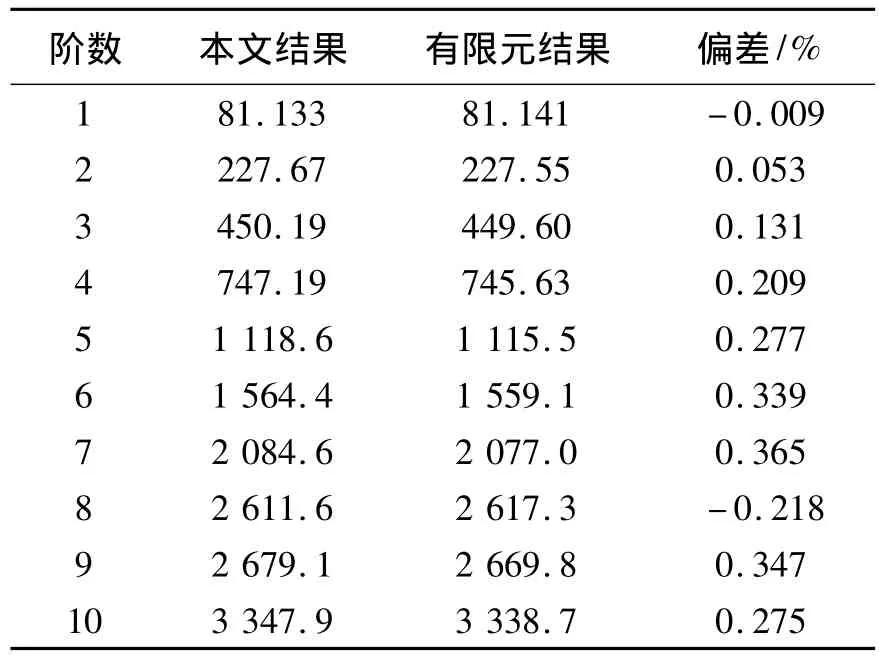
表3 单跨曲梁自由边界结果对比Table 3 The comparing results of a single-span curved beam with F-F boundary conditions
图2为固支边界前四阶振型与ANSYS所得振型的对比.将其振型分解到整体坐标x,y方向,归一化到1之后进行对比.由固有频率和振型的对比可以看出本文方法是正确的.
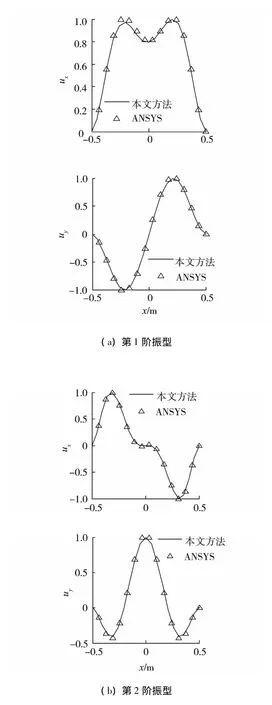
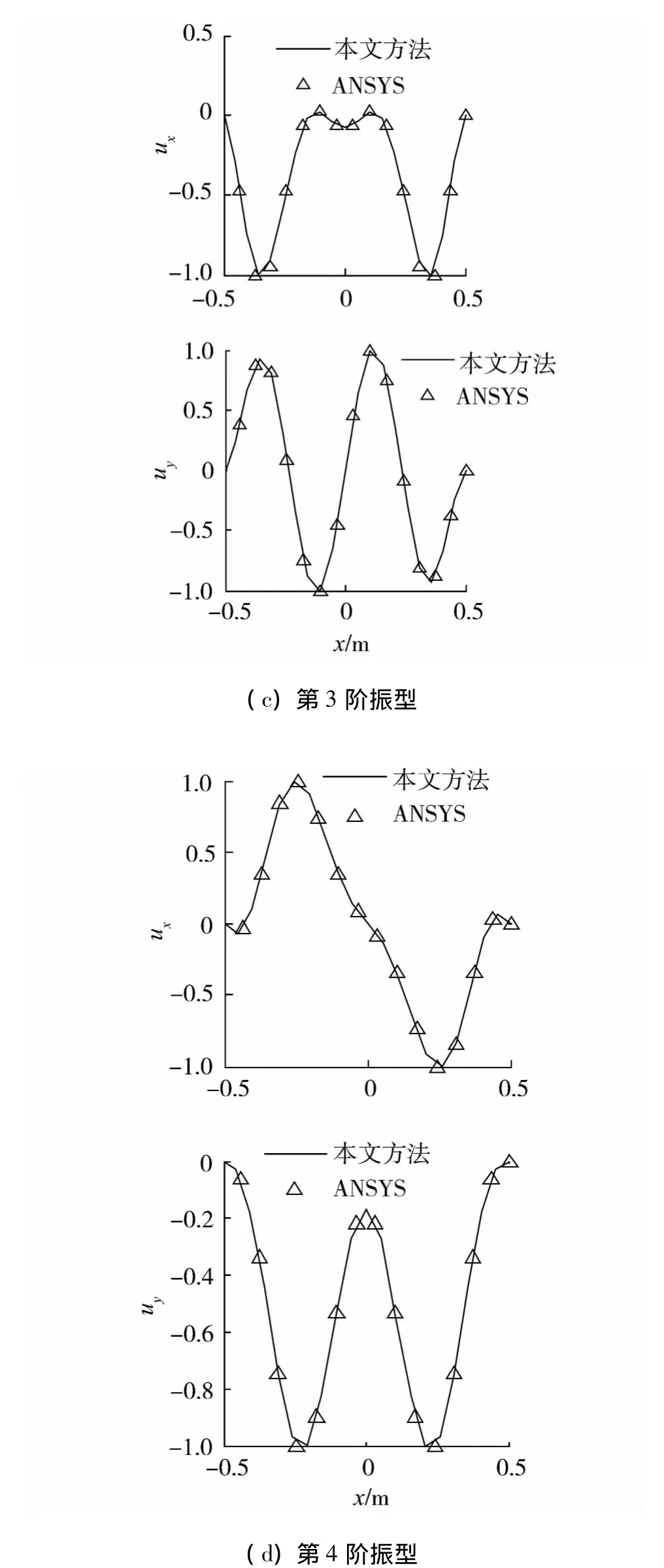
图2 前四阶振型与有限元的对比Fig.2 The first four mode shapes compared with FEA results
选取一个L=1.570 8 m(即一个半径为1 m,跨度为90°的曲梁长度),其他参数同上一个算例,将径向和切向支撑刚度设定为k=5×105N·m-1,扭转支撑刚度设定为k=0 N·m-1以模拟弹性支撑边界.其前10阶固有频率与在有限元软件ANSYS中仿真结果的对比见表4,可见弹性边界结果也是正确的.
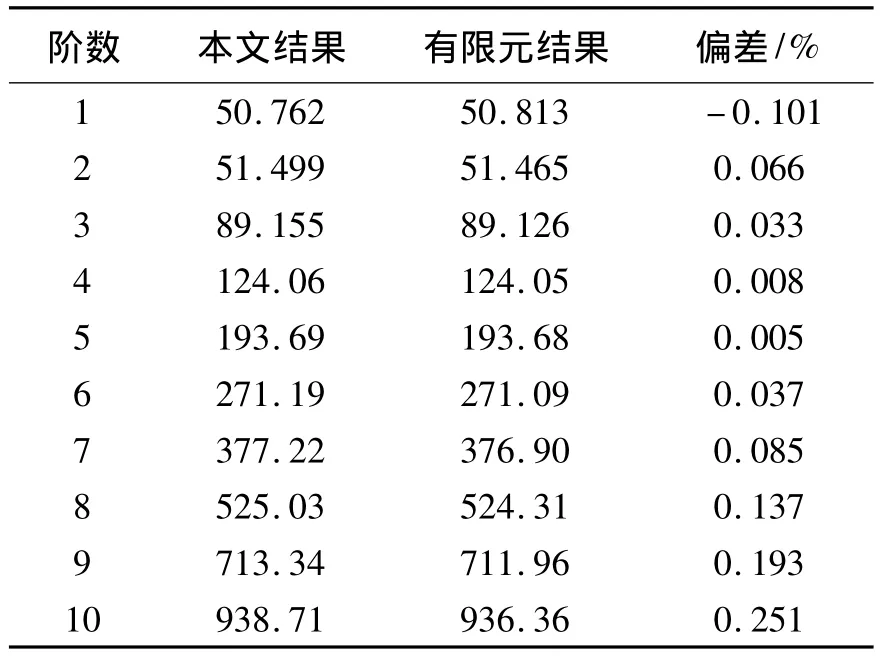
表4 单跨曲梁弹性边界结果对比Table 4 The comparing results of a single-span curved beam with elastic boundary conditions
为了验证本文在多跨曲梁处理的正确性,选择了一个两跨曲梁模型,每跨曲梁的参数都与第1个算例相同,两跨曲梁拥有相反的曲率方向.两端边界取为固支边界,连接刚度也取为刚性,其刚度参数设置具体为:k1,w0=K1,w0=k1,u0=1×1012N·m-1,k2,w1=K2,w1=k2,u1=1×1012N·m-1,k1,w1=K1,w1=k1,u1=0 N·m-1,k2,w0=K2,w0=k2,u0=0 N·m-1以及.表5列出了其前10阶固有频率与有限元软件ANSYS中仿真结果的对比.
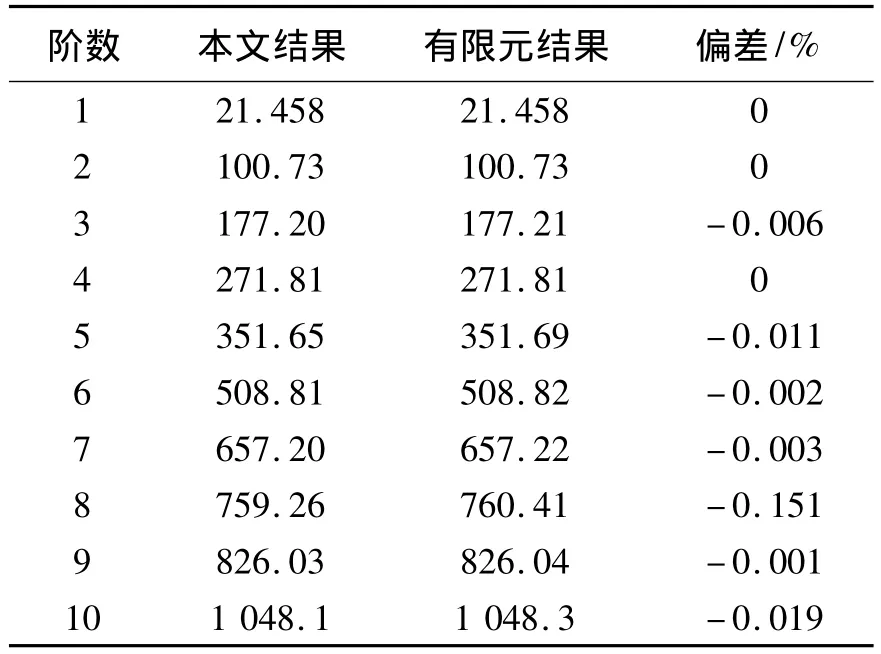
表5 双跨曲梁固支边界结果对比Table 5 The comparing results of a two-span curved beams with C-C boundary conditions
图3列出了前四阶振型.图3(a)中为第1和第3阶振型,为对称振型;图3(b)中为第2和第4阶振型,为反对称振型.可以看出在多跨曲梁的处理上也是正确的.
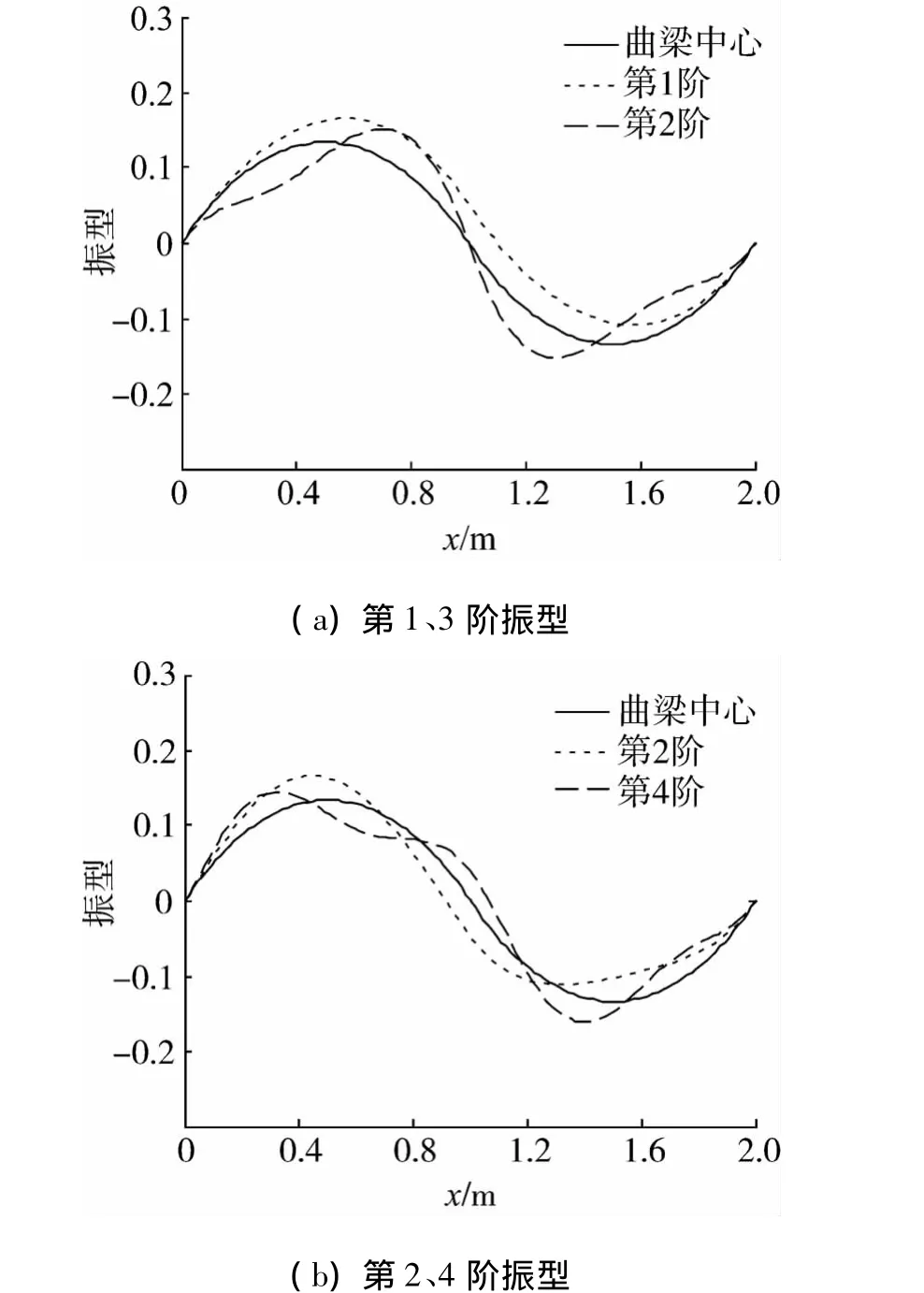
图3 前四阶振型Fig.3 The first four mode shapes
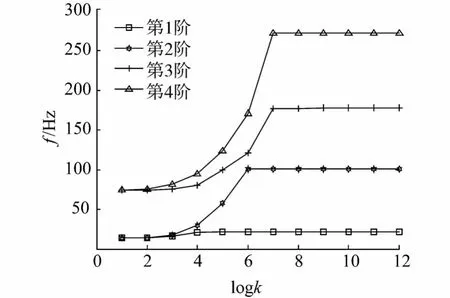
图4 两跨曲梁中间连接刚度对其前4阶频率的影响Fig.4 The effect of connecting stiffnesses between twospan curved beams on the first four frequencies
3 结论
本文采用一种改进的傅里叶级数方法,对多跨曲梁面内自由振动特性进行求解分析.采用瑞利-里茨方法求解基于能量原理的哈密顿方程,得到关于未知位移幅值系数的标准特征值问题.将支撑及连接边界定义为各个方向的弹性刚度,可以通过设定数值大小简单地实现对各种传统边界的模拟,同时改变连接弹簧势能中的正负号可以模拟具有相同或相反曲率法线方向的多跨曲梁.求解了单跨固支、简支、自由边界及弹性支撑边界模型结果及两跨固支、相反曲率法线方向模型的结果,通过与有限元软件ANSYS模型所得结果的对比验证了方法的正确性.并分析了两跨固支曲梁中间连接刚度对固有频率的影响,中间连接刚度的降低首先影响到高阶频率,并且都在某个刚度区域发生频率的突然变化.
[1]孙建鹏,李青宁.基于传递矩阵法曲线桥的振动特性分析[J].西安建筑科技大学学报:自然科学版,2009,41 (4):518-523.
SUN Jianpeng,LI Qingning.The vibration characteristic analysis of curved bridge based on transfer matrix method[J].Journal Xi'an University of Architecture&Technology:Natural Science Edition,2009,41(4):518-523.
[2]袁驷,叶康生,王珂.平面曲梁面内自由振动分析的自适应有限元法[J].工程力学,2009,26(增刊):126-132.
YUAN Si,YE Kangsheng,WANG Ke.A self-adaptive FEM for free vibration analysis of planar curved beams with variable cross-sections[J].Engineering Mechanics,2009,26(Suppl.):126-132.
[3]武兰河,刘淑红,周敏娟.圆弧曲梁面内自由振动的微分容积解法[J].振动与冲击,2004,3(1):117-122.
WU Lanhe,LIU Shuhong,ZHOU Minjuan.Differential cubature method for in-plane vibration analysis of shear deformable curved beams[J].Journal of Vibration and Shock,2004,3(1):117-122.
[4]CHIDAMPARAM P,LEISSA A W.Influence of centerline extensibility on the in-plane free vibrations of loaded circular arches[J].Journal of Sound and Vibration,1995,183: 779-795.
[5]YANG S Y,SIN H C.Curvature-based beam elements for the analysis of Timoshenko and shear-deformable curved beams[J].Journal of Sound and Vibration,1995,187: 569-584.
[6]RAVEENDRANATH P,SINGH G,PRADHAN B.Free vibration of arches using a curved beam element based on a coupled polynomial displacement field[J].Computers and Structures,2000,78:583-590.
[7]YANG F,SEDAGHATI R,ESMAILZADEH E.Free inplane vibration of general curved beams using finite element method[J].Journal of Sound and Vibration,2008,318: 850-867.
[8]KANG B,RIEDEL C H,TAN C A.Free vibration analysis of planar curved beams by wave propagation[J].Journal of Sound and Vibration,2003,260:19-44.
[9]李天匀,张小铭.周期简支曲梁的振动波和功率流[J].华中理工大学学报,1995,23(9):112-115.
LI Tianun,ZHANG Xiaoming.The vibration wave and power flow in a periodical simply supported curved beam[J].Journal of Huazhong University of Science&Technology,1995,23(9):112-115.
[10]单德山,李乔.铁路曲线连续梁车桥耦合振动研究[J].振动与冲击,2005,24(4):62-67.
SHAN Deshan,LI Qiao.Vibration analysis of railway continuous curved-girder bridge coupled with vehicles[J].Journal of Vibration and Shock,2005,24(4):62-67.
[11]LI W L.Free vibration of beams with general boundary conditions[J].Journal of Sound and Vibration,2000,237:709-725.
[12]DU J T,LI W L,JIN G Y,et al.An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges[J].Journal of Sound and Vibration,2007,306:908-927.
[13]XU Hongan,LI W L.Vibrations of multi-span bridges under a moving load:effect of the coupling conditions between spans[J].Journal of Sound and Vibration,2008,312:736-753.
[14]ZHANG X,LI W L.Vibrations of rectangular plates with arbitrary non-uniform elastic edge restraints[J].Journal of Sound and Vibration,2009,326:221-234.

