竞争型径向基过程神经网络时序分类器

葛利，印桂生

(1.哈尔滨工程大学计算机科学与技术学院，黑龙江 哈尔滨150001;2.哈尔滨商业大学 计算机与信息工程学院，黑龙江哈尔滨150028)

基于过程神经网络的广泛应用背景及径向基函数神经网络在各领域的成功应用，文献［1］提出了径向基过程神经元网络的概念和模型，该模型在保留径向基函数神经网络优势的基础上，引入了过程神经元的概念，因此具有二者的优势.时序问题在客观实际中普遍存在，许多分类问题具有时序背景，即这些系统的输入是依赖于时间变化的函数，其归属类别的确定既依赖于输入函数的空间聚合，又与时间累积效应密切相关.依据以上背景，本文在径向基过程神经元网络的基础上，提出了一种竞争型径向基过程神经网络时序分类器，将时间累积效应充分考虑到时序分类器设计中，给出了竞争过程神经元单元的定义，网络拓扑结构和学习算法.

1 竞争型径向基过程神经网络模型

1.1 竞争过程神经元单元

竞争过程神经元单元结构如图1所示，由聚合运算、模式匹配、激励运算和竞争4部分组成.图1中，X(t)=［X1(t)X2(t) … Xn(t)］T为竞争过程神经元单元在某一时间延迟区间［0，T］上的输入函数，∫为聚合算子，K(·)为竞争过程神经元单元核函数，φ为竞争算子，其输入为所有径向基过程神经元的输出，其输出依据式(1)原则［2］，即当神经元被激活时，只有一个竞争神经元有较大输出，而其他神经元都被抑制.最大输入对应的神经元输出为1，其它所有神经元的输出均为0.

图1 竞争过程神经元单元图Fig.1 Competition process neuron unit

竞争过程神经元单元的输入、输出关系如下:

式中:y代表竞争过程神经元单元的输出，Oj为过程神经元j的输出:

式中:‖·‖为某一范数，Xj(t)为径向基过程神经元j的核中心函数［1］.

1.2 竞争型径向基过程神经网络模型

竞争型径向基过程神经网络为一种4层前向结构，输入层有n个节点，第2层为径向基过程神经元隐层，单元的变换函数是径向基核函数，第3层为竞争层，由第2、3层组成复合径向基过程神经元隐层，各层节点数均为m个，第4层为输出层，节点个数为k个，对应不同分类类别.网络拓扑结构如图2所示.

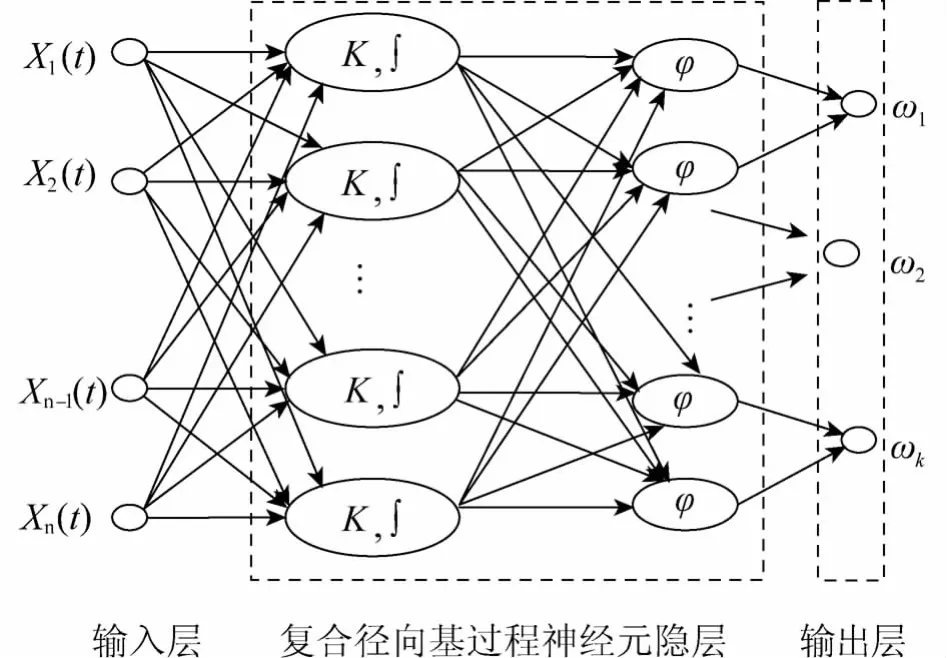
图2 竞争型径向基过程神经网络拓扑结构Fig.2 Competitive radial basis process neural network topology structure

其中，X(t)=［X1(t)X2(t)…Xn(t)］T为网络的输入，由复合径向基神经元隐层完成对时变输入时空特征的抽取和分类功能为所识别问题的m个标准模式函数，取Xj(t)为径向基过程神经元j的核中心函数［1］.竞争型径向基过程神经网络中，竞争过程神经元单元通过测量输入时变向量X(t)到所代表聚类区域的距离来决定时变向量X(t)属于哪个子类聚类.输出层的神经元标记代表模式样本的类别，其值由竞争过程神经元单元计算获得，无须计算所有竞争过程神经元单元输出的线性连接权值.

2 竞争型径向基过程神经网络的学习算法

竞争型径向基过程神经网络中需要优化的网络参数有:核函数个数、中心及宽度.给定一个训练样本集K={(Xm，n(t)，ωm)，1≤m≤k，1≤n≤numberm}，Xm，n(t)表示属于第m类的第n个时变样本输入，numberm表示第m类的样本个数，ωm为对应输出类别标记.

训练样本Xm，n(t)在同类样本中的密度估计函数的定义为

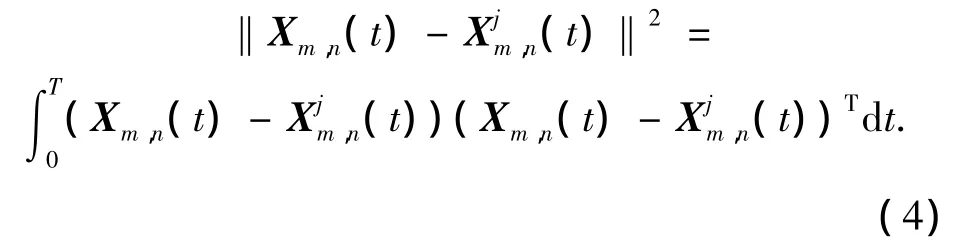
式中:rm，n表示样本Xm，n(t)与异类样本的最小距离.若一个训练样本周围有较多相同类别的样本点，则具有较大的密度值.

竞争型径向基过程神经网络时序分类器的训练算法如下:

1)首先将竞争型径向基过程神经网络输入时变函数和核中心函数展开为C［0，T］上的同一组标准正交基的展开式，依据数学分析理论及正交基性质，有式(5)成立［1］:

式中:L为在满足逼近精度的前提下，X(t)各分量标准正交基展开项数的最大值，n为X(t)的分量个数(即输入层节点个数)，ail、分别为X(t)和Xj(t)标准正交基展开项系数.

2)初始化所有训练样本标记设置为0，表示该训练样本没有被任何子类聚类包含，计算所有训练样本的密度.

3)对于每类样本，在未被包含的样本中选择具有最大密度值的样本作为聚类中心μi(t).计算中心到异类样本的最小距离，将其作为聚类半径ri.为每个聚类设置参数αi(0＜αi＜1)，用于调整每个聚类的大小.

4)依据式(5)计算每个样本到聚类中心的距离，依据式(6)标记样本

即样本到该中心的距离小于αi×ri，则将该样本输出值置为对应类别输出值，并标记为已被包含的样本.

5)重复4)，直到所有样本均被包含为止.

参数αi(0＜αi＜1)用来调整相邻2个子类聚类的重叠区域.所有聚类样本采用统一聚类参数显然不符合实际情况，因此针对各聚类样本训练的实际情况，根据样本到各聚类中心距离，动态调整各聚类的大小，最终得到最优的聚类参数，可提高分类器的泛化能力.

3 实验与分析

实验1 采用 UCI中的Japanese Vowels数据集.该数据被用来检验多维时间序列分类器的性能.分析对象为3个类别对应3个日本女性的元音发声，由12个LPC离散频谱系数指标描述每个话语的特征.训练样本总数为90个，每个类别30个样本.所选数据集96个样本分为3类，C1:31、C2:35、C3:30.使用以上数据验证时序分类器的有效性.

经训练和计算，确定网络结构参数选择如下:12个输入节点(对应12个LPC系数)，3个复合径向基过程神经元单元，输出层对应k个类别标记的节点，只有1个被激活.标准正交基函数取为勒让德多项式，基函数个数为6个;取12个LPC在连续时间点上的离散采样数据拟合为12个输入时变函数，作为网络的过程式输入.为提高网络的泛化能力，经多次分析比对，确定参数αi(0＜αi＜1)的值为0.09，0.116和0.113(多系数方法)，为进一步验证该算法的性能，依据相同的训练和测试样本，采用单一聚类系数(αi= 0.1，i=1，2，3)的网络输出对比结果如表1所示.

由表1可见，在多系数方法对训练样本的识别率略低于单系数方法的前提下，多系数方法对应的测试样本识别率高于单一系数方法的测试样本识别率，其原因在于相对于单一系数方法，多系数方法更加精确地调整了各聚类的大小，因此具有相对较高的测试样本识别正确率.可见，采用多系数方法提高了时序分类器的泛化性能.

实验2 应用与实验1相同的训练样本和测试样本，测试本文算法与文献［1］算法在相同样本下的分类正确率.本文算法与文献［1］算法对于96个测试样本的分类结果如图3和表2所示，文献［1］算法为比较算法.本文方法的测试样本的分类正确率为97.92%，文献［1］方法的测试样本分类正确率为90.625%.

图3 分类正确率比较Fig.3 Comparison of classification accuracy

表2 不同方法下的分类正确率Table 2 Classification accuracy of different methods

从图3及表2可见，本文算法的分类正确率高于文献［1］算法，其原因在于本文算法依据样本密度计算聚类中心及半径，改进了文献［1］的学习算法，并使用多系数方法调整各聚类的大小，针对每类样本的实际训练情况，依据样本到各聚类中心的距离，调整各聚类的中心宽度，提高了算法的分类正确率.

实验3 应用与实验1相同的训练和测试样本，测试本文算法与文献［1］算法在不同样本数量下的分类正确率.变换训练数据的数量，从90－800，测试两种算法的正确率(如图4所示)，文献［1］算法为比较算法.从中可见，本文算法在不同训练样本大小下的分类正确率均高于文献［1］算法，同时在该数据集上2个算法受训练样本数量影响不大，基本处于稳定水平，分析其原因在于，2种方法均属于应用领域知识的分类方法，因此，在各类样本能充分反映其分类特征且不存在过拟合的情况下，其对应的样本分类正确率相对稳定.

实验4 应用与实验1相同的训练样本和测试样本，测试本文算法与文献［1］算法在不同样本数量下的执行时间.变换训练数据的数量，从90～800，2种算法在不同训练样本数量下的运行时间如图5所示.从中可见，在不同训练样本数量下，本文算法的计算速度均高于文献［1］算法，其原因在于本文算法将时序分类的过程转化为过程式输入与核中心函数的比较距离测量问题，省去了所有径向基过程神经元输出线性连接权的计算，由复合竞争过程神经元单元完成对过程式输入信息的时空聚合和模式匹配工作，简化了网络结构和训练过程，因此本文算法在不同训练样本数量下的计算速度均高于文献［1］算法.

图4 训练样本大小对算法的影响Fig.4 The effect of training sample size on algorithm

图5 执行时间比较(仿真数据集)Fig.5 Comparison of runtime(synthetic dataset)

4 结束语

时间序列分类是时间序列数据分析中的重要任务之一，它比一般分类问题困难的原因在于待分类时序数据不等长的特征，使得一般的分类算法不能直接适用［3－10］.本文将径向基过程神经网络引入到时序分类中，对径向基过程神经网络进行改进，提出一种基于竞争型径向基过程神经网络的时序分类方法，简化了网络结构和训练过程，将时间累积效应纳入其中，同时突破了时序数据不等长的限制.实验结果表明，本文方法能够有效地提高时序分类正确率和泛化性能，并且随着训练样本数量的增加，本文算法在分类正确率和计算速度上均表现出很好的性能.

［1］许少华，何新贵.径向基过程神经元网络及其应用研究［J］.北京航天航空大学学报，2004，30(1):14-17.

XU Shaohua，HE Xingui.Research and applications of radial basis process neural networks［J］.Journal of Beijing University of Aeronautics and Astronautics，2004，30(1):14-17.

［2］黄国宏，刘刚.新的C2 RBF神经网络分类器的设计与实现［J］.计算机应用研究，2008，25(3):709-711.

HUANG Guohong，LIU Gang.Design and realization of new C2 RBF neural networks classifier［J］.Application Research of Computers，2008，25(3):709-711.

［3］RICARDO B C P，TERESA B L.A modal symbolic classifier for selecting time series models［J］.Pattern Recognition Letters，2004，25(8):911-921.

［4］杨一鸣，潘嵘，潘嘉林，等.时间序列分类问题的算法比较［J］.计算机学报，2007，30(8):1260-1265.

YANG Yiming，PAN Rong，PAN Jialin，et al.A comparative study on time series classification［J］.Chinese Journal of Computers，2007，30(8):1260-1265.

［5］KEOGH E，KASETTY S.On the need for time series data mining benchmarks:a survey and empirical demonstration［C］//Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.Edmonton，Canada，2002:102-111.

［6］JORGE C，NUNO C.A period gram-based metric for time series classification［J］.Computational Statistics＆Data A-nalysis，2006(50):2668-2684.

［7］WENG Xiaoping，SHEN Junyi.Classification of multivariate time series using locality preserving projections［J］.Knowledge-Based Systems，2008(21):581-587.

［8］ORSENIGO C，VERCELLIS C.Combining discrete SVM and fixed cardinality warping distances for multivariate time series classification［J］.Pattern Recognition，2010(43): 3787-3794.

［9］王晓晔，肖迎元，张德干.时间序列部分周期模式的更新算法［J］.哈尔滨工程大学学报，2011，32(11):1484-1488.

WANG Xiaoye，XIAO Yingyuan，ZHANG Degan.Partial periodic pattern updating technology in time series databases［J］.Journal of Harbin Engineering University，2011，32 (11):1484-1488.

［10］付永庆，宋宝森，吴建芳.边缘分类SIFT算法［J］.哈尔滨工程大学学报，2010，31(5):632-636.

FU Yongqing，SONG Baosen，WU Jianfang.An improved scale invariant feature transform algorithm［J］.Journal of Harbin Engineering University，2010，31(5):632-636.