弹体出水引起的非稳态流场数值计算方法
姚熊亮,张成,杨衡,张忠宇
(1.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001;2.中国舰船研究设计中心,湖北武汉430064)
流场处于非稳定状态往往是由于砰击作用引起的,自然界中存在各种各样的砰击现象.人们往往对某些显而易见的砰击现象感兴趣,如波浪载荷的砰击作用,但事实上很多常见的物理现象也可能产生瞬间的砰击作用,如弹体出水时,弹头与自由面撞击,就会产生一种砰击现象.砰击现象的特点是流场瞬间变化剧烈,瞬间的砰击作用引起的水动力非常大.这种砰击作用使结构周围流场在初始时刻附近处于不稳定状态,而这种非稳态流场的动压力值比稳态流场的动压力值大几倍甚至几十倍.另外水下爆炸冲击波载荷作用下的船体结构流固耦合问题也是以流场瞬间剧烈变化为特点,对船体结构造成非常强烈的冲击,进而导致非常严重的毁伤.但无论是强烈的冲击问题还是弱砰击问题,均是以流场瞬间剧烈变化为特点,解决这类问题的关键在于必须考虑流场可压缩性.
如今,解决如水下爆炸这样的强冲击问题有很多方法,著名的有延迟势法[1-2]、双渐近法(DAA)[3-6]等.这些方法能较为成功的应用于水下爆炸领域,因此一直被沿用至今.由于弹体出水砰击问题和水下爆炸问题均须考虑流场可压缩性,因此采用擅长解决水下爆炸问题的双渐近法,将其应用于弹体出水砰击问题.但该法存在局限性,即是基于线性化假设提出的一种理论[7],从理论上来说是不能用于分析航行态或做大幅运动结构的瞬态运动问题.弹体出水恰是典型的具有初始航速的瞬态运动问题,这样的流固耦合问题不但以“砰击”为主要特点,还有一重要特点即“非线性”.所以对弹体出水问题的分析,采用传统的双渐近法和不考虑可压缩性的势流理论方法均不适合.
针对双渐近法只能用于解决准静态条件下的流固作用的局限性,在DAA2法的基础上,将运动非线性引入双渐近法,提出改进方法,即非线性双渐近法(NDAA).使双渐近法可应用于航行态结构或做大幅运动结构的流固耦合问题.并以具有初始航速的弹体为例,采用两种方法(DAA2以及NDAA)捕捉弹体出水时可能会发生的砰击现象,模拟弹体砰击引起的非稳态流场.将NDAA与DAA2法的数值计算结果进行对比,分析考虑非线性效应的流场和弹体出水时可能会发生的物理现象.
1 非线性双渐近法(NDAA)
浸在水中的结构物与流场的瞬态耦合问题有这样的特点:早期瞬态(高频)响应主要是声辐射问题,即所谓平面波或曲面波近似解问题;后期瞬态(低频)响应主要是"虚质量"问题.用延迟势原理可分别得出其早期(高频)近似式(E.T.A)和后期(低频)近似式(L.T.A).Geers等(1975~1980),根据这些特点提出了双渐近法(DAA),就是用渐近展开匹配法导出能用于中间频率的微分方程式.当趋于高频时其解渐近于早期近似解(E.T.A);在低频时就渐近于后期近似解(L.T.A)[3].
双渐近法(DAA)之所以能广泛应用于水下爆炸领域,其中一个重要原因是它考虑了流体可压缩性,考虑可压缩性的势函数微分方程式:
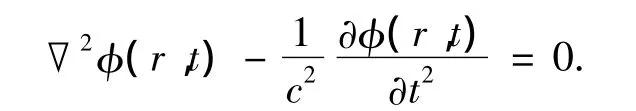
DAA法就是从上述控制方程的基础上经推导得到.DAA法的基本方程如下[4]:
一阶双渐近法方程(DAA1):
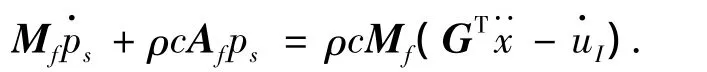
二阶双渐近法方程(DAA2):

结构动力方程:

式中:pS为流体中的散射压力,pi为入射波压力,Mf为流体质量矩阵,Ωf为流体频率矩阵,Af为流体单元的面积矩阵,uⅠ为入射波速度,x为结构位移,G为坐标转换矩阵.
Geer[5]在他的研究中指出,一阶双渐近法DAA1在高频时相当于平面波近似式(PWA),在低频时相当于虚质量近似式(VMA).二阶双渐近法DAA2在高频时相当于曲面波近似式(VWA),在低频时相当于修正的虚质量近似式(VMA)[5].
但无论对DAA1还是DAA2,在其理论推导的过程中,均引入了一个线性假设,即

式中:P=pS+pi,即总的流场动压力值,φ为流场速度势.
式(3)中压力P和速度势φ呈线性关系.对高频动载作用下结构做线性小扰动时的周围流场进行动压力计算,这种假设是合理的.因为速度势的空间导数本身就很小,其二次项就更小了,压力的线性项即速度势的时间导数比其空间导数大得多.因此,忽略速度势随空间的变化,认为速度势是时间的函数,这种情况下,对压力作线性假设是合理的.但水中结构物如果处于航行态或做大幅运动,其非线性效应对水动力值影响比较显著,速度势的空间导数就不能忽略了.为此,对DAA2法进行改进,将速度势的空间导数引入到DAA2法的数值计算,从而将非线性的影响考虑到水中结构物的瞬态流固耦合计算当中.
DAA2法是从延迟势法基础上得到,延迟势的速度势方程如下:

将式(3)代入式(4),可得延迟势的压力方程:

DAA1方程和DAA2方程均是在延迟势压力方程式(5)的基础上得到,也就是说,DAA1方程和DAA2方程是在经过式(3)线性变换的情况下得到的.
求解DAA方程式(1),相当于求解式(5),在通过DAA2方程式(1)的求解可以得到流场散射压力ps,即延迟势方程式(5)中的ps.
由式(3)可得
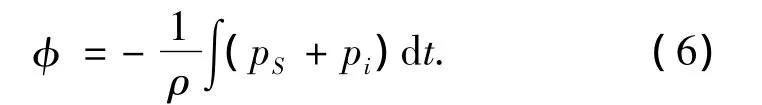
式(6)中的流场散射压力pS通过求解DAA方程式(1)得到,入射波压力pi作为已知条件,那流场总速度势φ即可得解.
在得到流场速度势的基础上,可以通过伯努利方程得到流场动压力计为Pd:

式中:V为结构运动速度.
解式(8)得到的流场动压力值与解DAA2方程得到的流场动压力值的本质区别在于式(8)中的第2项和第3项,式(8)中的第2项仍是线性项,但考虑了结构的航速效应,第3项是非线性项,考虑了结构的运动非线性.
求解式(8)得到考虑非线性效应的流场动压力,将该考虑非线性效应的流场动压力ps+pi代入结构运动方程中,于是式(2)可写成如下形式:
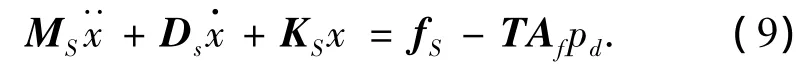
将式(6)、(8)、(9)与DAA2方程(1)联立求解的方法称为NDAA法.
采用三角形单元对结构进行离散,如图1所示.在对式(8)的求解中,需要对速度势方向导数▽φ进行求解,求解思路如下[8]

式中:符号j表示第j个三角形单元,A、B、C表示一个三角形单元的3个节点,x、y、z表示直角坐标系下的坐标,n表示单位法向矢量.
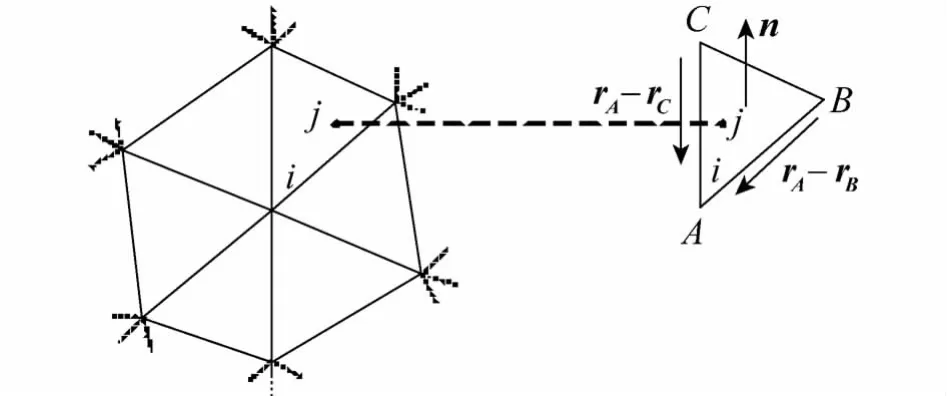
图1 节点i及周围单元,j表示其中的一个单元Fig.1 Node i and its surrounding elements,j is element number
通过对式(10)的求解,就可以得到单元j的速度势梯度▽φ了,其他单元类同.注意这里用(uj,vj,wj)代替▽φ.
2 弹体出水引起的非稳态流场数值模拟
考虑导弹从自由面以下一定深度处以一轴向初速度做出水运动,在弹体横向存在一定横向初速度,除受流场动压力以外,不受其他任何外力作用.研究弹体在出水过程中其周围流场各节点动压力值的变化,并将流场动压力P、时间T、结构运动速度V无量纲化.
无量纲结点运动速度为

无量纲流场动压力为

无量纲时间为

式中:V0为弹体初始运动速度,l0为初始时刻弹体顶点距自由液面的距离.
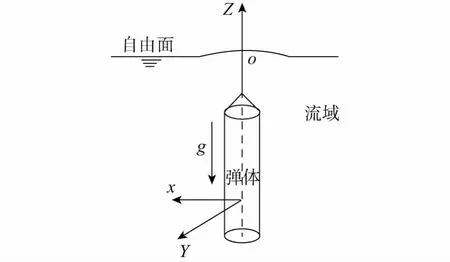
图2 物理模型Fig.2 Physical model
2.1 非稳态流场时间分布
本节从时间的角度分析弹体各点流场动压力,分析弹体出水过程中流场动压力的变化、非线性效应不能被忽略的流场状态以及弹体出水时可能会发生的物理现象.
图3给出了2幅相互对应的图,第1幅表示弹体顶点流场动压力,第2幅表示弹体顶点垂向速度.2幅图在各个时间段都一一对应.弹体顶点出水前,其流场动压力以及垂向速度均是从高频非稳态区线性过渡到低频稳态区;弹体顶点出水后,弹体顶点作为结构的一部分,仍然存在垂向速度,但此时该点已位于空气中,流场动压力为0.
另外在如图3所示的非稳态区,流场动压力极大.非线性双渐近法NDAA和二阶双渐近法DAA2的数值计算结果很接近,即对于高频非稳态区,非线性效应不明显.在稳态区,流场动压力相对较小,非线性双渐近法NDAA比二阶双渐近法DAA2的数值计算结果偏大,即对于低频稳态区的流场,非线性效应显著.另外从图3中还可以看出,t=0.4是流场非稳态区和稳态区的分界线.
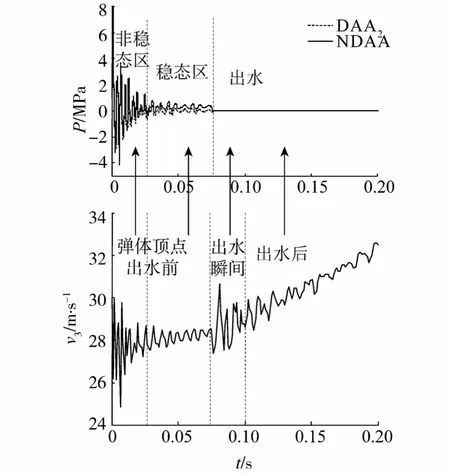
图3 弹体顶点压力及其垂向速度时历曲线Fig.3 The pressure-time curve and the velocity-time curve of the top node of the missile
稳态区所对应的结构垂向速度也趋于稳定状态,垂向速度V平均值大概0.94左右.如果按不考虑可压缩性的势流理论的观点,弹体以垂向速度在水中做匀速运动(忽略横向速度对弹体顶点压力的影响),弹体顶点的理论压力值大概在0.896附近.值得注意的是,采用NDAA法,稳态区的压力平均值大概在0.95左右,采用DAA2法,稳定后的压力平均值在0附近.可见,DAA2法虽然理论上在结构运动后期趋于势流理论中的虚质量假设,但是由于它没有考虑运动非线性,在后期处理有初始航速的结构时,其数值计算结果是与势流理论解不符.而NDAA法不但在前期与DAA2法结果符合良好,能较好的反映非稳态流场的本质特征,而且在后期趋于势流理论中的虚质量假设,能较好的反映稳态流场的物理特性.
该节点位于弹体头部与中部交界处,弹体顶点于t=1.1时开始出水.而该节点此时还未露出水面,但也明显受到弹体顶点出水的影响,在其压力时历曲线上可以观察到2个较为明显的压力峰值,即双峰值.该节点在t=1.5以后出水,出水后流场压力降为0.如图4所示.
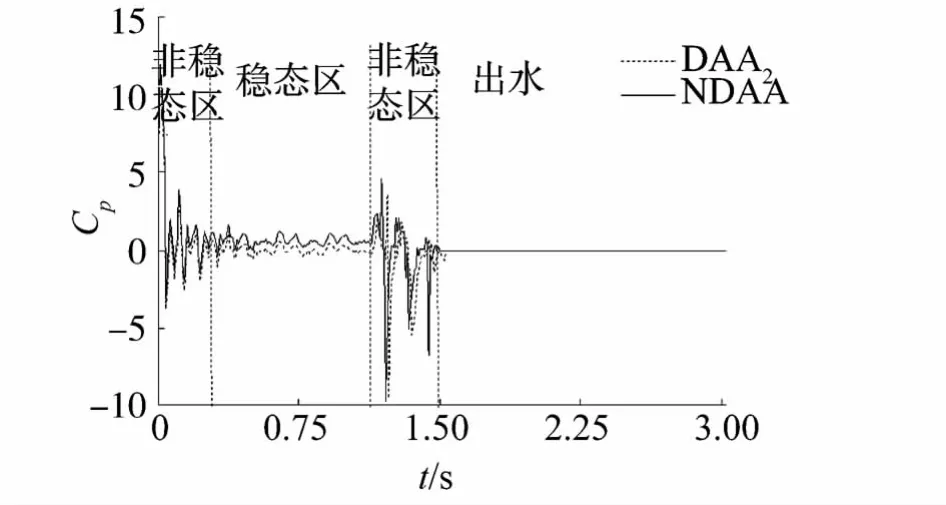
图4 弹体头部与中部交界处某点压力时历曲线Fig.4 The pressure-time curve on the shoulder of the missile
该节点反映了弹体头部的压力变化特征,经历非稳态、稳态、再到非稳态这样一个过程.第1个非稳态是由瞬间初速度产生的砰击而引起的,第2个非稳态是由弹头与自由面砰击而引起的.可以从该点的压力曲线上观察到第1个非稳态对应的稳态过程,无法观察到第2个非稳态对应的稳态过程.说明弹头出水时会使流场一直处于非稳定状态,直至整个弹头均露出水面.
另外,和弹体顶点类似,非线性效应对非稳态区流场动压力值影响微弱,对稳态流场动压力值影响显著.稳态区流场动压力平均值的NDAA法数值计算结果在0.85左右,DAA2法的数值计算结果在0左右.
图5所示节点位于弹体中部距弹体肩部1/4弹体长度的地方.该节点虽然没有布置在弹体头部,但其压力值明显受到了弹头出水的影响.弹头出水时,和图4类似,在其压力时历曲线上也可以观察到双峰值现象.由于没有对双峰值的产生机理做深入探讨,初步判断,双峰值可能是由弹头形状引起的.因为弹头出水的时间恰好是双峰值产生的时间,并且弹头形状近似三角形,三角形结构属斜壁出水而非直壁出水,斜壁浮体的大幅运动问题现在也正是水动力学的重要难点.
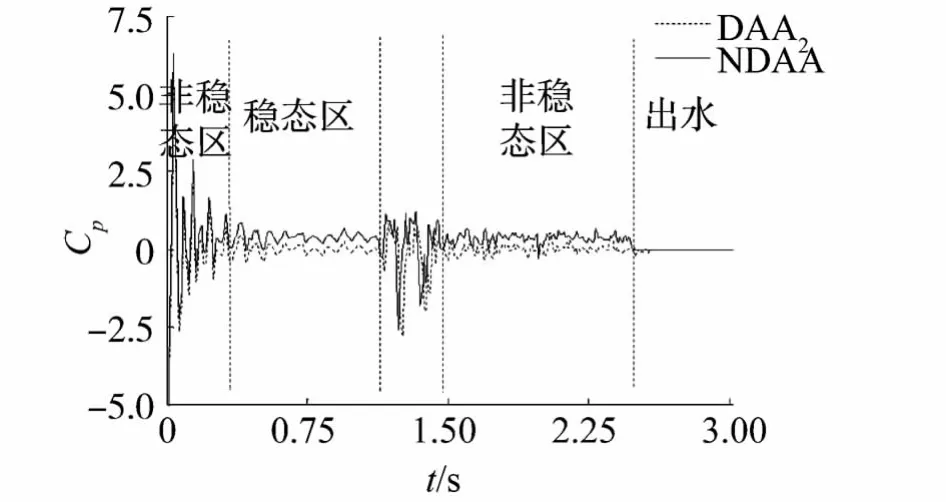
图5 弹体中部压力时历曲线Fig.5 The pressure-time curve on the middle of the missile
该节点流场动压力主要经历4个阶段,即非稳态、稳态、非稳态、稳态.2个非稳态区的产生机理和图4类似,不再赘述.第2个稳态区对应的是弹体中间的圆柱部分出水,而弹体中间圆柱部分出水属直壁出水,这意味着结构直壁出水时不会产生砰击现象.
由图6可以看出,弹体尾部节点压力值比其他节点都稍大,稳定值在0.98左右.尾部节点压力曲线存在有趣而且特殊的物理现象,即其曲线存在显著的拍振特征.大概是3个周期1个拍,拍振发生的前提条件存在2种相近的频率特征.对于弹体来说,这2种频率可能来源于弹体尾部的局部振动以及流场动压力频率,而这2种频率又接近,导致拍振的发生.这就意味着弹体某些局部结构可能会发拍振现象.拍振现象的发生可能导致弹体局部结构振幅很大,振动强烈,进而导致结构破坏.

图6 弹体尾部压力时历曲线Fig.6 the pressure-time curve on the bottom of the missile
总结图3~6,弹体出水需经历4个阶段,即非稳态、稳态、非稳态、稳态这4个过程,如图7所示.

图7 弹体出水时流场物理特性变化过程及其成因Fig.7 Changing process of the fluid characters andthe causes at missiles flying out of the water surface
2.2 非稳态流场空间分布
针对不同阶段的流场动态特性,取分别表征4个流场状态(非稳态、稳态、非稳态、稳态)的4个特征时间点(初始时刻附近,t=0.45;出水前,t=0.9;出水瞬间,t=1.27;出水后,t=3).采用非线性双渐近法(NDAA)对弹体周围流场动压力的空间分布做详细分析.
将弹体中间圆柱部分沿轴线从中间切开,展开成矩形,图8、9给出了弹体中间圆柱部分周围流场动压力沿弹体轴向和周向的分布情况.用(X、Y、Z)分别表示弹体各点轴向、横向、法向坐标,坐标原点位于弹体顶点,并且轴向正方向指向弹体尾部,L表示弹体长度,R表示弹体中间圆柱部分的最大半径,θ表示弹体中间圆柱部分的周向角度,θ=0对应弹体横向迎流面的中线.

图8 非稳态流场(t=0.45)与稳态流场(t=0.9)对比Fig.8 Comparison between unsteady flow field(t= 0.03 s)and the steady flow field(t=0.06 s)

图9 非稳态流场(t=1.27)与稳态流场(t=3)对比Fig.9 Comparison between unsteady flow field(t= 1.27)and the steady flow field(t=3)
无论是弹体初始速度引起的非稳态流场,还是弹头出水时与自由面砰击而产生的非稳态流场,水动压力值均比对应的稳态流场压力值大得多.非稳态流场动压力值沿空间的分布也相对复杂,尤其是沿弹体轴向.弹体属细长体,轴向受力不均容易使弹体产生较大的弯矩,进而导致弹体折断,说明非稳态流场数值模拟十分必要.
另外在初始时刻附近,可以观察到较为明显的低压区(见图10),分布在弹体肩部附近.低压区的压力极小,很可能在弹体肩部形成空化现象[9],即产生空泡,空泡区域的大小跟弹体周围压力的分布以及空化压力有关[10-11].在出水瞬间,低压区开始下移即空泡区下移,也就是说,弹体出水可能导致空泡形成的区域以及位置发生改变.如果空化压力确定以后,可以通过流动压力的空间分布来预测空泡区域的大小及其分布位置.这里不对弹体的空化现象做深入讨论.

图10 流场动压力沿弹体轴向分布(θ(2π)=0)Fig.10 Dynamic pressure along the axial direction (θ(2π)=0)
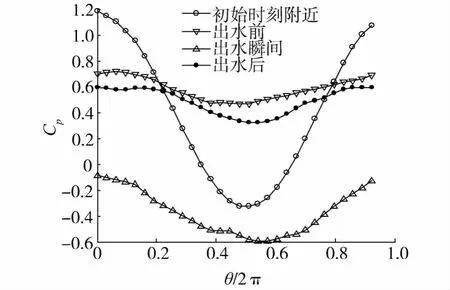
图11 流场动压力沿弹体周向分布(X/L=0.5)Fig.11 Dynamic pressure along the circumferential direction(X/L=0.5)
低压区即空泡区下移也可以从流场动压力沿轴向分布图中看出来(见图11).初始时刻的流场动压力比出水瞬间流场动压力稍大,也就是说,弹体瞬间初速度引起的砰击比弹头出水引起的砰击要强烈.但二者均比各自对应的稳态流场压力大得多,出水前的稳态流场压力比出水后稍大.弹体压力沿周向分布较规律,接近正余弦分布,尤其是初始时刻附近,流场动压力沿轴向基本呈均值为0的余弦分布.
由图12可以看出,初始时刻附近弹体头部流场动压力关于轴线呈对称分布.横向运动几乎不对头部压力分布造成影响,对头部压力主要造成影响的是垂向运动.因为在弹体垂向,弹体突然以某一初速度出水.而弹体头部恰好是迎流面,从而产生剧烈的砰击,流场处于不稳定状态,导致弹体头部流场动压力值极大.t=0.45的弹头压力系数最大值可达到5.5.如果按不考虑可压缩性的势流理论的观点,弹体以某一初速度在水中做匀速运动,弹体顶点的压力系数大概在1左右.可见,如果采用不考虑可压缩性的势流理论方法,是无法对这种高频高幅非稳态流场进行数值模拟的.

图12 初始时刻附近(t=0.45)弹体头部流场动压力Fig.12 The hydrodynamic on the head of the missile at the beginning(t=0.45)

图13 出水前(t=0.9)弹体头部流场动压力Fig.13 The hydrodynamic on the front part of the missile before flying out of the water surface(t=0.9)
由图13可以看出,出水前弹体头部稳态流场关于轴线呈非对称分布,关于横向对称.这是因为流场处于稳定状态时,弹体头部的砰击影响越来越微弱,可压缩性影响越来越小,流场动压力分布越来越趋于势流理论解.从图中还可以看出,弹体头部压力场分布是横向速度和垂向速度共同作用的结果,这与势流理论解是一致的.这也说明非线性双渐近法在后期趋于势流理论的虚质量假设.
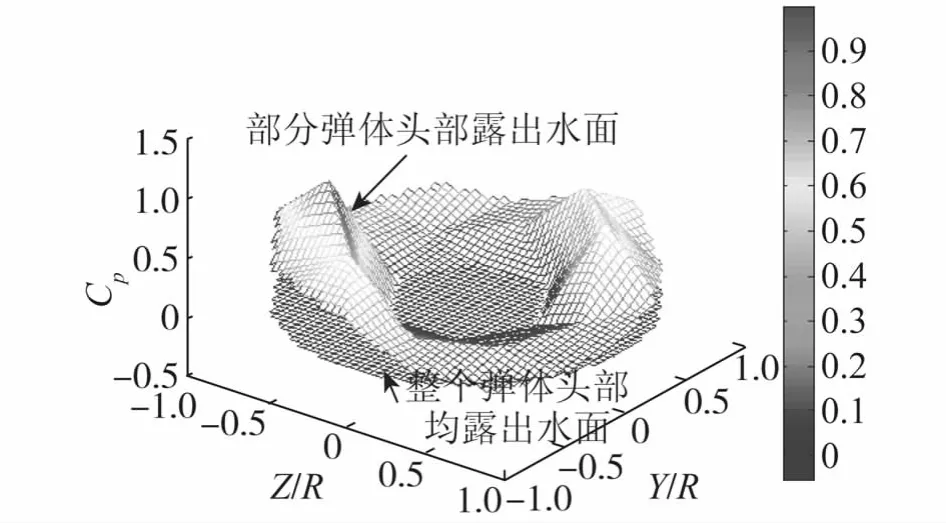
图14 出水瞬间(t=1.27)和出水后(t=3)弹体头部流场动压力Fig.14 The hydrodynamic on the front part of the missile when flying out of the water surface(t=3)
图14为部分弹头出水,出水部分压力为0,未出水部分压力很大.而部分弹头出水,正是砰击较为强烈的时刻,整个弹头出水后,砰击现象也就消失了,说明只有弹头部分与自由面产生砰击作用.弹体中间的圆柱部分出水时,不会产生砰击现象.
3 结论
在DAA2法的基础上,将运动非线性引入双渐近法,即非线性双渐进法(NDAA),比较了两种方法的数值计算结果,分析非线性对弹体出水流固耦合动态特性的影响.简单探讨了弹体出水时双峰值的产生机理以及弹体出水时其局部结构可能会发生拍振的现象.探讨了非稳态流场的成因,给出了不同阶段的流场动态特性,以及各个特征时间点流场动压力的空间分布情况.得到主要结论如下:
1)在非稳态区,流场动压力极大,非线性效应不明显;在稳态区,非线性效应显著.对于具有一定初始航速的结构,如弹体出水的流固耦合问题,应该考虑非线性效应.
2)弹体出水过程中可观察到砰击现象,第1次砰击发生在弹体以某一初速度瞬间启动时,第2次砰击发生在弹头出水时.砰击时,弹体周围流场处于不稳定状态.弹体整个出水过程可以概括成4个物理状态,即非稳态、稳态、非稳态、稳态.非稳态流场动压力值比稳态流场大得多.
3)NDAA法在前期与双渐近法结果符合良好,能较好的反映非稳态流场的本质特征,在后期趋于势流理论中的虚质量假设,能较好的反映稳态流场的物理特性.
4)在研究弹体出水过程中还观察到了2个重要的物理现象:一是双峰值现象,二是拍振现象.
5)弹体未出水时,弹体周围低压区位于弹体肩部,这可能是肩空泡产生的原因.随着弹体头部开始出水,低压区开始下移,这可能导致空泡区下移.
[1]HUANG H.Transient interaction of plane acoustic waves with a spherical elastic shell[J].J Acoust Soc Amer, 1969,45:661-670.
[2]DYKA C T,INGEL R P.Transient fluid-structure interaction in naval applications using the retarded potential method[J].Engineering Analysis with Boundary Elements,1998,21:245-251.
[3]GEERS T L.Residual potential and approximation methods for three dimensional fluid-structure interaction problems[J].J Acoust Soc Amer,1971,49:1505-1510.
[4]GEERS T L.Doubly asympotic approximation for transient motions of submerged structures[J].J Acoust Soc Ame,1978,64:1500-1508.
[5]GEERS T L,FELIPPA C A.Doubly asymptotic approximations for vibration analysis of submerged structures[J].J Acoust Soc Amer,1980,73:1152-1159.
[6]GEERS T L,ZHANG Peizhane.Advanced DAA methods for shock response analysis[R].Denver:University of Colorado,1992:252-696.
[7]SPRAGUE M A,GEERS T L.Response of empty and fluidfilled submerged spherical shells to plane and spherical,step-exponential acoustic waves[J].Shock and Vibration,1999(6):147-157.
[8]ZHANG Aman,YAO Xiongliang.The interaction between multiple bubbles and free surface[J].Chinese Physics B,2008,17(3):927-938.
[9]权晓波,魏海鹏.潜射导弹大攻角空化流动特性计算研究[J].宇航学报,2008,29(6):1701-1705.
QUAN Xiaobo,WEI Haipeng.Numerical simulation on cavitation of submarine launched missile's surface at large angles of attack[J].Journal of Astronautics,2008,29 (6):1701-1705.
[10]罗金玲,毛鸿羽.导弹出水过程中气/水动力学的研究[J].战术导弹技术,2004,7(4):23-25.
LUO Jinling,MAO Hongyu.Research on aerodynamics and hydrodynamics in exiting water process of missile[J].Tactical Missile Technology,2004,7(4):23-25.
[11]REN Bing,LI Xuelin,WANG Yongxue.Experimental investigation of instantaneous properties of wave slamming on the plate[J].China Ocean Engineering,2007,21(3): 533-540.

