悖论与解决交通拥挤的经济学方法有效性

何胜学

（上海理工大学管理学院，上海 200093）

交通问题不是一个简单的工程问题，而是一个复杂的系统问题.单纯发展交通基础设施建设不可能解决目前我国交通存在的负外部性问题.目前我国交通基础设施建设已经进入了一个高速发展期.高铁、动车、磁悬浮以及快速扩展的高速公路网，已成为人们日常生活的一部分，但是相应的交通负外部性问题也日益突出.不仅在2010年广州亚运会和2008年北京奥运会这样的特殊时期，交通管理部门需要采取单双号限行、城市局部区域交通管制以及限制外省市车辆进入的方法来缓解城市交通压力；即使在平日，大城市公共交通和地面道路交通也相当拥挤.区域高速公路上不时出现的绵延千里的排队车辆和时不时由于恶劣天气导致的局部运输瘫痪，也说明当前的区域运输面临严峻考验.

对于这样一个复杂的交通问题，人们提出了许多不同的解决方案.一些交通工程专家认为加大基础设施建设，并引入新技术可以解决问题.不断增加的公路网密度、拓宽的道路、智能交通系统的推广，正是实践着这一观点.一些经济学家觉得只有对准公共物品，如交通基础设施和相应的环境资源，实施混合产权，进行拥挤收费，才能有效地解决上述问题.西方的一些国家在这方面已进行了不少实践.普通老百姓则觉得人太多、车太多以及油太贵才是问题关键.

只有进行长期的深入研究，才能有效实现普通老百姓、学者专家和政府间的协调一致，共同实现交通系统的可持续健康发展.本文尝试利用两个简单的悖论，揭示各方观点的合理性与局限性；说明只有通过多方的共同努力，审慎地采取可行方法，才能有效地降低交通系统的负外部性影响.

1 Braess悖论与路径选择行为

图1是Braess悖论路网.图1中有5条路段和1个OD对（origin－destination pair）.用ti表示通过路段i的行程时间，xi表示通过路段i的交通量.图1中的路段行程时间函数分别为t1＝50＋x1，t2＝50＋x2，t3＝10x3，t4＝10x4和t5＝10＋x5.OD对（1，4）间总的交通需求量为d14＝6.在图1中，连接OD对有3条路径.路径1包含路段1和4；路径2包含路段3和2；路径3包含路段3、5和4.路径k上的流量和总行程时间分别用fk和ck表示.

假设出行者均从自身利益角度出发，寻找使自己旅行时间最小的路径出行，且每个出行者独立作出决策，并具有路网的完全信息.当没有人可以通过单方面的改变出行路径缩短自身的旅行时间时，称此时的网络处于用户均衡状态，即满足Wardrop第一原则［1－6］.

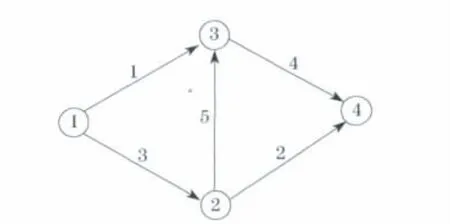
图1 Braess悖论网络Fig.1 Network of Braess Paradox

分两种情形分析图1中的路网状态.第一种情形假设路段5还未修建，即用户不能使用路段5.此情形下，当网络处于用户均衡时，路径流量为f1＝f2＝3，路径的行程时间为c1＝c2＝83.此时，网络的总旅行时间为498.第二种情形下，用户可以利用路段5.当网络处于用户均衡时，路径流量为f1＝f2＝f3＝2，路径的行程时间为c1＝c2＝c3＝92.此时，网络的总旅行时间为552.两种情形相比，增加新路段的使用反而使出行者个体和系统整体的境况变糟.这一诡异现象揭示了不考虑出行者行为模式，单纯地增扩路网不一定能改善系统运行状态.

显然，假设出行者服从Wardrop第二原则［1－2］，即系统最优原则——选择出行路径使得网络的总旅行时间最小，路网的最终状态为f1＝f2＝3，f3＝0，c1＝c2＝83和c3＝70.此时，网络的总旅行时间为498.但是出行者个体是不会自觉遵循上述原则的，因此交通管理部门要么关闭路段5，要么采取其它的措施，如拥挤收费或发放通行许可证等.

假设用户可以使用路段5，下面从一个全新的角度看看普通百姓对拥挤形成的观点是不是也可以用上面的路网加以验证.先设OD对间的出行需求减少为d14＝3，易得所有出行者均将选择路径3出行，此时，c1＝c2＝80和c3＝73.如果假设OD对间的出行需求增加为d14＝30，易得将各有一半的出行者分别选择路径1和路径2出行，而没有出行者选择路径3，此时，c1＝c2＝215和c3＝300.综上可知，当总的交通需求量较小时，出行者仅会使用路径3，增加路段5是有益的；而当需求量进一步增大时，如d14＝6，3条路径均会被使用，增加路段5反而有损系统和出行者个体的效益；当需求量进一步增加，如d14＝30，出行者会放弃选择路径3，因此增加路段5，对系统无影响.随需求量增大而不断增大的实际使用路径行程时间，说明了普通百姓观点的正确性；同时这一新的观察视角也出人意料地表明，悖论的出现与总的网络出行需求大小紧密相关.

Braess悖论说明交通问题不仅是一个工程问题，也是一个行为科学问题.但是这样的一个单OD对路网还不能揭示涉及多OD对时交通管理的复杂性和管理措施的社会公平性问题.

2 Lovell悖论

图2是Lovell悖论网络扩建前后的示意图.前期的网络由连接两个OD对的两条路段组成.OD对间的交通需求量为d13＝2和d24＝3.扩建后路网新增了路段3、4、5、6和7.路段的行程时间函数为t1＝2，t2＝3，t3＝0，t4＝0，t6＝0，t7＝0和t5＝x5.上述路段行程时间函数表明在现有交通需求下，除路段5具有拥挤特征外，其他路段均具有固定的通行时间.当然通行时间为0仅是对实际情况的近似，表明实际的路段通行时间相比较而言可以忽略.扩建后，连接OD对（1，3）的路径有两条，其中路径1包含路段1，路径2包含路段3、5和6.连接OD对（2，4）的路径也有两条，其中路径3包含路段4、5和7，路径4包含路段2.

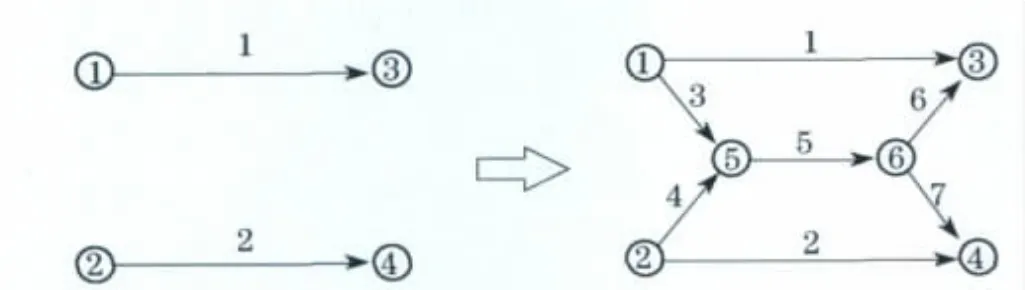
图2 Lovell悖论网络Fig.2 Network of lovell paradox

与分析Braess悖论一样，假设出行者遵循Wardrop第一原则，计算路网扩建前后网络处于用户均衡时的流量模式.显然，扩建前有f1＝2，f4＝3，c1＝2和c4＝3，总的网络出行时间为13.路网扩建后，各路径的流量为f1＝2，f2＝0，f3＝3和f4＝0.路网扩建后，各路径的行程时间为c1＝2和c2＝c3＝c4＝3.此时，总的网络出行时间仍为13.计算结果表明路网扩建后，部分出行者改变了出行路径，但是网络和用户个体的效益均没有改变.如果考虑到网络的连通性，OD对（1，3）间的出行者可能会尝试选择路径2出行，那么网络的状态将变得更糟.Lovell悖论是第一个针对多OD对情形的交通悖论，表明单纯的路网扩建不一定能改善网络的通行状况.

但是与Braess悖论不同，多OD对的Lovell悖论网络提供了出行状况改进的契机.计算系统最优条件下网络的均衡状态，各路径的流量为f1＝2，f2＝0和f3＝f4＝1.5.此时，各路径的行程时间为c1＝2、c2＝c3＝1.5和c4＝3，总的网络出行时间为10.75.但是交通管理者如何使得路网的流量变成上述系统最优的状态呢？下一节分析交通管理者可以采取的两种经济学手段.

3 解决拥挤的经济手段的有效性

交通管理者可以采取的缓解交通拥挤的两种经济学手段是交通拥挤收费（congestion pricing，CP）［7－8］和可交易瓶颈许可证（tradable bottleneck permits，TBP）［8－12］.而TBP在一些文献中又被称为可交易通行权（tradable driving right，TDR）［8］.在完全信息条件下，假设所有的出行者具有相同的时间价值观，则可以证明CP和TBP的实施效果是一样的.CP和TBP有很多具体的分类，下文仅对两者最常用的一般的形式进行分析.

首先，基于Lovell悖论分析以实现系统最优为目标的CP的实施效果.假设网络中所有的出行者的时间价值系数均为1，即收费值为1等价于增加的行程时间也为1.管理部门可以向通过路段5的所有出行者收取大小为1.5的费用，引导出行者选择合理的路径出行.OD对（2，4）间将恰好有1.5的流量选择路径3.此时，整个系统将达到系统最优条件下网络均衡状态.

可分析到此远没有结束，第一个问题是管理者如何确定收费的具体值大小.如果收费为0.5或2时，在所有的出行者的时间价值系数均为1时，系统不会平衡于系统最优状态.第二个问题是所有出行者不可能具有同样的时间价值系数，那么此时系统会如何变化.显然，如果收费为1.5，那么在OD对（1，3）间认为选择路径2的实际通行费用（行程时间转化的费用加上拥挤收费）小于选择路径1的行程时间费用的用户会选择路径2出行；同理，在OD对（2，4）间认为选择路径3的实际通行费用（行程时间转化的费用加上拥挤收费）小于选择路径4的行程时间费用的用户会选择路径3出行.这样使用路段5的出行者均是时间价值相对较高的出行者.从社会公平的角度看，那些时间价值相对较低的出行者（一般是收入较低者）因此不能使用新修的道路合理吗？同时这种情况下管理者根本无法预知谁会使用路段5和有多少出行者会使用路段5.结果是拥挤收费可能根本无法诱导网络达到系统最优状态.

那么现实中为什么管理者热衷于实施CP呢？第一个原因是目前的技术手段使得实施CP方便可行.交通专用短程通信（dedicated short range communication，DSRC）系统的应用和简单的费率设定使得CP成为一种实用的交通需求管理手段.第二个原因是管理者可轻易地增加收益.尽管交通管理者不愿意多提及该方面.

与CP从控制交通负外部性“质”的角度出发不同，TBP从“量”的角度出发实施对交通负外部性的控制［8－12］.可交易指的是许可证可以通过市场自由买卖.以Lovell悖论为例，交通管理部门将向市场投放数量为1.5的路段5的通行许可证.只有持有许可证才能通过路段5.如果许可证限制为OD对（2，4）间的出行者持有，则网络可以达到系统最优状态.

与CP相比，管理者可以通过限制TBP的持有人资格和数量，有效地控制网络的流量分布.TBP的市场投放可以采取网络平台拍卖的方式，也可以作为福利免费在使用者中发放.前一方式管理者可以得到收益，后一方式使得收益在用户中分配.因此，与CP相比，TBP的实施会得到更多公众的理解和支持.

可是与大量的CP的研究和实践相比，为什么TBP的研究和实践都较少呢？主要的原因是实施TBP，除了建立与CP相似的道边TBP识别管理系统外，管理者还需要做更多工作，包括建立TBP的网络拍卖市场，对使用者做前期的分析调查.同时，TBP系统还没有较好的办法处理一些意外情况，如交通事故导致的TBP失效和陌生的外地驾驶员的意外驶入等.实施成本和可能带来的收益的不确定性使得管理者对TBP抱更多怀疑态度.

最后，看看路段的最大通行能力限制对上述分析的影响.在扩建后的Lovell悖论路网中，假设路段5存在最大通行能力约束x5≤C5，这里C5是路段5的最大通行能力.如果C5的值大于3，易知原有的分析不变.在没有实施CP和TBP的情况下，如果2≤C5＜3时，由于在现有路段行程时间函数下路径3的行程时间一定小于路径4的行程时间，因此OD对（2，4）间的出行者趋于选择路径3出行，从而导致交通网络系统的不稳定，路段5的通行时间会急剧增大.但是此时路径2的行程时间一般保持大于路径1的行程时间，因此OD对（1，3）间出行者只会选择路径1出行.但是当1.5≤C5＜2时，系统会更加不稳定，出行者均趋向于选择通过路段5.当C5＜1.5时，原有的系统最优状态也不可能达到.

从“量”的角度出发控制交通负外部性的TBP能较好地适应上述路段通行能力的变化.但是此时对如何实施CP存在分歧.如果是以实现系统最优状态为目的，前面的对拥挤收费实施的分析没有大的变化.但是理论界对于应于何时实施CP有一种主流的看法是仅当路段会发生拥堵时实施.在最大通行能力内，路段5的行程时间是线性的，因此据此看法，只有当流量达到最大通行能力时，才可实施CP.但是从上一段的分析可以看出，许多情况下，系统即使没有出现拥堵，但是仍处于非常不稳定的状态.因此，主流观点是仅当路段会发生拥堵时实施CP会存在很大的实施隐患.

4 结束语

通过两个悖论，从不同角度深入分析了交通问题的复杂本质.交通问题不仅仅是一个交通工程问题，也是一个网络科学问题、行为科学问题、经济学问题、管理学问题和系统科学问题.解决交通问题不仅仅是交通管理部门的事，还需要普通民众的积极参与、社会方方面面的理解与支持以及学者专家的合作研究.

解决交通负外部性的一些经济学手段，并不像过去普遍认为得那么有效.如简单易行的拥挤收费并不代表一定有好的实施效果.在实施CP时，只有兼顾社会公平，并处理好成本与收益的关系，才能得到民众支持.同样对于准公共物品的管理，政府管理部门应当丢弃过于功利的想法，放眼长远的社会利益，重视前期的研究投入，如加大对如何实施TBP的研究的支持力度.通过分析，可以看出解决交通负外部性的经济学手段只有在利益各方的共同协作和支持下，从系统的角度出发，考虑社会经济的长期的发展，才能发挥其效用.

［1］ Nagurney A，Dong J.Supernetworks：decision－making for the information age［M］.Northampton：Edward Elgar，2002.

［2］ He S X，Fan B Q.Generalized wardrop principle and its application in regional transportation［J］.Transportation Research Record，2008，2085：49－56.

［3］ Yang H，Bell M G H.A capacity paradox in networkdesign and how to avoid it［J］.Transportation Research A，1998，32（7）：539－545.

［4］ Pas E I，Principio S L.Braess’paradox：some new insights［J］.Transportation Research B，1997，31（3）：265－276.

［5］ Ana L C，Bazzan A，Franziska K.Case studies on the Braess paradox：simulating route recommendation and learning in abstract and microscopic models［J］.Transportation Research C，2005，13（4）：299－319.

［6］ Roughgarden T.On the severity of Braess’s paradox：designing networks for selfish users is hard［J］.Journal of Computer and System Sciences，2006，72（5）：922－953.

［7］ Yang H，Huang H J.The multi－class，multi－criteria traffic network equilibrium and systems optimum problem［J］.Transportation Research B，2004，38（1）：1－15.

［8］ Ison S，Rye T.The implementation and effectiveness of transport demand management measures［M］.Aldershot，Hampshire，England：Ashgate Publishing Limited，2008.

［9］ Akamatsu T，Sato S，Nguyen X L.Tradable time－ofday bottleneck permits for morning commuters［J］.JSCE Journal of Infrastructure Planning and Management，2006，62（4）：605－620.

［10］ Akamatsu T.A system of tradable bottleneck permits for general networks［J］.JSCE Journal of Infrastructure Planning and Management，2007，63（3）：287－301.

［11］ Kikuchi S，Akamatsu T.Dynamics of decentralized multi－agent systems for implementing tradable network permits［J］.Infrastructure Planning Review，2008，25（3）：589－596.

［12］ Wada K，Akamatsu T，Kikuchi S.Convergence of dayto－day traffic flow dynamics under tradable bottleneck permits［J］.Urban Transport，2008，101（14）：579－588.