亚纯函数及其k阶导数权分担两个公共值的唯一性
张凤丽, 王新利
(上海理工大学理学院,上海 200093)
1 知识背景
亚纯函数是指在复平面CC上亚纯.对于任意非常数亚纯函数f,使用Nevanlinna值分布论中的基本结果及标准记号[1],如T(r,f),N(r,f),m(r,f),(r,f)等,特别地,用S(r,f)表示满足S(r,f)=o(T(r,f))(r→∞,r∉E,mesE<+∞)的量.对任意的两个复数a1,a2∈CC∪∞,若f-a1与g-a2的零点相同,并且每个零点的重数也相同,则称f与gCM分担(a1,a2)(若ai=∞,f-ai的零点就是f的极点);若不计重数,则称f与g的IM分担(a1,a2);若a1=a2=a,则称f与gCM(IM)分担a.
Gundersen[2]证明了f和f′CM分担两个公共值的唯一性,其结论如下:
定理1 设f是一个非常数亚纯函数,b(≠0)是一个有穷值.如果f和f′CM分担0和b,那么f≡f′.
Frank等[3]推广了上述结果,证明了f和f(k)关于分担公共值的如下性质:
定理2 设f是一个非常数亚纯函数,k(≥2)是一个整数,(a1,a2)和(b1,b2)是两对有穷值,满足a1≠b1,a2≠b2并且a2b2≠0.如果f和f(k)CM分担(a1,a2)和(b1,b2),那么,有
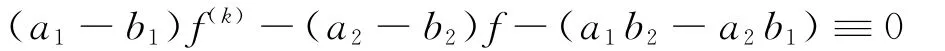
事实上,如果在上述定理中,设a1=a2=a,b1=b2=b并且ab≠0,那么即是下面的定理:
定理3 设f是一个非常数亚纯函数.如果f和f(k)CM分担两个不同的有穷非零复数a和b,那么f≡f(k).
Frank等[4]证明了如果f和f(k)CM分担任意有穷复数a和b,仍有f≡f(k)成立.后来Frank猜想,能否将条件“f和f(k)CM分担b”减弱为“f和f(k)IM分担b”,但仍有f≡f(k)的结论成立.李平[5]给出了如下的例子,证明Frank的猜想是不成立的.
设a1是任意有穷值设ω是如下Riccati方程式的非常数解
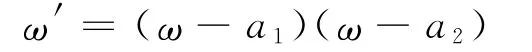
设
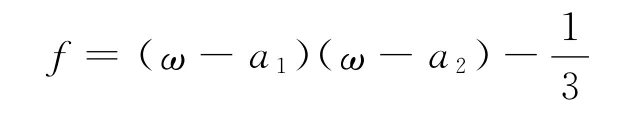
容易得到
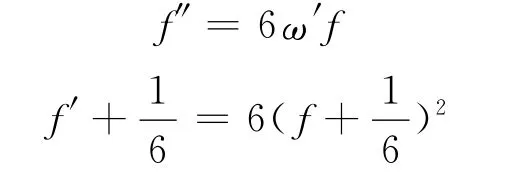
可以看到0是ω′的Picard例外值,并且f和f″CM分担0,并且f和f″IM分担,但是f不恒等于f″.所以考虑,如果在IM分担b这个条件下再附加某些条件,能否使f≡f(k)的结论成立.陈春芳[6]通过限制f的极点重数,讨论了f和f′IM分担公共值的唯一性问题,得到了下面的结论:
定理4 设f为非常数亚纯函数,且f的极点重数n≥11,a和b为两个相互判别的有穷复数,若f和f′IM分担a和b,则f≡f′.
针对以上结论,结合权分担的思想,对定理3中的条件进行了改进,得到如下结果:
定理5 设f(z)是一个非常数的亚纯函数,k为正整数,并且f(z)的极点重数大于等于2k+4.如果f(z)和f(k)(z)分担(a,∞),(b,1),这里a和b(≠0)是两个相互判别的有穷复数,那么f(z)≡f(k)(z).
2 相关引理
引理1 设f是非常数亚纯函数,f和f(k)分担(0,∞),(1,1),并且f的极点重数大于等于2k+4.如果f不恒等于f(k),则有
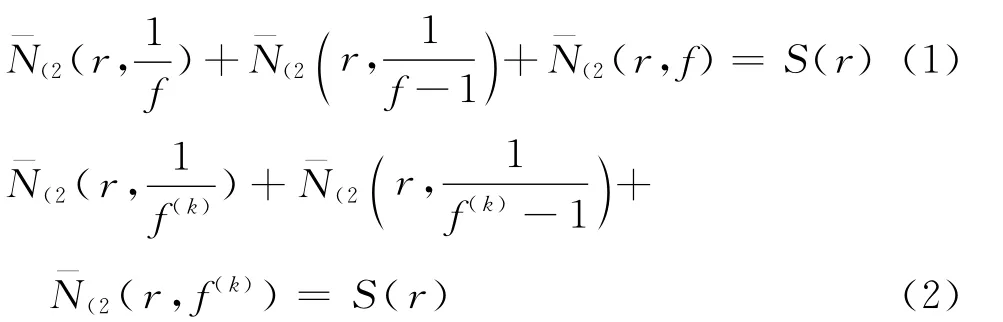
证明 设
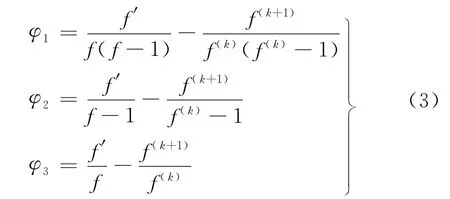
由条件知,φi(i=1,2,3)不恒等于0.因为f不恒等于f(k),所以
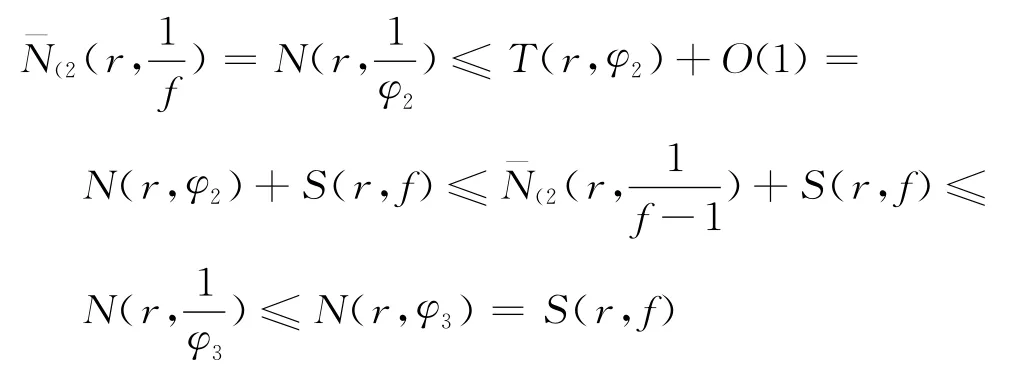
由于f和f(k)以CM分担0,所以
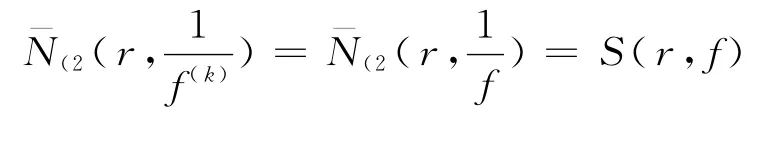
又由式(3),有
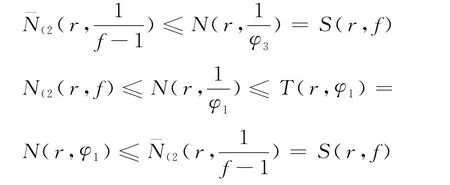
由f和f(k)分担(1,1)知
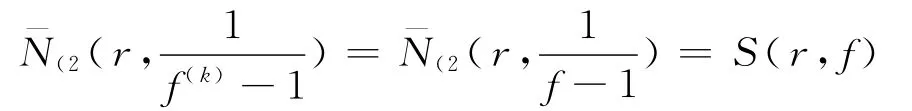
另外,由于f的极点重数大于等于2k+4,故
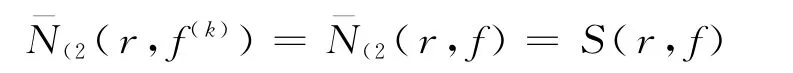
故引理得证.
引理2[7]设f1和f2是两个非常数亚纯函数,且满足其中i=1,2.如果那么存在2个满足|s|+|t|>0的整数s和t,使得
引理3 设f(z)是一个非常数的亚纯函数,k为正整数,并且f(z)的极点重数大于等于2k+4.如果f(z)和f(k)(z)分担(0,∞),(1,1),那么
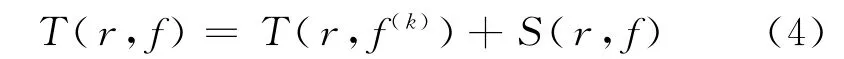
证明 如果f(z)恒等于f(k)(z),则引理3成立.
假设f(z)不恒等于f(k)(z).设
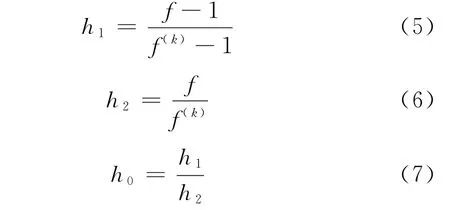
由式(5)、式(6)、式(7),可知
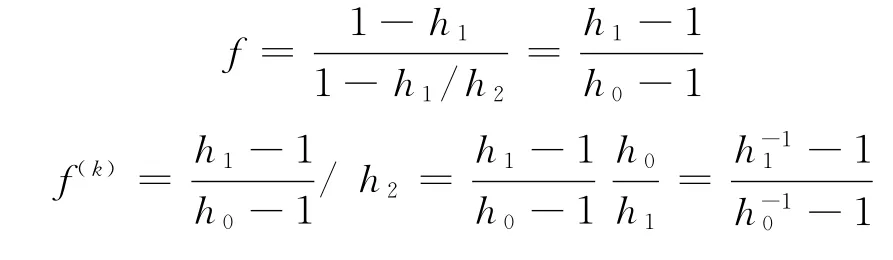
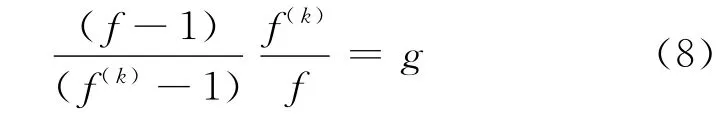
因此,T(r,g)=S(r),并且由式(8),可知
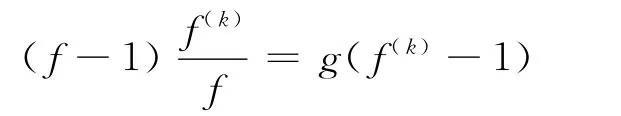
又f(z)和f(k)(z)分担(0,∞),则
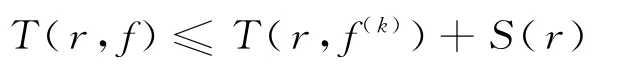
再由式(8),可知
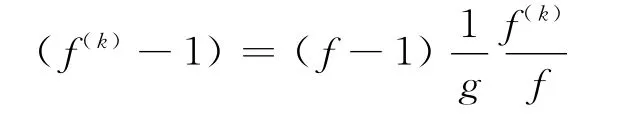
同理,有
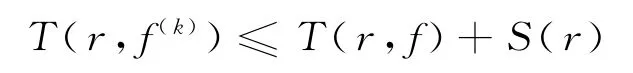
从而引理3得证.
3 定理5的证明
假设f不恒等于f(k),分两种情况进行讨论.
情形1 假设ab≠0,则有
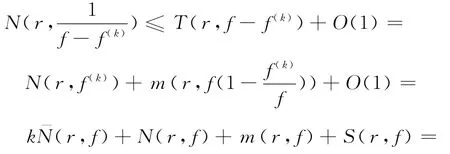
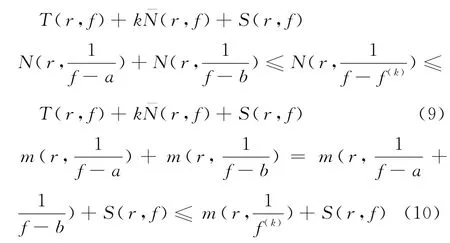
将式(9)和式(10)相加,可知
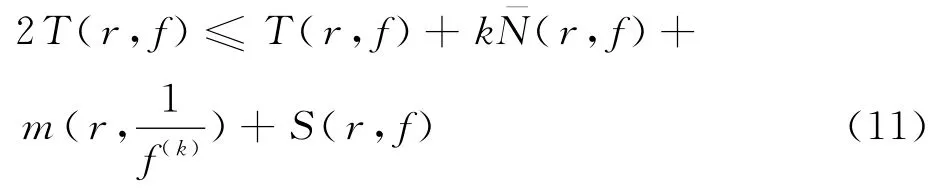
另外
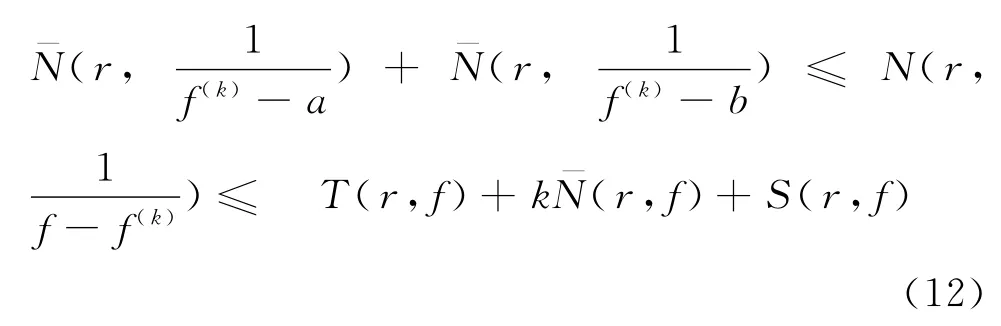
又因为
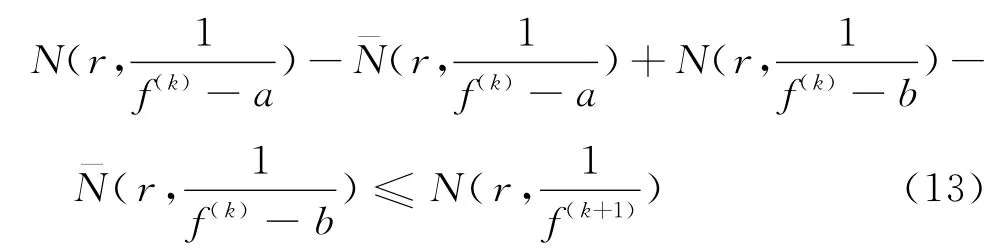
将式(12)和式(13)相加,可知
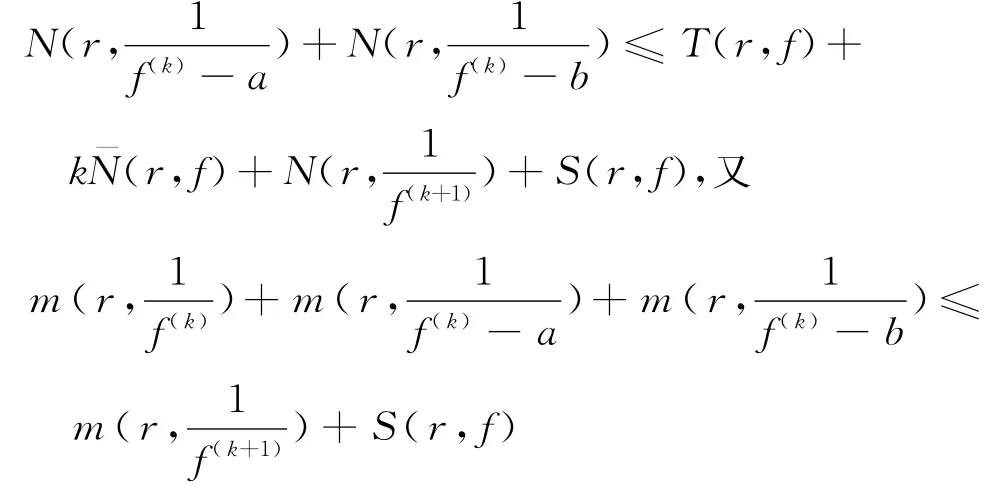
所以,可知
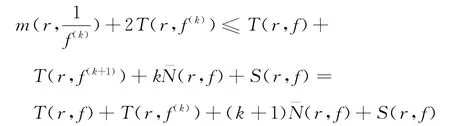
再由式(11),可知
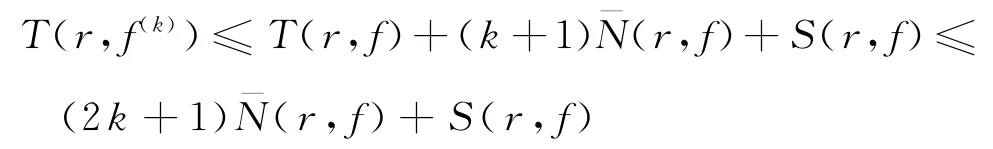
由于f的极点重数大于等于2k+4,所以
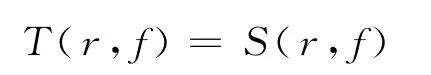
矛盾.
情形2 设ab=0,不失一般性,设a=0,b=1,则定理即为f(z)和f(k)(z)分担(0,∞),(1,1).因此,设
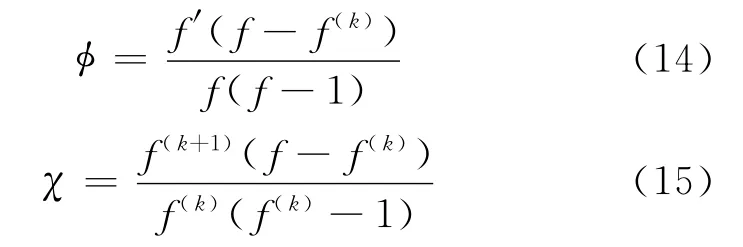
由式(12)计算,可知
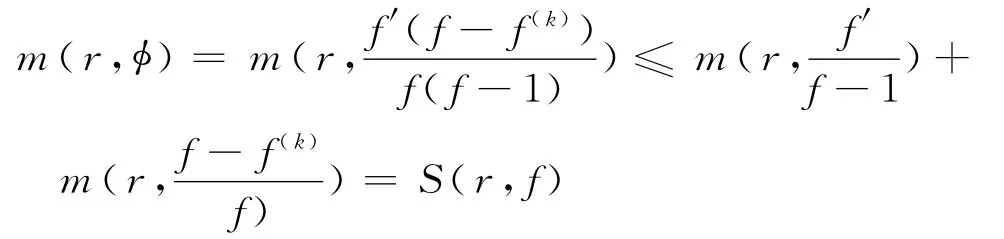
并且由φ的构造及f的极点重数大于等于2k+4,可以看到
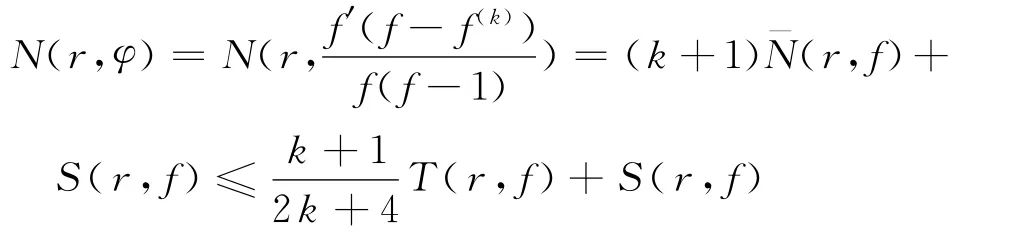
所以
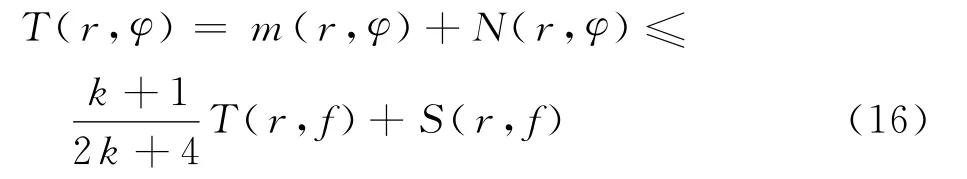
同理,由f和f(k)分担(0,∞),引理3和式(15),可知
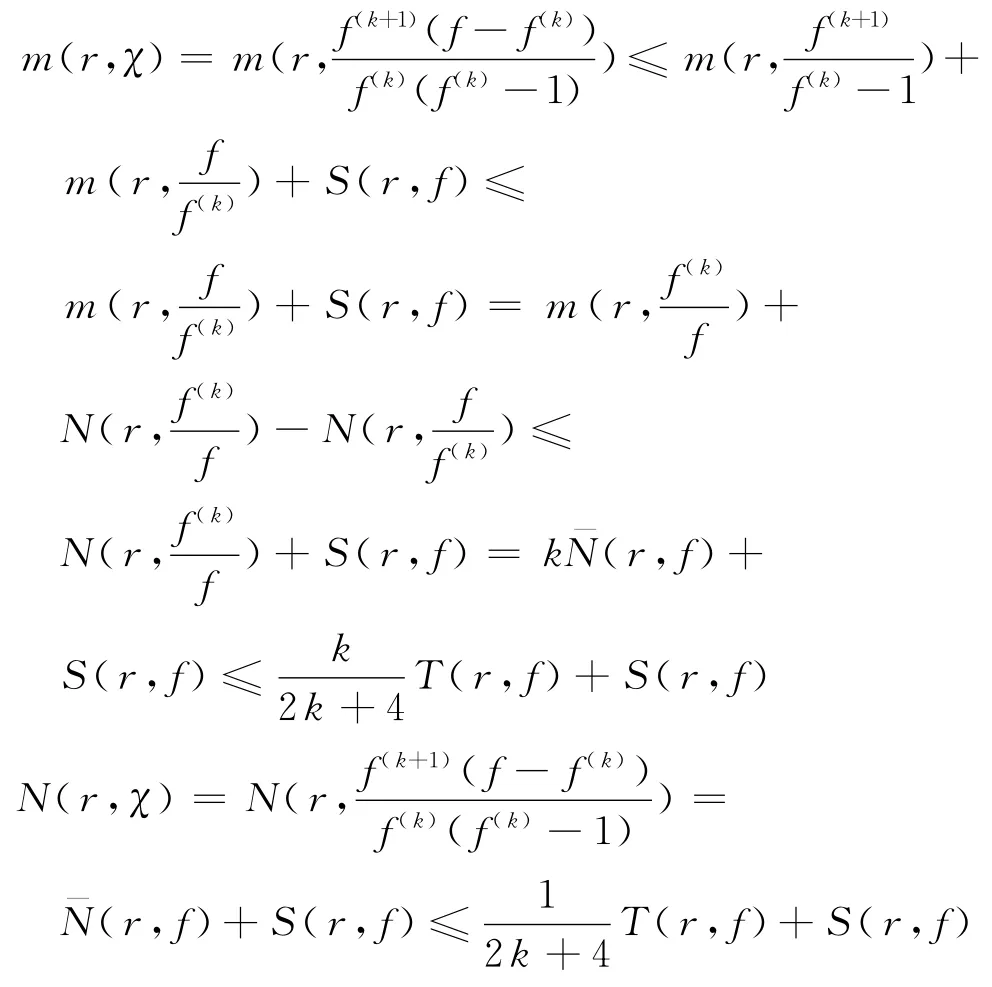
所以
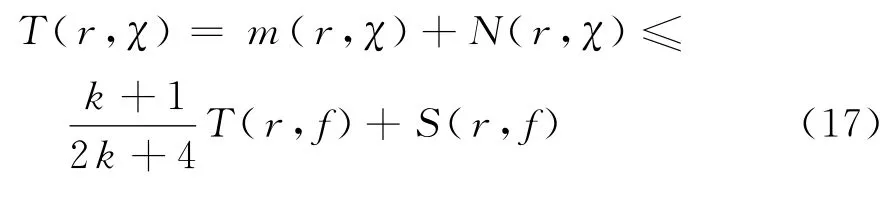
设H(m1,n1)=m1φ-n1χ,这里m1和n1都是正整数.分两种情况进行讨论.
情形1 假设存在两个正整数m0和n0,使得H(m0,n0)≡0.因此,得到
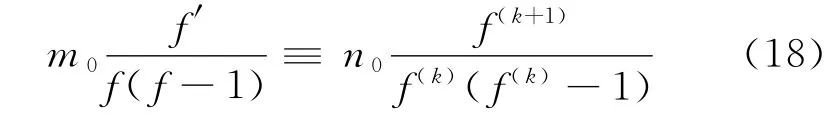
对式(18)积分,可知
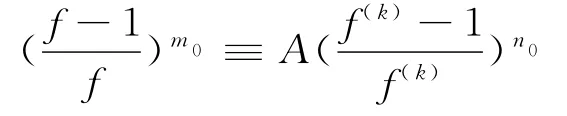
这里A(≠0)是一个常数.由引理3结论,所以m0=n0,从而f((1-A1)f(k)-A1)=f(k).
若f的极点是n重,则上面等式左边的极点数是n+n+k=2n+k,右面的极点是n+k,所以n=0,与f的极点重数大于等于2k+4矛盾.
情形2 假设对任意两个正整数m1和n1,使得H(m0,n0)不恒为0.设z0是f和f(k)的重数分别为n1和m1的公共零点,所以由H 的构造知H(m1,n1)(z0)=0.设z1是f-1和f(k)-1的重数分别为n1和m1的公共零点,同理知H(m1,n1)(z1)=0.因此,由式(16)和式(17),可知
由第二基本定理和式(19),可知
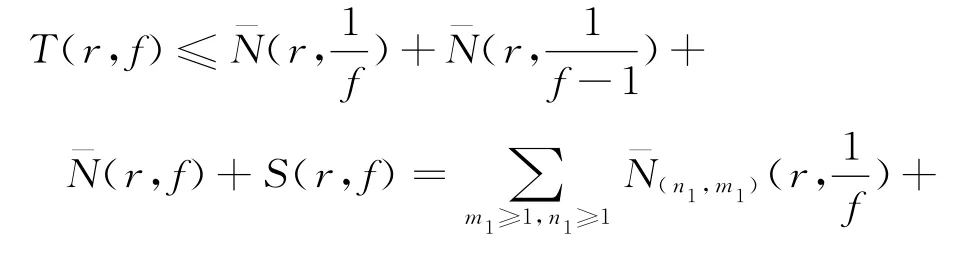
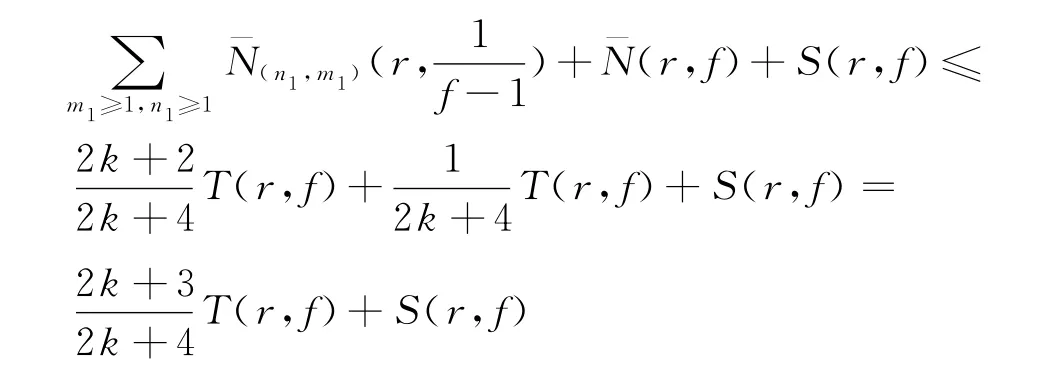
即T(r,f)≤S(r,f),矛盾.故定理5得证.
[1] 杨乐.值分布论及其新研究[M].北京:科学出版社,1982.
[2] Gundersen G G.Meromorphic functions that share two finite values with their derivatives[J].Pacific J Math,1983,105(2):299-309.
[3] Frank G,Ohlenroth W.Meromorphe funktionen,die mit einer ihrer ableitungen werte teilen[J].Complex Variables,1986,6(1):23-37.
[4] Frank G,Weissenborn G.Meromorphe funktionen,die mit einer ihrer ableitungen werte teilen[J].Complex Variables,1986,7(1/2/3):33-43.
[5] Yang Chong-jun,Yi Hong-xun.Uniqueness theory of meromorphic functions[M].Beijing:Science Press,2003:415.
[6] 陈春芳.亚纯函数及其导数的唯一性[J].南京师范大学学报,2004,27(3):36-39.
[7] Zhang Q C.Meromorphic functions sharing three values[J].India J Pure Appl Math,1999,30(7):667-682.

