基于DEA的中国区域R&D效率测度及聚类分析*

段宗志 曹 泽

基于DEA的中国区域R&D效率测度及聚类分析*

段宗志 曹 泽

（安徽建筑工业学院，合肥 230601）

通过测量我国31个省级区域R&D全要素效率、单个投入变量和单个产出变量的效率，并依据三种产出导向的效率得分对各决策单元（DMU）进行聚类分析。我们发现北京、上海在技术交易（技术开发、咨询与服务）CCR效率方面具有绝对优势；以中部各省为主体的九省市及北京、上海科技论文产出效率得分表现突出；浙江、广东、江苏、山东等六省市在技术创新与发明方面居于领先地位；而大部分西部地区以及福建、江西科技产出CCR效率全面落后。

R&D效率；数据包络分析；聚类分析

高效的R&D活动是国家、地区和企业竞争力的源泉。为了促进R&D效率提高，必须能正确地测量和评估R&D的效率，许多学者关注并研究R&D效率的测量问题。衡量绩效的方法如比例分析法、加权平均法、变异系数法等，都只能针对单项指标的绩效进行评比，而多指标的综合性评估，容易受决策者主观意见对权重的影响，或是利用数学期望值估计，使得绩效评估的结果较不客观。因此，本研究应用DEA绩效衡量工具进行运算分析，通过收集各地区决策单元（DMU）的投入产出数据，对决策总体进行效率评估，找出无效率决策单元，发现差距存在的具体影响指标及差距的大小。并以DEA得分为基础，对各决策单元分层聚类，帮助我们对不同类别的地区进行比较研究。

一、理论背景

（一）关于R&D效率

众所周知，效率被定义为产出与投入的比率。相同投入情况下产出越多，或是产出相同情况下投入越少，都被认为是生产效率的提高。在大部分情况下，我们可以容易地测量单个投入指标的效率，比如：劳动生产率、资本效率。他们都是单个产出与单个投入的比率。然而，单个要素的生产率并不能解释产出变化全部影响因素。为了克服单个要素生产力测量中对生产效率变化解释力的不足，人们引入了全要素生产率（TFP），以测量单个投入要素作用之外的效率变化。它等于产出的增长率减去单个投入要素的平均增长率［1］。

（二）关于DEA

DEA是一种不需要作任何先验性假定的非参数效率测量方法。一个决策单元的DEA效率可以通过估计其输出与输入的比率和与其他决策单元的比较予以评估。DEA模型可以划分为CCR型和BCC型。两种模型的区别在于它们分别处理的规模报酬假设不同。前者假定生产活动的规模报酬不变；而后者假定规模报酬可变［2］。因为R&D活动在大部分情况下显示出规模报酬不变的特点，因此本篇采用CCR型的DEA方法。DEA模型还可以根据模型要解决问题的目标予以划分：最大化产出或是最小化输入。因为R&D的目标在于扩大输出而不是减少投入，因此这里采用输出导向的DEA模型。

输出导向的CCR型线性规划式可作如下表示：假设一生产过程的投入与产出可能集为P，其中P中有n个同质 （homogeneous）的决策单元（DMU），每一个DMU使用m项投入x，并获得s项产出y。则其中第k个DMU的效率，表示为

这里xik，是第i个输入变量，yrk是第r个输出变量，vi是第i个输入变量的权重，ur是第r个输出变量的权重，k表示被测量的决策单元。为了测量每一个决策单元的效率，k个决策单元，模型将重复的分析k次。是一个大于0的常数，它的存在是为了保证各投入产出变量的权重非0。

二、数据的选择与处理

（一）变量的选择

关于R&D计算中的要素投入，无外乎资本投入和劳动投入。劳动投入即是R&D人员数，取不同年度的存量。R&D支出或研发强度为资本投入，在过去的文献中这一数据一般都取流量。本文认为科研活动所需要的实验设备和仪器等各种科研物质手段，是长期累积的结果，应当取存量。t时期的R&D资本存量（Rt）等于当期新增加的投入rt加（t-1）期的存量（Rt-1）再减去折旧（为折旧率 δ）。

为了计算初始的R&D资本存量，我们先假定过去每年投入的增长率为常数λ，则：

在用于表明R&D产出的变量选取方面，不同学者的选择互有差异，有的只把专利数量或是根据技术重要性或质量调整后的专利数量作为产出对象。有的认为专利只代表了R&D产出的一个部分。科技期刊发表的论文数、技术收支盈余数以及新产品开发的数量都是R&D的产出变量［3］。参考过去文献产出变量选取方案，结合资料的可获得性，本文拟选择技术交易成交额、论文产出和专利产出三个R&D产出变量。这样就有两个输入变量和三个输出变量（见表1）。

R&D支出和研发人员数分别代表资本投入和劳动投入。技术成果交易额、科技论文和专利授权量作为输出变量。技术成果交易额是科技产出的最直接表征，它包括了技术开发、技术转让、技术服务和技术咨询等几个方面，R&D活动成果的主要反映就是技术成果销售能力。科技论文是反映科技创新成果的重要形式，其中被SCI、EI和ISTP三大检索收录的论文在许多国家被用来作为衡量科技发展状况的依据，高校、科研院所广泛用它来评估教师和研究人员的科研能力［4］。专利在过去诸多研究中是最频繁使用，代表科技产出的变量。然而，由于许多专利申请不能得到批准，简单地使用申请的专利数量是有偏的，因此我们使用已经授权的专利以提高我们进行区域R&D效率比较的可信度。

由于R&D投入并不能立刻转化为输出，一般假定R&D投入与R&D输出之间有（3-5）年的滞后［5］。Graves（1996）认为一个谨慎的做法是用4年平均数［6］。因此本研究的投入变量选择从2006到2009年4年的平均数，而用2010年的数据作为R&D输出变量。

（二）数据的无量纲化处理

两个输入变量和三个输出变量主要来自于2007～2011的《中国统计年鉴》和《中国科技统计年鉴》。为了消除各种变量的量纲不同带来的影响，我们对原始数据进行标准化处理。处理方法是：把每一数值除以该数值所在变量的最大值，再乘以100。即，（其中i=1，2，3，4； j=1，2，…，31）。这样所有数据就转化成了百分制的标准化数据。

表1 R&D投入与输出变量

三、R&D效率的测量与聚类分析

本研究的分析过程划分为两个阶段。在第一阶段，根据标准化后的科技投入产出数据，使用Frontier4®测量R&D效率。在第二阶段，使用在第一阶段获得的R&D效率得分进行多元统计分析，先进行分层聚类分析，将各省、市、区按照R&D效率得分聚类，然后进行各类之间的横向比较，分析各类的特征，找出差距存在的原因，并予以评价。

（一）R&D效率的测量

首先，我们使用基本DEA模型，测量包括全部投入和全部产出的R&D效率。其次，由于DEA效率高度依赖于输入和输出变量的结合，除了基本的DEA模型之外，还可以做单个投入与全部输出，或是全部投入与单个输出之间的结构模型［7］。据此，我们就能够根据单个的投入或是单个的输出，来专门测量某一要素的效率指标。这样除基本模型外，另有五种模型分别是：资本效率模型、劳动效率模型、技术交易导向模型、论文为导向的模型和专利导向模型。依据这样的输入输出结构，可以得到基于六类DEA模型的全国31个省市区R&D效率得分（见表2）。

由表2可知，在31个省、自治区和直辖市中，在整体效率上，有7个地区为DEA有效，即在R&D投入产出中，其产出相对于投入，资源得到了充分利用。这7个地区分别为北京、上海、浙江、吉林、湖南、新疆和甘肃等。而其他各省区不同程度的存在着资源未能得到充分利用的情况，尤其是宁夏、江西、山西以及河北R&D投入产出效率不足50%。说明这些省区在资源配置、人才激励等科技政策执行上存在较大的问题，需要在科研体制改革和管理创新上多加努力。

表2 R&D效率得分

续表

不同模型中各个地区不同要素的效率值差异很大，比如吉林，它在论文导向的效率模型中，DEA得分为100%，而在以技术交易产出导向的效率模型中，DEA得分仅19.2%。显然，吉林在科学和期刊论文产出方面据有优势，而在技术开发、咨询与服务方面不足。

在投入效率方面，有6个地区资本投入达到有效 （效率值100%），只有两个地区人才投入CCR有效，同时我们看到，除广东、上海和浙江外，其他各地区资本投入效率均大于劳动投入效率。平均资本投入效率得分71.81%，平均劳动投入效率得分只有49.26%。说明我们的科技队伍地区之间严重不平衡，科技人才的整体素质亟待提高。因此，重视科技人才的选拔、培养和激励是提高科研整体效率的关键任务。

在三类产出导向的效率得分方面，代表技术开发、技术服务和技术咨询的技术交易效率存在严重的极化现象，北京、上海为CCR有效，而广西、贵州还不到3%。这一差距，除了显示我们的科技产出存在地区不平衡之外，也说明了地区之间的科技意识差异较大。要使R&D服务于经济发展，创造现实的生产力，必须加强技术利用，不仅要“学科学”，更要“用科学”。在科技论文产出效率方面上海、吉林和湖南效率100%，为最优。西藏、宁夏、内蒙和贵州等西部地区较差。一些高等教育发达，拥有名牌大学的地区在这种学术特点鲜明的科技产出中效率较高。专利产出中只有浙江效率为100%，排名二、三位的是广东和江苏，这三个省份是改革开放后中国经济较为活跃的地区，制造业的发展需要技术创新、产品创新，大批科技人才将研发面向生产实际，提高了技术专利成果的产出。

（二）R&D效率得分聚类分析

根据DEA基本模型和专门模型获得各省级区域效率之后，我们可以根据5种专门R&D效率得分进行R&D效率聚类，这样就能够很容易地知道每一类地区在科技发展方面的优势或不足。由于两种投入要素效率间的相关关系较高，并且投入要素与三种输出要素效率之间的相关关系也比较高，只有三种输出导向的要素效率值之间彼此不相关。因此根据全部五种专门的效率得分予以聚类就不合适。只能选择三种输出导向的要素效率值作为省级区域R&D聚类的指标。同时这样的选择，也从科研活动的结果方面对区域科技发展的强弱状况给予评价。

使用Ward’s方法和欧几里德距离进行分层聚类，全部31个省区可聚为4类，结果见表3：

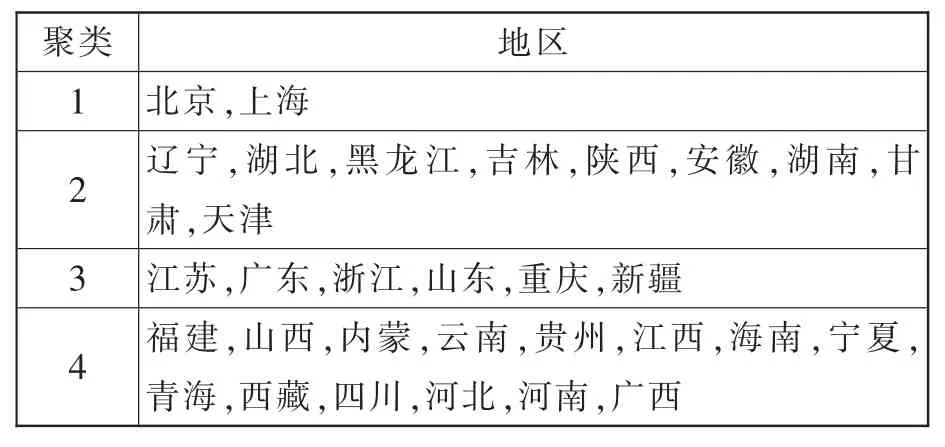
表3 R&D效率聚类

（三）方差分析

方差分析是一种假设检验，它是对样本观察值的差异进行分解，将某种因素下各组样本观察值之间可能存在的系统性误差和随机误差加以比较，据以判断各组之间是否存在显著性差异［8］。由前面的效率得分相关分析可知，据以聚类的三个因素对R&D效率得分彼此无关或最多表现为弱相关，因此我们在方差分析时无需考虑彼此之间的交互作用，只需做单因素方差分析。分别以技术交易、论文和专利为影响因子，根据表2中效率的得分，计算各离差平方和和F值，方差分析结果见表4。

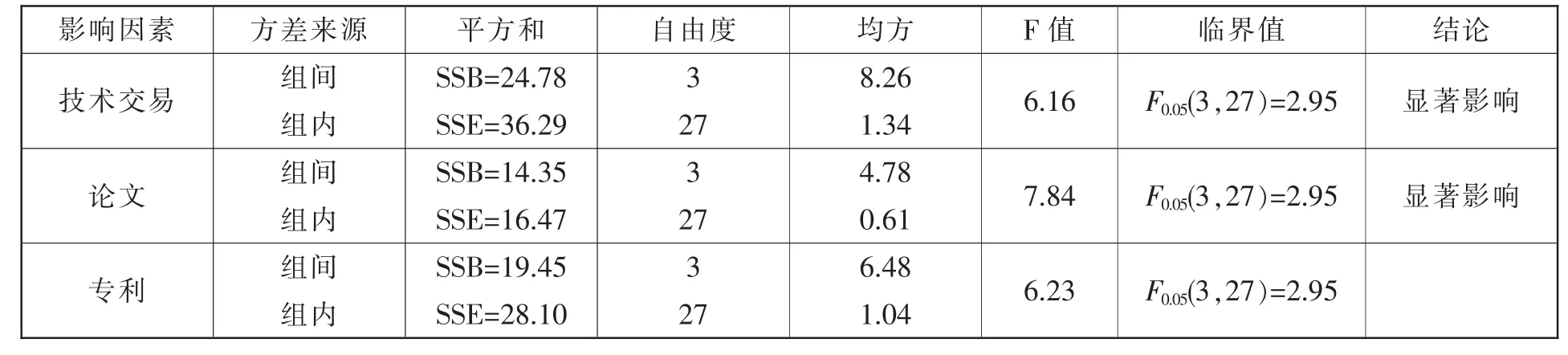
表4 方差分析比较结果

由表4，不同因素下的组间离差远大于组内离差，F值大于临界值。我们可以判别在显著性水平为0.05的水平上不同类别具有显著差异，于是我们认定，与某种影响因素对应的4个类别中均值较大的类别即为效率优秀者。进一步给出三种因素下4个类别的得分均值（见表5）：

表5 各类别不同因素输出导向得分均值及比较

从表5我们看到，由北京、上海构成的第一类在技术交易导向效率方面平均得分100，远远超出其他各类。因此我们说，北京、上海在技术开发、技术咨询和技术服务方面绝对领先。同时我们看到，这两个地区在论文方面也领先于其他各类。显然，作为全国科技、教育、经济和文化的中心，这两个地区聚集了大量的科技资源。

由辽宁、湖北、黑龙江、吉林、陕西、安徽、湖南、甘肃和天津九个地区构成的第二类，在科技论文方面平均得分达到88.2，尽管稍低于第一类的北京、上海，但相对于第三、第四类地区优势明显，其主要原因是上述地区都拥有全国排名靠前的重点高校，科技人才资源丰富，学术氛围浓厚。但是该地区经济较不发达，R&D费用投入不足，导致以技术开发、转让、咨询和服务为内容的技术交易，以及企业技术创新和专利发明等方面滞后。

江苏，广东，浙江，山东，重庆和新疆六个省区构成第三类地区。它们在专利效率得分方面优于其它各类，这其中既有技术发明、产品创新方面领先的东部发达地区，也有因为低投入引致高效益的西部省市。我们看到东部四个省份正是我国经济发达、制造业聚集的地方，他们充分挖掘科技服务于地方经济的作用，科技产出不只是停留在实验室内，而是面向生产实际。

第四类主要是西部各省区，但也包括了东部的福建省，和中部的江西、山西等中部省份。它们在三种导向的产出得分中排名均靠后。我们看到这些地区不仅科技投入不足，科技产出绝对落后，而且科研效率也相对低下。尤其不幸的是四个类别中这样的省区比例最高，接近二分之一，可见提高国家整体的科研水平、科技效率任重道远。

四、结 论

综合DEA效率得分与聚类分析，北京、上海拥有全国最优质的科技资源，包括人才和科研设备，因此他们在科技产出的两个方面具有较高的效率。但是在技术创新和专利产出方面效率不足。以中部各省为主体的第二类同样具有科教优势，但是由于中国改革开放进程中，中部地区屡屡成为政策洼地，因此，在科技产出的形式和成果的利用方面，还需要国家的政策扶持，以及经济与科技发展的良好互动。第三类地区以中国东部沿海四省为主体，众多民营企业、外资企业的竞争发展，催生了产品的不断创新，带来技术发明的高产出。上述三个类别的地区各有特点，同时也存在着不足，比如：第三类的东部地区应当在科技咨询，技术服务方面进行改善提高；而第二类地区应当注意把科技与产业密切结合以提高现实生产力；同样北京、上海要加强技术发明和新产品的开发创造；而各方面都比较落后的第四类地区更应当通过科技人才的培育和科技资源的优化配置等，提高产出效率，实现R&D水平的提高。

[1]Bartelsman E J,Gray,W.The NBER Manufacturing Productivity Database [R].Massachusetts：National Bureau of Economic Research,1996,(2):215-236.

[2]Charnes A,Cooper W W.The Non-Archimedean CCR ratio for Efficiency Analysis:A rejoinder to Boyd and Fare [J].European journal of Operational Research,1984,(5):333-334.

[3]Park K M,Shin J S,Park Y T.A Study on the Aggregation and Structuring of Technological Knowledge Indicators [J].Technology Innovation Research,2003,(11):125-145.

[4]OECD.OECD Science,Technology,and Industry Scoreboard[R].Paris:OECD,2001.

[5]Scherer F M.The Propensity to Patent[J].International Journal of Industrial Organization,1983,(1): 107-128.

[6]Graves S B,Langowitz N S.R&D Productivity:A Global Multi-industry Comparison [J].Technology Forecasting and Social Change,1996,(2):125-137.

[7]Jenkins L,Anderson M.A Multivariate Statistical Approach to Reducing the Number of Variables in Data Envelopment Analysis[J].European Journal of Operational Research,2003,(1):51-61.

[8]徐国祥，刘汉良，等．统计学［M］．上海：上海财经大学出版社，2010:178．

（责任编辑 明 笃）

F224

A

1001-862X（2012）04－0045－006

安徽省软科学研究计划项目（10030503055）；教育部人文社科规划项目（11YJA630003）

段宗志(1965-)，男，安徽太湖人，副教授，主要研究方向：建筑经济、西方经济学。