基于Monte Carlo法的光电跟踪测量系统精度分析和布站优化方法＊

张振铎，张 彬

（中国科学院 长春光学精密仪器与物理研究所，吉林 长春 130033）

引 言

靶场光测设备是对弹道导弹、飞行器、卫星等武器设备进行精确观测的有效工具，它通过角度测量和交误差分析实施对空间目标精确定位以完成外弹道的观测。测量中的各种误差源直接决定定位精度［1，2］。但误差并不是越小越好还要受到研制成本等多种因素的制约，同时各种误差因素对光测系统而言，其重要性和影响方式有所不同，对各种误差源进行精确分析对靶场光测设备有重要的实际意义。一方面在设计的初期研制过程中可以对设备测量不确定度有影响的各种因素进行严格的过程控制，同时对优化材料选用、设备制造等多种环节进行控制，以更低的研制成本更好地满足用户的使用要求［3－5］；另一方面通过对光测设备进行合理的布站以提高光测设备测量精度［6，7］。光测设备的精度模型和光测设备的布站是两个相互联系的问题，对光测设备的布站优化必须以精确的误差模型为基础，同时对光测设备的误差分析也需要给出在一定布站方式下对特定目标轨迹的精度分析。

文中以光电经纬仪为例，对光电经纬仪建立了精确的Verilog－A模型，并在此基础上使用 Monte Carlo法对光电经纬仪的各种误差源的影响进行了详细的统计学分析和研究，并针对弹道导弹不同的布站方式进行数值分布，给出能适应不同靶场地形的通用的布站优化方法。

1 光电经纬仪的误差模型

文中提出的误差分析方法具有一定的通用性，使用通用的模拟系统建模语言Verilog－A以对光电经纬仪建立数学模型，并在数学模型中对测量精度有影响的各种误差源进行建模。Verilog－A提供了层次化的模拟系统模型构架，可以一定的数学表达式在抽象的层次上对系统建模，以方便系统的分析设计和验证。Verilog－A支持直流、交流、瞬态、Monte Carlo法等多种分析方法。提供给用户一定的设计参数，用户使用Verilog－A模型可以对设备的性能进行仿真分析进一步指导光测设备的应用。对各种光测设备建立通用的Verilog－A模型具有非常重要的实际意义。光电经纬仪的Verilog－A模型分为基本模型和误差模型，如图1所示。

图1 评估光电经纬仪测量误差的VerilogA模型框图Fig.1 The verilog A model for theodolite measure error evaluation

其中基本模型实现光电经纬仪的基本功能，即实现空间目标3维坐标（x，y，z）到俯仰角E和方位角A的转换：

误差模型使用坐标变换的方法，光电跟踪经过了基座坐标系、水平轴坐标系、照准部坐标系、相面坐标系，分别引入竖轴误差、横轴误差、照准轴误差和传感器误差，同时编码器也会引入编码器误差，在坐标系X1（x，y，z）经过旋转变换转到坐标系X2（x′，y′，z′），旋转θ角的旋转变换矩阵为M（θ），则同一点在X1中坐标与X2中坐标的关系为：

由于旋转变换矩阵的逆矩阵为：

得到：

光电跟踪依次经过了基座坐标系、水平轴坐标系、照准部坐标系、相面坐标系等旋转变换。各误差源所引入的旋转变换矩阵定义为Mi（i＝1，2…n），则在相面坐标系中单位光轴方向矢量（1，0，0）T在基座坐标系中的坐标可以表达为：考虑到方位角和俯仰角旋转方向的定义，各坐标系间旋转矩阵如表1所示

其中rot x，rot z，rot y分别为绕x，z，y轴的旋转变换矩阵，在旋转角很小时可以表示为：

表1 光电经纬仪误差模型中旋转变换Tab.1 The rotation transformation used for theodolite intercross measure model

坐标变换法是一种对光测设备误差源进行表达的通用的方法，使用此方法可以方便地对光电经纬仪建立包含各种误差源的准确的数学模型，并进一步建立光电经纬仪双站交汇测量模型如图2所示，输出dx，dz，dy分别为x，z，y三个方向上的交汇测量误差。其中交汇测量模块在异侧布站时使用K公式，在同侧布站时使用L公式，在Verilog－A模型中需要对除法运算分母做限幅处理以避免在平衡点处出现收敛问题。

图2 光电经纬仪交汇测量模块Fig.2 Theodolite intercross measure model

2 基于Verilog－A模型的误差分析法

针对上述光电经纬仪的数学模型进行统计分析，基本模型参数如表2所示。使用两种基本的误差分析方法，即最坏情况法分析和Monte Carlo法分析。计算了各种单项误差对系统性能的影响。现使用的分析方法具有一定的通用性，可用于各种光测仪器的误差计算中。

2.1 最坏情况法分析法

在最坏情况下假定所有的误差源都取最大误差，由于在实际情况下所有的误差源不是同时取得最大误差数值，因此最坏情况分析将得到较为悲观的预测数值，但这种分析方法可以快速估计各单项误差对系统误差影响程度和影响方式，同时给出理论上最大误差。使用此模型仿真了各单项误差都取最大数值的最坏情况，误差主要影响方位角A，而对俯仰角E影响较小。其中编码器误差直接加入到方位角和俯仰角误差中，而传感器误差、照准差、横轴差对系统误差的影响相对较为复杂，可以通过扫描相关误差参数计算出各误差参数对系统性能的影响。

表2 光电经纬仪模型参数选取Tab.2 Parameter selection for intercross measure model

使用该模型仿真了因俯仰角变化而引起的传感器误差、轴系照准差和水平轴误差A分量的变化曲线，如图3所示。从图3中可以看出，随着俯仰角的增加，三种误差源快速增加，文献表明照准差和水平轴误差的δE分别与sec（E）和tan（E）成正比，而水平轴误差与tan（E）与仿真结果相一致。同时可以看出在俯仰角较大时照准差对系统影响约为横轴误差的2倍。其中图3（a）表示了不同误差像素数目对系统误差的影响，传感器误差将随着误差像素数目的提高而增加，误差像素主要来自量化误差、细分误差和拖尾误差。

图3 俯仰角变化对传感器误差、轴系照准差和横轴误差的影响Fig.3 The influence of collimate error，vertical axes error，horizontal axes error

图4表示了竖轴误差随方位角和俯仰角变化曲线，其中左图表示竖轴方位误差随方位角和俯仰角的变化，可以看出竖轴差与方位角呈现正弦变化规律，且在竖轴倾斜方向上取得最大值，而随俯仰角E以tan（E）的规律快速增加；右图竖轴俯仰误差与俯仰角E无关且随方位角呈现正弦规律变化。此仿真结果与文献［1］论述相一致。图5表示总误差源随着方位角和俯仰角变化曲线，其中总方位误差随方位角A以正弦形式变化，其原因主要来自竖轴误差的影响，总方位误差随俯仰角E快速增加，主要受到横轴差、照准差以及传感器误差的影响。

2.2 Monte Carlo法分析法

在实际情况下各个单项是以一定概率分布的形式出现的，误差合成不是简单的线性叠加关系，传统的方法是基于统计学的t分布和χ2分布不确定度分析法，这种方法在处理测量误差传递时是基于线性化近似模型，同时假设各种误差源间是相互独立的。由于光测设备本身是一个复杂的非线性系统，同时误差源间也不是完全独立的，因此决定了这种方法具有一定的局限性。Monte Carlo法是一种通用的误差分析工具，它将设备的各项误差源表达为一定概率分布函数的形式，以相同概率分布产生随机数进行仿真计算，从而得到各种误差对系统的影响。系统的输出呈现出一定统计分布，通过使用MatLab统计学工具箱拟合的方法，可以得到系统输出的准确的统计分布函数，并以一定的数字特征如期望和方差的形式来表达。Monte Carlo算法的准确度主要取决于采样点的数目，可以通过合理的选用采样点的数目以达到所需的计算精度。

图4 竖轴误差随方位角和俯仰角的变化曲线Fig.4 The relationship of vertical axes error with azimuth and pitch angle

图5 最坏情况下经纬仪总误差随方位角和俯仰角变化曲线Fig.5 The total error with azimuth and pitch angle in the worst case

图6 Monte Carlo误差分析的一般步骤Fig.6 The general step for Monte Carlo error analysis

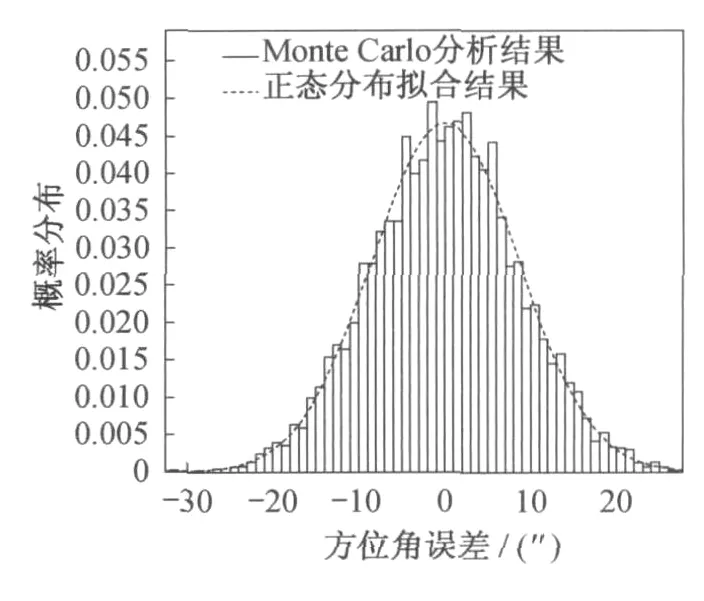
图7 Monte Carlo分析结果的正态分布拟合Fig.7 The normal distribution fitting result

图6表示了对系统进行Monte Carlo法分析的一般步骤。在Monte Carlo法分析中假设各误差源符合正态分布，精度范围为±δ，其中δ为正态分布标准差，各误差精度范围如表1所示。图7为方位角135°，俯仰角为45°时使用Monte Carlo法分析得到统计直方图以及使用MatLab统计工具箱拟合的结果，拟合得到正态分布δ＝8.53。使用此方法进一步分析了各种误差源对系统性能的影响如表3所示，是在考虑各种单项误差的情况下计算得到的系统的方位角误差和俯仰角误差。从分析结果看，照准差和传感器误差对总误差的影响最大。

3 基于Verilog－A模型的光电经纬仪布站优化

表3 A＝135°，E＝45°情况下 Monte Carlo法分析结果Tab.3 The Monte Carlo analytical result when A＝135°and E＝45°

基于Monte Carlo法的精度分析可以进一步应用于光电经纬仪的布站设计中，可以针对特定的地形特点和弹道轨迹使用Monte Carlo法仿真光电经纬仪的交汇测量过程，弹道轨迹公式如下：

现选择弹道发射后2s到7s进行理论弹道轨迹优化，弹道发射方向为X方向，弹道方程参数为v0＝4.5km／s，θ＝0.13，采用异侧布站方式，两站点坐标为（10km，20km，0）和（10km，－20km，0），使用K公式进行交汇测量，在只考虑经纬仪的测量误差的情况下，测量得到的x，z，y三个方向的误差曲线随时间变化曲线如图8所示。对其在仿真时间内的平均误差绘制统计直方图，并使用MatLab统计工具箱进行正态分布拟合得到如图9的计算结果，x，z，y三个方向的正态分布方差分别为1.168m、2.756m和0.515m。计算表明在垂直于飞行方向的z方向上误差最大，而在高度y方向下误差最小。

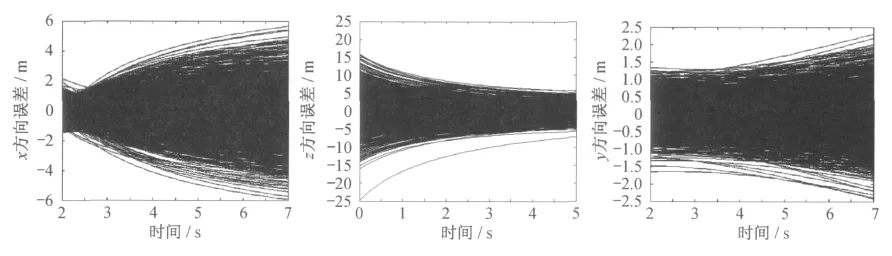
图8 仿真x，z，y方向测量误差随时间变化曲线Fig.8 The time variable measure error in the direction of x，z，y

图9 x，z，y方向平均误差直方图Fig.9 The average measure error histogram in the direction of x，z，y

在异侧布站情形下，设置站点z坐标分别为＋20km和－20km，使用Monte Carlo法仿真得到站点x坐标变化对交汇测量误差的影响，如图10所示，图中4条曲线分别对应于x，z方向站点定位误差d分别为0m，1m，2m和3m时系统三个方向上的测量误差，从计算结果可知站点定位误差在垂直于飞行方向（z方向）上影响较大，且在站点定位误差小于1m时，经纬仪本身误差起主要作用；而当站点定位误并差大于1m时，站点定位误差将成为主要的误差源。同时注意到当站点x坐标为20km时三个方向交汇测量误差均呈现最小值，为最优布站位置。仿真结果表明在飞行段x方向中部位置布站可以获得最小测量误差。

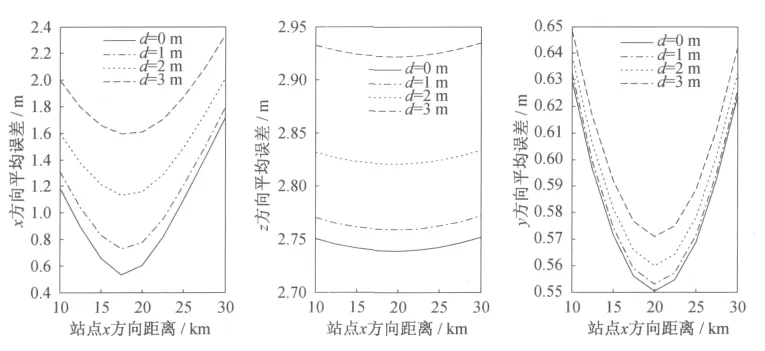
图10 异侧布站时不同站点位置精度下站点x方向距离与测量误差关系Fig.10 The relationship between measure error xdistance for different side station position optimization

设置站点x坐标位＋20km，－20km时，使用Monte Carlo法仿真了站点z坐标变化对交汇测量误差的影响，如图11所示，其中z坐标变化范围设置为1～20km，从仿真结果可以看出：

（1）x，z方向的误差随z方向站点距离减小而减小。

（2）而y方向误差随z方向站点距离呈现抛物线形态，且受布站位置误差的影响较大。在不存在站点定位误差时，站点z坐标为2.25km处，y方向误差最小；在布站定位误差为1m时，站点z坐标为5m处，y方向误差最小；站点定位误差为3m时，站点z坐标为5m处，y方向误差最小。定义y方向误差最小的点为最优布站点。

（3）最优布站点z方向距离定义为z＊，当站点z向距离z＜z＊时，y方向误差随z减少快速增加；当站点z向距离z＞z＊时，x方向和z方向误差随z增加快速增加。

图11 异侧布站时不同站点位置精度下站点z方向距离与测量误差关系Fig.11 The relationship between measure error z distance for different side station position optimization

文献［1］表明对定点测量时，当站点交汇角在90°左右交汇测量的精度最高，使用Monte Carlo法计算表明针对特定的弹道轨迹，在考虑经纬仪的各项误差源以及布站位置误差时，交汇测量精度将呈现更为复杂的关系，Monte Carlo法可以为光电经纬仪的布站优化提供指导。

使用Monte Carlo法进一步绘制了站点位置（x，z）变化时异侧对称布站情形下三维误差分布曲面如图12所示，使用此方法可以快速计算得到最优布站位置为（5km，20km，0）附近。如果给定一定的靶场地形信息，使用此方法可以针对特定靶场地形给出最优布站方式。

图12 站点位置精度1m时，x，z，y方向测量误差分布Fig.12 The x，z，y measure error distribution with 1mthe station position precision

4 结 论

对光电经纬仪建立了包含各种误差源的准确的数学模型，使用此模型进行最坏情况分析和Monte Carlo法分析，分析了各种误差源影响系统性能的程度和方式。进一步使用此模型对双站异侧布站情形进行了优化，分析表明针对沿x方向发射的弹道轨迹，飞行段x方向中部位置布站可以获得最小测量误差；布站z方向存在最优位置z＊，此处y方向交汇测量误差最小，当布站z向距离z＜z＊时，y方向误差随z减少快速增加；当布站z向距离z＞z＊时，x方向和z方向误差随z增加快速增加。提出的基于Monte Carlo法的布站优化可以进一步推广到特定靶场地形的情况，对经纬仪总体设计及布站方式的选择具有一定的理论指导意义。

［1］赵学颜，李迎春.靶场光学测量［D］.北京：装备指挥技术学院，2001：35－38.

［2］王家骐.光学仪器总体设计［D］.长春：长春光机所研究生部，2003：27－32.

［3］杜俊峰.光电经纬仪测量精度指标的确定［J］.应用光学，2006，5（6）：506－509.

［4］张 宁，沈湘衡.应用跟踪误差等效模型评价光电经纬仪跟踪性能［J］.光学精密工程，2003，18（3）：677－684.

［5］李 慧，沈湘衡.光电经纬仪数字化模型的建立方法及其应用［J］.光电子技术，2007，27（2）：97－100.

［6］侯宏录，周德云.光电经纬仪异面交会测量及组网布站优化设计［J］.光子学报，2008，37（5）：1023－1028.

［7］郭丽华，朱元昌.基于遗传算法的光电经纬仪布站优化设计［J］.仪器仪表学报，2010，5（4）：741－746.