二维数字图像相关方法的拉伸实验误差分析*
王 楠,李恩普,汤忠斌,李发东
(1.西北工业大学 理学院 陕西省光信息技术重点实验室,陕西 西安 710129;2.西北工业大学 航空学院,陕西 西安 710072)
引 言
数字图像相关(digital image correlation,DIC)方法是一种非接触、全场变形测量技术,因其具有设备简单、对环境要求低、测量精度高等优点,已被广泛用于材料的力学性能测试中[1,2]。DIC方法分二维(2-D)和三维(3-D)两种:3-D DIC需要两台摄像机,实验较为繁琐;2-D DIC仅用一台摄像机,且不需要相机标定。尽管2-D DIC精度略低于3-D DIC[3],但是通过修正系统误差,仍可达到相当高的精度,因此仍然具有相当高的实用价值。
研究人员对2-D DIC的误差做了大量的研究,且将误差源分为硬件和软件两类[4]:(1)硬件方面主要包括散斑图质量[5]、镜头畸变[6]、离面位移[3]等;(2)软件方面主要包括子区域大小[7]、相关函数[8]、亚像素插值[9]等。这些工作从原理上发展和完善了DIC方法,使其在实际应用上又向前迈进了一步。
力学实验中最常见是拉伸实验,将2-D DIC方法应用于拉伸实验已有很多报道[1,2],但却没有规范的实验方法,研究人员多是凭自身理解和经验进行实验。DIC作为一种图像测量方法,由硬件及实验方法引入的系统误差和偶然误差对测量精度和可靠性都有很大的影响,因此为提高实验的可靠性,对实验误差分析具有重要意义。
文中主要分析了实验条件对2-D DIC影响,对多晶铜试样进行拉伸实验,以应变片的测量结果为基准,将2-D DIC的测量结果与之比较,验证2-D DIC的测量精度,针对出现的误差,寻找误差源,并进行系统修正。
1 数字图像相关原理
DIC方法是通过处理变形前后被测物体表面的图像获得位移和应变场信息的测量方法。将变形前后的图像分别称为“参考图像”和“变形后图像”,利用灰度分布的相关性求形变量。首先在参考图像中定义计算区域(region of interst,ROI),一般为矩形。计算区域进一步被均分为虚拟网格,通过计算每个网格节点的位移得到全场位移信息。2-D DIC方法的基本原理在于对变形前后两幅图像中的相同像素点进行追踪或匹配,如图1所示,为计算P点的位移,在参考图像的计算区域内选择一个以P(x0,y0)为中心的含(2 M+1)×(2 M+1)个像素的正方形参考子区,在变形后图像中通过一定的搜索方法,按预先定义的互相关函数进行相关计算,寻找与参考图像子区的互相关系数最大或最小(取决于所选择的相关函数)的以P′(x′0,y′0)为中心的目标图像子区,从而确定P(x0,y0)点在X、Y 方向的位移分量U、V。
为了衡量参考子区与目标子区的相似程度,必须预先定义互相关函数作为评价标准,根据文献[4]的研究,选择归一化的最小平方距离函数(zero-normalized sum of squared differences,ZNSSD):

式(1)中,f(xi,yi)为参考图像中坐标(xi,yi)点的灰度,g(x′i,y′i)为变形后图像中坐标(x′i,y′i)点的灰度,fm、gm分别为变形前后图像子区的平均灰度。与其它相关函数相比,该函数具有抗干扰性强,对目标图像子区灰度的线性变换不敏感,相关系数峰值全场唯一且尖锐等特点,因而能更准确地寻找到整个搜索区域的相关系数极值。
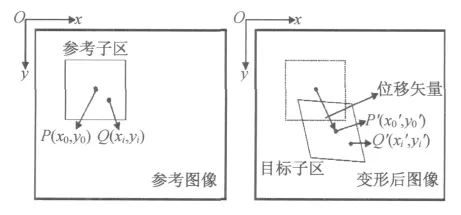
图1 正方形参考子区变形前和变形后的示意图Fig.1 Schematic of a reference square subset before and after deformation

图2 实验装置示意图Fig.2 Schematic of the experimental set-up
2 实 验
2.1 实验设备
实验装置简图如图2所示,采用Instron 5848试验机进行单轴拉伸加载。试验机载荷传感器分辨力为0.00001N,最大载荷2kN,位移传感器分辨力0.00001mm。图像传感器为一台大恒DHHV1303UM CMOS摄像机,分辨力为1280×1024pixel,镜头为Computar MLM-3XMP变焦镜头。实验过程中利用磁性底座把摄像机固定在钢铁基座上,以保证摄像机稳定且光轴与试样表面垂直,拍摄时用冷光源照明试样。
试样材料是牌号为T2的紫铜,几何尺寸如图3所示。由于相关运算的精度与散斑质量关系密切,因此为了增加散斑图的平均灰度梯度[5],实验中的散斑图是在白漆基底上喷涂直径约为0.5μm的雾化黑色碳素墨水颗粒得到的,如图4所示,白框为所选计算区域。

图3 试样的几何尺寸(厚度:0.5mm)Fig.3 Geometrical dimensions of the specimens(thickness:0.5mm)

图4 散斑图样Fig.4 Speckle pattern
2.2 实验过程
现从软件和硬件两方面分析了实验条件及设备可能引入的误差,确定最佳拍摄条件,并进行了拉伸实验。
2.2.1 软件计算误差
DIC方法是先计算位移场,然后再通过位移场计算应变场,先利用双线性插值法对散斑图像进行灰度的插值,然后利用式(1)计算插值后散斑图相关区域的相关系数,从而得到亚像素位移,再通过逐点局部最小二乘法[4]来计算位移的导数,即应变。
由于位移的误差会导致应变计算不准,因此为确定软件对实验图像的位移计算精度,选取一幅实验图像为参考图像,对其施加0.01~1pixel的模拟位移,比较计算得到位移和虚拟位移之间的差别。
2.2.2 硬件误差实验
在保证散斑图质量、光照的均匀、稳定及实验台隔振的情况下,2-D DIC的硬件误差主要由以下几方面引入,因此需逐个分析:
(1)拍摄条件的影响
影响图像拍摄的主要因素有:光圈、焦距、物距、像距、快门速度(也叫曝光时间)等。而图像的质量直接影响DIC计算的结果,现通过刚体平移和零位移实验来检验拍摄状况。
刚体平移由于不包含任何变形,所以DIC计算区域内的位移值应该是相同的,位移场应为一平面;零位移实验是对静止的试样表面连续拍照,然后对图像进行DIC计算,所得位移场应是全为零的平面分布。考虑到软件存在计算精度,因此若计算得到结果在软件计算精度范围内波动,则说明摄像机的拍摄状况比较理想。
(a)放大倍数影响
将镜头放大倍率调至0.3×和1.0×,各做一组零位移和刚体平移实验。刚体平移是样品在试验机上沿竖直方向平移,以0.03mm为步长,平移0.3mm,依次采集10幅散斑图像。
(b)快门速度的影响
快门速度需配合光源设置,设置不当也会影响成像,实验所用的摄像机快门速度可在1μs~1s范围内调节,但为了配合白光冷光源,快门速度必须设为10ms的整数倍。实验中,把镜头放大倍率设置在1.0×,在不同快门速度下拍摄零位移图像。
(2)离面位移实验
要成功地应用2-D DIC实验,要求试样表面应足够平,且与摄像机光轴尽可能垂直。然而实际应用中,因为加载装置的缺陷,以及材料的泊松效应[3,4],故试样表面会偏离理想平面,离面位移很难避免。为降低离面位移的影响,主要有两个办法:一是采用远心镜头,二是尽可能地将摄像机放置在远离试样表面的地方,近似形成一个远心成像系统[3,4]。由于实验中使用的镜头属于微距镜头,物距较短,不得不考虑离面位移的影响,因此通过数值计算,讨论了实验中可能出现的离面位移与测量应变的关系。
2.2.3 拉伸实验
为了验证DIC系统应变测量的精度,将多晶铜大试样单轴拉伸变形的DIC与应变片测量的结果进行比较。实验中,试验机每拉伸100~200μm记录一次载荷和应变仪读数,同时采集图像,直至试样拉断实验停止,每次实验记录40~50幅图像。
总共进行了7组实验,编号为A1~A7,为了对比和验证误差源分析的正确性,各组实验的拍摄条件不尽相同,其中,A5~A7实验条件相同,相应的摄像机参数如表1所示:

表1 A1~A7实验中摄像机参数Tab.1 Camera parameters of A1~A7
3 实验结果与讨论
3.1 软件计算误差
施加0.01~1pixel虚拟位移后的散斑图DIC计算结果如表2所示。可以看到,划线处的两个相对误差值差别较大,因而断定实验所用散斑图的DIC软件计算精度大约在0.04~0.05pixel之间,完全可以满足DIC实验要求。

表2 不同虚拟位移与DIC计算结果的比较Tab.2 Comparison of DIC results with virtual displacement
3.2 硬件误差
通过软件计算可知,DIC软件的位移识别精度满足实验要求,那么误差主要是由外部实验条件所引入的。
(1)拍摄条件的影响
(a)放大倍数影响
镜头0.3×放大倍率时的零位移实验X、Y方向的位移场U和V分别如图5(a)和5(b)所示,可以看到两个位移场均非理想中零附近的平面,而是呈波浪形分布,在1.0×放大倍率时所得结果与之类似。
由于刚体平移不包含任何变形,因此计算区域内的位移值应该是相同的。然而如图6所示,在镜头0.3×放大倍率时,平移量为0.15mm时的位移场V形状为一斜面,且其余平移位置的计算结果与之类似。以Vmax-Vmin来衡量整个计算区域位移偏差的程度,从图7中可以看到,在位移量比较大的情况下,偏差有增大的趋势,而且相比于0.3×放大倍率,1.0×放大倍率时增大得更快,说明镜头放大倍率越大,对测量结果的影响越大。

图5 0.3×放大倍率,零位移实验Fig.5 0.3× magnification,null displacement experiment

图6 0.3×放大率,刚体平移y=0.15mm时的位移场VFig.6 Displacement field along the loading direction(0.3×magnification,y=0.15mm)
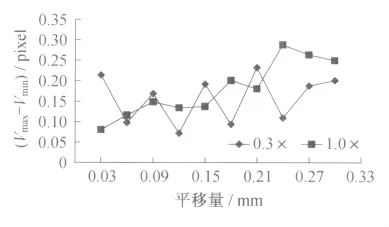
图7 刚体平移实验位移场Vmax-Vmin比较Fig.7 Comparison of Vmax-Vminin rigid body motion displacement field
零位移和刚体平移计算结果均说明摄像机拍摄状况不理想,导致采集到的图像不能准确反映试样表面变化,从而引入了大的实验误差。
(b)快门速度的影响
先前实验的快门速度均为默认的60ms。通过实验比较,发现当快门设为400~600ms时,计算出的位移场数值最为均匀。如图8所示,快门速度600ms时的零位移实验的位移场U和V整体呈水平面分布,这一分布特征与理论相符。图9对比了不同快门速度下零位移实验的Vmax-Vmin值,可以看到快门速度设为400~600ms以后,位移场偏差已经完全都在0.1pixel以内,因此可以断定,在此条件下,实验误差最小。
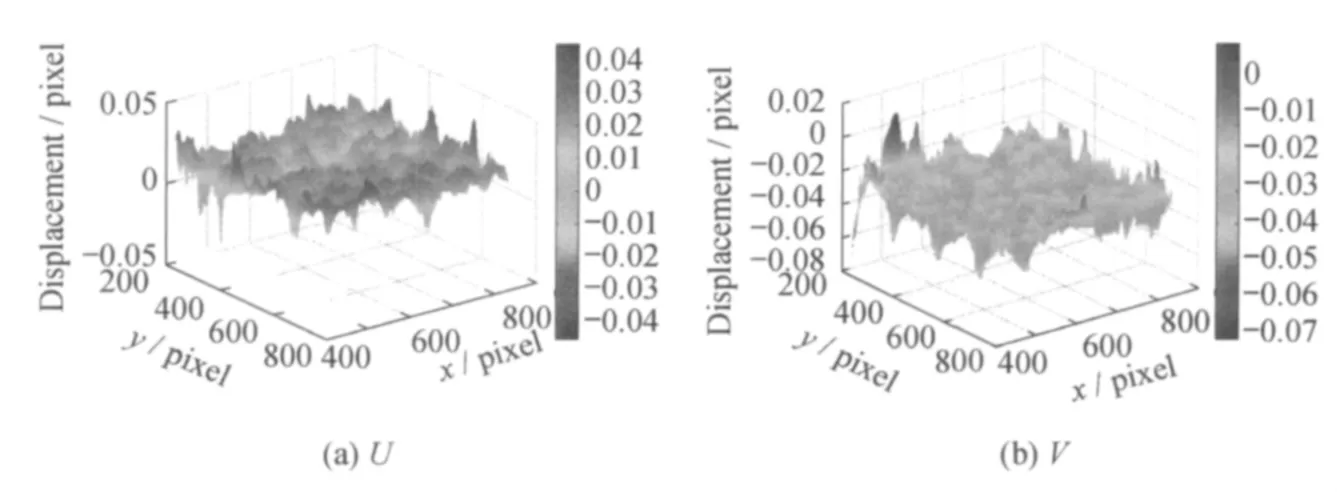
图8 快门为600ms时的零位移实验位移场Fig.8 Displacement field of null displacement experiment(shutter speed:600ms)
(2)离面位移
2D-DIC实验通常是凭经验判断试样表面与摄像机光轴是否垂直,因此偏差总是存在的。实验中使用的微距镜头因物距很短,对离面位移非常敏感,故必须具体分析其对测量结果的影响。
实验中的离面运动通常是离面平移和离面转动的叠加。假定试样表面与竖直方向夹角为θ,拉伸位移沿着试样表面向上,且在拉伸过程中角θ不变,仿照文献[3]建立离面位移模型,如图10所示。

图9 不同快门速度条件下,零位移实验Vmax-VminFig.9 Value of Vmax-Vminin null displacement experiment under different shutter speed
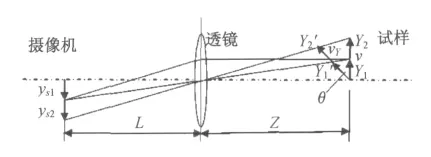
图10 试样表面和摄像机光轴不垂直对位移和应变测量的影响Fig.10 Effect of misalignment of the optical camera axis relative to the object plane
若试样表面和摄像机光轴之间是垂直的,试样表面沿着Y方向运动,有:
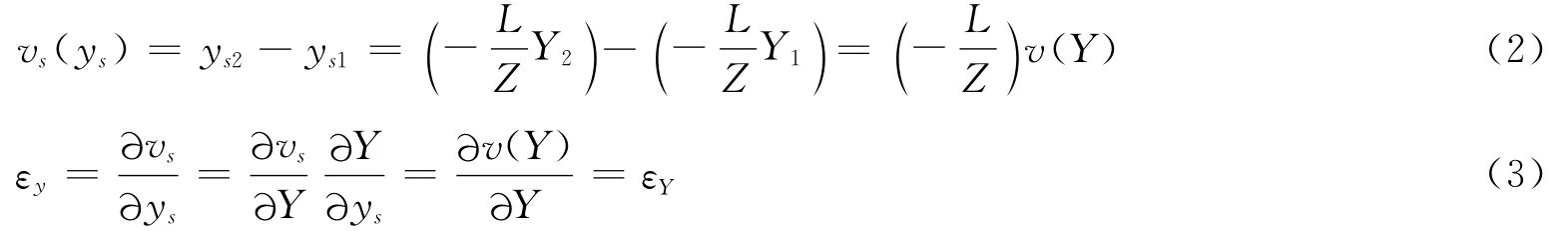
当试样表面向摄像机方向倾斜θ角时,试样表面沿着Y′方向运动,根据三角形几何关系,Y方向位移为:

取泰勒展式的一阶分量,得到:
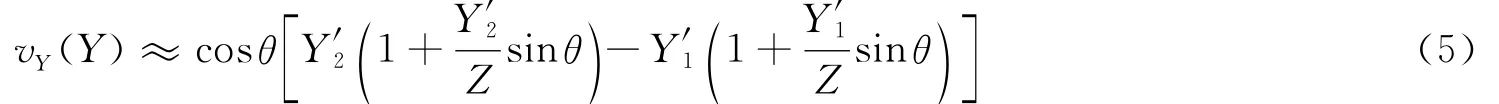
令Y′方向位移为vY′(Y′)=Y′2-Y′1,Y′1=Y′代表试样上任意的位置,则有:

综上可得:

此式即在试样表面任意一个位置Y′,DIC计算得到的应变εy与试样表面的实际应变εY′之间的关系,可以看到,应变与像距L无关。当Y′=0时,可简化为:
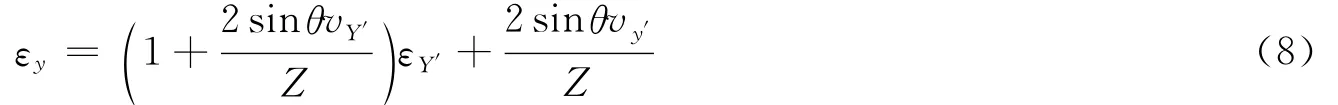
对于实验所用拍摄系统,利用式(8),可算得试样表面与摄像机的夹角θ,如图11所示,它由两部分组成,首先试验机上下夹具不对中,存在一定的倾角θ1;其次由于镜头自重使摄像机下倾,及摄像机基座不水平产生的倾角θ2。若要克服这个夹角θ,可以把摄像机安装在一个五维调整基座上进行调整,直到成像平面与试样表面平行。
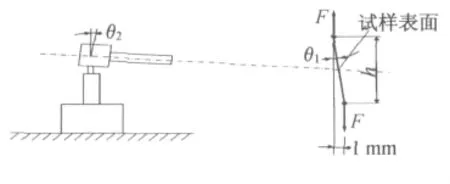
图11 实验系统的离面位移Fig.11 Out-of-plane displacement
3.3 拉伸实验
图12所示为应变片测量和DIC分析所得A2试样的应力应变曲线比较。可以看到应变片和DIC分析所得结果之间存在明显差别,而且其余六组实验结果相同。
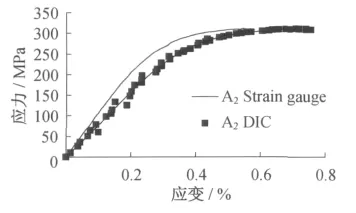
图12 A2试样的应力应变曲线Fig.12 Stress-strain curve of A2
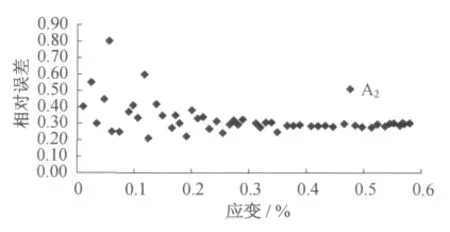
图13 A2试样DIC应变的相对误差随应变的变化趋势Fig.13 Variation tendencies of strain relative error of A2obtained by DIC method
为了比较DIC与应变片测量应变的差别,现以相对误差εi来衡量应变误差

式(9)中,i代表应变测量数据点序号。以横坐标为应变片测量的应变,纵坐标为DIC应变计算的相对误差,计算发现五组实验DIC应变测量的相对误差变化趋势相同,当εy<0.02%时呈散乱分布,而当εy>0.2%以后分布逐渐趋于稳定,图13所示为A2的计算结果。
分析εy<0.2%时相对误差的散乱分布,主要是因为实验开始阶段试样表面粗糙不平造成的,随着实验进行,试样逐渐被拉紧,其表面开始变得平整,这样的变化在一定程度上改变了试样与摄像机之间的距离[10],从而引入离面位移,导致测量的不准确。当εy>0.2%时,试样仅存在面内位移,因而七组实验的相对误差都逐渐趋于稳定。
为了横向比较每组实验间的相对误差的大小,取平均相对误差

式(10)中,N为每组实验测量应变数据点的数目,以ε平均为基准比较实验结果,如表3所示:

表3 A1~A7DIC应变相对误差比较Tab.3 Strain average relative error of A1~A7under DIC method
对比发现,相对于其它组实验,当快门速度设为600ms后,A3和A4的误差大幅减小,这与前面分析吻合,然而和应变片测量结果相比,DIC测量误差仍然较大,可以断定,这些误差主要是由摄像机的噪声和实验中的离面位移引起的。离面位移的影响前文已做理论推导,但要具体计算,则需要精确的角度测量才能完成,由于受实验条件限制,要到以后才完成。
3.4 误差修正
通过前面的论述,可以看到每组实验中DIC方法和应变片测量得到的应变的相对误差大致是稳定的,只是不同组实验的相对误差不同而已。如果实验的条件不变的话,其测量的误差也是恒定的,因此就可以对误差进行修正。
结合式(6)、式(7),令ε平均=εi,则有

取k=1/(1+ε平均)作为误差修正系数,其值与拍摄条件有关,因此,对应每种拍摄条件,需要事先标定一个修正系数k,才能对此条件下实验结果进行准确修正。计算得A1~A7试样的误差修正系数如表4所示。

表4 A1~A7各组实验的误差修正系数Tab.4 Error correction coefficient of A1~A7
可以看到,A5~A7三组实验因实验条件相同,系数几乎相同,从而可以认定在固定了拍摄条件后就有固定修正系数。其他几组系数的稀疏变化则是由于拍摄条件变化引起的。
根据式(11),现对A5~A7进行误差修正,表4中三个k值均可作为该条件下修正系数,取三者平均值对结果进行修正,如图14,可以看到经过修正的DIC曲线和应变片测量结果非常吻合,可见通过此法可以得到满意实验结果。

图14 A5~A7试样经过DIC应变修正后的应力应变曲线Fig.14 Modified stress-strain curve of A5~A7
4 结 论
DIC方法是一种很具吸引力的位移和应变场测量技术,可应用于不同领域中。然而,由于实验方法的不当,通常会引入一些误差。文中对2-D DIC的实验方法进行了研究,分析了多种拍摄条件下产生的实验现象及误差,并提出了相应的消除和抑制误差的措施,同时对DIC方法中因离面位移引起的误差进行了理论分析,得出了实际应变计算公式。最后利用2-D DIC方法测量了多晶铜试样的单轴拉伸应变,将结果与应变片测量结果进行比较,检验文中所用测量系统的精度,针对出现的误差,认为其主要来源于摄像机噪声及测试系统的离面位移,鉴于这两种误差源比较难以消除,探索了一种利用修正系数k对误差修正的方法,通过该方法对系统误差进行修正并得到满意的测量结果。
[1]TUNG S,SHIH M,KUO J.Application of digital image correlation for anisotropic plastic deformation during tension testing[J].Optics and Lasers in Engineering,2010,48(5):636-641.
[2]GRYTTEN F,DAIYAN H,POLANCO-LORIA M,et al.Use of digital image correlation to measure large-strain tensile properties of ductile thermoplastics[J].Polymer Testing,2009,28(6):653-660.
[3]SUTTON M A,YAN J H,TIWARI V,et al.The effect of out-of-plane motion on 2Dand 3Ddigital image correlation measurements[J].Optics and Lasers in Engineering,2008,46(10):746-757.
[4]PAN B,QIAN K M,XIE H M,et al.Two-dimensional digital image correlation for in-plane displacement and strain measurement:A review[J].Measurement Science and Technology,2009,20(6):62001-62005.
[5]PAN B,LU Z,XIE H M.Mean intensity gradient:an effective global parameter for quality assessment of the speckle patterns used in digital image correlation[J].Optics and Lasers in Engineering,2010,48(4):469-477.
[6]潘 兵,谢惠民,陈鹏万,等.数字图像相关测量中镜头成像畸变的估计和校正[J].计量学报,2009,30(1):62-67.
[7]PAN B,XIE H,WANG Z,et al.Study on subset size selection in digital image correlation for speckle patterns[J].Optics Express,2008,16(10):7037-7048.
[8]TONG W.An evaluation of digital image correlation criteria for strain mapping applications[J].Strain,2005,41(4):167-175.
[9]SCHREIER H W,BRAASCH J R,SUTTON M A.Systematic errors in digital image correlation caused by intensity interpolation[J].Optical Engineering,2000,39(11):2915-2921.
[10]CHENG P,SUTTON M A,SCHREIER H W,et al.Full-field speckle pattern image correlation with B-spline deformation function[J].Experimental Mechanics,2002,42(3):344-352.

