基于顺序失效符的动态故障树形式规约

王 波 刘 东

(装备学院复杂电子系统仿真国防科技重点实验室，北京 101416)

李 艺

(装备学院科研部，北京 101416)

动态故障树(DFT，Dynamic Fault Tree)由静态故障树(SFT，Static Fault Tree)拓展而来.通过增加新的逻辑门，如 PAND，FDEP，CSP，WSP，HSP(本文将 CSP，WSP，HSP统称为 XSP)等，DFT提升了SFT对优先失效、储备失效和功能触发等动态特性的建模能力［1］.

DFT的研究方法主要有仿真方法和数学分析方法，本文属于后者.DFT的数学分析方法有间接法和直接法.间接法是将DFT转换为同构的状态空间模型，如时序贝叶斯网络模型(TBN，Temporal Bayesian Network)［2］、连续时间 Markov 链模型(CTMC，Continuous Time Markov Chains)［3］和随机 Petri网模型(SPN，Stochastic Petri Nets)［4］等.状态空间模型不足之处在于:①欠缺通用性;②存在指数爆炸问题.直接法是从DFT形式规约出发，构建 DFT的结构函数.DFT形式规约是将DFT动态逻辑门定义中模糊的自然语言转化成严谨的数学描述语言，从而构建DFT的严密理论体系.DFT形式规约的典型研究有Pandora法、Merle法及割序集(CSS，Cut Sequence Set)模型.Pandora法通过重新定义PAND，提出了新的逻辑门SAND和 POR［5－6］.Pandora 法能对含优先失效关系的DFT进行分析.Merle法定义了2种新的时序符号，BF(◁)和 SM(△)，提出了构建DFT结构函数的途径［7－8］.顺序失效符(SFS，Sequence Failure Symbol)“→”表示了事件发生的时序关系，LIU 通过引入 SFS，提出了 CSS模型［9］.CSS直接从基本事件的时序关系出发，给出了动态逻辑门的SFS表示方式.

本文围绕DFT形式规约，在已有方法上进行了系统研究，提出了基于SFS的DFT形式规约方式.本文主要做了3个方面的工作:①系统地、严谨地重新定义了SFS，给出了SFS性质、规则和定理，利用SFS性质定理，证明了布尔逻辑和时序逻辑的统一性;②基于SFS，提出了任意形式DFT动态逻辑门的形式规约方法;③给出了任意形式DFT动态逻辑门SFS转换的自动化算法.

1 SFS的形式框架

1.1 假 设

1)系统不可维修;

2)基本事件统计独立.

1.2 定义与性质

定义1 用“→”表示弱偏序符号SFS，“→”用于连接基本事件、静态或动态逻辑门，表示符号左边先于右边发生(即失效).

定义2 设V={v1，v2，…，vn}为含 n个元素的集合，称{vi→vj}(i，j∈{1，2，…，n})为顺序失效表达式(SFE，Sequence Failure Expression)［9］.空 SFE 表示为“∅”.SFE 有下述性质(i，j，k，l∈{1，2，…，n}):

将SFE定义拓展为{v1→v2→…→vm}(m∈{1，2，…，n})，称{v1→vj→…→vm}为长度为 m 的SFE.设给定时间t内，基本事件A的发生时间为T(A).对于基本事件 A1，A2，…，Am，{A1→A2→…→Am}的物理意义可描述为:0≤T(A1)≤T(A2)≤…≤T(Am)≤t，即 A1，A2，…，Am依次发生.同样，{v1→v2→…→vm}具有性质1)～12)，特别地，强调以下拓展性质:

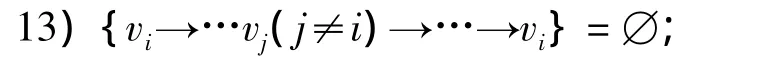
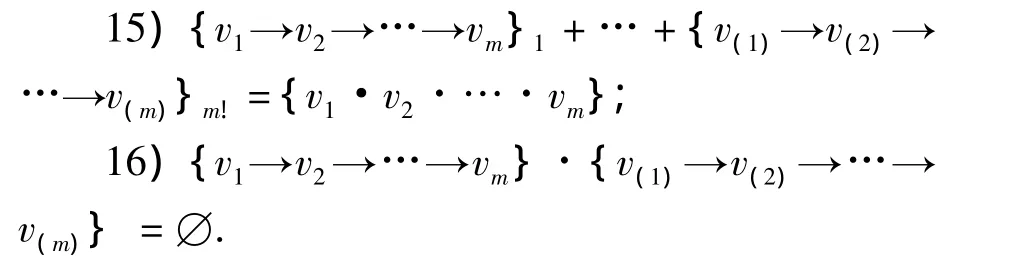
将性质16)拓展到任意2个SFE.设SFE1={v1→v2→…→vm}，SFE2={w1→w2→…→wn}，有:

定理1 相容性定理［10］.任意 1≤i1＜i2≤m，1≤j1＜ j2≤n，若 vi1=wj2，vi2=wj1，则 SFE1，SFE2是不相容的;否则是相容的.

接着介绍子集定理.先引入函数Element，其定义如下:任意 SFE={v1→v2→…→vm}，Element(SFE)={v1，v2，…，vm}，即 Element函数具有析取SFE中元素的作用，Element函数返回结果为集合.

引理1子集定理.SFE1是SFE2的子集，当且仅当 Element(SFE1)⊆Element(SFE2)，且 SFE1与SFE2是相容的.

引理2吸收定理.SFE1是 SFE2的子集，则{SFE1+SFE2}={SFE2}，{SFE2→ SFE1}={SFE2}.

至此，完成了SFS形式化框架的描述与构建.

2 SFT基于SFS的形式规约

SFT的逻辑门形式规约较简单，通常由基本事件和连接基本事件的布尔逻辑符号“∪”“∩”等组成(分别用“+”“·”替换“∪”“∩”，“·”可省略).如输入为A，B的“与门”的形式规约为A·B.将SFT所有逻辑门的形式规约整合，就得到其结构函数.结构函数沟通了基本事件和顶事件.如图1所示的SFT［11］，其结构函数可表示为

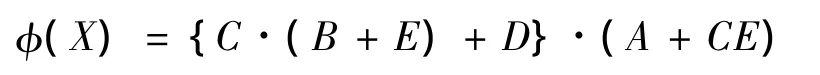
其中X表示故障树所有基本事件构成的集合.

运用布尔规则化简:

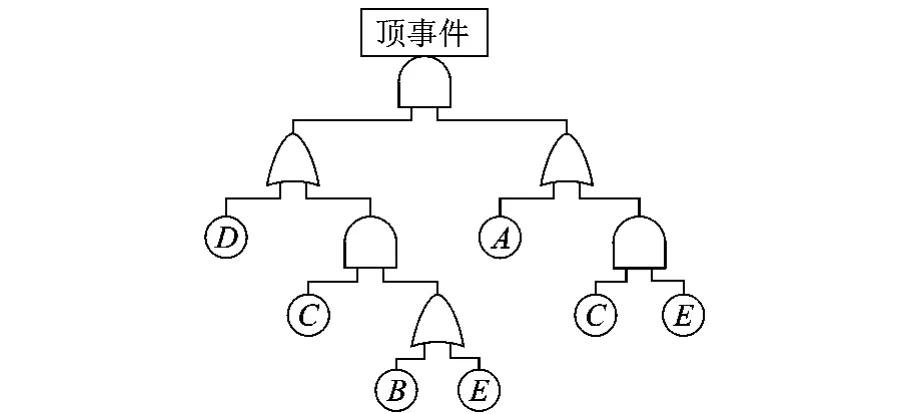
图1 SFT示意图

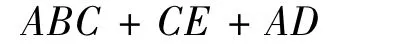
于是得到了最小割集{A，B，C}，{C，E}，{A，D}.

将SFT的结构函数转换为基于SFS代数框架的结构函数，步骤如下:

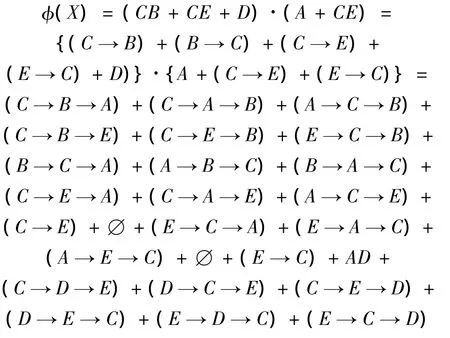
运用SFE吸收律，进一步化简，得到

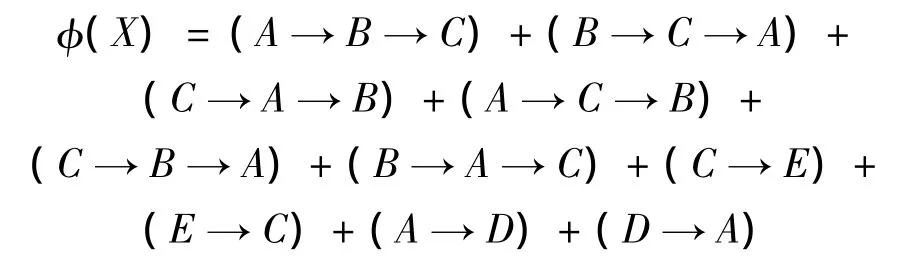
此即SFT在SFS代数框架下的形式规约.

直接利用SFE性质15)，对SFT结构函数的最简形式φ(X)=ABC+CE+AD等价转换，也可得到一致结果.由此可知，在SFS的代数框架内，SFT和DFT的形式规约是一致的，这便于将两者统一起来研究.但一般不将SFT的结构函数转换为含SFS的结构函数，因为后者形式复杂，不便于应用.

3 PAND，FDEP的SFS形式规约

DFT原始定义中包含了多种动态门，但SEQ与CSP本质上是一样的［7］，且 CSP应用范围更广，因此本文不考虑SEQ.不同动态门有不同的SFS表达方式，以下依次分析.

3.1 PAND

PAND的输出只与输入事件的发生顺序有关.在进行PAND的SFS转换时，仅需将其输入事件逐一列写.例如:PAND(A，B，C，D，E)={((((A→B)→C)→D)→E)}={A→B→C→D→E}.PAND 的形式规约在文献［5，7，9］中有较多阐述，这里不做进一步介绍.

3.2 FDEP

FDEP有1个触发事件(可以是基本事件的输入，或者其他逻辑门的输出)和多个依赖事件.依据FDEP定义，触发事件一旦发生，即使依赖事件未发生，也认为其发生，即依赖事件的失效不独立影响FDEP结果的输出.因此FEDP输出发生的情形有2种:①触发事件发生;②依赖事件发生，之后触发事件发生.

如图2所示FDEP，触发事件为T，依赖事件为A，B，C.依上述分析，其输出可以写成:

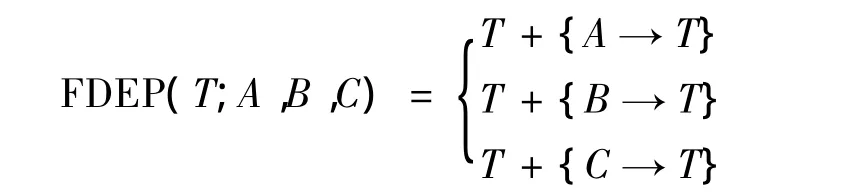
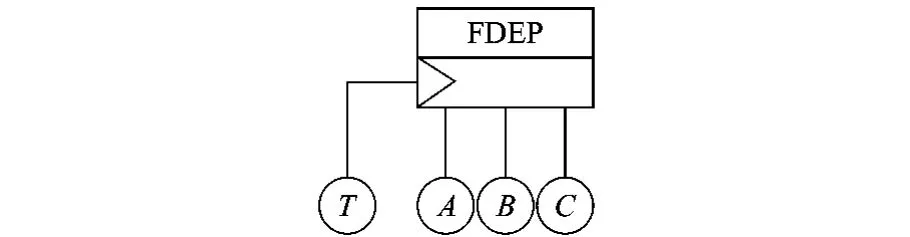
图2 FDEP示意图

然而，利用SFE性质1)，有:T={T→T};再由性质5)和引理2，有:T+{A→T}={T→T}+{A→T}={T+A}→T={T+A}.于是，FDEP输出的最简形式为

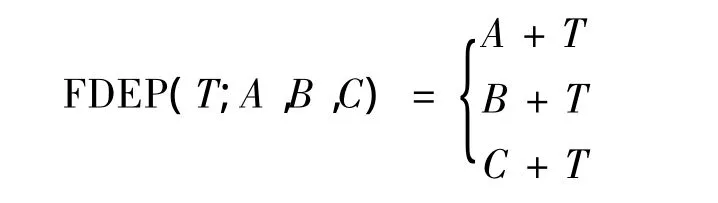
上文从理论角度给出了证明:FDEP虽然具有动态特性，但是其形式规约可等价为静态门.

再考虑一个较复杂的例子［9］.如图 3a所示的是某系统的DFT，T和A由FDEP门相连，T失效将会导致A失效，而A，B均失效时将会导致顶事件发生.该DFT实际上可以转换为图3b所示的故障树，即T，B均发生或者A，B均发生时将会导致顶事件发生.在此基础上，得到{(T→B)+(B→T)+(B→A)+(A→B)}={TB+AB}.而利用本小节阐述的方法，FDEP的输出为T+A，整个故障树的输出则为{T+A}·B={TB+AB}.

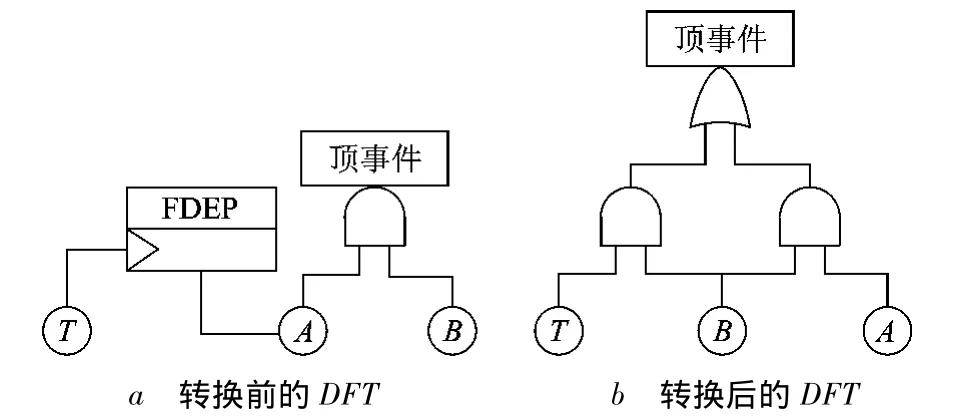
图3 FDEP的SFS转换示例

可见结果是一致的.一般地，在对FDEP门进行SFS转换时，首先将FDEP门转换为等价的静态门.

4 XSP的SFS形式规约

依据储备件的状态，备件门分为3类:CSP，WSP和HSP.文献［9］定义了睡眠因子α，α表示储备件的工作状态.当α=0时，储备件为冷储备状态，冷备件不能在储备期间失效;当α=1时，储备件为热储备状态，热备件可以在储备期间以正常失效率失效;当0＜α＜1时，储备件为温储备状态，温备件可在储备期间失效，但其失效率为正常失效率的α倍.CSP和HSP可以看成WSP的特殊情况，因此先分析WSP的 SFS形式规约.WSP门的储备件可能被其他WSP共用，先分析无共用的情况.

4.1 无共用备件的WSP

储备件有2种状态:活跃(active)和休眠(dormant).若储备件A在激活状态失效，则将其记为Aa;在休眠状态失效，则将其记为Ad［7］.再引进“独立失效”概念.独立失效是指:事件的失效与不依赖其他事件的发生［9］，如Bd→A→Ca中的事件B就发生了“独立失效”.

设WSP的n个输入事件依次为 x1，x2，…，xn，定义 f(xi)=i(i=1，2，…，n)，即将每个基本事件“绑定”一个非零自然数.转换算法如下:

1)产生n!个x1，x2，…，xn任意排列的SFEi(i=1，2，…，n);

2)任意SFEi的第1个事件(假设为X)和最后一个事件(假设为Z)分别替换为Xd，Za，如果X=x1或Z=x1，则不作替换;

3)依次检验SFEi的第2～第n－1个事件是否发生“独立失效”，若发生“独立失效”，则将其替换为xd;否则替换为xa.

例如，若WSP含有输入 A，B，C和 D，A为主件，B，C 和 D 依次为备件.{〈f(A)，f(B)，f(C)，f(D)〉}={〈1，2，3，4〉}，即 A，B，C 和 D 分别对应1，2，3和4.利用上述算法，首先得到24个SFE.任取A→C→B→D为研究对象，先用Da替换D.考虑C，f(C)＞f(B)，C发生了“独立失效”，用Cd替换C;考虑B，f(B)＜f(D)，B未发生“独立失效”，用Ba替换B.于是最终得到A→C→B→D 的 SFE:A→Cd→Ba→Da.类似地，对其他 23 个SFE进行自动化处理，可得到最终的SFE.

4.2 无共用备件的CSP和HSP

无共用备件的CSP的储备件在储备期间不能失效，所以任何储备件都不能在主件失效之前失效，而且储备件只能依次失效，因此只有1种SFE.如 CSP(A，B，C)={A→B→C}.无共用备件的HSP的储备件储备期间一直是“活跃”的，没有“休眠”状态，因此由输入事件产生的任意排列组合即为其 SFE.显然，利用 SFS性质15)容易知道，它与“与门”是等价的.

4.3 n个WSP共用1个备件

设有 n 个 WSP，WSPi(i=1，2，…，n)，每个WSP对应的主件为 xi，共用温备件 S.对于任意WSP，易知其主件失效，且其备件失效，或无可替换备件时，WSP输出产生.于是有:

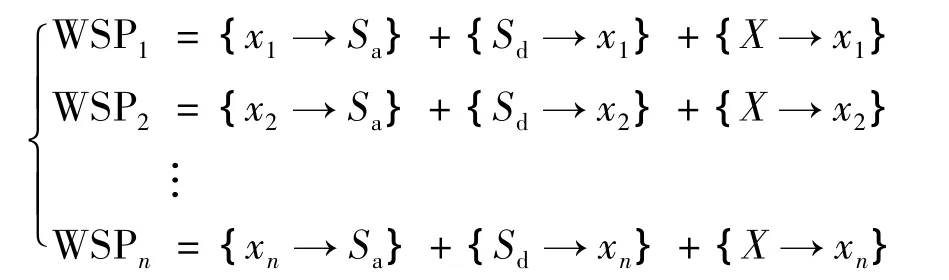
其中，X表示第1个失效的主件.

4.4 有共用备件的CSP和HSP

对于CSP，只需删掉与其同构的WSP模型中含Sd的SFE;对于HSP，同样地，将所有 Sd替换成Sa，并对新生成的SFE简化吸收即可.其他情况均可类比推导，这里不再赘述.

5 应用

利用本文方法研究HCSE(Hypothetical Computer System Example)［12］系统的形式规约，其结构如图4所示.

图4 HCSE系统结构图

HCSE系统由处理器子系统(PSF，Processing System Failure)、内存子系统(MSF，Memory System Failure)、总线子系统(BSF，Bus System Failure)及应用子系统(AF，Application Failure)等4个子系统构成(对应4个子树T1～T4).其中，PSF有2个冗余处理器A1，A2和1个冷备份处理器A，当A1，A2中任一处理器失效时，备份处理器A将替换失效处理器进行工作.A1，A2和A都是理想处理器.MSF有5个内存条，有3个正常就能保证内存系统正常.内存条通过内存接口单元与冗余总线相连，当内存接口失效时，与其连接的内存条将无法使用.M3连接了2个内存接口单元，意味着只要有1个内存接口单元正常，M3就能正常使用.BSF比较简单，仅包含2条冗余总线，冗余总线均失效才导致总线系统失效.AF考虑了操作人员OP、硬件HW和软件SW对系统的影响.操作人员通过运行在接口设备上的GUI与计算机实现连接，OP，HW和SW有一个失效就将导致系统失效.HCSE系统的DFT如图5所示.

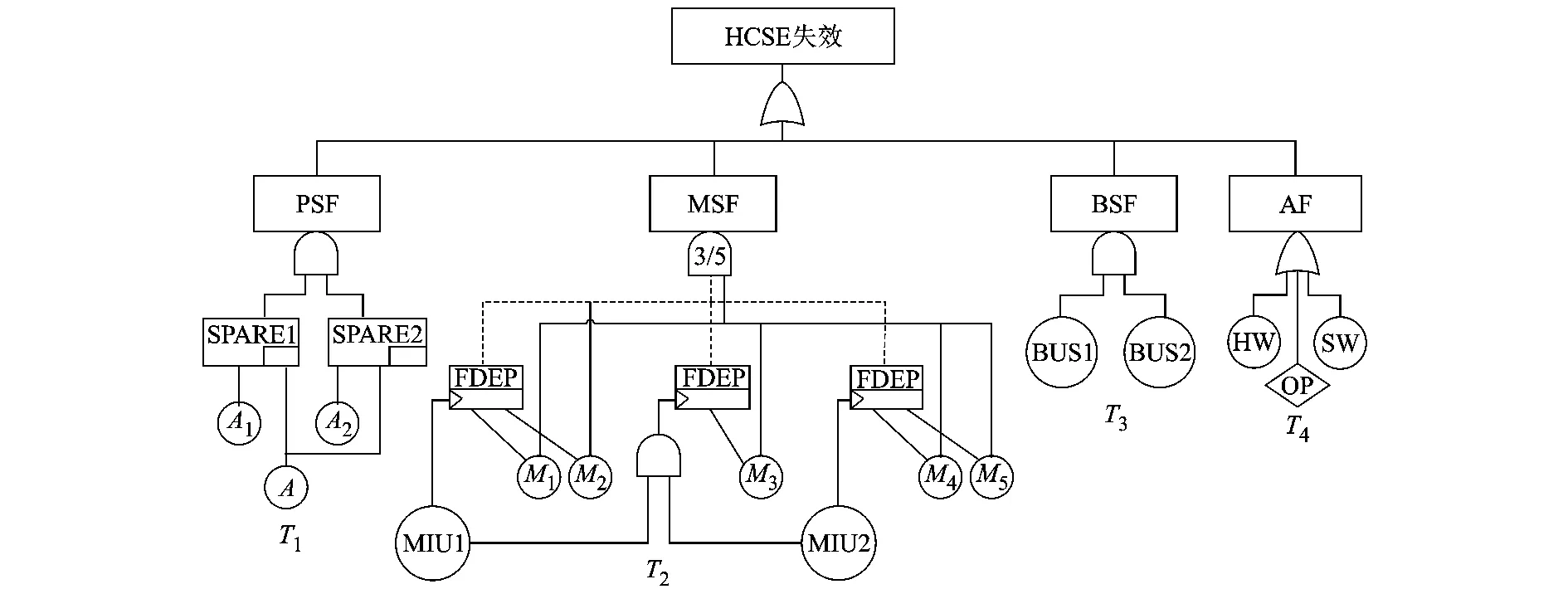
图5 HCSE的DFT

5.1 T1

由4.3 节知:

SPARE1，SPARE2的输出为逻辑“与”:

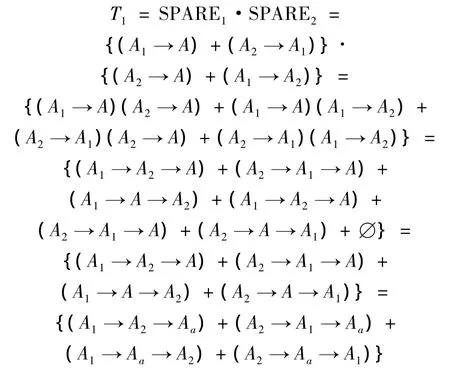
5.1.1 与 Merle 法比较

文献［7］中，首先得到

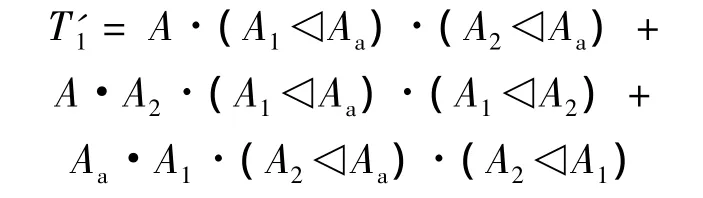
利用不交化算法，进行化简，得

往证 T1与T'1min是等价的.

证明 由 SFE性质{vi→vj}·{vj→vk}={vi→vj→vk}知:

冷备件不能在主件失效之前失效，因此上式中Aa→A1，Aa→A2是不符合实际物理意义的，于是

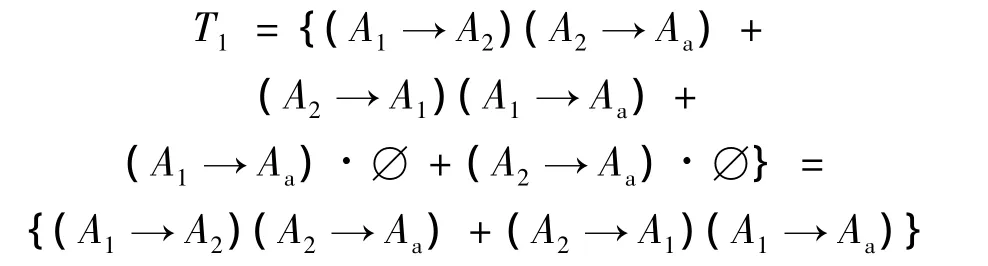
这与T'1min是一致的.

证毕

然而，Merle法中逻辑和时序混用，表意冗余、不明确;且Merle法得到的结构函数是子割序的逻辑与，并没有形成最终的割序.而本文方法直接用时序建模，将布尔逻辑和时序逻辑统一起来，含义清晰，语义无重复.利用本文提出的SFE性质定理，能直接得到最终割序.

5.1.2 与Galileo软件结果比较

Galileo软件是DFT分析的主流软件.将T1输入 Galileo 软件，得到割集结果{A，A1，A2}.这个结果包含了{A→A1→A2}和{A→A2→A1}这2个SFE，但这2个SFE是不符合物理意义的，因为冷备件A不能在主件A1，A2之前失效.究其原因，Galileo软件采用了ZBDD法［13］，该方法将所有动态门转换成了同构的“与门”，因此得到了相悖结果.而本文方法在建模粒度上较Galileo更细，也更符合实际情况.

5.2 余下子树及整个DFT

T2中含有FDEP门，已证明FDEP可以等价于静态门.因此T2～T4均可用SFT方法处理.T2～T4及整个DFT的SFS形式规约结果(TE)为

6 相关研究

Pandora法仅能对含优先失效关系的DFT进行分析，而且由于Pandora法引入的时序符号过多，相关时序表达式往往比较复杂，从而导致定性定量分析难以进行.尽管能利用约简规则对表达式化简，但欠缺规范的化简过程带来许多新问题.Merle提出了构建任意DFT结构函数的方法，但其同时考虑了基本事件之间的布尔逻辑(静态)和时序逻辑(动态)关系，如“A先于B失效”在Merle法中表示为(A·B)·(A◁B)，这种表达方式存在冗余，因此Merle提出的DFT形式规约方式并不是最优的.Rauzy［10］不考虑基本上事件之间的逻辑关系，直接从时序关系入手，改进了Merle法，但Rauzy方法仍然引进了2个时序符号，“，”和“;”，分别对应于Merle方法中的BF和SM，本质上讲，Rauzy法和Merle法是一样的;而且Rauzy并没有系统地、完整地提出DFT的形式规约方法.CSS法［9］直接从基本事件的时序关系出发，给出了动态逻辑门的SFS表示方式.CSS法是对Pandora，Merle，Rauzy 等方法的较大改进，但是 CSS法也未提出完整的DFT形式化规约方法，且过于复杂的备件门的建模方法限制了其应用.

7 结论

DFT形式规约避免了DFT基于自然语言定义的模糊性和不一致性，便于更深入理解和研究DFT，特别是产生新的DFT分析思路.基于SFS的DFT形式规约将DFT时序特性的本质给予了精确刻画，利用本文方法，可以得到任意DFT的基于SFS的形式规约.下一步研究将围绕基于形式规约的DFT量化分析展开.

References)

［1］ Dugan JB，Bavuso S，Boyd M.Dynamic fault tree models for fault tolerant computer systems［J］.IEEE Transactions on Reliability，1992，41(3):363 －377

［2］ Boudali H，Dugan JB.A continuous-time Bayesian network reliability modeling，and analysis framework［J］.IEEE Transactions on Reliability，2006，55(1):86 －97

［3］ Dugan JB，Bavuso S，Boyd M.Fault trees and Markov models for reliability analysis of fault tolerant systems［J］.Reliability Engineering and System Safety，1993，39(3):291 －307

［4］ Codetta R D.The conversion of dynamic fault trees to stochastic Petri nets，as a case of graph transformation［J］.Electronic Notes in Theoretical Computer Science，2005，127(2):45 －60

［5］ Walker M，Papadopoulos Y.Pandora:the time of priority-AND gates［C］//12th IFAC Symposium on Information Control Problems in Manufacturing(INCOM 2006).Saint-Etienne，France:IFAC，2006:237 －242

［6］ Walker M，Papadopoulos Y.Qualitative temporal analysis:towards a full implementation of the fault tree handbook［J］.Control Engineering Practice，2009，17(10):1115 －1125

［7］ Merle G.Algebraic modeling of dynamic fault trees，contribution to qualitative and quantitative analysis［D］.Paris:Lurpa，ENS de Cachan，2010

［8］ Merle G，Roussel JM，Lesage J J.Algebraic determination of the structure functions of dynamic fault trees［J］.Reliability Engineering and System Safety，2011，96(2):267 －277

［9］ Liu Dong，Xing Weiyan，Zhang Chunyuan，et al.Cut sequence set generation for fault tree analysis［C］//Proceedings of International Conference on Embedded Software and Systems.Daegu，South Korea:［s.n.］，2007:58 －69

［10］ Rauzy A B.Sequence algebra，sequence decision diagrams and dynamic fault trees［J］.Reliability Engineering and System Safety，2011，96(7):785 －792

［11］金星，洪延姬.系统可靠性与可用性分析方法［M］.北京:国防工业出版社，2007:101 Jin Xing，Hong Yanji.Methods of system reliability and availability analysis［M］.Beijing:National Defense Industry Press，2007:101(in Chinese)

［12］ Vesely W E，Stamatelatos M，Dugan JB，et al.Fault tree handbook with aerospace applications［M］.Washington DC:NASA Office of Safety and Mission Assurance，2002:157 －161

［13］ Minato S.Zero-suppressed BDDs for set manipulation in combinatorial problems［C］//Proceedings of 30th Design Automation Conference(DAC＇93).Texas:ACM/IEEE，1993:272 －277