新的导弹协同定位技术

刘俊成 张京娟

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

谭丽芬

(总装航天医学研究所，北京 100094)

当作战需求、军事理论与技术条件三者兼备之时，新的作战样式就会产生.随着信息技术，特别是无线通信技术和计算机技术的发展，战争形式由武器与武器等“平台”的对抗转变为体系与体系的对抗［1］.在这种条件下，传统导弹及其作战模式正暴露出越来越多的弊端，而导弹协同作战成为多国军方开始关注的问题.

导弹协同作战是指导弹集群通过发射平台、指挥系统及导弹之间的相互配合协作和信息交互融合，实现导弹集群战术、火力的相互支援和协调，从而达到提高导弹集群探测、跟踪和攻击等能力的目的［2］.20世纪70年代中期，美国第一次提出协同作战的概念，2002年，美国启动了“NLOSLS”(Non-Line-of-Sight Launch System)战术导弹协同作战系统的研究.俄罗斯的П-700“花岗岩”超声速反间导弹采用了领弹与攻击弹的攻击方式，也体现了导弹协同作战的概念.

导弹协同作战的关键技术之一是导弹的精确定位技术，目前导弹中制导阶段主要依靠导弹自身的惯导/GPS(Global Positioning System)组合导航定位系统进行定位，但是在战场环境下，GPS不可信赖，采用导弹集群协同定位是解决问题的途径之一.在已有的导弹协同作战的研究中，导弹协同定位方面的研究相对较少.文献［3］借鉴了多机器人协同定位的思想，采用了基于测距信息的Kalman滤波的方法，此方法要求导弹集群中至少有4枚以上位置相对精确的领弹，然后利用领弹对定位精度低的攻击弹进行协同定位.如果导弹集群中领弹少于4枚或者所有导弹精度相当，则无法利用此方法进行协同定位.针对这个问题，本文提出了一种基于相互测距信息的加权秩亏自由网平差导弹协同定位方法.

1 导弹集群协同定位原理

考虑到惯导系统的定位误差呈正态分布，因此，工作在同一位置的多套惯导通过对输出取“加权平均”的办法可明显提高其定位精度，但是，由于受惯导系统体积、重量及成本的限制，在多数情况下一枚导弹仅能装一套惯导系统，“加权平均”的思路很难实施.从“体系”的角度考虑，可以将上述思路应用到一个导弹集群.

导弹集群中的每枚导弹称为一个节点，给导弹集群的各节点配置一套弹载数据链，用于实时测量并相互通报各节点之间的距离和它们的惯导输出位置信息.由导弹各惯导提供的位置信息计算得到的弹间距离称之为计算距离.利用弹间相互测距值和计算距离之差作为量测量，根据最小二乘准则和最小加权范数准则［4］，来估计各惯导的位置误差，这样可以达到与“加权平均”类似的效果，这就是加权秩亏自由网平差协同定位技术的基本原理.

加权秩亏自由网平差是近代测量平差理论中解决秩亏自由网平差问题的一种典型方法.

2 导弹集群协同定位系统构成

2.1 系统的硬件构成

每个节点的协同定位系统都由一套弹载数据链、一套弹载惯导系统和一套弹载协同定位计算机组成.

在协同定位过程中，选取当地地理坐标系为导航系，三轴的方向分别为东向、北向和天向，本节点的惯导数据传送给弹载数据链，传输的惯导数据包括经度、纬度、高度、状态字、帧号，弹载数据链具备实时测距和通信功能，它利用无线电测距进行各节点两两之间的相互测距，同时利用无线电通信实时相互通报各节点惯导数据和相互测距信息，最终，所有节点惯导数据和相互测距信息都传送给协同定位计算机，进行协同定位计算.

作为协同定位系统的核心设备之一的弹载数据链是基于数据链技术的链路设备.美军和北约集团自20世纪60年代初开始研制数据链，根据不同时期的作战需要和技术水平，开发了一系列数据链［5－6］:Link-4，Link-10，Link-11，JTIDS(Joint Tactical Information Distribution System)，Link-22以及IFDL(Inter/Intra-Flight Data Link)等，其中JTIDS和IFDL都具有实时测距和通信功能.国内数据链的研究工作起步较晚，但发展很快，西安导航研究所、中科院空间研究所等诸多院所都对数据链展开了研究，在2005年中俄联合军演中，我军首次对外公开了天上、水面、水下的数据链系统.

2.2 测距方案和时间同步问题

数据链测距采用的是无线电测距技术.无线电测距方式有3种:单向单程测距法、双向双程测距法和双向单程测距法［7］.第1种方法要求全部节点都时间同步，后2种不需要节点之间的时间同步.

单向单程测距法，全部节点需要一个全局的同步时钟，测距过程中，节点周期性的发射带有发射时刻的无线信号，其他节点接收无线信号并测量信号到达时刻，因为全局时钟同步，所以到达时刻减去发射时刻再乘以光速即可得到节点间的距离值.单向单程测距法测距简单，测距周期短，但是，做到全局时钟同步并非易事，这需要昂贵的高精度晶振来减少钟偏和钟漂.

双向双程测距，每个节点都有自己的时钟，不需要全局的时间同步，测距过程中，通常采用“请求-应答”模式，节点向其他节点发射“请求”测距信号，其他节点接收到这个信号之后在某个时间返回“应答”信号，通过计算往返信号的时间得到节点间的距离值.但是，双向双程测距需要顺序的进行节点间相互测距，所需时间长，难以进行多节点之间同时测距，且双向双程测距设备复杂.

双向单程测距法是一种双向非相干测距方法，每个节点都有自己的时钟，不需要全局的时间同步，测距过程中，每个节点以自身时钟为基准发射单程测距信号，同时接收其他节点的单程测距信号，众节点之间可以同时进行相互测距，以节点i和j之间的相互测距为例，节点i配备的数据链设备(下面称为设备i)发射单程测距信号，同时接收其他设备的单程测距信号，设Δtij为设备i和j的时钟之间的时间不同步值，tij为设备i和j之间的无线电信号传播时间，T1为设备i测得的信号传播时间，T2为设备j测得的信号传播时间，则

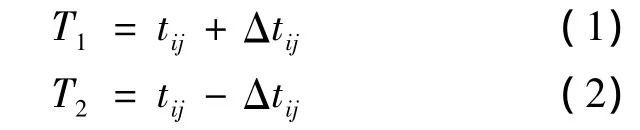
测距过程中，设备i和j工作机制完全相同，以设备i为例，设备i测得T1，同时接收设备j传输过来T2，则由式(1)和(2)计算可得

tij乘以光速即可得设备i和j的测距值.Δtij用于数据链设备之间的时间同步.

由此可见，双向单程测距法在测量距离的同时还可以测量出数据链时钟之间的时间不同步值，便于及时修正和时钟调整.因此，这种单程测距模式测距周期短且利于多节点之间同时测距.因此协同定位系统采用双向单程测距法.

双向单程测距法可以解决各数据链设备之间的时间同步问题，但是，节点i的惯导系统(下面称为惯导i)与数据链设备i之间也存在时间同步问题.因为数据链i的同步测距时刻不一定是惯导i的测量时刻，所以数据链设备i和惯导i之间有时间不同步值ΔTi.ΔTi是随机常数，如果采用100Hz输出的惯导系统，则ΔTi在±5ms以内，假设导弹飞行速度为200m/s，则ΔTi造成的距离误差在±1m以内，这个值相对惯导位置误差来说可以忽略，因此在协同定位计算过程中可以认为弹载数据链和各惯导系统之间时间同步.

3 导弹集群协同定位算法

3.1 协同定位算法的数学模型

设集群由 n 个节点组成，{xi，yi，zi}(i=1，2，…，n)为节点i的实际位置…，n)为惯导 i的输出位置1，2，…，n)为惯导i的位置误差，在弹载数据链中获得p个同步测距值.

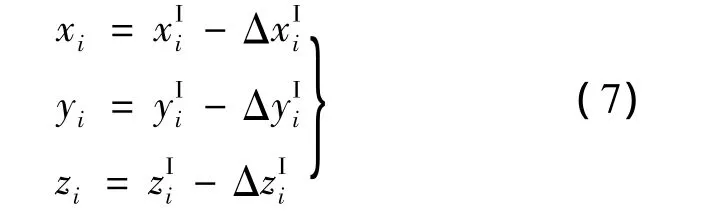
将式(7)代入式(5)并线性化，得

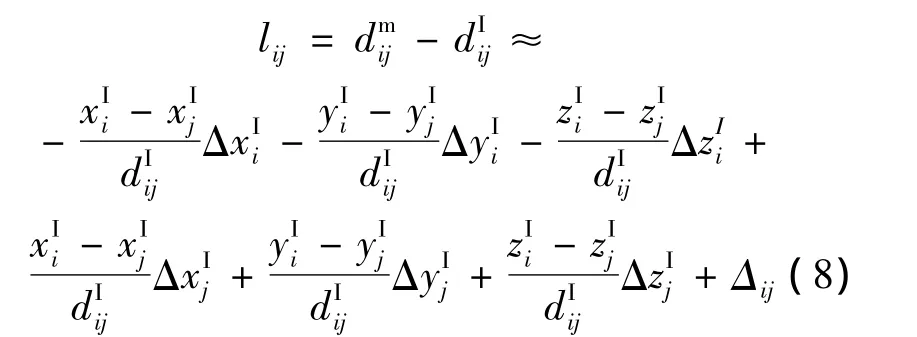
设待求参数向量X为

将式(8)写成矩阵形式为

式中，L为的p×1维量测值矩阵;H为p×3n维系数矩阵;Δ为噪声矩阵为测距值协方差矩阵.式(10)即为协同定位系统的数学模型.

为了保证式(5)的线性化误差可以忽略，采取两个措施:①利用测距值和惯导位置信息进行首个周期的组网定位计算时，要求机间距离大于惯导位置误差标准差;②利用位置误差的估计值对惯导输出进行实时闭环校正.

3.2 加权秩亏自由网平差协同定位算法

由于导弹集群所有节点都作为待定节点，没有固定节点，所以缺乏必要的起算数据，存在系数矩阵H秩亏问题，为了解决这个问题，结合测量平差理论，计算过程中采用加权秩亏自由网平差协同定位算法.

根据加权秩亏自由网平差原理［7］，为求解参数估计值选取优化指标:

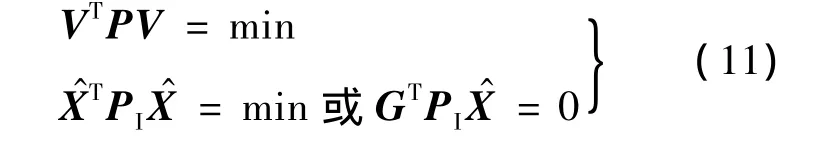
式中，V为Δ的估计值;P，PI分别为量测值权阵和惯导位置误差的权阵;矩阵G同时满足以下条件:

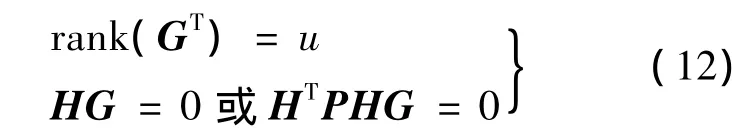
式中，rank为求秩;u为H或HTPH的秩亏数.

式(11)中，第1个优化指标为最小二乘准则，第2个优化指标为最小加权范数准则.

根据式(10)和式(11)计算得

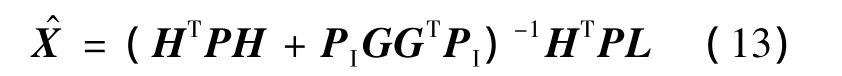
式中，当H或HTPH秩亏时，HPHT为非负定矩阵，但是PIGGTPI为正定矩阵，因此，两者的和必为正定矩阵，可以看出，加权秩亏自由网平差解决了H秩亏时求解参数估计值的问题.

如果导弹集群大致飞行在同一高度，且高度误差相对于相互测距值来说是小量，那么，可以将上述的三维加权秩亏自由网平差降阶为二维加权秩亏自由网平差.

3.3 仿真分析

仿真条件设置如下:导弹集群节点数为n，分别编号为1～n;导弹集群初始水平位置均匀分布在以坐标原点为中心，半径为1 km的圆上;导弹集群飞行高度为190m，输出的高度误差的标准差为20 m;导弹集群一直北飞，飞行速度为200m/s，航向角ψ为0;弹载数据链输出同一时刻相互测距值，测距误差的标准差为10m;导弹集群配置有相同精度的惯导系统，其陀螺随机常值漂移为0.1(°)/h，加计随机常值零偏为3×10－5g.

协同定位的计算周期取为0.1 s.因为导弹集群中所有惯导系统精度相同，所以仿真中，权值取为相等权值.仿真计算流程图如图1所示.

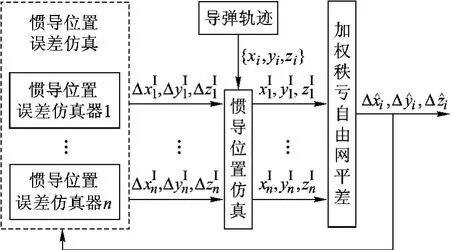
图1 仿真计算流程图

仿真结果如表1、表2和图2所示.表1是n=5时，协同定位100 s时结果.表2是n为不同值时，蒙特卡洛仿真得到的协同定位100 s时结果，设蒙特卡洛仿真次数为300次，置信水平为2，|ε|为蒙特卡洛分析结果的误差绝对值.图2是n=5时，进行协同定位100 s，惯导1位置误差、误差修正值与误差加权平均值的关系曲线和如下式:

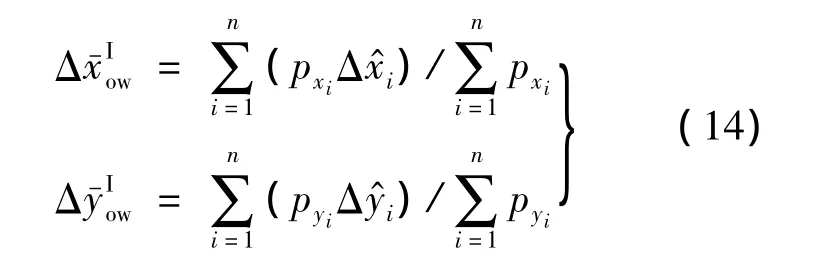
表1 协同定位仿真结果(100 s时刻)

表2 协同定位仿真结果

表2中，采用蒙特卡罗方法进行300次仿真，计算出n不同时的协同定位结果，可以看出，随着n的增大，惯导定位精度提高倍数也不断增大，当n大于4时，惯导定位精度提高了2倍以上.

图2 惯导1位置误差、修正值与误差均值(100s)

从图2中可以看出，协同定位算法有效延缓了惯导位置误差的发散速度，惯导东向和北向的位置误差修正值分别收敛于东向和北向位置误差的加权平均值附近，并分别随误差东向和北向位置误差的加权平均值的变化而变化.

4 结论

1)基于相互测距信息的导弹协同定位技术结合了导航技术和测量平差理论，从导弹集群“体系”层面出发，解决了文献［3］中所有导弹精度相当时或者领弹数量少于4枚时无法进行协同定位的问题.

2)基于相互测距信息的导弹协同定位技术有效延缓了惯导位置误差的发散速度，惯导位置修正值收敛于误差加权平均值附近，并随误差加权平均值的变化而变化.

3)基于相互测距信息的导弹协同定位技术有效地提高了惯导定位精度，且随着n的增大，惯导定位精度提高倍数也不断增大，当n大于4时，惯导定位精度提高了2倍以上.

References)

［1］ Yao Yong，Li Zhi.Research of information dissemination model based on network-centric warfare［C］//Yao Yong.Proceedings 2010 IEEE International Conference on Information Theory and Information Security.Beijing:IEEE Computer Society，2010:962－965

［2］马向玲，高波，李国林.导弹集群协同作战任务规划系统［J］.飞行力学，2009，27(1):1 －5 Ma Xiangling，Gao Bo，LiGuolin.Mission planning system of the missiles cooperative attack［J］.Flight Dynamics，2009，27(1):1－5(in Chinese)

［3］王小刚，郭继峰，崔乃刚.基于数据链的智能导弹协同定位方法［J］.中国惯性技术学报，2009，17(3):319 －323 Wang Xiaogang，Guo Jifeng，Cui Naigang.Cooperative localization approach to intelligent missile based on data link［J］.Journal of Chinese Inertial Technology，2009，17(3):319 － 323(in Chinese)

［4］黄维彬.近代测量平差理论及其应用［M］.北京:解放军出版社，1992:154－218 Huang Weibin.The principle and application of mordern survey adjustment［M］.Beijing:PLA Press，1992:154 － 218(in Chinese)

［5］ Edward K L.Air-to-ground targeting UAVs，data links and interoperability(project extender)［J］.Aeronautical Journal，2004，108(1088):493－504

［6］李宏智.战术数据链的发展与作战应用［J］.舰船电子工程，2010(4):1－5 Li Hongzhi.Development and operational applica-tion of tactical data links［J］.Ship Electronic Engineering，2010(4):1 － 5(in Chinese)

［7］ Hakyong KIM.Performance comparison of asynchronous ranging algorithms［C］//Hakyong KIM.Proceedings of IEEE Globecom 2009.Hawaii:IEEE Communications Society，2009

［8］ Lin Yiming，Chu Haibin，Qin Zizeng.GNSS autonomous navigation integrity weighted technique base on crosslink［J］.Journal of National University of Defense Technology，2010，32(5):49 －54