基于残差三阶累积量的机动检测新方法

蓝 瑶,吕泽均,姜 伟

(四川大学 计算机学院 国家空管自动化系统技术重点实验室, 成都610065)

1 引 言

在多传感器多目标跟踪系统中,当目标出现机动时,传统的卡尔曼(Kalman)滤波方法的性能会快速下降,甚至导致目标丢失,而跟踪滤波器的残差能反映目标的机动情况。因此,对残差的统计量进行检测,就能得到目标是否发生机动和发生机动的时刻,从而实时更换目标模型,提高跟踪性能。机动检测技术是基于决策的单模跟踪方法的重要模块,其目的是检测目标运动模式的变化。加权平方检测法在传统机动检测中性能较稳定,该方法通过适当调整滤波中的状态误差Q、观测误差r 及滤波估计误差方差矩阵的初始值,使得滤波器可以更准确地跟踪机动目标[1]。然而,该方法在有量测噪声的情况下,由于对高斯噪声没有滤除作用,将导致其具有较低的检测性能。多分辨率机动检测方法则可利用小波分析的多尺度分解有效地抑制噪声对目标机动的影响[2-3]。然而,由于该方法计算量大,具有较长的检测延迟,而模型的延迟更换将导致机动目标跟踪的失败。文献[4]提出一种基于高阶累积量的机动检测方法,对观测数据序列进行去均值后进行高阶累积量计算,通过二元假设检测来进行目标机动检测。虽然该方法能够抑制高斯噪声对目标机动的影响,但是对观测数据序列直接去均值减弱了数据的机动特性。

在跟踪的过程中,因为目标实际机动动态特性和所建立的目标状态模型之间的不匹配,造成了急剧变化的残差过程和目标跟踪的不准确性。残差过程统计量的变化可以应用于目标机动的检测[5]。然而任何高斯过程的高阶累积量均等于零,当加性噪声是高斯(白色或有色)噪声时,残差的高阶累积量在理论上可以滤除掉高斯噪声的影响[6]。

本文提出一种基于残差三阶累积量的机动目标检测方法,能够抑制高斯噪声(白色或有色)的影响,在信噪比较低的情况下也有较好的检测效果。

2 提出的基于残差三阶累积量的机动检测方法

根据Kalman 滤波理论,由观测量与状态预测量构成的新息残差向量为

式中,Z(k)为观测量,H X(k k -1)为状态预测量。观测量又可由目标真实状态向量HX(k)与高斯过程噪声v(k)来表示:

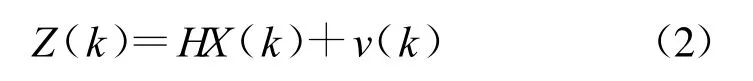
由此,式(1)可改写为

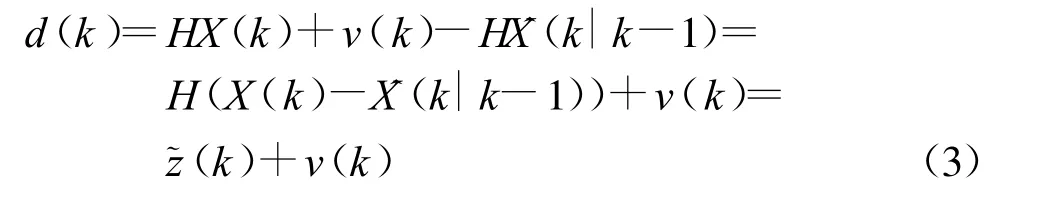
其中, z(k)=H(X(k)- X(k k -1))表示真实状态向量与状态估计向量的差值向量。

在卡尔曼滤波器中,线性最优滤波的残差序列{d(k)}为零均值高斯噪声过程。若随机过程的均值为零,则其三阶累积量与其三阶矩相等,即[6]

因为v(k)是高斯(白色或有色)噪声, 所以c3v(n,m)≡0, 则有c3d(n, m)=c3 z(n, m),其中c3 z(n ,m)为 z(k)的三阶累积量,c3v(n,m)为高斯噪声v(k)的三阶累积量。由于 c3z(n,m) 在原点取峰值[7],即

因此,零滞后的残差三阶累积量可以作为机动检测的统计检测量。如果目标发生机动,残差d(k)将不再是零均值高斯噪声过程, 其零滞后三阶累积量c3d(0,0)将不等于零,因而目标的机动检测为

基于残差三阶累积量机动检测的机动目标跟踪原理框图如图1 所示。

图1 基于残差三阶累积量机动检测的目标跟踪原理框图Fig.1 Block diagram of the maneuver detection based on residual third-order cumulants in target tracking

在实际应用中,由Kalman 滤波器得到的残差序列的三阶累积量一般不为零,因此要选取适当的门限值M>0。

长度为N 的残差数据{d(k),k =0,1, …,N-1}的三阶累积量估计则为

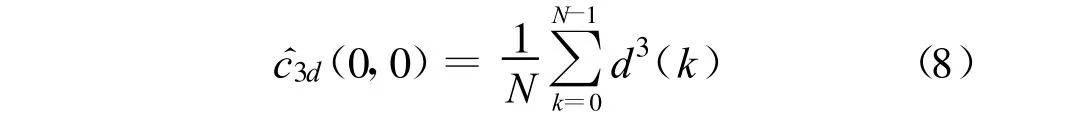
相应的检测方案为

检测门限M 的选取应依据随机变量 c3d(0,0)的概率分布确定。可将累积量进行归一化,本文采用方差法求归一化残差三阶累计量:

其中,分母中的方差可用样本平均来估计:

在数据记录足够长的情况下,统计量 c3d(0,0)渐近服从均值为零、方差为 σ2( c 3d ) E{[ c3d(0,0)-c3d(0,0)]2}的正态分布[7],即

因此,随机变量 c3d/σ2( c3d)近似为正态分布,其均值为c3d/σ2( c3d),方差为1。由此可知, c3d近似服从自由度为1 的χ2分布,其概率密度函数为

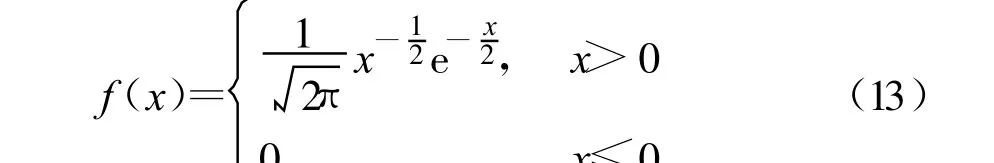
可取 c3d(0,0) 大于某一门限M 的概率为a,即

式中,a 为允许的虚警概率,可由给定的a 从χ2分布表中查得门限M。

在实际应用中,应分别对残差向量中各分量进行三阶累积量计算,再将残差分量的三阶累积量进行线性融合,并根据线性融合算法设定门限进行目标机动检测。

由假设检验的基本概念可知,判定的准确率跟样本的数量成正比:在特定的虚警概率条件下,可以通过提高样本数量来增大检测概率。但是在机动检测中,不能因为残差的累积而选择较长窗口,因为这会引起机动检测延迟的加长,从而导致增大目标状态估计误差,所以应该选择小长度窗口。但是为了每个时刻有足够的判断信息,窗口也不能选择太小,否则将明显减小检测概率,也会导致机动检测延迟的加长。由此可得,为了使检验迟延最小,一个最优长度的窗口是存在的。

在特定的虚警概率条件下,上面所述的最优滑动窗口长度可以通过里曼-皮尔森(Neyman-Pearson)准则得到。而在实际应用时一般是用数值实验方法获得。

通过Kalman 滤波对量测数据进行滤波跟踪,得到残差数据序列{d(k),k =0,1, …,N -1}。由上所述,基于残差三阶累积量的机动检测步骤如下。

步骤1:取长为N 的滑动窗,用当前第i 个残差数据最近的前N 个残差构成的序列{d(k)}的零滞后残差的分量三阶累积量,假设{d(k)}满足遍历性,则其第j 维三阶累积量的估计为

步骤2:分量残差三阶累积量的归一化。

步骤3:将残差分量的三阶累积量进行线性融合。

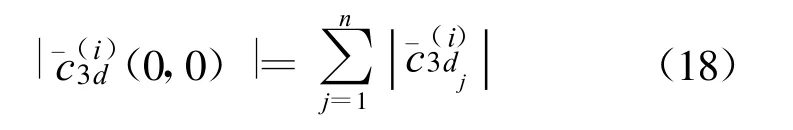
步骤4:进行门限判定。

步骤5:当残差数据更新至第i +1 个时,用当前第i+1 个残差数据最近的前N 个残差构成的序列重复以上4 个步骤,直到目标机动检测结束。

由上可知,上述机动检测方法是基于Kalman 滤波逐点获得的残差数据进行的,因此,实现了目标机动检测的实时性。

3 计算机仿真实验与分析

下面分别对加速机动和转弯机动的情况下本文算法与传统加权平方检测算法进行100 次Monte Carlo 仿真实验。

设采样周期T=1 s,观测误差是标准差为30 m的高斯色噪声。目标的初始位置为(1 000 m,1 000 m),开始沿X 、Y 轴方向飞行,初始速度分别为30 m/s、30 m/s,1 ～200 s做匀速直线运动;200 ～400 s方向转弯后做匀速直线运动, 速度分别为10 m/s、45 m/s;400 ～500 s做匀加速运动,加速度分别为2 m/s2、4 m/s2。目标的量测轨迹如图2 所示。

图2 机动目标的量测轨迹Fig.2 Maneuvering target measurement track

针对以上目标运动模型,在同等噪声环境下分别对加权平方检测算法和基于残差三阶累积量检测算法进行仿真计算。图3 和图4 分别为两种检测算法结果。

图3 加权平方机动检测方法仿真结果Fig.3 Weighted squared maneuver detection simulation results

图4 残差三阶累积量机动检测方法仿真结果Fig.4 Maneuver detection based on residual third-order cumulants simulation resu lts

由图4 可看出,跟踪目标在200 s产生的转弯机动和400 s的加速机动的检测中,残差三阶累积量机动检测效果明显,而图3 显示出传统加权平方检测算法在目标机动被噪声淹没时无法检测出机动。

从两种检测算法仿真结果可看出:在同等噪声环境下,传统加权平方检测无法通过设定门限准确地进行目标机动的检测;而相比之下,基于残差三阶累积量的机动检测能够准确检测出目标的机动,有更小的虚警和漏警,其检测概率更高;特别是在噪声严重的情况下,本文提出的新方法检测性能明显优于传统方法。

4 结 论

本文在深入研究机动目标运动特性和高斯噪声的高阶统计量性质的基础上提出了基于残差三阶累积量的机动检测算法,理论分析和Monte Carlo 仿真结果表明:在有量测噪声的环境下,与传统加权平方检测相比,该算法通过计算滤波残差的三阶累积量来滤除了高斯噪声(白色或有色)的影响,其检测性能更优。而由于通过Kalman 滤波逐点产生的残差进行有限长度的残差三阶累积量估计方法,实现了机动检测的实时性,提高了检测精度,优于多分辨率方法,是杂波环境条件下一种机动检测的可行性方法。

[ 1] 石章松,谢君.机动检测算法特性分析仿真研究[J] .计算机仿真,2007, 24(5):90-94.

SHI Zhang-song, XIE Jun.Simulation and analysis of the Characters of maneuvering diction algorithm[ J] .Computer Simulation, 2007,24(5):90-94.(in Chinese)

[ 2] Hong L.Multiresolutional estimation using wavelet transform[ J] .IEEE Transactions on Aerospace and Electronic System,1993,29(4):1244-1251.

[3] Hong L.Multiresolutional multip le-model target tracking[ J] .IEEE Transactions on aerospace and Electronic System,1994,30(2):518-524.

[4] 宋骊平, 姬红兵, 高新波.基于高阶累积量的目标机动检测新方法[ J] .电子学报,2004,32(1):154-156.

SONG Li-ping, JI Hong-bing, GAO Xin -bo.A New Method of Maneuver Detection on Higher-Order Cumulants[ J] .Acta Electronica Sinica, 2004,32(1):154-156.(in Chinese)

[5] 周宏仁, 敬忠良, 王培德.机动目标跟踪[M] .北京:国防工业出版社,1991.

ZHOU Hong-ren, JING Zhong-liang, WANG Pei-de.Maneuvering Target Tracking[M] .Beijing:National Defense Industry Press,1991.(in Chinese)

[6] Swam ia A, Giannakisb G B, Zhou G.Bibliogriaphy on higher-order statistics[ J] .Signal Processing,1997,60:65-126.

[7] Giannakis G B, Tsatsanis M K.Signal detection and classification using matched filtering and higher-order statistics[J] .IEEE Transactions on Acoustics, Speech, Signal Processing,1990, 38(7):1284-1296.

[8] 党建武, 黄建国.机动目标自适应高斯模型与跟踪算法[J] .电讯技术,2003,43(2):109-119.

DANG Jian-wu,HUANG Jian-guo.An adaptive gauss model and tracking algorithm for maneuvering target[J] .Telecommunication Engineering, 2003,43(2):109-119.(in Chinese)

[9] 范红旗,王胜, 付强.目标机动检测算法综述[ J] .系统工程与电子技术,2009,31(5):1064-1070.

FAN Hong-qi, WANG Sheng, FU Qiang.Survey of algorithms of target maneuver detection[ J] .Systems Engineering and Electroniscs, 2009, 31(5):1064-1070.(in Chinese)