同步轨道卫星四站时差统计定轨精度分析

彭华峰,郑 超,张 韬

(1.盲信号处理重点实验室,成都610041;2.西南电子电信技术研究所, 成都610041)

1 引 言

地球同步轨道(GEO)卫星的精密测定轨一直是精密测定轨领域的研究难点和热点问题,是确保高精度卫星导航、定位等的基础[1]。有源精密测距定轨方法是目前主要的精密测轨手段之一,其测轨精度可达厘米级水平[2]。光学测轨是同步卫星的主要无源测轨方式,但是容易受天气等因素影响。

基于同步卫星通信信号四站时差测量的同步卫星无源测轨方法,通过1 个中心站和3 个副站同时接收卫星通信信号,并将副站采集数据传输给主站求取时差后实现对卫星测轨。该方法具有测轨精度较高、轨道和信号直接关联等特点,为无源测轨提供了一种新的解决思路。

目前,基于四站时差测量的定位技术已经开展了相关研究,主要侧重在定位算法研究、定位精度分析以及优化布站等方面[3-7]。将四站时差定位技术应用于同步轨道卫星测轨则未见报导。因此,本文开展四站时差定位技术进行同步卫星测轨的研究,分析其统计定轨精度,对推进四站时差测轨技术的应用具有重要的指导意义。

2 四站时差无源测轨

2.1 测量原理

四站时差无源测轨是在卫星同一波束范围内的4 个测轨参考站同时接收卫星发射的同一宽带BPSK 或QPSK 通信信号。主站把接收到的信号进行解调,将解调后得到的隐含有发射时间信息的序列码及接收时间信息通过通信网络发送给各个副站,副站利用接收到的主站序列码与自己接收解调后的序列码进行相关比对,找到同源序列码及该信号到各副站的接收时间信息,这样就可以解算出卫星同源信号到达主站与3 个副站之间的时间差,从而实现对同步卫星的精确测轨。这种测轨技术有测量精度高、能全天候工作等特点。该方法的测轨原理如图1 所示。

图1 四站时差无源测轨原理示意图Fig.1 Principle figure of orbit measurement with four-station′s time difference of arrival

2.2 系统组成

同步卫星四站时差测轨系统基本组成如图2 所示,主要包括4 个接收站和1 个监控与数据处理中心。各站数据接收与采集系统主要由天伺馈系统、测轨ODU、中频矩阵和时间系统4 部分组成。

图2 四站时差无源测轨系统组成框图Fig.2 System composition of orbit measurement with four-station′s time-difference of arrival

3 统计定轨原理

3.1 动力学模型

在惯性坐标系中,应用牛顿第二定律可得人造地球卫星的运动方程如下:

式中,fTB为二体问题作用力(见文献[3-5] ,下同);f NS为地球非球形摄动力,采用JGM 3 模型;f NB为三体摄动作用力,采用JPL 的DE200 行星星历进行计算;f TD为固体潮摄动引力,同样采用JPL 的DE200行星星历进行计算;f SP为太阳光压摄动引力。

3.2 测量模型

假设卫星位置为Rs= xs,ys,zsT,4 个观测站的坐标分别为Ri= xi,yi,zi, i=0,1,2,3,其中0表示主站,其他表示副站。测量数据中通常还至少包含地面站传输线时延等系统误差,这些误差在定轨时段内可认为是较稳定的未知常值,可以在定轨同时进行估计得到,这个常值用系统误差s i(i =1,2,3)描述。则观测方程为

式中,li(i =0,1, …,3)为卫星到观测站的斜距,表达式为

观测向量对卫星位置向量的偏导数为

式中, uTi(i=0,1,2,3)为单位向量,表达式为

观测向量对系统误差的偏导数为

式中,hi中第i 个元素值为1,其他元素值为0。

3.3 迭代加权最小二乘统计定轨算法[8-11]

从前面的论述中可知,待估参数包括t 0时刻卫星的状态、系统误差等共9 个参数,用向量X0=[ x0,y0,z0,﹒x0,﹒y 0,﹒z0, s1, s2, s3]T表示。同时, 将卫星运动方程和观测方程进行线性化可得

令yi表示i 时刻的观测数据,对应的偏导数向量为Hi,权系数为wi=R-1i,则总的观测向量为y =[y1,y2, …,yn] ,权矩阵表示为W=diag(w1,w2, …,wn),偏导数矩阵为H=[ H1,H2, …,Hn]T,则方程为

则加权最小二乘的最佳估值为

通过上式估值后修正初始状态进行迭代,直至收敛:

当存在系统误差时,可以采用自校准方法进行估计,此时测量方程可表示为

式中, G 为单位矩阵,b0为系统误差向量,此时方程可转化为

式中, H′=[ H G] , X0=[ x0b0]T,方程同样通过加权最小二乘迭代估计得到卫星状态及系统误差的估计。

4 测轨精度仿真分析

4.1 仿真条件

本文采用通过Monte -Carlo 仿真方法,开展对同步轨道卫星四站时差测轨进行仿真分析。通过卫星真实星历模拟计算真实时差测量数据,然后对真实测量数据加入噪声方差为3 m即10 ns的高斯白噪声。3 m的噪声方差代表了目前所能够达到的较好的时间同步精度和测量精度水平。将仿真数据进行统计定轨后得到卫星状态估计,将其与真实星历进行比较后得到定轨误差。为比较定轨结果噪声方差分布,将上述模拟过程进行100 次Monte-Carlo 仿真,最后用100 次Monte-Carlo 定轨结果的统计方差评价定轨精度。100 次Monte-Carlo 定轨结果已经能够基本反映统计定轨的误差方差分布。定轨算法采用迭代加权最小二乘统计定轨算法,并忽略模型误差的影响。轨道计算、数据模拟及统计定轨算法均采用C#语言开发。仿真所用观测站主站位于华东地区,其余3 个副站分别位于东北、华北和华南地区。定轨弧长为1 天,测量间隔为1 min。

4.2 无系统误差时的定轨精度

通过计算机100 次Monte-Carlo 仿真得到的位置误差和速度误差如图3 所示,图中直线对应定轨误差的统计方差。从图中可以看出,当无系统误差时,统计定轨位置误差约为11 m, 速度误差约为1 mm/s。图4 给出了预报一周的位置和速度误差。从图中可以看出,预报一周后,位置误差约100 m,速度误差约8 mm/s。以上仿真结果证明四站时差测轨可以获得较高的定轨精度和预报精度。

图3 无系统误差时100 次Monte-Carlo 统计定轨误差Fig.3 The accuracy of 100 times Monte-Carlo orbit determination without system error

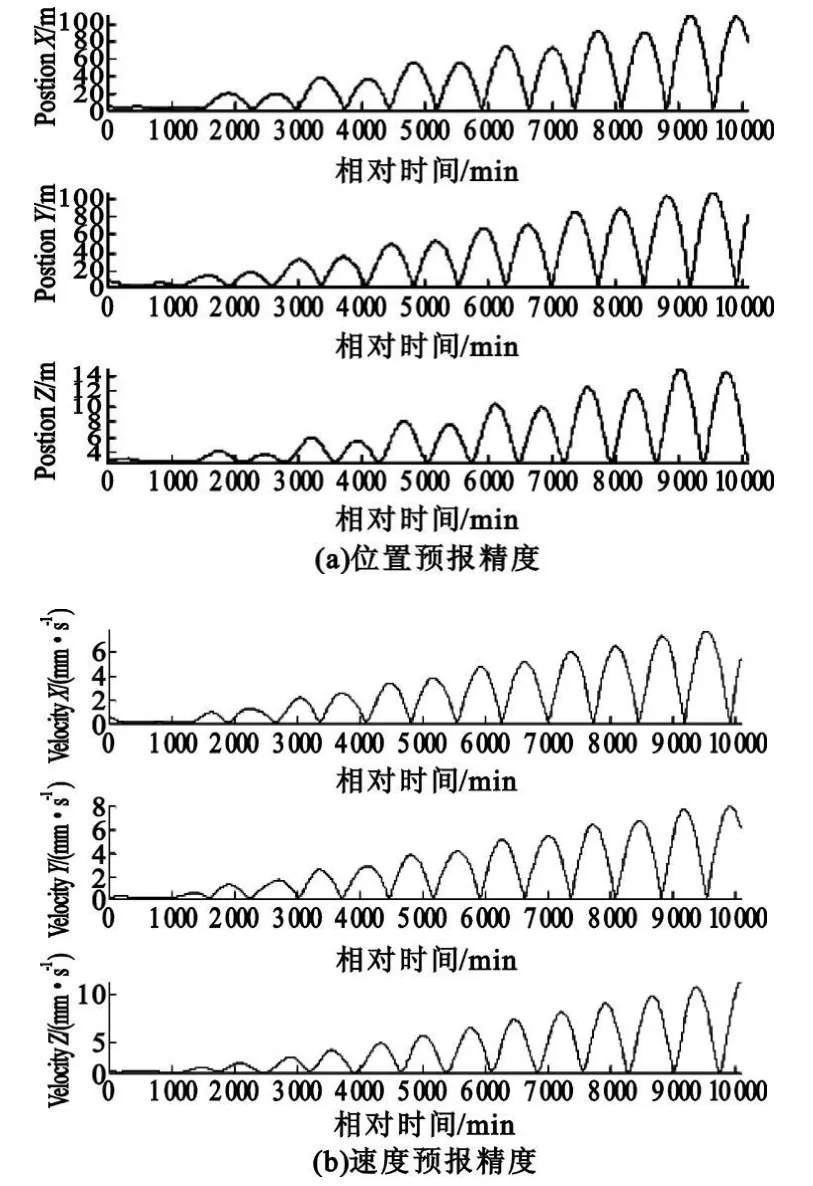
图4 无系统误差时预报1 周的误差Fig.4 The accuracy of 1-week prediction without system error

4.3 估计系统误差时的定轨精度

通过计算机100 次Monte-Carlo 仿真得到的状态误差和系统误差分别如图5 和图6 所示,图中直线对应定轨误差的统计方差。图7 为预报一周的位置和速度误差。

图5 估计系统误差时100 次Monte-Carlo 定轨误差Fig.5 The position accuracy of 100 times Monte-Carlo orbit determination with system-error estimated

图6 估计系统误差时100 次Monte-Carlo 定轨结果系统误差估计偏差Fig.6 The system-error accuracy of 100 times Monte-Carlo orbit determination with system-error estimated

图7 估计系统误差时预报1 周的轨道误差Fig.7 The orbit accuracy of 1-week prediction with system-error estimated

从图中可以看出,当有系统误差时,可以通过自校准方法估计系统误差,系统误差估计精度约为4 m/s。此时,统计定轨误差相对较大,位置误差约为120 m,速度误差约为9 mm/s,预报1 周的位置误差约为200 m,速度误差约为15 mm/s。证明存在系统误差时,仍然可以获得较高的定轨精度和预报精度。

比较有系统误差和无系统误差时的定轨结果可知,测量系统应该尽可能地消除系统误差,以便进一步提高定轨精度。

5 结 论

本文介绍了基于同步卫星信号四站时差测量的无源测轨原理,给出了该系统的基本组成,提出了基于四站时差的同步卫星自校准定轨方法。通过Monte-Carlo 仿真,重点对同步卫星的统计定轨精度进行了分析。仿真结果表明,当无系统误差时,统计定轨精度可达到11 m,1 周的预报精度约为100 m;当存在系统误差时,可通过自校准方法进行同步估计系统误差,此时定轨精度可达到120 m,1 周的预报精度约为200 m。

值得指出的是,四站时差测轨的站址布局对定轨精度影响较大,可视区内的不同卫星定轨精度可能存在较大差异,具体应用中要针对具体卫星和站址几何进行分析。有关站址几何对四站时差测轨精度影响的详细分析将另文讨论。

[1] 郭睿, 刘雁语, 谭红力, 等.基于自发自收测距的GEO卫星精密定轨[ J] .测绘科学技术学报, 2009, 26(5):333-336.

GUO Rui, LIU Yan-yu, TAN Hong-li, et al.Analysis 0f GEO Satellite Precise Orbit Determination Based on Self-Sending and Self-Receiving Ranging Data[ J] .Journal of Geomatics Science and Technology,2009, 26(5):333-336.(in Chinese)

[2] 李志刚,杨旭海,施浒立,等.转发器式卫星轨道测定新方法[ J] .中国科学G 辑,2008,38(12):1711-1722.

LI Zhi-gang, YANG Xu-hai, SHI Hu-li, et al.New Method of Satellite Orbit Survey with Transfer[ J] .Scientia Sinica(Series G),2008, 38(12):1711-1722.(in Chinese)

[3] 李建军.四星时差定位算法研究[ J] .电子对抗技术,2004,19(4):3-6.

LI Jian-jun.Research of Location Algorithm on TDOA With Four Satellites[ J] .Electronic Countermeasurement Technology,2004,19(4):3-6.(in Chinese)

[ 4] 俞志强.四站时差定位精度分析[J] .空军雷达学院学报,2010, 24(6):400-402.

YU Zhi-qiang.Analysis of 4-Station TDOA Location Accuracy[ J] .The Academic Journal of the College of Air Force,2010, 24(6):400-402.(in Chinese)

[ 5] 张政超, 童力.四站时差无源定位精度分析[J] .中国电子科学研究院学报, 2010,5(6):582-585.

ZHANG Zheng-chao, TONG Li.Precision Analysis of Passive Location of 4-stations Based on TDOA[ J] .Journal of China Academy of Electronics and Information Technology,2010,5(6):582-585.(in Chinese)

[ 6] 俞志强,王宏远, 武文.四站时差定位布站研究[J] .电子学报,2005, 33(12A):2308-2311.

YU Zhi-qiang, WANG Hong-yuan, WU Wen.4-Station Disposition Research of Position Location Using TDOA[J] .ACTA Electronica Sinica,2005,33(12A):2308-2311.(in Chinese)

[ 7] 俞志强, 叶朝谋.四站三维时差定位模糊分析[ J] .空军雷达学院学报,2009, 23(5):370-372.

YU Zhi-qiang, YE Chao-mou.Analysis of Ambiguity of 4-Station 3D TDOA Positioning[ J] .Joumal of Air Force Radar Academy,2009, 23(5):370-372.(in Chinese)

[ 8] 李济生.人造卫星精密轨道确定[M] .北京:解放军出版社,1995.

LI Ji-sheng.The satellite precision orbit determination[M] .Beijing:PLA Press,1995.(in Chinese)

[ 9] 汤锡生,陈贻迎, 朱民才.载人飞船轨道确定和返回控制[M] .北京:国防工业出版社, 2002.

TANG Xi-sheng,CHEN Yi-ying, ZHU Min-cai.Manned spacecraft orbit determination and return control[M] .Beijing:National Defense Industry Press, 2002.(in Chinese)

[ 10] 王威,于志坚.航天器轨道确定——模型与算法[M] .北京:国防工业出版社,2007.

WANG Wei,YU Zhi-jian.Spacecraft Orbit Confirm:Modeling and Algorithm [M] .Beijing:National Defense Industry Press, 2007.(in Chinese)

[11] 周庆勇, 杜兰, 蓝朝桢.基于高轨光学监视平台的定轨精度分析[ J] .光电工程, 2010,37(9):80-85.

ZHOU Qing-yong, DU Lan, LAN Chao-zhen.Analysis of of the Orbit Determination Accuracy for Space Objects Based on High-Orbit Surveillance Platform[J] .Opto-Electronic Engineering,2010,37(9):80-85.(in Chinese)