二阶多智能体系统的有限时间收敛的一致性控制

乔光耀

（南京邮电大学 自动化学院, 江苏南京 210046）

0 引言

近几年来，随着计算机技术、网络技术和通信技术的迅速发展，人们对基于多智能体系统的一致性控制的研究越来越多。多智能体系统在无人驾驶飞行器的编队控制、卫星的姿态控制、通信网络的拥塞控制等领域的广泛应用，推动着多智能体系统建模与分析的研究逐步深入。众所周知，目前在控制领域对多智能体的一致性控制的研究越来越多[1-4]。二阶多智能体系统在现实生活中具有重要的应用意义。Suiyang[5]等人提出了一种新的有限时间多面滑模观测器，最终通过误差观测器证明了多智能体网络的有限时间收敛的跟踪可以达到一个新的终端滑模面，来实现有限时间收敛。Bo Liu等人[6]建立了相同网络拓扑吸引，不同网络拓扑排斥的模型，实现了在耦合拓扑的吸引与排斥两种情况下的有限时间收敛。Feng Xiao等人[7]提出了分布式虚拟现实技术的设计，并利用李雅谱诺夫时间限定理论和代数图理论，实现了有限时间收敛。但是大多数的研究都是基于一阶多智能体网络进行研究的，而对二阶多智能体的研究则较为少见。但是二阶多智能体在现实生活中具有重要的应用意义。例如水下机器人，无人驾驶飞机都是二阶多智能体的模型。

本文针对二阶多智能体系统，基于领导-跟随模式，采用Lyapunov时间稳定性定理，给出了二阶多智能体系统有限时间收敛的条件，并且针对理论结果进行了MATLAB仿真，验证了理论结果的正确性。

1 问题的描述

假设有一个多智能体网络，具有一个领导者，n个跟随者，其中的每一个智能体都是一个二阶系统。网络的拓扑图为固定的无向强连通图。其中领导者和跟随者的动力学表达式如下：

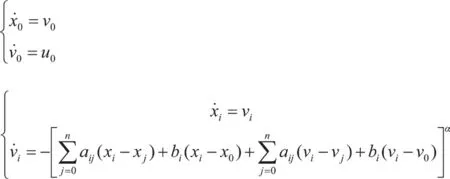
其中x0, v0, u0分别表示领导者的位置，速度与加速度状态。而xi, yi则表示跟随者的位置与速度状态。采用如下误差控制算法：

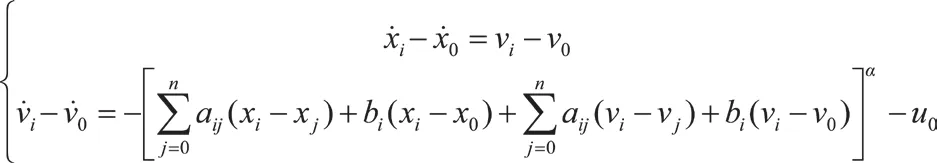
其中α是常数且0＜α＜1，x0为一时变函数。aij, i, j=1, 2,…, n是邻接矩阵A中的第（i，j）个元素。如果领导者与跟随者i之间存在信息传递，那么aij＞0, i=1, 2, …, n否则，aij=0。

2 算法描述

引理1[8]对于向量B=[b1, b2,…,bn]T≥0, B≠0，如果无向图G连通，那么矩阵L（A）+diag（B）是正定的。

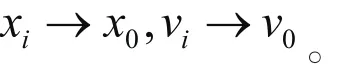
3 算法证明

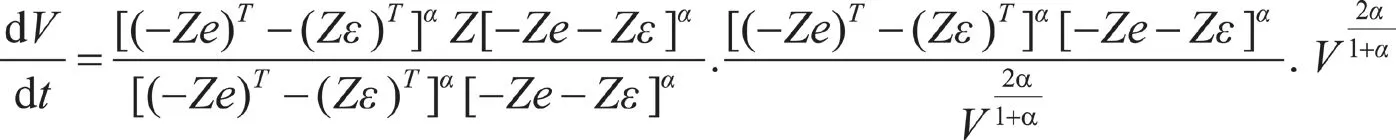
其中：

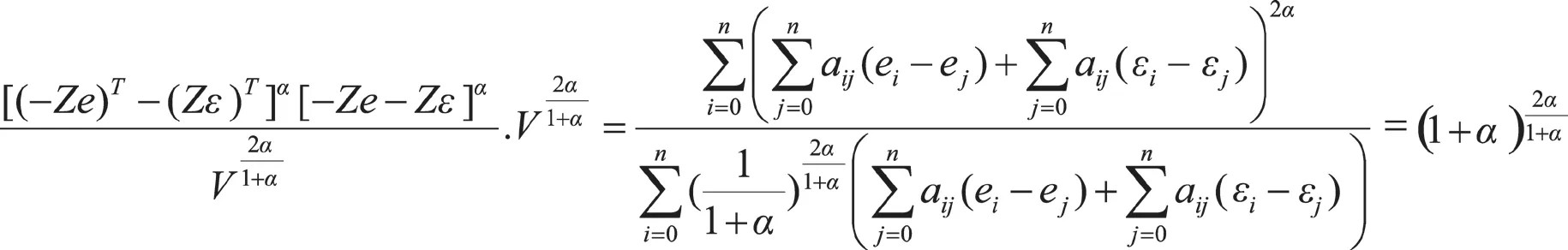
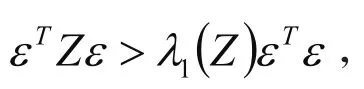
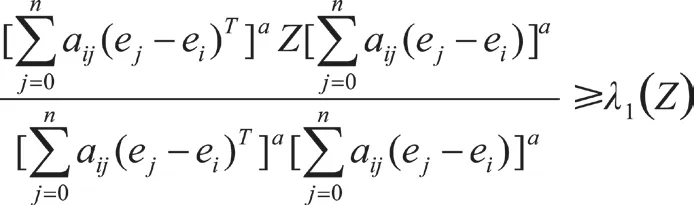
综合以上分析计算得到：

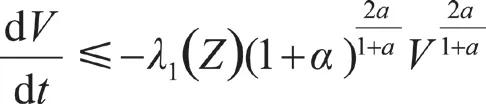
通过上述分析可以得知，该算法满足Lyapunov稳定性定理，能够在有限的时间里实现一致性收敛。

4 仿真结果

假设系统中有一个领导者L0和4个跟随者F1-F4，其通信拓扑结构图如图1所示。当智能体j在智能体i的邻域内，其邻接矩阵中的元素aij=1，否则aij=0。

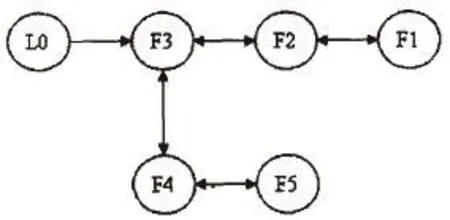
图1 仿真通信拓扑结构图

以图1的网络拓扑结构进行理论仿真，其仿真结果结果如图2所示。

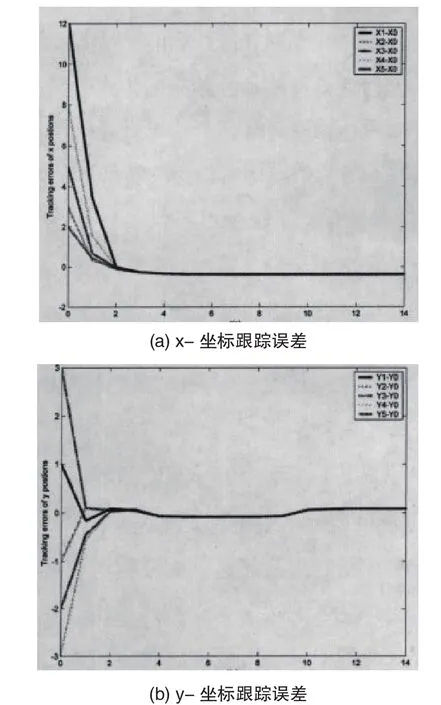
图2 仿真结果

5 小结

通过仿真结果可以得出下面结论：只要系统的网络拓扑图保持强连通，系统中的跟随者都会在一定的时间内与领导者的状态达到一致性，也就是该系统在一定的时间内实现了一致性收敛。本文的下一步工作将对时延系统的有限时间收敛的一致性控制进行研究。

[1] Vicsek T, Cziroo′k A, Ben-Jacob E, Cohen I,Shochet O.Novel type of phase transition in a system of self-deriven particles[J].Physical Review Letter,1995,75(6):1226-1229.

[2] Jadbabaie A, Lin J, and Morse A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J].IEEE Transactions Automatic Control,2003,48(6):988-1001.

[3] Olfati-Saber R and Murray R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions Automatic Control,2004,49(9):1520-1533.

[4] Fax J A.Optimal and cooperative control of vehicle formations[R].Pasadena,CA:Control Dynamical System,California Institute of Technology,2001.

[5] Suiyang,Khoo,Lihua,xie,Zhihong Man,Shengkui Zhao.Observer-based Robust Finite-time Cooperative Consensus Control for Multiagent Networks[J].Industrial Electronics and Applications,2009,30(6):1883-1888.

[6] Bo Liu,Xinmao Zhu,Jie Zhang,Yue Sun. Consensus of Multi-agent Systems Based on Leader-following Control[C].Natural Computation (ICNC), 2010 Sixth International Conference on ,2010 :1366-1370.

[7] Feng Xiao, Long Wang, Jie Chen.General Distributed Protocols for Finite-Time Consensus of Multi-Agent Systems, Decision and Control[C].2009 held jointly with the 2009 28th Chinese Control Conference,2009: 4741-4746.

[8] Wang L,Xiao F.Finit-time consensus problems for networks of dynamic angents. arXiv:math/0701724ml.