缺失投影数据的估计研究

郑源彩

（中北大学 信息探测与处理技术研究所, 太原 030051）

0 引言

CT从理论上讲是一个投影重建图像的反问题，有其普遍性，在数学界已经引起了广泛的重视。CT作为一种技术，既有坚实的数学理论为依托，又有现代微电子和计算技术相支持。目前，CT已经成为医院中不可或缺的诊断工具和科研手段，在工业各个领域也得到广泛的应用[1]。

CT图像重建算法是CT技术中较为关键的部分，CT重建算法[2]主要有滤波反投影重建算法和迭代重建算法。当投影数据完备、噪声不很严重时，滤波反投影（CBP）等解析法可以得到很好的重建图像，而且相比迭代算法速度较快，但其对投影数据的完备性要求较高，投影角度的偏少会导致明显的伪影。在实际应用中，由于考虑到剂量和对比度的因素，可能只扫描部分数据，如医用CT扫描病人；或者受条件限制不能完整扫描物体，如工业CT扫描大型飞机等不规则物体的情况，这些都属于不完全数据成像[3]。在CT扫描过程中，由于CT设备本身的结构和重建算法的局限性以及病人自主或者非自主的运动破坏了投影数据的一致性和完整性，使得我们所采集到的投影信息缺失，因此，不完全投影数据的恢复算法被人们寄予厚望[1]。在投影数据缺失，投影角度受限的情况下，常采用代数重建算法（ART）及其改进算法，但由于ART算法运行速度较慢，耗时较多[4]。从而使得将不完全角度或缺失的投影数据进行估计并恢复其投影图像是目前研究的一个难点。

在实际应用中，要克服不完全投影数据为重建算法带来的局限，就必须对不完全投影数据进行处理，使其完备化。

Kennan T.Smith于1984年首先提出了Lamda重建算法[5]，这也是研究不完全投影数据恢复领域的第一种算法，该算法的优点是具有严格的局部性，适用于重建任意维的空间信息。但是，Lamda重建算法计算过于繁琐。J.Wiegert, M.Bertram,T.Netsch等人[6]于2004年提出一种新的不完全投影数据恢复的方法，首先需要使用数学估计方法补全缺失的投影数据，然后利用数学方法对已知的不完全投影数据进行修正，但是，该方法必须要在锥角小于6度的情况下才有意义。Eric Todd Quinto[7]于2007年详细讨论了不完全数据的外部重建问题，即把物体外部视为感兴趣区域，已知该部分的投影数据，而物体内部区域的投影数据缺失的问题，并通过改进Lamda重建算法解决了这一问题。

插值方法在工程实践和科学实验中应用非常广泛，如信息技术中的图像重建、图像放大中，为避免图像的失真所做的插值补点、建筑工程的外观设计等[8]。常见的插值方法有最近邻插值法、线性插值法及三样条插值法等等。

1 投影数据估计方法

缺失投影数据的估计，目前国内外都还没有一个较好的解决方法，本文通过比较几种常用的插值方法，将其运用到缺失投影数据的估计上，并对其投影图像进行恢复，判断其恢复效果。

1.1 最近邻近插值

最近邻插值是一种简单的插值方法，它是通过计算与点P(x0, y0)临近的4个点，并将与点P(x0, y0)最近的整数坐标点(x, y)的灰度值取为P(x0, y0)点灰度近似值。在P(x0, y0)点各相邻像素间灰度变化较小时，这种方法是一种简单快捷的方法。但当P(x0, y0)点相邻像素间灰度值差异很大时，这种方法会产生较大的误差，甚至会影响图像质量，且图像有明显的锯齿状，即存在灰度不连续。

1.2 双线性插值

双线性插值法是最近邻插值法的一种改进，即用线性内插方法，根据点P(x0, y0)的4个相邻的灰度值，通过两次插值计算出灰度值。由于双线性插值法已经考虑了点P(x0, y0)的直接邻点对它的影响，因此一般可以得到令人满意的结果。但这种方法具有低通滤波性质，使高频分量受到损失，使图像细节退化而变得轮廓模糊，且该插值法计算量较大。

当在点P(x, y)处不是整数时，就要用周围点内插求出其值此时可用与之相邻的4个整数位置上的像素灰度值进行插值。待求的像素灰度计算如下：

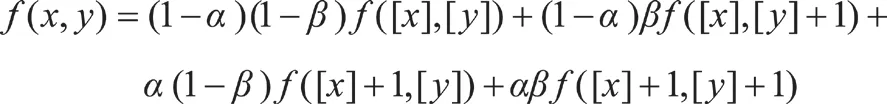
其中：α=x-[x]，β=x-[x]。

1.3 三次样条插值

为了得到更为精确的灰度值，对于角度β下的投影数据gβ，插值区间为{pβ, qβ}，对于其坐标为x的位置，三次样条插值：

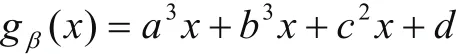
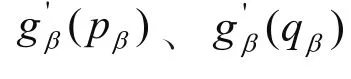
2 实验结果

采用双线性插值法对缺失的投影数据进行估计，得到不同缺失情况下的投影恢复图像。图1为标准的Sheep-Logan头部模型的投影；图2分别为缺失1列，缺失4列，以及缺失50行20列数据的投影图像；图3则是采用插值法恢复数据的投影图像。

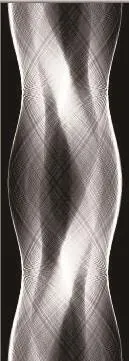
图1 Sheep-Logan头部模型投影

图2 缺失数据的投影图像

图3 恢复数据的投影图像

3 结论

通过上图可以看出尽管对缺失的投影数据进行了估计，但我们已有的先验知识并不多，还不能较精确地逼近原来的数据，因此相对应的投影图像恢复的效果也不是很好。对此，本文只是做了个初步的尝试。从图中我们可以看到对于缺失多行或者多列数据的投影进行恢复，效果不是那么好，但是对于同时缺失某几十行和某几十列数据的投影其恢复效果较前面的要好。因此，对于缺失投影数据的估计将是未来专家学者们研究的一个方向。

[1] 罗海.CT图像重建及运动伪影校正方法研究[D].合肥:中国科学技术大学,2011.

[2] 庄天戈.CT原理与算法[M].上海:上海交通大学出版社,1992.

[3] 高河伟,张丽,陈志强,程建平.有限角度CT图像重建算法综述[J].CT理论与应用研究, 2006,15(1):46-50.

[4] 王浩.CT不完全投影数据重建算法研究[D].大连:大连理工大学,2008.

[5] Smith K.T.Inversion of the X-ray transform in inverse problems[J].SIAM-AMS Proceedings, 1984:41-52.

[6] Wiegert J,Bertramb M,Wulff J et al.3D ROI imaging for cone beam computed tomography[J]. International Congress Series, 2004:7-12.

[7] Quinto E T.Local algorithms in exterior tomography[J].Journal of Computational and Applied Mathematics,2007,199(1):141-148.

[8] 赵前进.关于数值分析中插值法教学的研究[J].安徽科技学院学报,2007,21(3):34-36.