W eibull分布更新函数的指数近似算法

刘天华 张志华 李大伟 张光宇

(海军工程大学兵器工程系，武汉 430033)

W eibull分布更新函数的指数近似算法

刘天华 张志华 李大伟 张光宇

(海军工程大学兵器工程系，武汉 430033)

针对Weibull分布的更新函数较难确定的问题，研究了在平均寿命相等情况下指数分布与Weibull分布之间的贴近性.在此基础上，提出利用指数分布的更新函数模型计算Weibull分布的更新函数，能够比较方便有效地得到近似解.通过实例计算，分别比较了指数方法(直接利用指数分布的更新函数)、线性加权模型以及几何加权模型等三种方法的精度.结果表明:当时间较短时，线性加权和几何加权模型比指数方法精确度有所提高;当时间较长时，几何加权模型的精度较高.利用该结论能够为工程应用提供方便.

更新函数;指数近似;线性加权;几何加权

更新过程(renewal process)是可靠性与维修性研究领域里的一项基本理论.利用更新过程对部件或系统进行可靠性评估、可用度计算以及维修费用分析时，常常需要预测一段时间内的平均失效(更换)次数，这就涉及到更新函数(RF，Renewal Function)的确定问题.然而，对于有些常见的分布族来说，如Weibull分布、Gamma分布等，其更新函数的确定比较复杂，有时要得到明显的表达式也是比较困难的.

为此，学者们提出了一些近似方法或数值方法来计算RF.例如扩展三次样条算法(extended cubic splining algorithm)、生成函数算法(generating function algorithm)以及幂级数展开(power series expansion)等方法［1－3］.但由于实施条件复杂、具有离散化误差或者计算量过大等原因，导致这些方法未能得到广泛的应用.文献［4－5］利用累积分布函数和失效函数的线性加权或几何加权，对特征寿命内的更新函数进行近似，思路简单，精确度较高，但对于特征寿命处更新函数值的确定方法并没有明确给出，故仍然需要通过计算机模拟得到.

指数分布由于具有“无记忆性”以及与Poisson过程之间的关系，在可靠性理论与应用概率模型中有着非常重要的地位.指数分布的更新函数形式简单，在已知其平均寿命的情况下能够直接得出结果.因此，本文在研究指数分布与Weibull分布之间的紧密关系基础上，提出利用指数分布近似计算Weibull分布的更新函数.进而结合更新函数的上下限——累积失效函数和累积分布函数进行线性加权或几何加权，能够比较方便得到更新函数的近似解，最后通过模拟验证其有效性.

1 Weibull分布与指数分布的贴近性

工程中遇到的分布常常是非指数的.由于这些分布并不具有“无记忆性”，给一些定性定量分析带来了不便.很多情况下常常直接按指数分布来对待.这样处理是否具有合理性，有必要进行研究.首先需要研究这些寿命分布类的分布函数与指数分布的差异有多大.

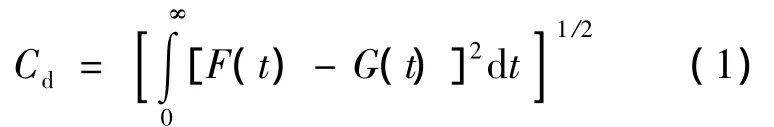
通过数值的方法评估Cd，将区间(0，1)划分成 K+1 个子区间:(0，p1)，(p1，p2)，…，(pK，1)，其中，pj=(j－0.5)/K，j=1，2，…，K.(pj，pj+1)的中间值为mj=j/K.则

这样，式(1)可以通过下式近似计算

为不失一般性，取λ=1，K=50，能够获得如图1的结果.

由图 1 可知，当 β∈(0.6，3.3)时，Cd＜0.25，此时指数分布与Weibull分布比较贴近，误差比较小.实际上进一步还能证明当β＞1，且t＜μ时，有F(t)≤G(t).

图1 Weibull分布与指数分布的逼近程度C d与β关系

2 更新函数的指数近似算法

2.1 近似思想

对于寿命分布函数为F(t)的部件，其累积失效函数(CHF，Cumulative Hazard Function)为H(t)，则其失效率函数为 r(t)=d H(t)/d t.F(t)与H(t)的关系为

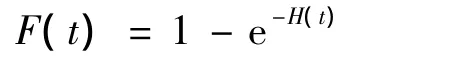
F(t)的更新函数为

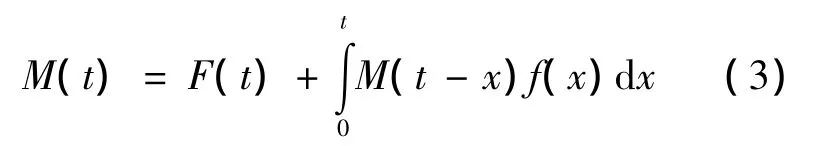
其中，f(t)=d F(t)/d t是概率密度函数.

由式(3)可知M(t)＞F(t).当t比较小时，后一项几乎等于0，则

即F(t)可以看作M(t)的下限.

类似地，由于M(t)的物理意义可以看作对于不可修产品，在完全更换条件下的平均故障次数;而H(t)可以看作在最小维修条件下的平均故障次数.显然最小维修的故障次数要大于完全替换时的故障次数，即M(t)＜H(t).当t比较小时，则有

即H(t)可以看作M(t)的上限.

由以上分析，结合M(t)的上限和下限，能够对M(t)进行近似计算.

2.2 指数近似方法

结合更新函数的上下限，采用以下两种模型近似计算 F(t)的更新函数 M(t)［4－5］.

模型1:线性加权模型

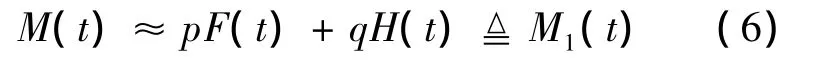
其物理意义表示［0，t)内的平均更新次数.当F(t)服从Weibull分布时，更新函数的计算是比较困难的.实际上，更新函数还有另一种表达形式，即

模型2:几何加权模型

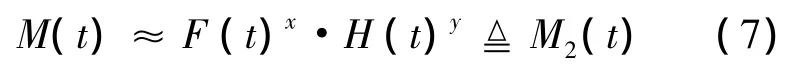
其中，p，q，x，y 是待确定参数，且满足 p+q=1，x+y=1.

在M(T)已知的情况下，联立方程组

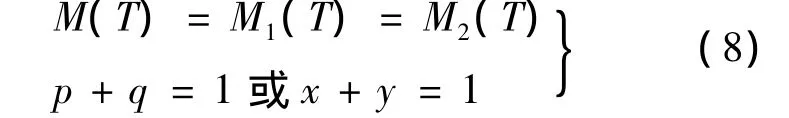
即可确定参数 p，q，x，y.从式(7)可以看出，只需要知道时刻T的更新函数值M(T)，即可利用式(5)或式(6)对时间T以内的更新函数M(t)进行近似计算.

当F(t)服从Weibull分布时，其更新函数值M(T)确定比较困难.通过前面的研究发现，在形状参数 β∈(0.6，3.3)时，平均寿命相同的指数分布与Weibull分布函数比较接近，即F(t)≈G(t).那么，当时间 T比较小时，会有 F(n)(t)≈G(n)(t).也就意味着两种分布的更新函数会比较接近.而指数分布的更新函数形式为

显然，指数分布的更新函数形式简单，容易计算.因此，利用指数分布的更新函数近似计算Weibull更新函数可以避免计算机模拟，便于工程应用.具体的计算步骤如下:

2)利用式(8)计算 p，q或 x，y;

3)利用式(6)或式(7)求得T以内的更新函数值.

3 实例分析

下面通过实例验证第2节提出的Weibull更新函数的两种指数近似方法精确性.

为方便比较，可取F(t)的平均寿命为μ=1，根据β的范围，可分别取参数为(β，λ)=(1.5，0.8577)，(2.0，0.785 4)，(2.5，0.741 5).计算T=μ=1以及T=10以内的更新函数值.首先通过模拟的方法得到精确度较高的更新函数值M(t)，然后分别采用两种模型进行近似计算，以及直接利用指数分布的更新函数式(9)(这里简称指数法)计算，结果如表1～表3所示.

从表1～表6中结果可以看出:

1)当时间在平均寿命以内时(见表1～表3)，两种近似计算模型结果与真实值比较接近，而指数方法得到的更新函数值则保守度较高;

2)当时间比较长时，大于平均寿命时(见表4～表6)，模型1即线性加权的结果会比真实值偏小，而模型2的近似效果与真实值比较接近.

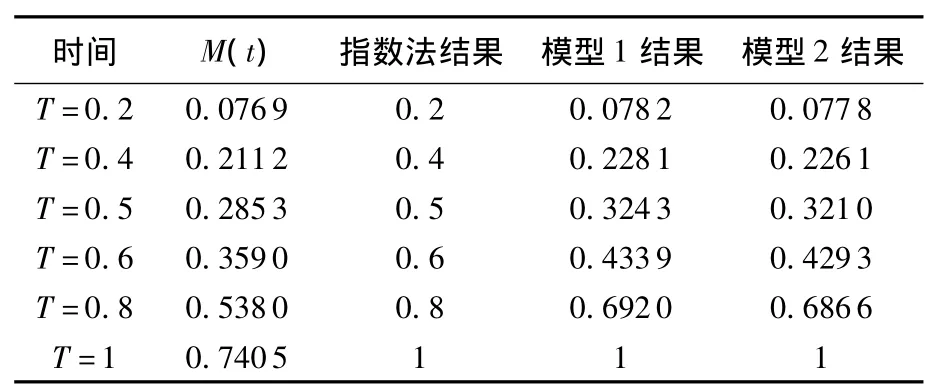
表 1 (β，λ)=(1.5，0.8577)，T=1 以内

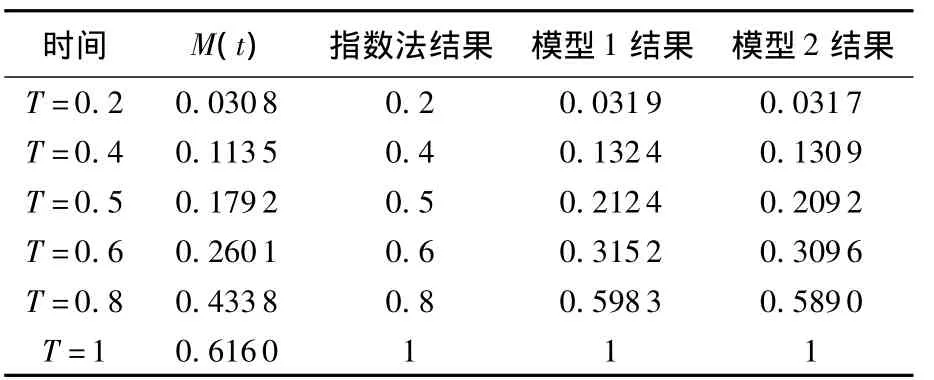
表 2 (β，λ)=(2.0，0.7854)，T=1 以内

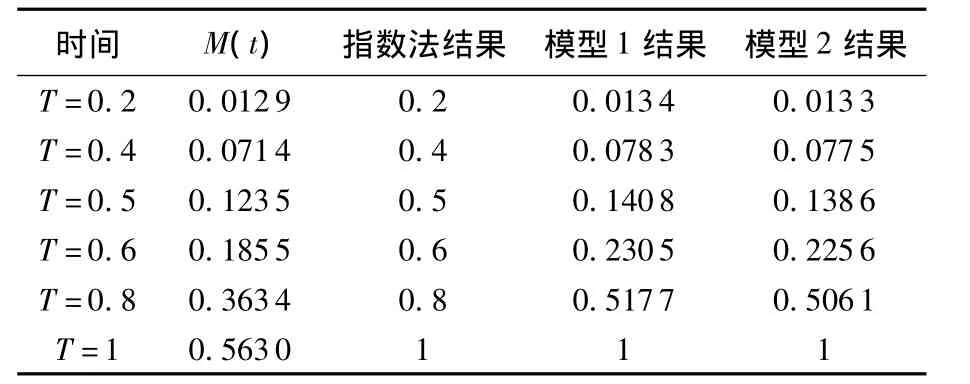
表 3 (β，λ)=(2.5，0.7415)，T=1 以内

表 4 (β，λ)=(1.5，0.8577)，T=10 以内

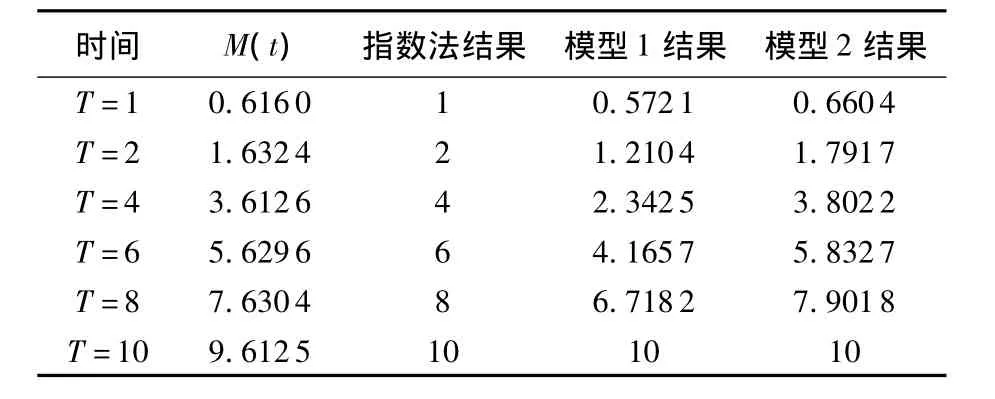
表 5 (β，λ)=(2.0，0.7854)，T=10 以内

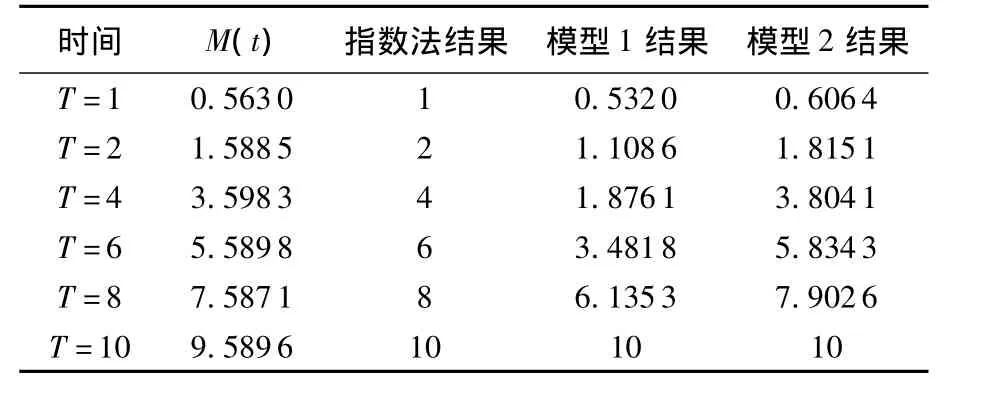
表 6 (β，λ)=(2.5，0.7415)，T=10 以内

4 结论

利用指数分布模型近似计算Weibull分布的更新函数是比较方便的，两种模型的使用时机是:①当精确度要求较低时，直接利用指数方法进行近似计算;②当精确度要求较高，且时间较短时，可利用线性加权或几何加权进行近似计算;③当精确度要求较高，且时间较长时，可利用几何加权模型进行近似计算.

类似地，对于其它分布如对数正态分布以及Gamma分布等更新函数计算比较复杂的寿命分布同样可通过指数分布的近似方法来解决.

References)

［1］ Eric Smeitink，Rommert Dekker.A simple approximation to the renewal function［J］.IEEE Transactions on Reliability，1990，39(1):71－75

［2］ McConalogue D J.Numerical treatment of convolution integrals involving distributions with densities having singularities at the origin［J］.Communications in Statistics，1981，B10:265 －280

［3］ Jiang R.A Gamma-normal series truncation approximation for computing the Weibull renewal function［J］.Reliability Engineering ＆ System Safety，2008，93:616 －626

［4］ Jiang R.A simple approximation for the renewal function with an increasing failure rate［J］.Reliability Engineering ＆ System Safety，2010，95:963 －969

［5］ Jiang R.A simple approximation for the Weibull renewal function［C］//Proceedings of the 2009 IEEE IEEM.Hong Kong:IEEE，2009:1146－1149

(编 辑:娄 嘉)

Applications of exponential-approximate method w ith multi-resolution in spare requirement determ ination

Liu Tianhua Zhang Zhihua Li Dawei Zhang Guangyu

(Dept.ofWeapon Engineering，Naval University of Engineering，Wuhan 430033，China)

As to the fact that it is difficult to determine the renewal function(RF)of the Weibull distribution，the closeness between the two distributions with the same average life was studied.On this condition，the RF of exponential distribution was applied to compute that of the Weibull distribution，and the approximate solution would be gained expediently.Furthermore，the accuracy of the three methods was compared.That is，exponential method(The RF of the exponential)，linear weight model and geometrical weight model respectively.The result shows that compared with the exponential method，the precision of the two models are highly enhanced when the time is short;and the precision of the geometrical weight model is still high when time is long.This conclusion would provide convenience for the engineering.

renewal function;exponential approximation;linearly weighted;geometrically weighted

TP 391.9

A

1001-5965(2012)06-0816-03

2011-09-23;网络出版时间:2012-06-15 15:44

www.cnki.net/kcms/detail/11.2625.V.20120615.1544.040.htm l

总装预研资助项目(51327020105，51304010206);海军工程大学博士生创新基金资助项目(HGBSJJ2011009)

刘天华(1984－)，男，湖北南漳人，博士生，111navy@163.com.