基于多核融合的目标大面积遮挡处理方法

肖 鹏 段洣毅

(北京航空航天大学 计算机学院，北京 100191)

赵 琪

(北京图形研究所，北京 100029)

基于多核融合的目标大面积遮挡处理方法

肖 鹏 段洣毅

(北京航空航天大学 计算机学院，北京 100191)

赵 琪

(北京图形研究所，北京 100029)

提出了一种基于多核融合的目标遮挡处理方法，用于提高大面积遮挡情况下视觉目标跟踪算法的鲁棒性和准确性.与现有基于单个对称核加权直方图的mean shift跟踪算法不同，该方法以目标区域内的多个非中心位置为核函数中心，构建多个非对称核加权直方图.由于这些直方图对目标的不同区域赋予了不同的权重，使得在遮挡发生时总存在一些直方图受影响较小.依据各个直方图分别进行mean shift迭代获得一组目标位置估计后，利用DS证据理论融合判定最终的目标位置.实验结果表明，该方法在目标被大面积遮挡时仍能够获得准确的跟踪.

目标跟踪;视觉跟踪;均值漂移;遮挡处理;多核;证据理论

视觉目标跟踪一直是计算机视觉领域的研究热点，在智能监控、辅助驾驶、引导打击等诸多领域都有广泛的应用.由于目标本身及周边环境复杂多变，提高视觉目标跟踪的鲁棒性依然是一个极具挑战性的课题.本文主要研究目标被遮挡情形下，尤其是大面积遮挡情形下的跟踪鲁棒性问题.核跟踪算法，又称mean shift跟踪算法，由Comaniciu［1］等人提出.该算法基于 Fukunaga［2］等人提出的非参概率密度估计算法，利用核函数加权直方图描述目标模型和候选目标，将目标定位问题转换为沿梯度方向求局部极值问题.该算法简洁实用，实时性好，近年来被广泛地研究、应用和改进.由于核函数的剖面函数具有单调递减的特性，核函数加权直方图中目标边沿点对直方图的贡献较小，目标边沿的小部分遮挡对直方图影响不大，因此核跟踪算法对部分遮挡具有一定的鲁棒性.但是，遮挡发生时核跟踪算法输出的目标位置将被“挤”向目标未被遮挡的部分，跟踪准确度有所下降，而且，如果遮挡面积过大，特别是被遮挡位置接近目标中心时，直方图将发生显著改变，跟踪往往会失败.

为此，研究者提出了多种针对遮挡问题的改进方法.这些方法大致可分为2类:基于预测的方法和基于分块的方法.基于预测的方法［3－5］引入Kalman滤波器等工具，通过目标的运动轨迹预测目标在下一帧中的可能位置，此方法可以在一定程度上防止遮挡情形下视觉特征突变引起的跟踪窗口飘离目标，但该类方法并没有改善视觉特征的匹配程度.基于分块的方法［5－7］将目标划分为若干子块，以各子块的相似度加权求和得到总的相似度函数;此类方法实际上是在一定程度上引入了目标的形状信息，可以降低部分遮挡对目标相似度判定的影响，但是当被遮挡面积过大时依然难以保证效果;而且，由于目标被划分为若干个相似的子块，跟踪过程中可能发生子块之间交叉错误关联，降低算法可靠性.

本文提出了一种基于多核融合的跟踪方法以解决目标大面积遮挡问题，该方法改变了以目标中心点为核函数中心的常规方法，而是以目标区域内的多个非中心位置为核函数中心，构建多个非对称核函数，分别进行mean shift跟踪，并利用D-S证据理论融合判定目标位置.实验结果证明该方法在目标大面积遮挡情形下仍然具有较强的鲁棒性.

1 基于多核融合的跟踪算法框架

本文提出的基于多核融合的跟踪方法如图1所示.首先，以目标区域内的多个不同点为中心，构造多个核函数，计算获得目标模型和候选区域的一组核函数加权直方图;然后，将每组对应的直方图组合用mean shift算法进行目标定位，得到一组目标位置估计及相应的相似度，再利用D-S证据理论构造mass函数，对目标位置进行融合判定，给出最终的跟踪结果.

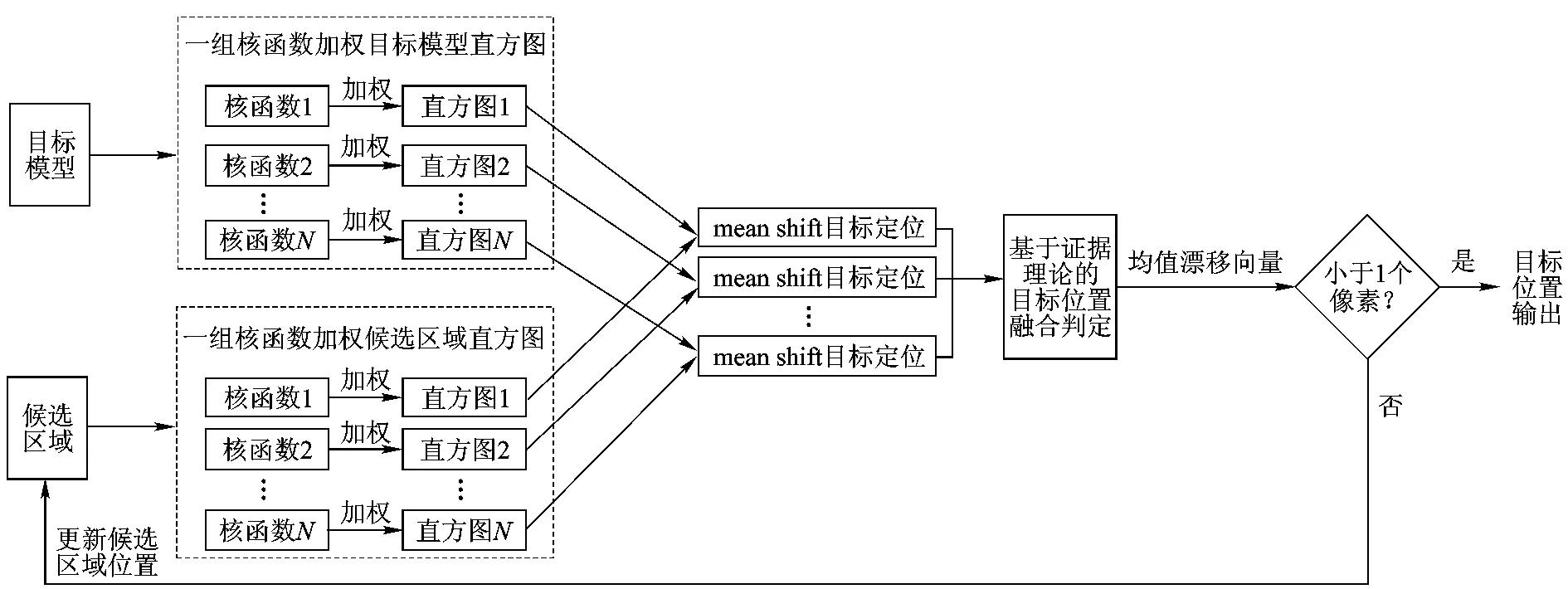
图1 算法流程图

该算法与经典的mean shift算法［1］的主要区别在于:①采用了多个而不是单个核函数.各个核函数以目标区域内的不同位置为中心，也就是说，目标中的各个像素在不同的直方图中的权重是不同的，当目标被部分遮挡时，总有某个或某些直方图受到的影响较小.②对多个跟踪结果进行了融合判定.正因为有了多个核函数，当目标被部分遮挡时，各组mean shift算法给出的目标位置必然会有较大差异，简单的平均显然得不到准确的结果，必须采用更具合理性的融合判定方法.

2 基于非对称核函数的跟踪方法

2.1 核跟踪简介

在核跟踪中，首先要提取图像的某种特征，将目标模型和候选区域以核函数加权直方图的形式表示.设目标包含 n 个像素{xi}i=1，2，…，n，区域中心为x0，特征值量化为m个等级，则目标模型可表示为

其中，k(x)为核函数对应的剖面函数，它是一个单调递减函数，使得目标中心的像素对直方图的贡献比边沿像素大;h为核函数的带宽，即目标尺度;δ为delta函数，用于判断像素xi的特征值是否属于第u个bin;C为归一化系数:

同样，包含 nh个像素{xi}i=1，2，…，nk的候选区域也表示为类似的形式:

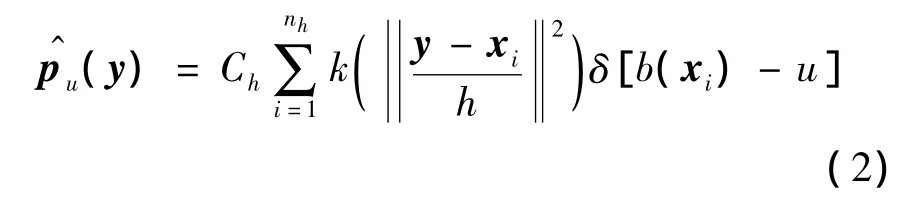
目标模型和候选区域间的相似度定义为这2个直方图的Bhattacharyya系数:

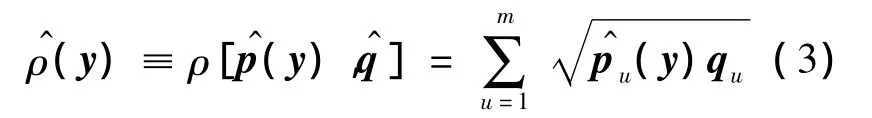
跟踪的目的就是在每帧中寻找使式(3)最大的候选区域位置.在目标的初始位置，利用Taylor展开，式(3)可以近似为

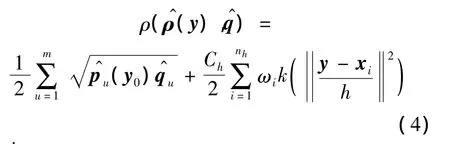
其中

式(4)中只有第2项与y有关，最大化式(4)可以通过最大化其第2项来实现，利用mean shift算法，以初始位置为起始的位移矢量可计算为

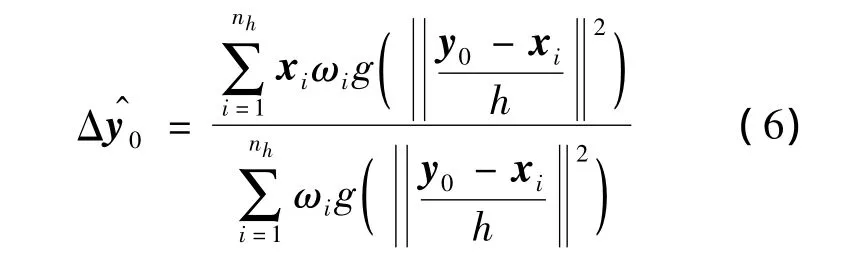
其中，g(r)=－k'(r).由于Epanechnikov核函数的剖面函数的导数为常数，故经常选用它作为核函数，式(6)可简化为

利用式(7)进行若干次迭代即可定位目标位置.

2.2 针对非对称核函数的跟踪算法修正

由于核函数的剖面函数具有单调递减的性质，核函数加权直方图中，目标边沿区域对直方图的贡献较小，边沿小部分的遮挡对直方图影响不大，因此核跟踪算法对部分遮挡具有一定的鲁棒性.但是，如果遮挡面积过大，特别是被遮挡位置接近目标中心时，直方图将发生显著改变.

如果能够将核函数中心偏移到目标区域的某一侧，则相对侧的函数值将会较低，发生在相对侧的遮挡对直方图的影响将会较小.图2所示为以灰度等级形式表示的2个核函数，图2a中核函数中心位于目标中心，图2b中核函数中心偏左上角，右下角的遮挡对直方图的影响将较小.

图2 不同中心位置的核函数

以图3所示图像为例，图3a为初始选定的目标，图3b为后续帧中被部分遮挡的目标，表1所示采用不同的核函数中心时，这2幅图像以直方图Bhattacharyya系数表征的相似性测度.

图3 原始目标及被遮挡的目标

表1 核函数中心对直方图Bhattacharyya系数的影响

可见，当目标下半部分被遮挡时，传统的以目标中心为核函数中心的直方图受影响较大，相似性测度降至0.6左右，而以左上角和右上角为核函数中心的直方图受影响较小，相似性测度依然保持0.9以上.

但是，当核函数中心与目标中心不重叠时，目标区域内的样本点分布将不对称，必须对mean shift算法进行修正.

Comaniciu［8］证明了 mean shift 算法的收敛性，即在迭代过程中，有

另一方面，随着候选区域与目标模型相似度的递增，wi将趋近于1，根据式(7)，将有

则有

由式(7)和式(9)得

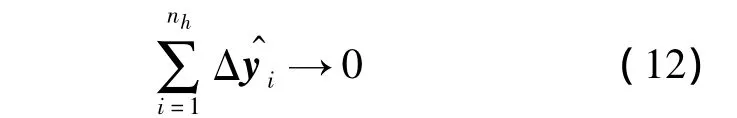
因此，在样本点不关于核函数中心对称时，只要将迭代公式修正为如下形式，也可以满足mean shift算法的收敛性.

3 基于证据理论目标位置融合判定

通过定义一组中心位置各不相同的核函数加权直方图，即可使得目标被部分遮挡时，总有某个或某些直方图受影响较小，可以相对准确的跟踪目标位置.接下来要解决的问题是如何对一组跟踪结果进行融合判定，从中选出最优的目标位置估计.

直观的想法，可以将目标模型与候选区域的相似度作为判别准则，采信相似度最高的跟踪结果.但是，实验证明这种方法往往并不能获得准确的结果.为此，本文利用基于D-S证据理论的融合判定方法.

D-S 证据理论是由 Dempster［9］和 Shafer［10］建立的一套数学理论，是对概率论的进一步扩充，是一种被广泛应用的决策级信息融合工具.D-S证据理论的特点是不仅可以对假设进行概率赋值，还可以对假设的集合进行概率赋值，通过合理设置焦元结构，可以使分辨能力强的证据在组合过程中得到更大程度的采信.

假设在跟踪中采用了N个核函数{k1，k2，…，kN}，分别利用mean shift算法，得到N个目标位置估计{l1，l2，…，lN}.建立相似度矩阵 ρ，其中 ρij表示在候选位置lj，用核函数ki加权的候选区域直方图与目标模型直方图的相似度.

对某个核函数ki，按照相似度ρij递减的顺序将相似度序列排列为{ρ(1)，ρ(2)，…，ρ(N)}，对应的目标位置序列为{l(1)，l(2)，…，l(N)}，按如下焦元结构定义一组N个mass函数:

对全部N个核函数，可得到N×N个mass函数.

在上述嵌套式的焦元结构下，分类能力强(相似度值差异大)的特征将赋予单个元素或小集合较多的概率分配，而分类能力弱(相似度值差异小)的特征将赋予大集合较多的概率分配，也就是说，特征的分类能力在概率分配上得以体现.

目标位于位置ln的概率利用D-S合成公式获得［11］:

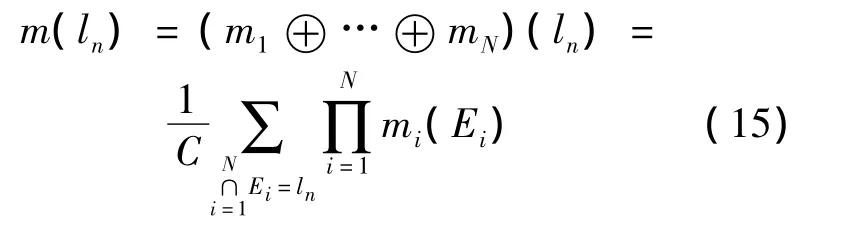
其中

概率赋值最大的目标位置即作为融合后的目标位置.

4 算法实现与实验结果

4.1 遮挡检测

显然，采用多个核函数分别进行迭代将增加计算复杂度，为此，本文设计了一种遮挡检测算法，只有在检测到遮挡发生时才启用多核融合跟踪，否则采用传统的单核跟踪方法.遮挡检测的方法如下:

定义 R=B(pak，qak)/B(pk，qk).其中 B(x，y)表示 Bhattacharyya系数;pk，qk分别表示目标模型和候选区域以常规核函数K(x)加权直方图，即目标中心部分权值较高，边沿部分权值较低;pak，qak分别表示目标模型和候选区域以1－K(x)加权的直方图，即目标中心部分权值较低，边沿部分权值较高.在正常情况下，R值应接近于1，但当目标被遮挡时，其可视面积将急剧减小，无法充满跟踪窗口，如图4所示.

图4 目标被遮挡时的跟踪窗口

此时跟踪窗口内包含大量的背景区域，R值将显著偏离于1，因此可以将|R－1|＞T作为判断遮挡的依据，其中T为预设的阈值，T值过小将增加误检率，T值过大将增加漏检率，由于漏检对跟踪准确性的影响较大，故T值设定时应以降低漏检为主要考虑因素，实验中取T=0.15.由于目标尺度变化等其它因素也可能导致R值改变，但尺度变化过程一般比较缓慢，而遮挡对目标可视面积的改变则非常迅速.因此，以当前帧跟踪窗口R值相对之前若干帧发生突变作为附加条件，以降低误检率.

4.2 跟踪算法实现

本文提出的跟踪算法与具体的视觉特征无关，为了方便算法实现和比较，采用RGB颜色直方图作为视觉特征.本文提出的以证据理论作为判别准则的多核融合跟踪算法称为MKDS(object tracking based on Multiple Kernel fusion by D-Sevidence theory);以相似度最高作为判别准则的多核融合跟踪方法称为MKLM(object tracking based on Multiple Kernel fusion by Likelihood Maximization);经典的单核mean shift跟踪算法称为SK(object tracking based on Single Kernel).

实验环境为:笔记本电脑 Thinkpad T400;CPU:Intel Core2 2.5 GHz;内存3 GB;操作系统:Windows 7 Professional;软件环境:Matlab 2009.目标初始位置以手工方式输入，跟踪结果在视频画面上以矩形框显示.

核函数选用Epanechnikov核，RGB每个颜色通道量化为8个等级，即颜色直方图共有512维.设目标宽度为w，高度为h，以目标中心位置为坐标原点，以(0，0)，(－w/2，－h/2)，(w/2，－h/2)，(－w/2，h/2)，(w/2，h/2)5 个点为中心，构建5个核函数，以目标区域内各像素距核函数中心的最大距离为核函数窗宽，分别生成5个核函数加权直方图，如图5所示.

利用证据理论对5个跟踪结果进行融合判定，选择概率赋值最大的位置作为输出.

4.3 实验结果

图5 核函数加权直方图

实验1 选择一段遮挡程度较轻的视频进行实验.实验数据为PETS2001测试集第1组中的一段(第541帧～第592帧)，视频中行人下半身被汽车遮挡，遮挡面积约占目标总面积的一半.SK，MKLM和MKDS的跟踪结果如图6所示(视频分辨率为768像素×576像素，图中只截取了每帧画面右下1/4部分).

图6可见，在第563帧目标被部分遮挡时，SK算法丢失了目标，MKLM和MKDS在后续帧中都跟住了目标.同时也可以看出，相对于MKLM算法，MKDS获得了更好的目标覆盖.分析其原因发现，由于初始选定的目标框中包含了少量背景区域，加之与目标颜色相似的背景点的影响，当遮挡发生时，简单的相似度最大原则往往不能获得最优的目标位置.如图6第2列所示，由于目标框下半部分包含的背景点较多，且行人的裤子颜色与背景相似，导致在该帧的跟踪过程中，以左下角为中心的核函数获得了最大的相似度，故MKLM算法采信了该位置;而基于证据理论的MKDS算法综合了相似度与分辨能力2项指标，获得的跟踪结果更加准确.

实验1中发生遮挡的情况下，MKDS算法的平均处理速率为0.0440 s/帧，即每秒22.73帧.

实验2 选择一段遮挡较严重的视频进行实验，视频中坦克模型被障碍物遮挡了大部分面积.视频分辨率640像素×480像素，共126帧.SK和MKDS的跟踪结果如图7所示.

可以看出，随着目标被遮挡程度不断加剧，在第77帧时SK算法丢失了目标，而本文提出的MKDS算法始终保持正确跟踪.

图8所示为跟踪过程中核函数采信情况，在初始阶段，未检测到较严重的遮挡，没有触发多核融合跟踪算法.从第65帧开始，目标下半部分遮挡逐渐加剧，MKDS算法一直采信受遮挡影响较小的左上角和右上角核函数，直至遮挡结束，获得了较好的跟踪效果.

实验2中，在发生遮挡的情况下，MKDS算法的平均处理速率为0.049 8 s/帧，即每秒20.08帧.

图6 实验1部分跟踪结果

图7 实验2部分跟踪结果

图8 跟踪过程中核函数采信情况

5 结论

针对大面积遮挡情况下的鲁棒跟踪问题，本文提出了一种多核融合的跟踪方法.该方法构造多个以不同位置为中心的核函数，分别进行mean shift迭代，使得在遮挡发生时，总存在某个或某些核函数加权直方图受影响较小，在此基础上，利用D-S证据理论，从中选出最“可信”的目标位置估计，给出准确的跟踪结果.

为了进一步提高鲁棒性和准确性，本文的方法可以与基于位置预测的遮挡处理方法结合使用，例如可以将Kalman滤波器预测的结果作为mean shift迭代的起始位置，或者将预测的结果也作为“证据”之一参与融合.此外，由于采用多核融合将显著提高计算复杂度，还可以考虑利用以往若干帧中核函数的采信情况自适应地预测下一帧中可能有效的核函数，以降低计算复杂度.后续工作中将对上述思路进行进一步研究.

References)

［1］ Comaniciu D，Ramesh V，Meer P.Kernel-based object tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25(5):564 －577

［2］ Fukunaga K，Hostetler L.The estimation of the gradientof a density function，with applications in pattern recognition［J］.IEEE Trans on Inform Theory，1975，21(1):32

［3］朱胜利.Mean Shift及相关算法在视频跟踪中的研究［D］.杭州:浙江大学电气工程学院，2006 Zhu Shengli.A study ofmean shift and correlative algorithm in Visual Tracking［D］.Hangzhou:College of Electrical Engineering，Zhejiang University，2006(in Chinese)

［4］ Wang Jiangtao，Yang Jingyu.Object tracking based on Kalmanmean shift in occlusions［J］.Journal of System Simulation，2007(9):4216－4220

［5］刘少华，张茂军，熊志辉，等.一种鲁棒高效的视频运动目标检测与跟踪算法［J］.自动化学报，2009，35(8):1055 －1062 Liu Shaohua，Zhang Maojun，Xiong Zhihui，et al.A robust and efficient video moving object detection and tracking algorithm［J］.Acta Automatica Sinica，2009，35(8):1055 － 1062(in Chinese)

［6］贾慧星，章毓晋.基于梯度方向直方图特征的多核跟踪［J］.自动化学报，2009，35(10):1283 －1289 Jia Huixing，Zhang Yujin.Multiple kernels based object tracking using histograms of oriented gradients［J］.Acta AutoMatica Sinica，2009，35(10):1283 －1289(in Chinese)

［7］颜佳，吴敏渊，陈淑珍，等.应用Mean Shift和分块的抗遮挡跟踪［J］.光学精密工程，2010，18(6):1413 －1419 Yan Jia，Wu Minyuan，Chen Shuzhen，et al.Anti-occlusion tracking algorithm based on Mean Shift and fragments［J］.Optics and Precision Engineering，2010，18(6):1413 －1419(in Chinese)

［8］ Comaniciu D，Meer P.Robustanalysis of feature space:color image segmentation［C］//Proc 1997 IEEE Conf Computer Vision and Pattern Recognition.Puerto Rico:IEEE Computer Society，1997

［9］ Dempster A P.Upper and lower probabilities induced by amultivalued mapping［J］.Annual Mathematical Statistics，1967，38(4):325－339

［10］ Shafer G.A mathematical theory of evidence［M］.Princeton，NJ:Princeton University Press，1976

［11］韩崇昭，朱洪艳，段战胜.多源信息融合［M］.北京:清华大学出版社，2006:86－88 Han Chongzhao，Zhu Hongyan，Duan Zhansheng.Multi-source information fusion［M］.Beijing:Tsinghua University Press，2006:86－88(in Chinese)

(编 辑:文丽芳)

Occlusion handling approach in visual tracking based on multiple-kernel fusion

Xiao Peng Duan Miyi
(School of Computer Science and Technology，Beijing University of Aeronautics and Astronautics，Beijing100191，China)

Zhao Qi

(Beijing Institute of Graphics，Beijing 100029，China)

A novel visual tracking approach based on multiple-kernel fusion was proposed to improve robustness and accuracy of tracking under large-area occlusion.Unlike traditional single symmetric kernel weighted histogram used in mean shift tracking，this approach adopted several asymmetric kernel functions centered at different positions within target region to build a set of asymmetric kernel weighted histograms.Because these histograms weighted each part of the target region differently，there must be some less influenced histograms during occlusion.Based on each histogram，a set of target location estimations were provided respectively by mean shift iteration，and the target location was obtained by fusing these estimations using Dempster-Shafer evidence theory.The experimental results demonstrate the effectiveness of the proposed approach under large-area occlusion.

target tracking;visual tracking;mean shift;occlusion handling;multiple kernels;evidence theory

TP 391

A

1001-5965(2012)06-0829-06

2011-03-22;网络出版时间:2012-06-15 15:43

www.cnki.net/kcms/detail/11.2625.V.20120615.1543.025.htm l

国家自然科学基金资助项目(61005084)

肖 鹏(1980－)，男，湖南长沙人，博士生，xiaopeng2010@gmail.com.