可容忍信标误差的三维传感网节点定位方法

郭晓雷 于 宁 吴银锋 万江文

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

可容忍信标误差的三维传感网节点定位方法

郭晓雷 于 宁 吴银锋 万江文

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

针对信标位置存在误差情况下的三维无线传感器网络节点定位问题，提出一种基于正交回归的多跳定位方法.同时考虑到自变量误差和因变量偏差对节点坐标估计的影响，基于约束加权正交回归参数估计准则，建立可容忍信标位置误差的三维多跳定位模型，解决了信标位置和距离估计两方面的误差并存时的节点自定位问题，并给出求解节点坐标最优值的数值方法;推导出相应的坐标估计精度评估标准3D-MCRB(3D Multi-hop Cramér-Rao Bound).仿真结果表明:此方法对信标位置误差和距离估计误差都具有较好的抑制能力，在大多数实验条件下，能将定位精度提高10%以上.

无线传感器网络;三维定位;信标位置误差;正交回归;Cramér-Rao界

无线传感器网络(WSNs，Wireless Sensor Networks)是由大量的传感器节点以无线通讯的方式组成的多跳自组织网络系统，网络化智慧感知、低成本和布置灵活的优势使其成为目前IT领域的研究热点之一［1］.在实际应用中，传感器节点通常随机部署(如飞机布撒等)在不同的环境中执行各种监测任务，自身的位置无法事先确定，因此节点在部署后首先需要实时地进行自定位.

近些年，许多学者都致力于传感网定位技术方面的研究，文献［2－3］对现有的研究成果进行了系统的综述.信标节点作为传感网定位的基础，位置坐标的准确性直接影响到整个传感网的定位性能，目前大多数经典定位算法都是在信标位置完全准确的理想条件下实现定位.然而，在实际中，由于信标节点通常依靠GPS(Global Positioning System)或人工部署的方式来获取自身的位置信息，坐标往往存在一定的不确定性，如何提高传感网定位对信标位置误差的容忍能力是一个亟需解决的重要问题.

目前针对信标位置存在误差情况下传感网定位的解决方案不多，主要有:文献［4］提出一种基于二阶锥规划的分布式定位算法，信标节点通过与邻居节点交互信息的方式，减小自身的位置误差，然而频繁的信息交换使得这种算法能耗较高;文献［5］针对传感网迭代定位中初始信标及二次信标位置存在不确定性的问题，分别利用贝叶斯和最小二乘线性估计法，以及Monte Carlo重要性采样和成本函数法，求出未知节点坐标的后验分布;文献［6］针对水下/地下传感网集中式定位问题，建立全局极大似然估计函数，采用半定规划技术实现信标位置误差独立分布条件下的所有节点定位;文献［7］通过坐标求精的方法来解决信标位置非理想条件下的传感网定位问题，在一定程度上提高了系统的定位性能.

以上方法主要集中在二维平面分析问题，大多对网络的连通性要求较高，通讯消耗较大，算法的扩展性也较差，不太适用于大规模无线传感器网络的应用.

本文从传感网分布式多跳定位的角度出发，将信标位置误差和距离估计偏差同时引入到节点坐标估计过程中，在不增加通讯消耗的基础上，利用正交回归方法增强系统对信标位置误差的容忍能力，提高传感网的定位性能.同时，给出了信标位置非理想条件下三维多跳定位的Cramér-Rao界，作为评估算法定位精度的标准.

1 问题分析

如图1所示，未知节点Nu的坐标为Xu=［xu，yu，zu］T，信标节点 Na(a=1，2，…，K)的实际坐标为 Xa=［xa，ya，za］T，声明的坐标为 X'a=［x'a，y'a，z'a］T.通过节点间直接测距和多跳信息交互，Nu可以估计出自身到信标节点Na的多跳距离d'a，距离估计误差为ea.这样，Nu的定位可以看作是如下非线性回归模型的参数估计问题:

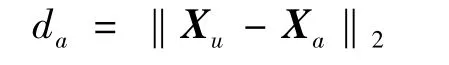
式中，Xa为自变量，其观测值为信标节点声明的坐标{X'1，X'2，…，X'K};da为因变量，其观测值为距离估计值{d'1，d'2，…，d'K}，相应的观测误差为{e1，e2，…，eK};Xu为模型的回归参数.

对于Xu的求解，通常采用非线性最小二乘法(NLSE，Nonlinear Least Squares Estimator)即

图1 节点三维定位示意图

当信标节点的坐标不存在误差，且ea服从均值为0的正态分布时，NLSE可以最大限度降低距离估计误差对节点定位的影响，是Xu的极大似然最优估计.但在实际应用中，NLSE为最优估计的前提条件并不满足，主要体现在两个方面:

1)从几何意义上讲，NLSE的目标是寻找一条(个)观测点到其垂直距离(观测方向上)平方和为最小的曲线(面)，它仅仅考虑了因变量存在的误差，未将自变量误差考虑在内.当所有变量都存在误差时，NLSE的拟合效果和稳定性都较差.在传感网节点定位中，受到GPS精度或环境干扰等影响，信标节点声明的坐标并不完全准确，如果不对其位置误差(自变量误差)进行有效处理，得到的定位结果可信度不高.

2)在多跳定位中，距离估计误差由测距误差(随机误差)和多跳折线累积误差(系统误差)共同组成，即使节点间的测距误差ε服从理想的零均值高斯分布ε～N(0，λ2)，多跳距离估计误差分布的均值也不一定为0.在ε～N(0，λ2)的条件下，统计λ分别为(2，4，6)时多跳距离估计误差的概率密度分布(PDF，Probability Distribution Function)结果如图2所示.图2验证了多跳距离估计误差近似有偏正态分布的特性.因此，在求解节点坐标时，还需要将距离估计偏差(因变量偏差)考虑在内.

图2 多跳距离估计误差概率密度分布统计图

2 正交回归方法

针对NLSE方法存在的问题，本文将信标位置误差和距离估计偏差同时引入到节点坐标估计过程中，提出一种基于正交回归的传感网多跳定位方法.

设Na声明的坐标在(x，y，z)方向上的误差(vax，vay，vaz)相互独立，均服从均值为 μa、方差为的正态分布，则Na的位置误差向量为Va=，其分布，均值向量 Ma=［μa，μa，μa］T.在多跳定位中，ea的分布规律随网络部署环境的不同而变化，设ea～，均值(距离估计偏差)b和方差都为未知数.考虑到约束加权正交回归(CWOR，Constrained Weighted Orthogonal Regression)方法可以同时降低因变量和自变量两方面的扰动对回归参数估计的影响，且有效避免局部最优值的出现，这里将其应用于信标位置误差和ea并存时的节点坐标估计中，由此建立三维无线传感器网络多跳定位模型为

当pa=qa时，式(2)的目标是寻找一个观测点到其正交距离平方和为最小的曲面，它能最小化自变量和因变量两方面误差对模型参数估计的影响，因此是一种较为理想的回归方法.

在式(2)中，目标函数包含的平方项个数为4K，回归参数个数为3K+4，而NLSE目标函数中平方项和回归参数的个数仅为K和3.相对于NLSE，CWOR模型的求解规模明显增大.如果仍采用传统的适用于NLSE的数值方法求解式(2)的最优值Z^，所需的计算量和存储量都较大.为了简化Z^的求解过程，本文参考文献［8］中数值计算的思想，对其中算法进行局部修改或简化，同时引入约束条件，得到求解信标位置非理想条件下CWOR定位模型最优值的数值方法.

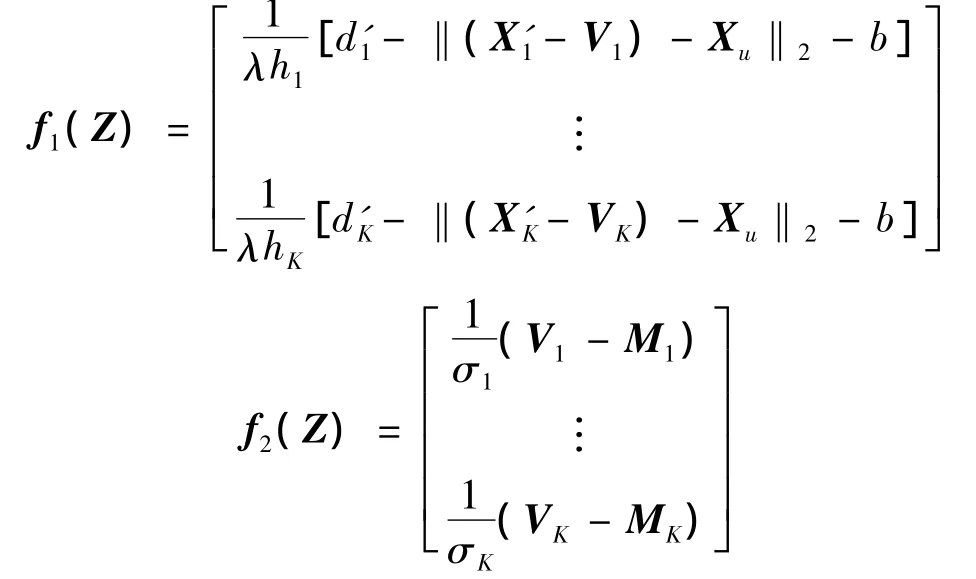
这样式(2)可以转化为

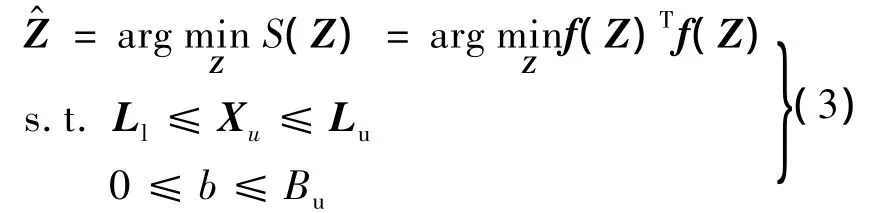
目标函数S(Z)的梯度G(Z)=2J(Z)T·f(Z)，其中J(Z)为f(Z)的Jacobian矩阵，表达式为

步骤2求 解 S(Z)的 梯 度 G(i)=2(J(i))Tf(i)，其中 J(i)=J(Z(i))，f(i)=f(Z(i)).如果‖G(i)‖2≤τ1成立(τ1为一极小门限值)，转到步骤9;否则，执行下一步.

步骤3求解一个正交矩阵Q(i)，使得

具体方法如下:

2)对J(i)a做QR分解，得到这样

4)分别取a=(1，2，…，K)，进行K次上述运算，得到所有的和

步骤4求解如下带约束条件的线性最小二乘问题，得到和Δb(i):

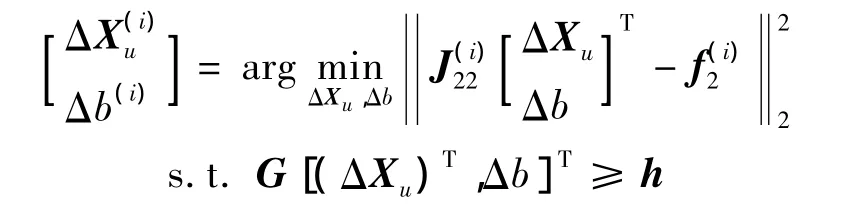
其中

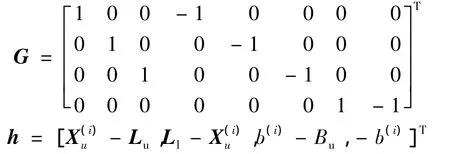
上式的求解，可以通过变量代换将其转化为最小距离规划(LDP，Least Distance Programming)问题［9］来实现.

步骤5分别取a=(1，2，…，K)，求解如下线性方程，得到所有的ΔV(i)a:

步骤6令，其中ΔZ(i)=

步骤7如果|ΔS(i)|≤τ2和‖ΔZ(i)‖2≤τ3中任意一个成立(τ2和τ3都为极小的门限值)，转到步骤9;否则，令i=i+1，转到下一步.

步骤8如果i≥Imax，转到步骤9，Imax为迭代运算的最大允许次数;否则，转到步骤2.

步骤9运算停止，输出

通过上述运算，可以得到信标位置误差和距离估计误差并存时的节点坐标估计值.

3 定位精度评估标准(3D-MCRB)

基于估计理论中的克拉美-罗界(CRB，Cramér-Rao Bound)原理给出一种评价标准，对定位精度进行评价.设，其中 Z1=是随机参数向量是非随机参数向量.这样，对于式(2)所示的多参数联合估计问题，可以采用随机和非随机参数联合无偏估计的CRB作为其估计性能的评估标准［10］.文献［5］给出了信标位置不确定条件下二维传感网迭代定位的CRB，在此基础上，本文将其推广到三维传感网多跳定位的场合，给出节点定位所能达到的误差下界3D-MCRB(3D Multihop CRB).

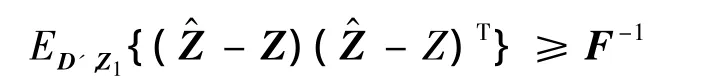
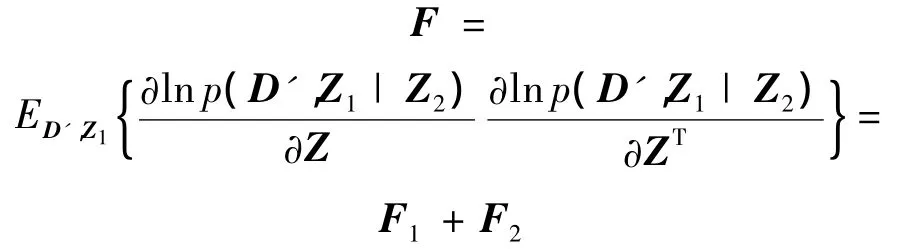
F1和F2的取值分别为

F1中的联合条件分布对数似然函数为

其相应的偏导数为

根据ED'{(D'－D －B)(D'－D －B)T}=Σ2，可得

F2表达式中的联合分布对数似然函数为

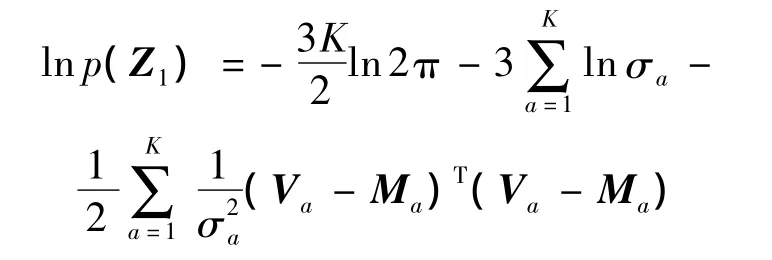
其偏导数为

于是，F2表达式中的左上角块矩阵为

通过上述推导，b无偏估计的CRB不等式为

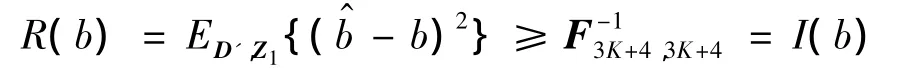
式中

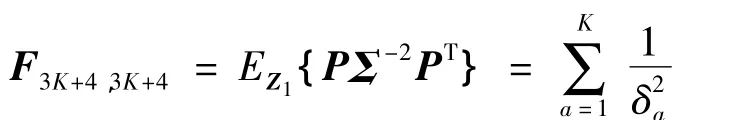
Xu无偏估计的CRB不等式为

式中

这样，通过计算I(Xu)可以推出节点坐标估计误差的下限，即信标位置和距离估计两方面的误差并存时三维传感网多跳定位所能达到的最高精度.

4 仿真实验

在200×200×200的三维空间区域内随机部署200个传感器节点，其中信标节点个数S1=20，未知节点个数S2=180.在默认条件下，网络连通度为12，节点间测距误差ε～N(0，12)，信标位置误差向量V～N(M，σ2I)，M=［μ，μ，μ］T，μ=1，σ=1.为了避免参考野值的出现，将信标节点坐标在任一方向上的误差都限制在±15之内.仿真中，相同条件下的实验都运行100次，取NLSE和CWOR两种方法的平均定位误差(ALE，Average Localization Error)与相应的3D-MCRB进行比较.ALE和3D-MCRB的计算公式如下:

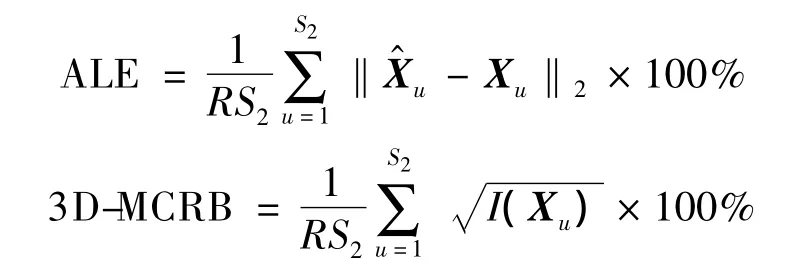
4.1 信标位置误差对定位性能的影响

分别改变信标位置误差的均值μ和标准差σ，得到两种方法的ALE和相应的3D-MCRB对比结果如图3和图4所示.随着μ增大，NLSE的ALE大致呈逐渐增长的趋势，在μ=5时，其ALE超过50%;CWOR受μ的影响较小，其ALE始终不超过30%;由于节点坐标无偏估计的CRB与μ无关，因此图3中的3D-MCRB几乎为一条直线.图4中，3条曲线都随σ的增大逐渐上升，其中NLSE的曲线变化最为明显，CWOR和3D-MCRB的变化趋势大致相同;CWOR的定位精度始终比NLSE的高14%以上，在 σ=8时甚至能达到26%.3D-MCRB显示了节点坐标无偏估计可能达到的误差下界，在两种情况下，CWOR仅比3DMCRB高10%左右.综上分析，CWOR对信标位置误差具有较强的容忍能力.

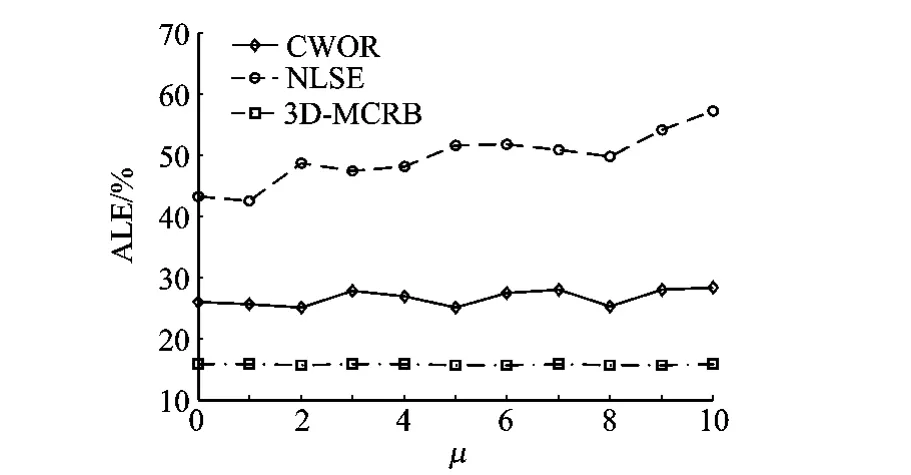
图3 信标位置误差均值对定位性能的影响

4.2 测距误差对定位性能的影响

图5为平均定位误差随测距误差标准差λ变化的关系图.在不同λ下，NLSE的ALE始终高于节点通讯半径的40%，最大为58.7%.在 λ≤6时，CWOR的ALE变化不明显，始终处于25% ～27%之间;在λ=7时，也仅为30%;继续增大λ，CWOR的ALE在λ=9时才略超过40%(仍比NLSE低13%，相应的3D-MCRB此时已经达到26%).因此，CWOR对测距误差具有一定的抑制能力，在λ不大时效果较明显.

图4 信标位置误差标准差对定位性能的影响

图5 测距误差标准差对定位性能的影响

4.3 不同网络连通度下定位性能分析

改变R，得到不同连通度下传感网定位精度对比曲线如图6所示.

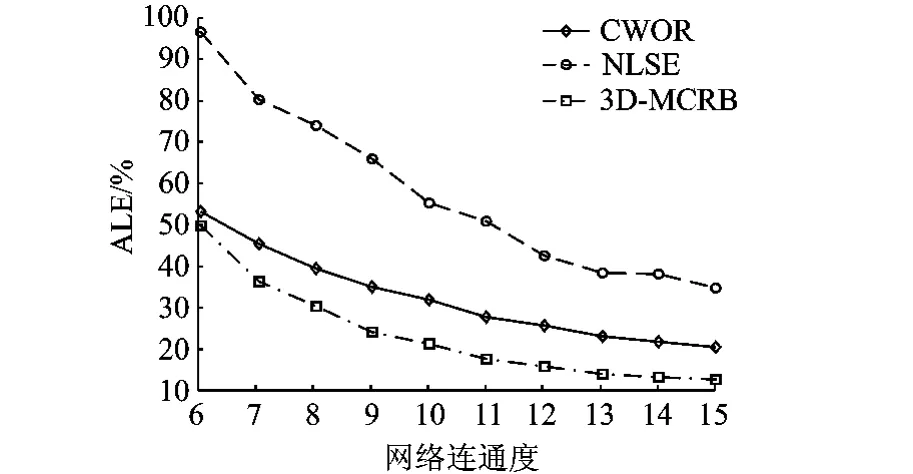
图6 网络连通度对定位性能的影响

随着网络连通度的增大，不相邻节点间的最短路径接近直线的概率增大(多跳折线累积误差减小)，同时未知节点在信息帧生命周期(TTL，Time To Live)范围内可以获得的参考信息数量增加，因此两种方法的ALE都呈逐渐下降的趋势.在网络连通度较小时(不大于9)，相对于NLSE，CWOR能够显著提高传感网的定位精度(超过30%)，其ALE接近3D-MCRB;在网络连通度为15时，CWOR仍能将定位精度提高约14%.

5 结论

由于信标位置的不确定性和多跳距离估计的有偏性，节点自定位时需要将自变量误差和因变量偏差同时考虑在内.本文给出一种适用于大规模三维无线传感器网络的节点多跳定位方法，采用正交回归技术，最小化信标位置和距离估计两方面的扰动对节点坐标估计的影响，增强传感网定位系统的容错性能.在大多数实验条件下，相对于非线性最小二乘法，CWOR能将定位精度提高10%以上，定位误差更接近3D-MCRB;在网络连通度较小时，CWOR具有更加明显的优势.

References)

［1］ BurattiC，Conti A，DardariD，et al.An overview on wireless sensor networks technology and evolution［J］.Sensors，2009，9(9):6869－6896

［2］ Boukerche A，Oliveira H A B F，Nakamura E F，el al.Localization systems for wireless sensor networks［J］.IEEE Wireless Communications，2007，14(6):6 －12

［3］ Mao G Q，Fidan B，Anaderson B D O.Wireless sensor network localization techniques［J］.Computer Networks，2007，51(10):2529－2553

［4］ Srirangarajan S，Tewfik A H，Luo ZQ.Distributed sensor network localization using SOCP relaxation［J］.IEEE Transactions on Wireless Communications，2008，7(12):4886 －4895

［5］ Vemula M，Bugallo M E，Djuric PM.Sensor self-localization with beacon position uncertainty［J］.Signal Processing，2009，89(6):1144－1154

［6］ Lui KW K，Ma W K，So H C，et al.Semi-definite programming algorithms for sensor network node localization with uncertainties in anchor positions and/or propagation speed［J］.IEEE Transactions on Signal Processing，2009，57(2):752 －763

［7］ Wan Jiangwen，Yu Ning，Feng Renjian，et al.Localization refinement for wireless sensor networks［J］.Computer Communications，2009，32(13 －14):1515 －1524

［8］ Schwetlick H，Tiller V.Numerical methods for estimating parameters in nonlinear models with errors in the variables［J］.Te chnometrics，1985，27(1):17 － 24

［9］ Lawson C L，Hanson R J.Solving least squares problem［M］.Philadelphia:Society for Industrial and Applied Mathematics，1995

［10］ Messer H.The hybrid Cramer-Rao lower bound-from practice to theory［C］//In Proceedings of Fourth IEEE Workshop on Sensor Array and Multichannel Processing.Waltham:Signal Processing Society，2006:304 －307

(编 辑:刘登敏)

Beacon error-tolerable method for node localization in 3D w ireless sensor networks

Guo Xiaolei Yu Ning Wu Yinfeng Wan Jiangwen
(School of Instrument Science and Opto-electronics Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

For 3D wireless sensor networks(WSNs)with inaccurately positioned beacon nodes，a novel multi-hop node localizationmethod that can tolerate beacon position errorswas proposed.The influences of independent variable errors and dependent variable biases on node coordinate estimation were taken into account simultaneously.Based on the principle of constrained weighted orthogonal regression，a reliable 3Dmulti-hop localization model was constructed，and the numerical method for calculating the optimum value of node coordinates was given.The 3D multi-hop Cramér-Rao bound(3D-MCRB)for node localization under combined uncertainties in beacon positions and estimative distances was also derived.Simulation results show that the novel method is robust against beacon position errors and distance estimation errors.Inmostexperiment conditions，the multi-hop localization accuracy can be improved by at least10%.

wireless sensor networks;3D localization;beacon position error;orthogonal regression;Cramér-Rao bound

TP 393

A

1001-5965(2012)06-0810-06

2011-03-24;网络出版时间:2012-06-15 15:44

www.cnki.net/kcms/detail/11.2625.V.20120615.1544.034.htm l

国家自然科学基金资助项目(60974121，61001138)

郭晓雷(1983 －)，男，河北石家庄人，博士生，sensory@buaa.edu.cn.