评分偏差对于推荐质量的影响

胡必云 李舟军

(北京航空航天大学 软件开发环境国家重点实验室，北京 100191)

王 君

(北京航空航天大学 计算机学院，北京 100191)

巢文涵

(北京航空航天大学 北京市网络技术重点实验室，北京 100191)

评分偏差对于推荐质量的影响

胡必云 李舟军

(北京航空航天大学 软件开发环境国家重点实验室，北京 100191)

王 君

(北京航空航天大学 计算机学院，北京 100191)

巢文涵

(北京航空航天大学 北京市网络技术重点实验室，北京 100191)

从理论上分析了评分偏差对于推荐质量的影响;基于潜在偏好及已知评分对评分偏差进行度量，其中潜在偏好通过心理测量学模型计算得出;通过设定不同的评分偏差水平，对评分偏差的影响进行了实验验证.理论分析及实验验证表明:评分偏差可导致推荐准确度及覆盖度下降;基于高质量的评分数据，协同过滤算法可为用户作出好的推荐.

人工智能;信号过滤与预测;信息检索;评分偏差;数据质量;协同过滤;推荐准确度;覆盖度

个性化推荐是解决信息过载问题的行之有效的方法之一，并已广泛应用于大型的信息服务提供商，它旨在根据用户的历史偏好信息，向用户主动推荐他/她可能感兴趣的项目，如新闻、书籍等.为了提高推荐质量，研究者提出了许多推荐算法，这些算法可分为3类［1］:基于内容的推荐、协同过滤(CF，Collaborative Filtering)及混合的推荐算法.在这些算法中，CF算法得到了广泛的研究与应用.CF算法可进一步分为基于用户、基于项目及基于模型的算法，它们通常基于用户评分为用户进行推荐，其中广泛使用的数据集包括MovieLens，EachMovie，Netflix，Jester等.一般认为，评分数据稀疏会导致CF算法的推荐质量下降［2］，因此，研究者提出了很多方法以解决该问题.然而，对于评分数据的另一重要特征——数据质量问题的研究却较少，这可能是由于数据质量相对于数据稀疏更加难以衡量造成的.

在少数涉及到数据质量问题的研究中，文献［3］将推荐算法不能准确预测的评分看成是噪声数据并将它们删除，这使得推荐准确度有了一定的提高，但却造成了推荐覆盖度(coverage)下降(推荐覆盖度指算法可给出的评分预测数占待预测评分总数的比率)，后者是容易理解的，因为数据删除加剧了数据稀疏问题;文献［4］将符合随机噪声模式(CNP，Causal Noise Pattern)的用户评分系列删除，使得推荐准确度有所提高，文中未报道评分删除对推荐覆盖度的影响;文献［5］尝试了使用专家评分对普通用户进行推荐，因为专家的评分质量更高.以上文献虽然对数据质量问题进行了一定研究，并取得了一些初步的研究成果，但存在以下问题:①对数据质量问题的定义过于模糊，即将某些评分［3］或用户评分系列［4］整体地看作是噪声.然而，用户的评分可能只是在某种程度上偏离了其真实偏好，即一个评分数据可能含有噪声而不全部是噪声;②对数据质量对于CF算法推荐质量的影响机制，特别是对于推荐覆盖度的影响，没有做明确的分析与验证;③对于噪声数据的处理方式太极端，即将噪声数据整体删除，这虽然可使推荐准确度有一定的提高，但却导致推荐覆盖度下降［3］.

针对上述问题，本文首先从心理学角度对用户评分过程进行分析，并提出评分偏差的概念，以对数据质量问题进行明确的定义.同时，分析评分偏差对于CF算法每一步骤的影响，以初步研究数据质量问题对于推荐质量的影响.其次，基于心理测量学模型对评分偏差加以度量.再次，通过设定不同的评分偏差水平，进一步在现实世界数据集上验证评分偏差对于CF算法推荐质量的影响.本文最后对实验结果进行了详细分析并对未来工作进行了说明.

1 评分偏差对于CF的影响

1.1 评分偏差

CF算法常依据用户评分为用户作出推荐，而从心理学角度分析，用户根据不同项目满足他/她的潜在兴趣的程度对不同项目进行评分，因此观测到的评分只是用户潜在兴趣的一种外在表现.在评分过程中，用户可能会受到各种因素的干扰，导致用户的评分偏离于他/她的真实偏好，即产生了评分偏差.造成评分偏差的因素可以是错误地使用了评分标准，如对于一个5级评分量表来说，一个用户偏向于使用1～3的评分(可称该用户为一个较严的评分人)，那么该用户的评分2代表其真实偏好为3(2和3分别为错误的评分量表1～3和正确的评分量表1～5的中间值)，即产生了评分偏差－1(观测值2－真实值3).其它可以造成评分偏差的因素包括:对某些项目不在意而给出的随意评分、输入错误等.更为具体的例子如Jester数据集，它使用了［－10，10］的连续评分，用户通过在评分条上点击以给出评分，这种评分方式则更倾向于产生评分偏差［6］.

1.2 协同过滤(CF)

下文所提及的CF算法主要指基于用户的CF算法(user-based CF)［7］.CF 算法主要包含 3 个步骤:相似度计算、邻居选取及预测.CF算法将用户对于项目的评分看成用户评分向量，然后基于两个用户共同评分的项目(co-rated items)计算用户之间的相似度.常用的相似度计算方法有皮尔森(Pearson)相关系数、余弦相似度等［2］.在邻居选取阶段，CF算法通常选择和当前用户(需要为其作出推荐的用户)最相似的若干个用户作为他/她的邻居;然后根据邻居对于目标项目(需要为其作出评分预测的项目)的评分情况预测当前用户对于目标项目的评分;常用的预测公式如式(1)所示:

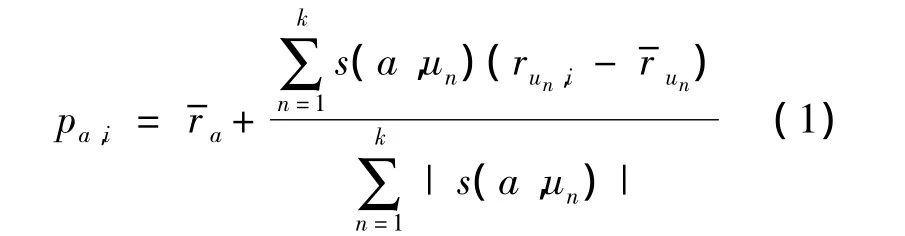
其中，pa，i是算法给出的当前用户a对于目标项目i的评分预测值;为a的平均评分;k为邻居个数;s(a，un)为 a和其邻居 un之间的相似度;run，i为un对于i的评分.值得注意的是，在邻居选取阶段选出的邻居并非全部是有效的.

定义1 有效邻居.在预测阶段实际使用到的邻居.即对于CF算法，有效用户邻居对于目标项目的评分run，i(见式(1))是存在的.

1.3 评分偏差对于CF的影响

1.3.1 评分偏差对于用户相似度计算的影响

直观地，评分偏差可导致两个具有低相似度值的用户变得更为相似，两个具有高相似度值的用户变得较不相似，即评分偏差可导致两个用户ui和uj之间的相似度值s(ui，uj)升高或降低.

例1 如表1所示，对于1～5的5级评分，其中用户u1是一个理想的评分人，她的评分ru1代表了她的真实偏好tu1，而用户u2是一个较严的评分人，他的观测评分ru2集中于评分等级1～3.如果u2正确地使用了评分等级1～5，则他的真实偏好很可能为表中第4列所列的评分tu2.根据真实偏好计算得到的u1和u2之间的Pearson相关系数是0.4，而根据观测评分计算得到的u1和u2之间的相关系数为0.2，即因为评分偏差的影响，u1和u2之间的相似程度s(u1，u2)降低;同样地，用户u3的真实偏好tu3列于表1中最后一列，但u3在评分过程中，总有值为1或－1的评分偏差，即观测到的u3的评分为表中第5列数据ru3.当使用真实偏好时，u1和u3之间的Pearson相关系数为－0.1，但是当使用观测评分时，两者的相关系数为0.1，即因为评分偏差的影响，用户u1和u3之间的相似程度s(u1，u3)升高.

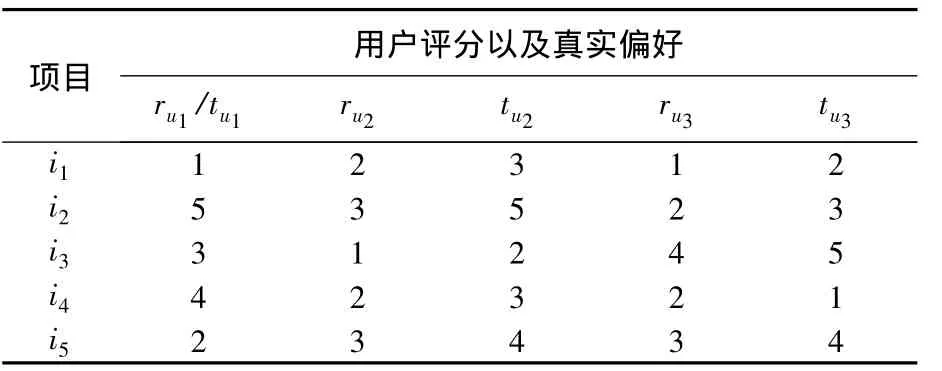
表1 用户u对于项目i的评分r及真实偏好t

1.3.2 评分偏差对于邻居选取的影响

为了便于分析，首先给出关于相似用户的假设及其推论.

假设1 两个用户共同评分的项目越多，则这两个用户倾向于越相似.

假设1是符合直觉的，即两个用户之间的共同点越多，则倾向于越相似;同时，本文依据用户评分计算得出的用户平均相似度随共评项目数变化的实验结果也反应了该假设.

基于假设1，可以得出以下推论:

推论1 两个用户之间的相似性越小，则这两个用户共同评分的项目倾向于越少.

在邻居选取阶段，评分偏差对于用户相似度计算的影响会导致具有低相似度值的用户被选择为邻居，而根据推论1，这些具有低相似度的邻居是无效邻居的可能性增大.

例2 如表2所示，由于评分偏差的影响，具有低相似度值的用户u2被选择为用户u1的邻居，CF算法目前需要为u1对于项目i4的评分进行预测(以?表示).因为u1和u2相似程度低，根据推论1，u2对于i4没有进行评分，即u2是无效邻居的可能性增大.

表2 被用户u1和u2共同评分的项目

1.3.3 评分偏差对于推荐质量的影响

具有低相似度值的邻居被使用会导致推荐准确度下降，更进一步地，由于低相似性邻居是有效邻居的可能性小，导致推荐覆盖度下降.评分偏差对于推荐质量的影响分析可总结为图1.

图1 评分偏差对于推荐质量的影响分析

2 基于心理测量学模型的偏差度量

2.1 心理测量学模型

在心理测量学研究领域，潜在特质模型(latent traitmodels)或称项目反应理论模型(item response theorymodels)，是一系列旨在通过人对项目如试题、调查问卷等的反应数据，测量人的潜在特质如能力、兴趣、满意度等的模型［8］.典型的项目反应理论模型有Rasch模型，如式(2)所示.Rasch模型最初用于教育测量学领域，随着模型及其参数估计技术的发展，Rasch模型被用于越来越多的心理测量领域［9］.

在不同的应用领域中，Rasch模型的参数意义是不同的.在传统的教育测量领域，式(2)建模了学生u答对题目i的概率p(ru，i=1)与学生能力θu及题目难度bi之间的关系［8］;因为本文主要考虑通过用户对于项目的评分数据测量用户潜在兴趣，所以将p(ru，i=1)解释为用户u对于项目i的反应为积极(如表示感兴趣或评分为1)的概率;将θu解释为用户的潜在兴趣(latent interest);将bi解释为项目的可接受程度(agreeability).因此，式(2)直观上表示了用户的潜在兴趣越强，则越可能表现出积极的反应.

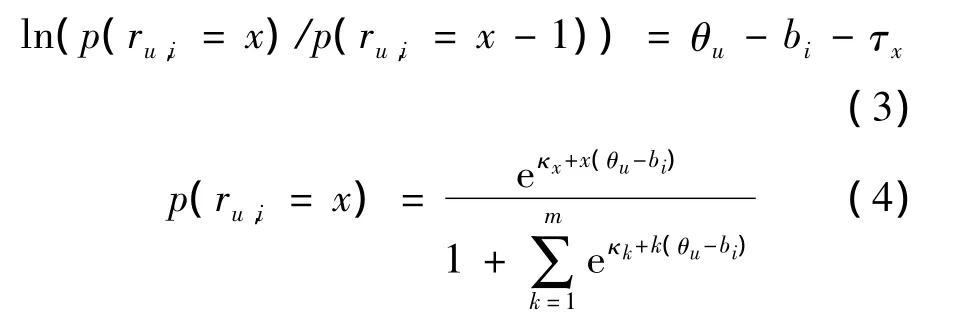
2.2 心理测量学模型与个性化推荐

文献［11］将心理测量学模型引入个性化推荐算法的研究中，并提出了基于潜在兴趣的CF算法，实验结果表明基于潜在兴趣的CF算法相比于传统CF算法可提高推荐准确度.

上述研究结果表明，将心理测量学引入个性化推荐算法研究中是有益的.提出具有更高推荐准确度的算法虽然重要，但对于评分数据质量问题的研究同样重要，因为低质量的数据可能会造成研究结果产生偏差甚至误导.因此，鉴于用户在评分过程中倾向于产生评分偏差，前期工作［12］提出了使用潜在偏好(latent preference)表示用户偏好，其中潜在偏好通过心理测量学模型计算得出，并实验验证了潜在偏好相比于观测评分可更准确地表示用户偏好.然而，文中并没有对评分偏差对于推荐质量的影响进行实验分析.本文在前期研究的基础上，提出评分偏差的度量方法，并分析评分偏差对于推荐质量的影响，从而对推荐算法作出更为客观的评价.

2.3 评分偏差度量

具体地，评分偏差的度量分为3个步骤:

1)依据用户评分及心理测量学模型估计用户潜在兴趣θu.本文用Rasch模型参数估计软件Winsteps［13］.Winsteps 首先将 θu，bi及 τx初始化为0，然后遍历用户评分数据集，通过正态逼近算法(PROX，Normal Approximation Estimation Algorithm)迭代更新θu及bi，直至θu及bi的变化程度小于某一阈值(详细的推导过程可参见文献［14］).Winsteps然后通过 JML进行第2阶段的参数估计.首先依据当前 θu，bi，τx值及 Rasch 模型计算用户评分期望值，然后依据评分期望值与评分的差别程度，通过 Newton-Raphson算法对θu，bi及τx进行迭代更新.例如，如果依据目前参数计算得到的用户期望评分总分小于实际总分，则提高用户的潜在兴趣值θu.具体的参数迭代更新公式可参见W right等的推导［15］.

2)对于每一用户评分，依据用户潜在兴趣，计算相应的潜在偏好，如式(5)，其中 lu，i为计算得到的用户u对于项目i的潜在偏好:

3)依据潜在偏好，计算用户的评分偏差R.计算公式见式(6)，其中ru，i为用户u对于项目i的评分.前期工作表明，潜在偏好lu，i相比于观测评分 ru，i可更准确地表示用户偏好［12］，因此，由式(6)度量用户评分偏差是可行的.

3 实验验证

3.1 数 据 集

实验采用了广泛使用的数据集之一MovieLens［2］.该数据集含有943个用户对于1 682个电影项目的100000个评分.评分可取值为1～5.实验随机选取了80%的用户评分作为训练集，其余的评分作为测试集.

3.2 推荐质量度量标准

实验采用广泛使用的平均绝对误差(MAE，Mean Absolute Error)［2］作为推荐准确度的度量标准，用E表示:

其中，pu，i为算法给出的用户u对于项目i的评分预测值;ru，i为测试集中的对应评分.MAE值越小，则推荐准确度越高;推荐覆盖度(coverage)定义为算法可给出的预测值数目占测试评分总数N的比例［5］.

3.3 实验过程及结果分析

实验首先通过训练集数据使用Rasch模型参数估计软件Winsteps［13］估计用户潜在兴趣;然后针对训练集中的每一用户评分ru，i，计算其对应的潜在偏好 lu，i及评分偏差 Ru，i=ru，i－ lu，i，接着，通过设定不同的评分偏差水平a(a分别取值0，0.2，0.4，…，1.0)形成不同的训练数据集 tu，i=aRu，i+lu，i.通过由不同评分偏差水平形成的训练集，分别分析评分偏差对于用户相似度计算、邻居选取及推荐质量的影响.

实验采用Pearson相关系数［2］计算用户相似度，邻居数 k分别设置为 5，10，…，60，评分预测公式为式(1).

3.3.1 评分偏差对于相似度计算的影响实验分析

实验计算了在不同评分偏差水平a下，含有不同共评项目数c＞x(x分别取值为2，4，…，10，15，25，…，105)的用户之间的平均相似度，结果如图2所示(为了清楚的呈现实验结果，本文省略了某些参数取值下的结果，或将不同参数下的结果分别呈现).

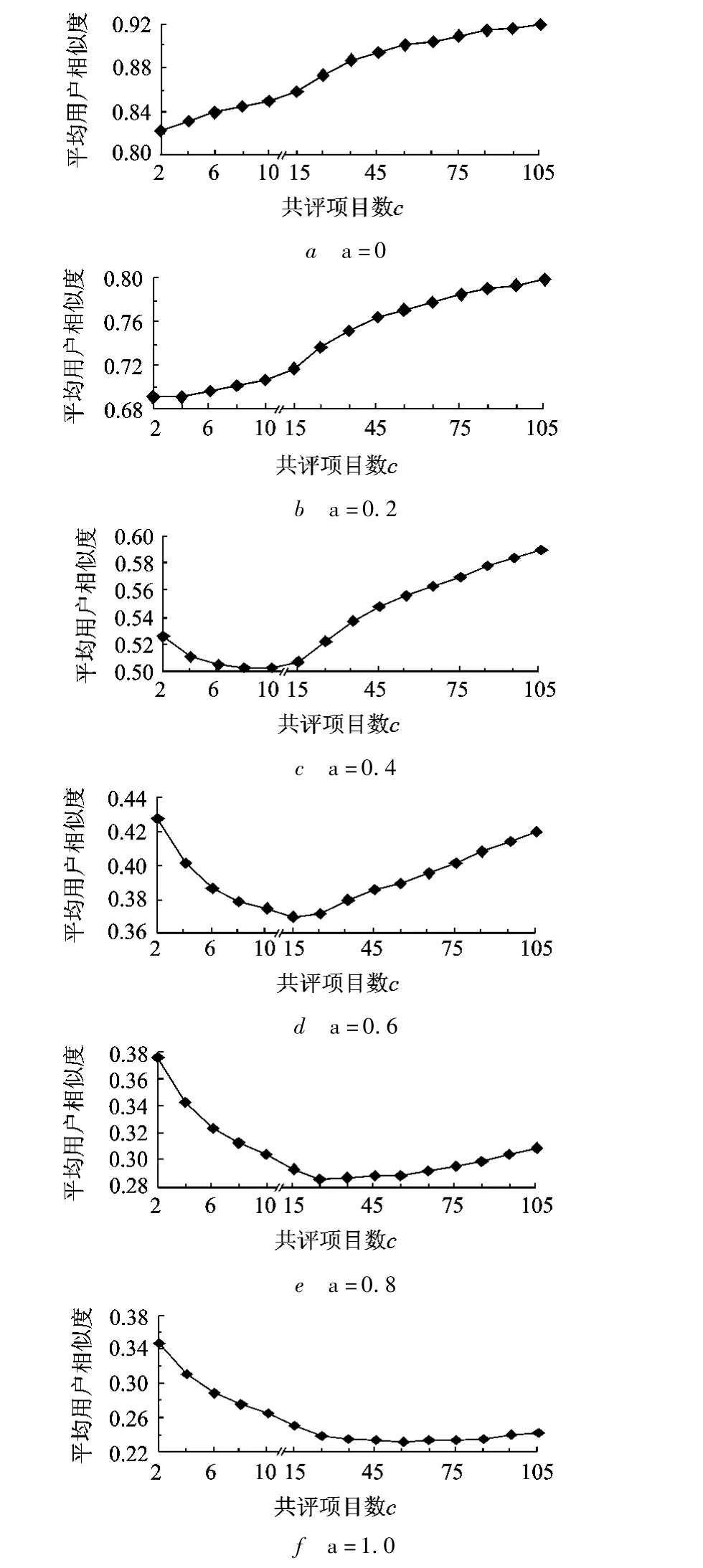
图2 平均用户相似度随共评项目数c的变化情况

图2的结果显示，随着偏差水平的增大，具有低相似度的用户之间的相似水平相对提高;具有高相似度的用户之间的相似水平相对降低.例如，对于a=0.2，c＜10的这些低相似性用户(图2b)，随着偏差水平的升高，这些用户之间的相似度值逐渐相对提高(相对于同一偏差水平下，c＞10的那些用户);而对于a=0.2，c＞10的这些高相似性用户，随着偏差水平的升高，这些用户之间的相似度值逐渐相对下降.这些相似度变化与本文第1.3.1节的分析结果一致(图1中A→B).

3.3.2 评分偏差对于邻居选取的影响实验分析

图2的结果显示，随着偏差水平的升高，具有低相似度值的用户在邻居中占的比率增大(图1中 B→C).例如，对于 a=0.2，c＜10 的这些低相似性用户(图2b)，当偏差水平升至0.8及1.0时，CF算法完全优先选择这些用户作为邻居，而这些用户之间的共评项目数相对较少，即是有效邻居的可能性小.

为了进一步分析邻居的有效性，定义平均有效邻居比(average effective neighbor ratio)，用e表示，如式(8)，其中N为测试集中的评分个数，ni1为预测任一测试集中的评分时，有效邻居的个数，ni2为可选邻居的个数.

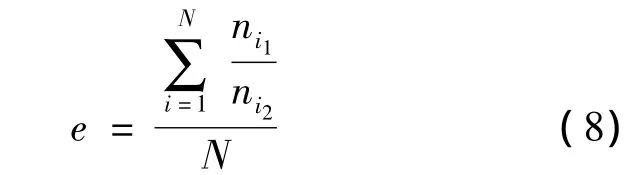
当邻居数k设为不同值时，平均有效邻居比的实验结果报告于图3.图3显示，随着偏差水平的升高，邻居的有效性降低;而前述分析表明:偏差水平增大，邻居中低相似度值的用户比率增大;据此两点可得出结论:具有低相似度值的用户邻居的有效性低(图1:C→E).

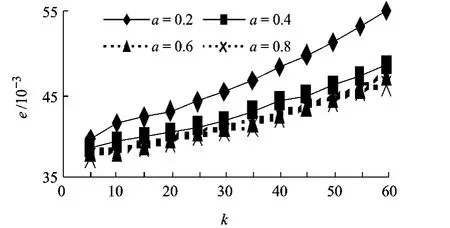
图3 不同评分偏差水平a下的平均邻居有效比

3.3.3 评分偏差对于推荐质量影响实验分析

图4显示了不同偏差水平下的推荐准确度结果，可见，平均绝对误差随偏差水平a的增加而增加，即随着偏差水平的提高，推荐准确度下降.最大降幅达20%(当邻居数k为5时，将偏差水平平均绝对误差从0.2提高至0.8，a值从 0.785 增至0.945).

不同偏差水平下的推荐覆盖度结果见图5，可见，推荐覆盖度随偏差水平a的增加而下降，即随着偏差水平的提高，推荐覆盖度下降.最大降幅达12%(当邻居数k=60时，将偏差水平a从0.2提高至0.8，推荐覆盖度从 0.648 降至 0.572).

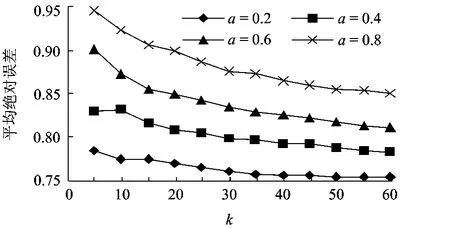
图4 不同评分偏差水平a下的推荐准确度

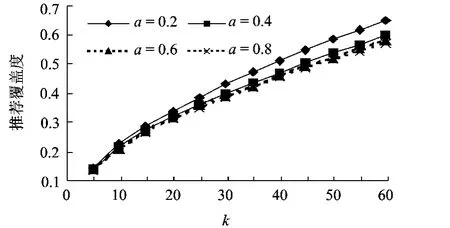
图5 不同评分偏差水平a下的推荐覆盖度

推荐准确度主要与用户相似度值有关，即所选邻居是否具有真实可靠的高相似性;推荐覆盖度主要与邻居有效性有关，即针对每一测试评分，是否可找到有效的用户邻居.因此，在实验分析了评分偏差对于用户相似度计算及邻居选取的影响后，不难得出评分偏差对于推荐准确度及覆盖度的影响，即评分偏差使得相似度值低的用户被选择为邻居，导致推荐准确度下降(图1中A→B→C→D);同时，相似度值低的邻居的有效性低，导致推荐覆盖度下降(图1中A→B→C→E→F).

4 结论

本文的主要贡献在于:①给出了评分数据质量问题的明确定义，即评分偏差;②对评分偏差对于推荐质量(包括推荐准确度及覆盖度)的影响机制进行了分析，并基于心理测量学模型对用户评分偏差进行了度量，通过实验验证了评分偏差的影响:评分偏差导致具有低相似度值的用户被选择为邻居，从而导致推荐准确度下降;同时，由于具有低相似度值的邻居的有效性低，导致推荐覆盖度下降;③结果表明，基于高质量的数据，CF算法可获得好的推荐准确度及覆盖度.

References)

［1］ Gediminas A，Alexander T.Toward the next generation of recommender systems:a survey of the state-of-the-art and possible extensions［J］.IEEE Trans on Knowledge and Data Engineering(TKDE)，2005，17(6):734 －749

［2］ Badrul S，George K，Joseph K，et al.Item-based collaborative filtering recommendation algorithms［C］//Proc of10th International World Wide Web Conference(WWW'01).New York:ACM Press，2001:285 －295

［3］ O'Mahony M P，Hurley N J，Silvestre G CM.Detecting noise in recommender system databases［C］//Proc of the 10th International Conference on Intelligent User Interfaces(IUI'06).New York:ACM Press，2006:109 －115

［4］ Cao Huanhuan，Chen Enhong，Yang Jie，et al.Enhancing recommender systems under volatile user interest drifts［C］//Proc of the 18th ACM Conference on Information and Knowledge Management(CIKM'09).New York:ACM Press，2009:1257 －1266

［5］ Xavier A，Neal L，Pujol JM，et al.The wisdom of the few:a collaborative filtering approach based on expert opinions from the web［C］//Proc of the 32nd International ACM SIGIR Conference on Research and Development in Information Retrieval(SIGIR'09).New York:ACM Press，2009:532 －539

［6］ Herlocker JL，Konstan JA，Terveen L G，et al.Evaluating collaborative filtering recommender systems［J］.Transactions on Information Systems(TOIS)，2004，22(1):5 －53

［7］ Wang Jun，de Vries A P，Reinders M J T.Unifying user-based and item-based collaborative filtering approaches by similarity fusion［C］//Proc of the29th International ACM SIGIRConference on Research and Development in Information Retrieval(SIGIR'06).New York:ACM Press，2006:501 －508

［8］杜文久.高等项目反应理论［M］.重庆:西南师范大学出版社，2007:71－88 Du Wenjiu.Advanced item response theory［M］.Chongqing:Southwest Normal University Press，2007:71 －88(in Chinese)

［9］ Cheng Yunghsiang.Exploring passenger anxiety associated with train travel［J］.Transportation，2010，37(6):875 －896

［10］ David Andrich.A rating formulation for ordered response categories［J］.Psychometrikia，1978，43(4):561 － 573

［11］ HuBiyun，Li Zhoujun，Wang Jun.User's latent interest-based collaborative filtering［C］//Proc 32nd European Conference on Information Retrieval(ECIR'10).Berlin:Springer-Verlag，2010:619－622

［12］ HuBiyun，Li Zhoujun，Chao Wenhan，et al.User preference representation based on psychometric models［C］//Proc 22nd Australia Database Conference(ADC'11).Sydney:ACS，2011:57－64

［13］ LinacreMike.WINSTEPS Rasch measurement computer program［EB/OL］.Chicago:Winsteps.com，2007［2011-05-15］.http://www.winsteps.com

［14］ Linacre Mike.PROX for polytomous data［J］.Rasch Measurement Transactions，1995，8(4):400

［15］ Wright B D，Masters G N.Rating scale analysis［M］.Chicago:MESA Press，1982:100

(编 辑:文丽芳)

Effect of rating residual on recommendation quality

Hu Biyun Li Zhoujun

(State Key Laboratory of Software Development Environment，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

Wang Jun

(School of Computer Science and Technology，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

Chao Wenhan

(Key Laboratory of Network Technology of Beijing，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

The effect of the rating residual on recommendation quality was analyzed.The rating residual was measured through user ratings and latent preferences.Latent preferences were computed with psychometric models.With different levels of rating residual，the effect of the rating residual was experimentally evaluated on real world datasets.Theoretical analysis and experimental results show that rating residual has negative effects on recommendation accuracy and coverage.Based on high quality of data，collaborative filtering algorithms can make precise recommendations for users.

artificial intelligence;signal filtering and prediction;information retrieval;rating residual;data quality;collaborative filtering;recommendation accuracy;coverage

TP 182

A

1001-5965(2012)06-0823-06

2011-03-18;网络出版时间:2012-06-15 15:43

www.cnki.net/kcms/detail/11.2625.V.20120615.1543.024.htm l

国家自然科学基金资助项目(61170189，60973105);软件开发环境国家重点实验室自主研究课题资助项目(SKLSDE-2011ZX-03)

胡必云(1982 －)，女，安徽六安人，博士生，hubiyun@cse.buaa.edu.cn.