协同无线通信系统中的分布式自适应功率分配

李国彦 张有光

(北京航空航天大学 电子信息工程学院，北京 100191)

协同无线通信系统中的分布式自适应功率分配

李国彦 张有光

(北京航空航天大学 电子信息工程学院，北京 100191)

在系统总功率一定的情况下，通过在协同节点间进行优化的功率分配以改善系统的接收性能.针对单中继协同传输，推导了节点间最优功率分配因子的闭式表达式，给出了中继节点的激活条件，仅当信道的衰落特性满足该条件时，中继节点才发送信号到目的节点，否则进入空闲状态.多节点协同传输场景下，直接根据系统的输出信噪比难以得到节点间最优功率分配因子的闭式表达式.因此，推导了系统输出信噪比的上界，在此基础上，提出了一种新的功率分配方法.将整个功率分配过程分成两步，采用迭代的方法实现节点间的最优功率分配.仿真结果表明，对于单中继节点的情况，所提出的功率分配方案能够获得约1～2 dB的性能增益，随着参与协同传输的节点数的增大，迭代的功率分配可使系统获得显著的性能提升.

无线网络;协同传输;自适应;功率分配

协同通信［1－5］通过终端间的相互协作可引入空间分集优势，能够克服衰落，提高通信质量.实际的协同无线网络中，由于距离、地形等因素的影响，节点间具有不同的信道状态.这意味着在源节点和协同节点分配不同的功率往往导致迥然不同的通信性能.然而，由于节点的移动，节点间的信道状态往往随着节点间相对位置的改变而随机变化，因此功率分配算法需要对信道状态的变化具有自适应能力.同时，优化的功率分配能够减小节点能耗，有效延长节点寿命.文献［6］提出一种近似最优的功率分配方法，能够在功率约束下实现中断概率最小化.文献［7］针对多跳协同传输提出了一种最小化最大功率分配方案，以实现网络存活时间最大化.文献［8］从能量角度出发，给出了一种最小化能量消耗的功率分配策略.然而，上述的功率分配方案均属于固定的功率分配，不能根据节点间信道特性的变化动态调整节点的发射功率.本文在单个中继节点和多个中继节点与源节点协同传输的场景下，以系统的输出信噪比为衡量标准，对协同节点间的自适应最优功率分配进行了研究，给出了相应的功率分配方法并进行了性能仿真.

1 单中继协同传输

如图1所示，系统由1个源节点(S)，1个目的节点(D)和1个中继节点(R)构成.节点X∈{S，R}与节点 Y∈{R，D}(X≠Y)之间的信道衰落系数表示为hXY=βXY/d2XY，包含路径损耗以及瑞利衰落带来的影响，其中βXY为服从瑞利分布的随机变量，dXY表示节点X和Y之间的距离，hXY的方差为σ2

XY.中继节点R受到半双工的约束，源节点和中继节点采用正交的信道传输信息，这里采用时分的方式.第一个阶段，源节点S发送信息，中继节点R和目的节点D接收信息;第二个阶段，中继节点R将接收到的信号经放大处理后发送到目的节点，目的节点将接收到的两个阶段的信号进行合并后检测.

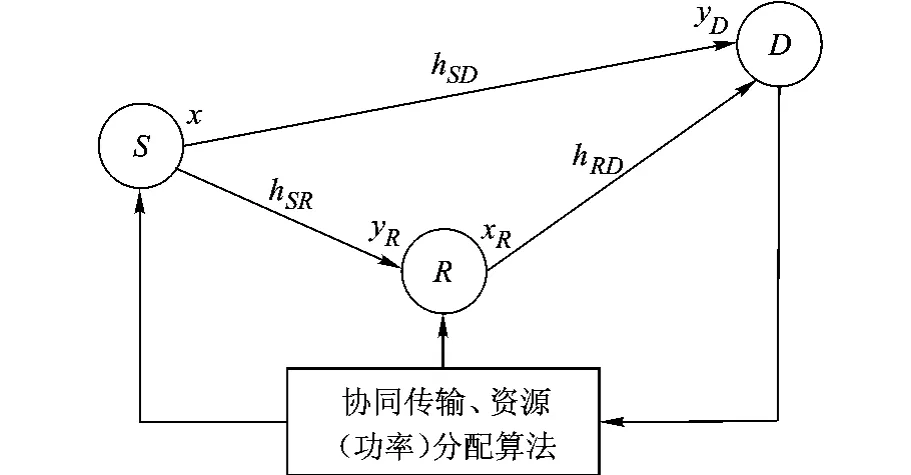
图1 协同传输系统模型

假设系统的总功率为P，源节点和中继节点的发射功率分别为PS=ζP，PR=(1－ζ)P，其中，ζ∈(0，1］，(1 － ζ)∈［0，1)分别表示源节点和中继节点的功率分配因子.在第一个阶段，中继节点和目的节点的接收信号可以表示为

其中，nR和nD，1分别是中继节点R和目的节点D处的零均值，方差为σ2的复高斯噪声随机变量.中继节点在接收到源节点的信号后，将其进行放大后发送，因此，中继节点的发送信号为

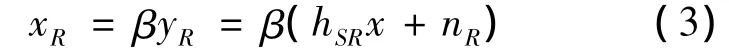
其中，β为中继节点处的放大因子，满足下式所示的功率约束条件

由式(4)可得放大因子β为

在高信噪比的情况下，式(5)所示的放大因子可以表示为

第二个阶段，中继节点R发送信号xR到目的节点，此时，目的节点的接收信号为

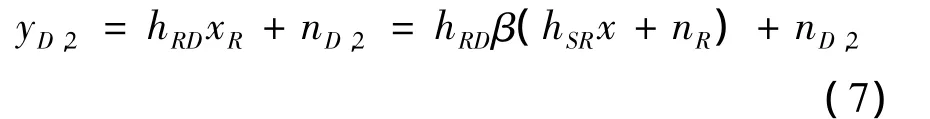
这里，nD，2是目的节点D处的零均值复高斯噪声随机变量，不失一般性，假设各噪声 nR，nD，1，nD，2相互独立且具有相同的方差σ2=1.

因此，目的节点获得了两个关于发送信号x的信息，将其写为如下的矩阵表示形式

由式(7)可以看出，中继节点R在放大有效信号的同时也放大了噪声，这将导致目的节点D在两个阶段接收信号中的噪声具有不同的方差，而MRC(Maximum-Ratio-Combining)仅在合并的各路信号具有相同的噪声方差时才能获得最优性能［9］.因此，在进行MRC之前，首先要进行噪声的白化处理.此时，系统的输出信噪比可以表示为

对于一个通信系统，其误比特率可以描述为系统输出信噪比的单调递减函数，最大化系统的输出信噪比等价于最小化误比特率.因此，这里的最优化问题可以描述为

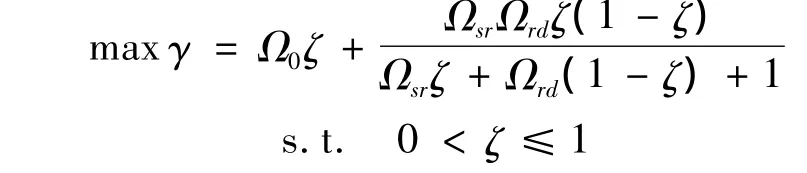
令Ω =Ω0(Ωsr－Ωrd)－ΩsrΩrd，则式(10)可写为

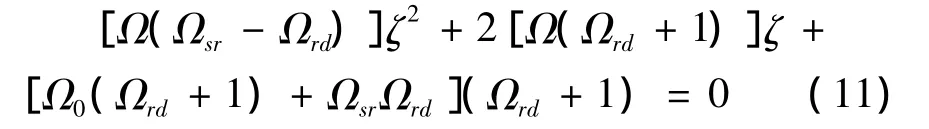
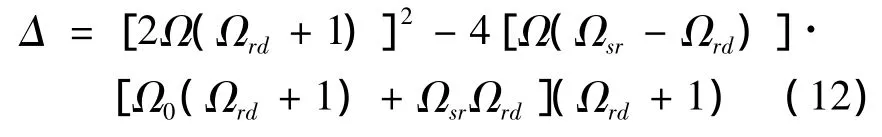
1)当Δ＜0时，对式(12)化简后得到Ω＞0.即，当Ω＞0时，式(11)无实数解，这意味着函数f(ζ)在 ζ∈(0，1］不存在导数为零的点，即 f(ζ)在ζ∈(0，1］为单调函数;而当 ζ=0，ζ=1 时，分别有f(0)=0，f(1)=Ω0＞0，所以，函数 f(ζ)在 ζ∈(0，1］为单调增加函数.因此，在ζ=1时f(ζ)取得最大值，即系统获得最大的输出信噪比.此时，源节点使用全部的功率发送，而中继节点则处于空闲状态，系统的最大输出信噪比为

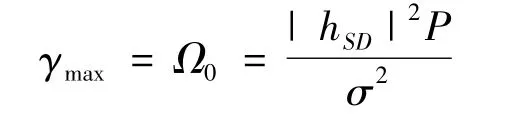
2)当Δ＞0时，有Ω＜0.此时，式(11)有两个不同的实数解:

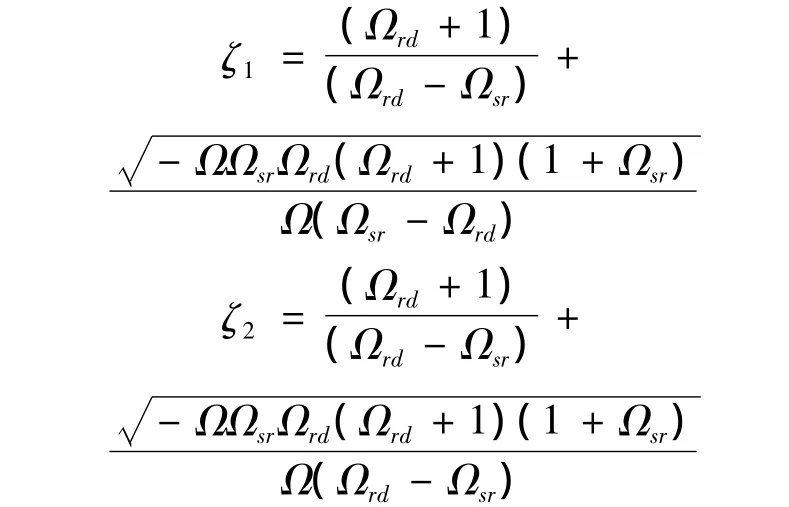
容易判断，ζ1＜0 或 ζ1＞1，不满足 ζ∈(0，1］的条件.因此，只有 ζ2是(0，1］上可能的解.

①当0＜ζ2＜1时，源节点的发射功率为PS=ζ2P，中继节点的发射功率为PR=(1－ζ2)P.将ζ2代入式(9)中，可得系统的最大输出信噪比

② 当 ζ2≥1 或 ζ2≤0 时，f(ζ)在 ζ∈(0，1］为单调增函数，因此，f(ζ)在ζ=1取得最大值.此时，源节点的发送功率为PS=P，中继节点的发送功率PR=0，即中继节点不参与数据发送.系统的最大输出信噪比为

3)当Δ=0时，有Ω=0.式(11)有两个相同的实数解:

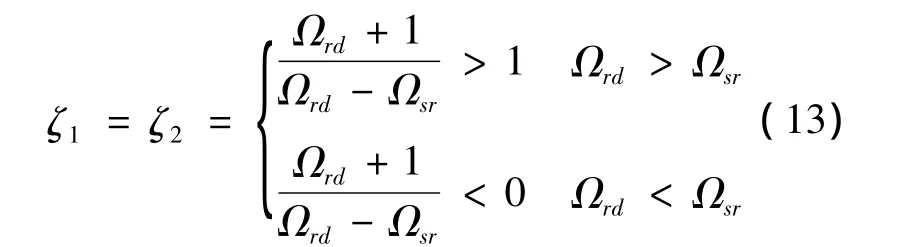
根据式(13)可知，f(ζ)在ζ=1取得最大值.因此，系统的最大输出信噪比为

认知负荷理论(Cognitive Load Theory)是由澳大利亚教育心理学家John Sweller等人于20世纪80年代末90年代初提出,[9-11]认为人的认知资源(工作记忆)容量是有限的，主张在学习过程中内在认知负荷、外在认知负荷和相关认知负荷的总量应该限制在工作记忆容量的范围之内，否则学习就会受到阻碍，甚至无法继续进行下去.

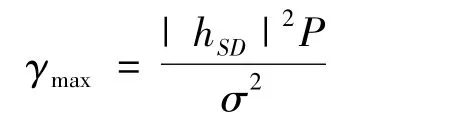
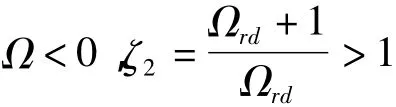
根据以上分析可以看出，仅在Ω＜0且0＜ζ2＜1时，中继节点才处于激活状态，参与数据发送，而在其它情况下，中继节点将进入空闲状态，此时最优的传输为从源节点到目的节点的直接传输.因此，根据条件

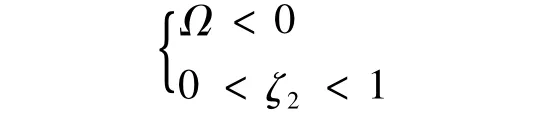
可以得到下面的中继节点激活条件:

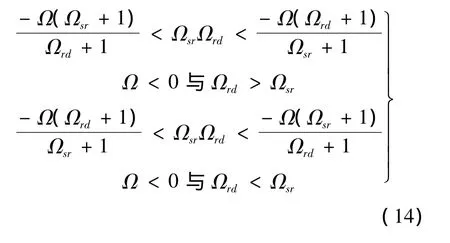
综合上述分析，可得协同节点间的最优功率分配因子为

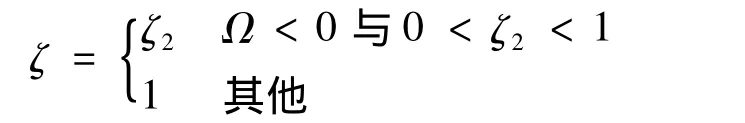
在高信噪比的情况下，有如下的最优化问题:

采用类似的分析方法，可以得到这种情况下的中继节点激活条件:

此时，最优的功率分配因子为

式(14)表明只有当信道特性满足该条件时，中继节点才参与数据发送，否则进入空闲状态.

2 多节点协同传输

在多个节点参与协同传输的情况下，源节点的信号可以经多个中继节点传输到目的节点.假设参与协同传输的节点数为M+1，源节点和各中继节点的发射功率为

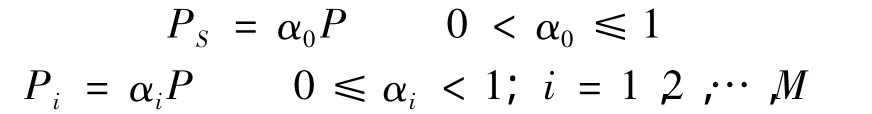
在式(5)中令 PR=Pi，hSR=hSRi就得到了节点Ri的放大因子

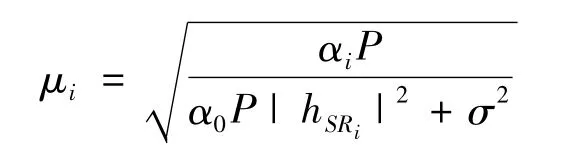
其中，hSRi表示源节点S到中继节点Ri的信道系数.此外，中继节点Ri到目的节点的信道系数表示为hRiD.目的节点采用MRC接收信号，此时，系统的输出信噪比可以表示为

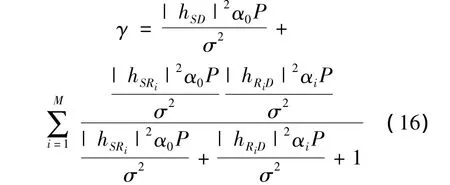
这种情况下，基于式(16)得到功率分配因子的闭式解比较困难［10］.因此，这里通过分析式(16)的上界，分析其渐进的功率分配.

在高信噪比的情况下，式(16)所示的信噪比可以表示为

不失一般性，假设各节点的噪声方差σ2=1，则上式可以写成

下面求解式(17)的最优化问题，采用拉格朗日乘子法，可以得到下面的条件函数:

根据条件极值的定义，可以得到下面的方程组:

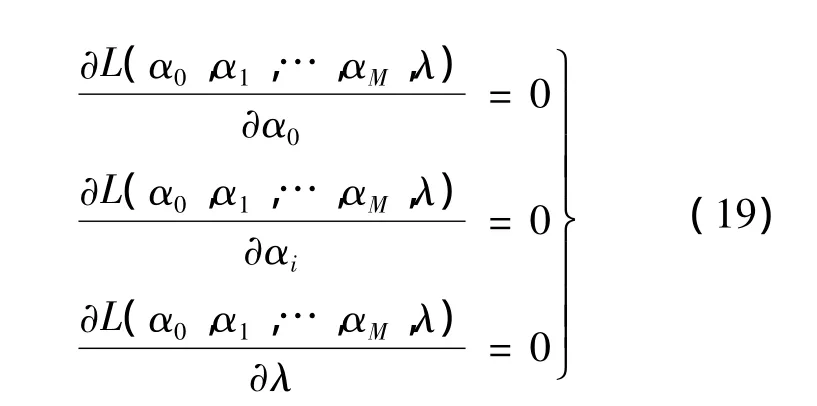
由式(19)可以看出，该方程组包含了M+2个未知数，要得到功率分配解，需要求解M+2个方程，在计算过程中需要求解的系数随中继节点数的增加而增加，且计算的复杂度随中继节点的增加迅速提高.基于此，可以采用迭代算法进行求解.

迭代算法是在上面分析的基础上，将整个功率分配过程分为两步，即首先给定源节点的功率(功率分配系数α0)，再将剩余的功率在中继节点间进行最优的分配，根据得到的功率分配结果计算系统的输出信噪比，最后根据信噪比结果调整功率分配系数，直到系统能够获得最大的输出信噪比.需要说明的是，较多的研究已经表明α0位于0.5附近，因此，在迭代计算过程中可以将α0的初值设定为0.3，这样不但不会影响求解结果，而且能够减少迭代次数，节约时间.

在给定源节点的功率后，式(19)所示的方程组可以写成

由式(20)可得

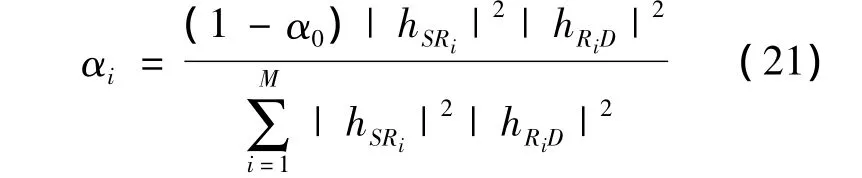
由式(21)可以看出，各中继节点的功率分配与直接链路(S-D)的传输特性无关，且当α0≠1时，有αi≠0，即，各中继节点都参与传输.迭代法的算法流程如图2所示.

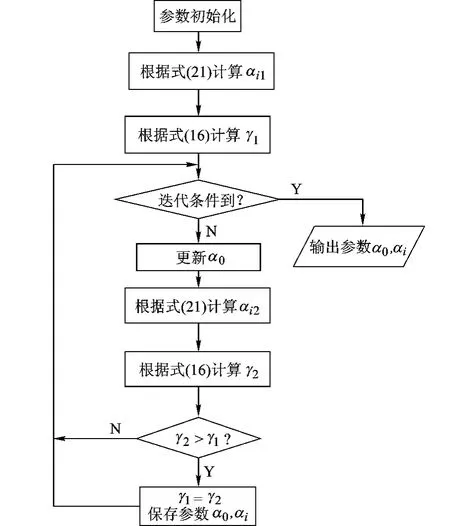
图2 迭代算法实现流程

实际的无线系统中，接收端在完成功率分配因子的计算后，可以通过一个反向信道将其发送到源节点和中继节点，源节点和中继节点根据接收到的功率分配信息调整自身的发射功率.

3 仿真结果与分析

为了验证所提出的功率分配方案的性能，本节对其进行了仿真.仿真中，源节点和目的节点之间的距离为1，坐标分别为(0，0)和(1，0)，中继节点在横坐标x为0～1，纵坐标 y为 －0.5～0.5的范围内移动，信号的调制方式为BPSK(Binary Phase Shilft Keying).对于单中继节点的场景，从以下几种情形将其与直接传输、等功率分配的固定 AF(Amplify-and-Forward)，DF(Decode-and-Forward)协同传输进行了性能对比.

种方案的误比特率(BER，Bit Error Rate)性能.由图可以看出，低信噪比时，DF的性能相比直接传输略差，但随着信噪比的提高，其性能将逐渐好于直接传输.同时，与其它方案相比，自适应的功率分配能够获得最好性能.在BER为10－4时，与等功率分配的AF传输相比，自适应的功率分配能够获得约1.3 dB的性能增益.

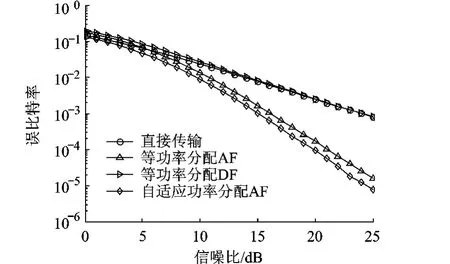
图3 时的BER性能

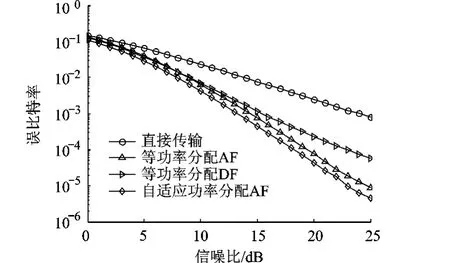
图4 时的BER性能

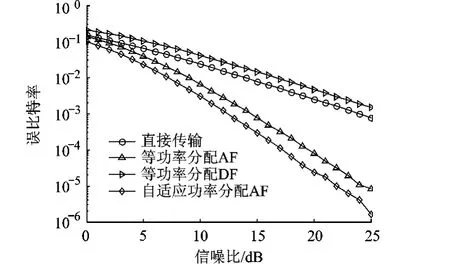
图5 时的BER性能

图6 时的BER性能

从图3～图6可以看出，在如图1所示的协同传输网络中，所提出的自适应功率分配方案能够获得约1～2 dB的性能增益，同时，该增益与中继节点相对源节点和目的节点的位置有关.

针对多节点协同传输的场景，分别在对称信道和非对称信道下对迭代的功率分配方法进行了性能仿真.图7给出的是在中继节点数 M=3，对称信道()下采用迭代功率分配算法的BER性能.由图可见，与其它方案相比，迭代的功率分配获得了最优性能，在BER为10－5时，与等功率分配的AF传输相比，采用迭代的功率分配能够获得约2 dB的性能增益.

由图7、图8可以看出，无论是在对称或非对称信道下，采用迭代的功率分配都能够显著提升系统性能.

图7 对称信道=2.9(i=1，2，3)下，迭代算法的BER性能

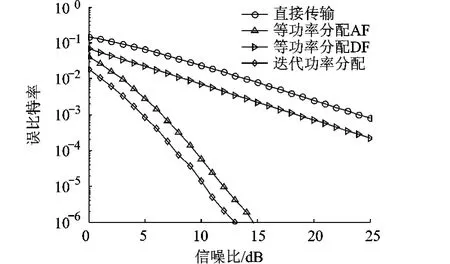
图8 非对称信道}下，迭代算法的BER性能

4 结论

协同传输系统中，由于节点的移动，节点间的信道状态随之变化，所以根据信道特性为源节点和中继节点分配不同的发射功率通常会导致迥然不同的传输性能.单中继节点的情况下，采用自适应的功率分配能够使系统获得约1～2 dB的性能增益，同时，该增益与中继节点相对源节点和目的节点的位置有关.多节点协同传输的情况下，基于系统输出信噪比上界的迭代功率分配方法能够使系统获得约2 dB的性能增益.

References)

［1］ Vardhe K，Reynolds D，Woerner B D.Joint power allocation and relay selection for multiuser cooperative communication［J］.IEEE Transactions on Wireless Communications，2010，9(4):1255－1260

［2］ Ikki SS，Ahmed M H.Performance analysis of adaptive decodeand-forward cooperative diversity networks with best-relay selection［J］.IEEE Transactions on Communications，2010，58(1):68－72

［3］ Badia L，Levorato M，Librino F，et al.Cooperation techniques for wireless systems from a networking perspective［J］.IEEE Wireless Communications，2010，17(2):89 － 96

［4］ Li Jiangyuan，Petropulu A P，Poor H V.Cooperative transmission for relay networks based on second-order statistics of channel state information［J］.IEEE Transactions on Signal Processing，2011，59(3):1280 －1291

［5］ Shi Jin，McKay M R，Zhong Caijun，et al.Ergodic capacity analysis of amplify-and-forward MIMO dual-hop systems［J］.IEEE Transactions on Information Thory，2010，56(5):2204 －2224

［6］ Tsai Yuh-Ren，Lin Li-Cheng.Optimal power allocation for decode-and-forward cooperative diversity under an outage performance constraint［J］.IEEE Communications Letters，2010，14(10):945－947

［7］ Savazzi S，Spagnolini U.Energy aware power allocation strategies formultihop-cooperative transmission schemes［J］.IEEE Journal on Selected Areas in Communications，2007，25(2):318 －327

［8］ Mahinthan V，Lin Cai，Mark JW，et al.Partner selection based on optimal power allocation in cooperative-diversity systems［J］.IEEE Transactions on Vehicular Technology，2008，57(1):511－520

［9］ Goldsmith A.Wireless communications［M］.Cambridge，UK:Cambridge University Press，2005

［10］ Annavajjala R，Cosman P C，Milstein L B.Statistical channel knowledge-based optimum power allocation for relaying protocolsin the high SNR regime［J］.IEEE Journal on Selected Areas in Communications，2007，25(2):292 － 305

(编 辑:娄 嘉)

Distributed adaptive power allocation in cooperative wireless communication systems

Li Guoyan Zhang Youguang

(School of Electronics and Information Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

The performance of the cooperative transmission system can be improved significantly by allocating powers optimally among cooperative nodes when the system has a total power constraint.For a two-hop cooperative transmission system with only one relay node，the closed-form expression of the optimal power allocation factor was derived and a relay activation condition was acquired.If and only if the fading characteristics of the channels satisfy this condition，the relay transmits signals to the destination;otherwise，it will stay in the idle state.For a system with more than one relay node，the closed-form power allocation factors are difficult to derive directly based on the output signal-to-noise ratio(SNR)of the system.So，an SNR upper bound was derived and a novel power allocation scheme was proposed.The whole power allocation was divided into two stages and the optimal power allocation was implemented by using an iterative algorithm.Simulation results show that for a system with only one relay node，the proposed power allocation scheme can yield about1～2dB performance gains compared to the equal power allocation，as the number of relays increase，the performance of the system improved greatly when using the iterative power allocation method.

wireless networks;cooperative transmission;adaptive;power allocation

TN 925

A

1001-5965(2012)06-0793-06

2011-03-21;网络出版时间:2012-06-15 15:44

www.cnki.net/kcms/detail/11.2625.V.20120615.1544.033.htm l

国家973计划资助项目(2010CB731803)

李国彦(1981 －)，男，河北石家庄人，博士生，lgy198211@ee.buaa.edu.cn.