Amplitude方程的分歧分析*

李 源，方晓超，张俊超

(1.哈尔滨师范大学;2.哈尔滨学院)

0 引言

分歧现象是半线性偏微分方程研究领域当中一类非常重要的非线性现象，它的研究可以追溯到十八世纪以来对流体力学，非线性震动等一些现象的研究.至今，在动力系统，非线性分析等研究和计算机辅助的推动下，分歧理论得到了广泛的应用，尤其是在生态学方面的应用，使得分歧理论具有强烈的实际背景.

在带守恒量系统的模式生成的研究中，Amplitude方程起着重要的作用，有时在自然科学的许多领域寻找模式生成最后归结于Amplitude方程的研究［1］.在该文中考虑了偏微分方程组

在圆柱形区域(0，L)×R+关于边值条件ux=vx=0在x=0，L处的解.这里有两个参数σ与μ，其中σ＞0，μ∈R.

2001年，Cox和 Matthews［2］首先提出了Amplitude方程(1).文献［3］中研究了方程(1)的奇异周期模式解的存在性与稳定性，对于其稳态方程，通过加强周期性与一致性条件构造了三类简单的集中周期模式.

该文将用文献［4］中的局部分歧定理研究方程(1)的分歧现象.

定理1［4］设F:R×X→Y是连续可微的，假设对所有λ∈R F(λ，u0)=0，在(λ0，u0)，F满足

且N(Fu(λ0，u0))=span{w0} (F1)混合导数Fλu存在并连续，且满足

则方程F(λ，u)=0在(λ0，u0)附近的解由u= u0及(λ(s)，u(s))组成，其中s∈I=(－δ，δ)，且(λ(s)，u(s))为连续函数满足λ(0)=λ0，u(s)=u0+sw0+o(s).如果F∈C2，则(λ(s)，u(s))连续可微且

其中l∈Y*满足N(l)=R(Fu(λ0，u0))⊥.如果还满足

则λ'(0)≠0，跨越式分歧在点(λ0，u0)发生;若满足

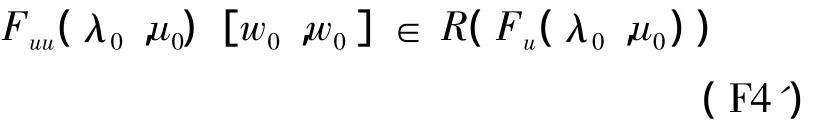
则λ'(0)=0且

其中θ为方程

Fuu(λ0，u0)［w0，w0］+Fu(λ0，u0)［θ］=0的解，则音叉式分歧在点(λ0，u0)发生.

1 Amplitude方程的化简

考虑一维Amplitude方程的稳态方程:

对第二个方程进行积分得到σv'+μ(u2)'=c(c为一个常数)，将x=0代入得到c=σv'(0)+ 2μu(0)u'(0)=0，进而σv+μu2=d(d为一个常数)，所以v=(d－μu2)，将v的表达式代入(2)的第一个方程，则方程(2)可以化简为

为了方便计算我们的问题，固定区域边界，做变量变换，把方程(3)变为

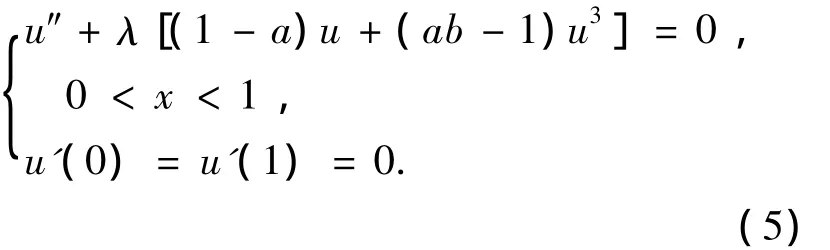
定义算子F:R+×X→Y，

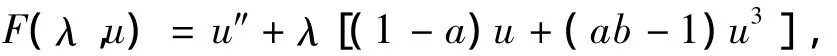
其中

2 主要结果

设f(u)=(1－a)u+(ab－1)u3.显然，对任意的λ∈R，均有F(λ，0)=0.下面我们应用定理1讨论当a与b取不同值时方程解发生分歧的条件.

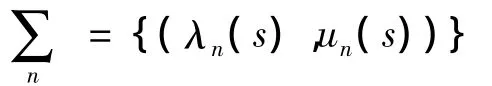
其中s∈(－ε，ε)，(λn(s)，un(s))为C∞的函数且满足λn(0)=λn，un(s)=sφn+◦(s).进一步，λn'(0)=0且当ab＜1时，λn″(0)＞0;当ab＞1时，λn″(0)＜0.

证明 验证定理1的所有条件.

(1)dim N(Fu(λn，0))=co dim R(Fu(λn，0))=1.

首先由特征值问题

将方程组(7)中第一个等式两边同时乘以φn，第二个等式乘以φ，然后两式做差并在［0，1］上积分，则有

所以知(F1)成立.

由Fλu(λn，0)［φn］=(1－a)φn，而(1－＞ 0，所以有 Fλu(λn，0)［φn］∉R(Fu(λn，0))知(F3)成立.

(3)Fuu(λn，0)［φn，φn］∈R(Fu(λn，0)).

由Fuu(0，λn，0)［φn，φn］=λnf″(0)φ2n=0

所以知(F4')成立.

(4)λ'(0)=0，λ″(0)≠0.

事实上，Fuu(λn，0)［φn，φn］=0，所以由定理1知λ'(0)=0，且θ=0，又

所以由定理1知

所以由定理1知当a＜1且1－ab＞0时，在(λn，0)点发生音叉式分歧.此时由于λ″(0)＞0，知正解的分歧为超临界的;而当a＜1且1－ab＜0时，由于λ″(0)＜0，知正解的分歧为次临界的.证毕.

［1］ Matthews PC，Cox SM.Pattern formation with a conservation law.Nonlinearity，2000(13):1293－1320.

［2］ Cox SM，Matthews P C.New instabilities in two－dimensional rotating convection and Magneto convection.Physica D，2001(149):210－229.

［3］ Norbury J，WinterM，Wei J.Existence and stability of singular patterns in a Ginzburg－Laudau equation coupled with a mean field.Nonlinearity，2002(15):2077－2096.

［4］ Crandall G，Michael Rabinowitz H.Paul Bifurcation perturbation of simple eigenvalues and linearized stability.Arch Rational Mcch Anal，1973(52):161－180.

［5］ Liu P，Shi J，Wang Y.Imperfect and pitchfork bifurcations. Jour Func Anal，2007(251):573－600.