基于两级Smith预估的纯滞后系统串级模糊控制仿真

刘寅东

(东北电力大学自动化工程学院，吉林吉林132012)

在工业生产过程中，纯滞后对象是普遍存在的，其影响结果是使系统会产生较大的超调量和较长的调节时间，使动态过渡过程变坏，进而系统的稳定性降低。在工程上，当对象的纯滞后时间τ与对象的惯性时间常数Tm之比大于0.5时，认为是具有纯滞后的过程，采用常规的PID控制器将很难获得良好的控制效果。

对纯滞后系统的控制算法，工程上常见的有PID控制算法、大林算法、Smith预估控制算法和智能控制方法等［1－4］。对于具有纯滞后的串级控制系统，普遍采用的控制方法是基于副回路Smith预估补偿的串级PID控制，即在副回路中加入Smith预估器，预先估计出副回路被控对象在干扰作用下的动态特性，然后由Smith预估器进行补偿，力图使被延时了τ时间的被控量超前反映到副调节器的输入端，使副调节器提前动作，从而明显的减小超调量和加速调节过程。但这种方法仅仅将滞后补偿到了副回路的外部，只加快了副回路的响应速度，滞后仍然在外回路的内部，控制效果并不是很理想。

针对上述问题，文献［5］提出了两级Smith预估补偿的控制方法，该方法虽然能使系统性能有一定提高，但是，还是有很大的超调量和很长的调节时间。为此本文利用模糊控制器与积分环节并联作为主调节器，由于而模糊控制器具有动态性能好、鲁棒性强特性的特点，可以克服对象模型不精确、对象参数时变的缺点，而以主副回路Smith预估器为辅，解决纯滞后问题，在保留原系统串级控制的基础上，形成一种新型的控制器。

1 两级Smith预估补偿器的设计

图1中，Gc2(s)为副调节器传递函数，G2(s)e－τs为副回路被控对象传递函数，模糊控制器与积分环节并联作为主调节器，其等效传递函数设为Gc1(s)，G1(s)为主回路被控对象传递函数，G2(s)(1－e－τs)和G0(s)(1－e－τs)分别为内回路和外回路Smith预估器。其中

图1 基于主副回路Smith预估补偿的纯滞后串级模糊控制系统结构

副回路等效传递函数为

外回路中含有Smith预估器的控制器的等效传递函数为

则图1所示的串级控制系统的传递函数为

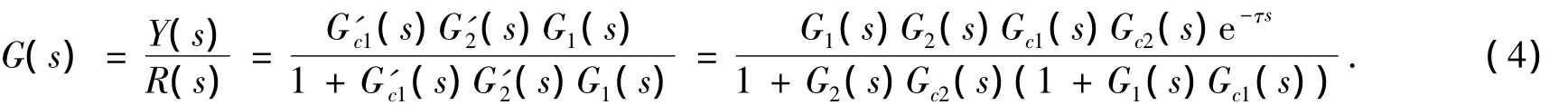
由上式可以看出，经过两级Smith预估器补偿后，系统的特征方程为

特征方程式中不包含e－τs，因此，纯滞后特性不影响系统的稳定性。

2 模糊控制器的设计

图2给出了模糊控制器的原理框。为简便起见，系统偏差、偏差变化率和输出的模糊集均为:负大(NB)、负中(NM)、负小(NS)、零(ZE)、正小(PS)、正中(PM)、正大(PB)。按经验均选三角形作为隶属函数曲线见图3。

图2 模糊控制器原理图

图3 模糊子集的隶属函数

模糊控制器是模糊控制系统中的核心部分，其控制规则根据有经验的专家和操作者的经验和知识制定出，控制规则如表1所示，采用的模糊推理算法为Mamdani的“最小—最大”推理法，模糊判决为重心法。

表1 模糊控制规则表

3 算法仿真研究

根据经验可知，对于串级控制系统，其副回路与主回路时间常数之比一般小于1 3。在仿真过程中为了方便比较，根据文献［5］取主副回路被控对象。主回路被控对象

副回路被控对象

纯滞后时间常数

主调节器采用模糊控制器与积分环节并联构成，这样可以解决系统静态偏差大的问题，其中积分环节增益为Ki1=0.07。模糊控制器是一个两输入、单输出二维模糊控制器，输入量为系统偏差E及偏差变化率EC，输出量为控制量U，它们的增益分别为Ke=1.3，Kec=4.9。副调节器采用PI控制器，调节器控制参数为Kp2=0.5，Ki2=0.08。

三种控制策略，基于一级Smith预估器的串级PID控制、基于两级Smith预估器的串级PID控制和基于两级Smith预估器的串级模糊控制的阶跃响应曲线如图4。

图4 系统的阶跃响应曲线

由图4知，基于两级Smith预估补偿的纯滞后串级模糊控制比另外两种控制策略的响应快，控制效果好。本文提出的控制方法应用于纯滞后串级控制系统，很大程度改善了系统的控制品质，增强系统的鲁棒性和抗干扰性，是一种有效的控制方案。

通过以上Matlab仿真比较得出三种控制的性能指标，见表2。从表2可以看出:基于两级Smith预估补偿的串级模糊控制比另外两种控制策略具有更好的效果，它使系统具有较好的动态特性;不仅调节时间短，而且无超调量，具有较理想的稳态品质，稳态过程无振荡，控制精度较高。

表2 三种控制策略性能指标

4 结论

本文提出的基于两级Smith预估补偿的串级模糊控制将串级控制方法与模糊控制、Smith控制相结合，来解决串级控制系统中存在的问题。仿真结果表明，将Smith预估器引入到串级控制系统的主副回路中，加快了主副回路的响应速度;引入模糊控制以后，控制效果得到了一定的改善，能得到更好的控制效果，调节时间大大缩短、无超调量、稳定性能增加。若被控对象数学模型发生变化后Smith预估器也发生了相应的变化，则系统的控制效果预计将会更好，进一步的研究将朝这个方向进行。

［1］程启明，王勇浩.基于Smith预估的模糊/PID串级主汽温控制系统仿真［J］.电工技术学报，2007，22(3):143－147.

［2］侯涛，董海鹰.基于T－S模型的倒立摆双闭环串级模糊控制设计与仿真［J］.系统仿真学报，2007，19(11):2477－2479.

［3］张立群，李东海，唐多元，薛亚丽.热力系统串级控制PID参数优化研究［J］.系统仿真学报，2005，17(8):1848－1850.

［4］喻桂兰.纯滞后系统变积分数字控制研究［J］.化工自动化及仪表，2010，37(7):17－20.

［5］刘川来，刘成才，李康康.纯滞后串级控制系统的两级Smith预估补偿［J］.青岛科技大学学报，2006，27(5):460－462.