基于IGA-SVM的汽轮机故障诊断研究

孙凯，田国清，田宏，段文超，田洋，陈立军

(1.东北电力大学自动化工程学院，吉林吉林132012;2.华能新华发电有限责任公司，黑龙江大庆163815;3.包头钢铁职业技术学院自动化系，内蒙古包头014010)

随着电力工业的迅速发展，电力设备自动化程度的不断提高，越来越多的大容量、高参数汽轮机组陆续投入运行，机组容量的增大使其结构和系统日趋复杂，不安全因素必然越来越多［1］。因此如何有效地提高汽轮机故障诊断的准确率，保证其稳定安全的运行是十分重要的。

近年来，专家系统、人工神经网络、聚类分析等多种方法被应用于汽轮机故障诊断中，并取得了一定成果［2－6］。由于汽轮机结构的复杂性和故障机理的多样性，这些故障诊断分析方法的有效性和准确性还有待提高。支持向量机(Support Vector Machine，SVM)是由Vapnik等人在统计学习理论的基础上建立起来的一种机器学习方法［7］，该算法很好地执行了统计学习理论的结构风险最小化原则，将其应用于故障诊断最大的优势在于它适合于小样本决策，其学习方法的本质在于能够在有限特征信息情况下，最大限度地发掘数据中隐含的分类知识［8］，如文献［9－11］将支持向量机应用于泵、汽轮机等故障诊断中。但支持向量机参数的选取比较困难，目前关于参数的选取还只是凭借经验。而遗传算法(Genetic Algorithm，GA)是一种智能搜索方法，它源于生物进化的模型。由于遗传算法具有强大的全局搜索能力，可以在很短的时间内搜索到全局最优点，所以应用遗传算法优化支持向量机的参数，以减少参数选择的盲目性，有效地提高支持向量机的分类识别能力。文献［12］将改进的遗传算法优化支持向量机寻找较优的SVM参数，并成功地将其应用于精馏塔故障诊断中，进一步提高了支持向量机的分类识别能力。

本文利用代沟选择和可变交叉概率的改进遗传算法(Improved Genetic Algorithm，IGA)优化支持向量机(Support Vector Machine，SVM)寻找较优的SVM参数，并将其应用到汽轮机故障诊断中。通过诊断实例表明，经IGA优化后的支持向量机分类模型较GA-SVM模型具有更高的分类准确率。

1 SVM算法介绍

1.1 SVM理论

支持向量机算法有效地改善了传统分类方法的缺陷，具有较强的理论依据，非常适合于小样本、非线性及高维模式情况下的分类问题，表现出很多优于已有方法的性能。

基于支持向量机算法进行分类的基本思想分以下五步:

Step1:首先给出训练样本

其中:xi∈Rn，yi∈{－1，+1}，i=1，2，…，l，n为样本空间的维数;

Step 2:选择合适的核函数并初始化惩罚参数C＞0;

Step 3:构造最优超平面对应的规划问题

求解得到α*=(，…)T，其中为对应的训练样本的支持向量;

Step 4:计算分类阈值b*，在开区间(0，C)中选取α*的一个分量，根据计算

Step 5:由w*和b*构造最优超平面(w*·φ(x))+b*=0，这样得到其对应的最优分类面的决策函数为

其中K(xi·xj)=φ(xi)·φ(xj)为满足Mercer核定理的核函数。

1.2 核函数的选择

核函数是支持向量机的重要组成部分，支持向量机常用的四种核函数:线性核函数、多项式核函数、高斯径向基核函数和两层感知器核函数［13］。对不同核函数的支持向量机的训练结果进行对比，实验表明，当采用高斯径向基核函数和两层感知器核函数时，支持向量机的分类效果相当，并且均优于采用线性核函数和多项式核函数的支持向量机分类效果［14］。由于在实际应用中高斯径向基核函数被广泛的采用，而两层感知器核函数的参数个数多于高斯径向基核函数，考虑到后续遗传算法优化核函数参数的复杂度，本文采用高斯径向基核函数，其中为2个向量间的距离，i=1，2，…，N，j=1，2，…，N，σ为宽度参数，高斯径向基核函数参数。

2 基于IGA优化SVM相关参数

遗传算法(Genetic Algorithm，GA)是基于达尔文进化论，在计算机上模拟生命进化机制而发展起来的搜索最优解方法。它根据“适者生存、优胜劣汰”等自然进化规则来进行搜索计算和问题求解。遗传算法对于复杂的优化问题无需建模和复杂运算，只要利用遗传算法的三种算子就能得到最优解。标准遗传算法是由染色体的编码、种群规模、适应度函数、遗传算子构成的［15］。

本文采用的改进遗传算法(IGA)与标准遗传算法(GA)的主要差别是在选择和交叉两步遗传操作上。选择操作中采用了代沟选择和基于适应度值的重插入，确保当前种群中最适应的个体总是被连续传播到下一代;交叉操作中采用可变交叉概率。

基于改进遗传算法的参数优化过程如图1所示。具体步骤如下:

Step 1:给定参数C、g的范围，并对其进行二进制编码。

Step 2:适应度评估。采用K－折交叉确认(K-fold Cross Validation)方法评估个体的适应度。

Step 3:设置初始种群数量，及最大进化代数。

Step 4:计算群体中各个体的适应度，检查是否满足终止条件，若满足，则结束寻优;否则转至Step 5。终止条件为连续几代种群不能再进化，最优个体的适应度相等或寻优达到最大进化代数。

Step 5:依次执行遗传算子操作。对于选择操作，使用随机遍历抽样，设置代沟ggap，根据适应度值从当前种群中选择m×ggap个个体复制到子代种群中。对于交叉操作，对选择操作中复制的子代种群进行单点交叉。对于交叉概率，本文采用动态参数法，这样做可以使进化后期优化的对象比较容易稳定，以减少无用计算。

Step 6:基于适应度值的重插入。由于使用了代沟，子代种群的数量比当前种群数量要小，用子代群体中的个体代替当前种群中最不适应的个体。基于适应度的重插入确保当前种群中m×(1－ggap)个最适应的个体总是被连续传播到下一代，并且每一代中不创建比现存种群多的个体，计算次数减少，内存要求也小。

Step 7:进化代数加1，检查是否满足终止条件，若满足，则结束寻优;否则转至步骤Step 5。

图1 改进遗传算法的SVM参数优化流程图

3 汽轮机故障诊断实例

本文利用ZT－3型汽轮机模拟转子实验台对汽轮机转子振动的四种典型故障(转子质量不平衡、转子动静碰磨、轴系不对中、支座松动)及无故障进行了模拟实验，提取175组数据进行试验分析，从中选取100组已知类别的故障样本进行训练，其余的75组数据作为测试样本。

为了使SVM训练和测试时能有效的区分出各故障类型，给各故障(这里暂且把无故障情况作为一种特殊的故障类型)赋予相应的类标签，如表1所示。

表1 故障类别与标签对应关系

本实验采用“一类对余类法”策略，利用遗传算法优化SVM参数的模型，对汽轮机各故障进行识别分类。分别采用改进遗传算法和标准遗传算法对SVM进行参数优化。IGA和标准GA的参数设置如下:C、g的范围为［0，100］，二进制编码长度为20，初始种群数量m=20，进化最大代数maxgen=100，变异概率pm=0.002;标准GA的交叉概率pc=0.4;IGA的代沟ggap=0.9，交叉概率的初始值pc=0.4。

图2给出了由IGA-SVM得到的分类准确率(目标函数)随进化代数的变化曲线，可以看出随着进化代数的增加，分类准确率趋近于恒定值96%，而此时得到的惩罚因子C为14.1562，核函数参数g为2.0975，终止进化代数为50。图3给出了由标准GA-SVM得到的分类准确率(目标函数)随进化代数的变化曲线，可以看出随着进化代数的增加，分类准确率趋近于恒定值90%，而此时得到的惩罚因子C为6.3183，核函数参数g为6.0768，终止进化代数为100。

由图2和图3可以看出，IGA-SVM方法进化到50代时连续几代最优个体的适应度相等，认为种群不能再进化，此时已达到最优的优化效果;而标准GA-SVM方法进化到了100代，达到了终止进化代数的条件，有可能没有达到最优的优化效果。可见IGA-SVM方法参数优化的效果明显优于标准GA-SVM方法优化的效果。

图2 IGA-SVM分类准确率随进化代数的变化曲线

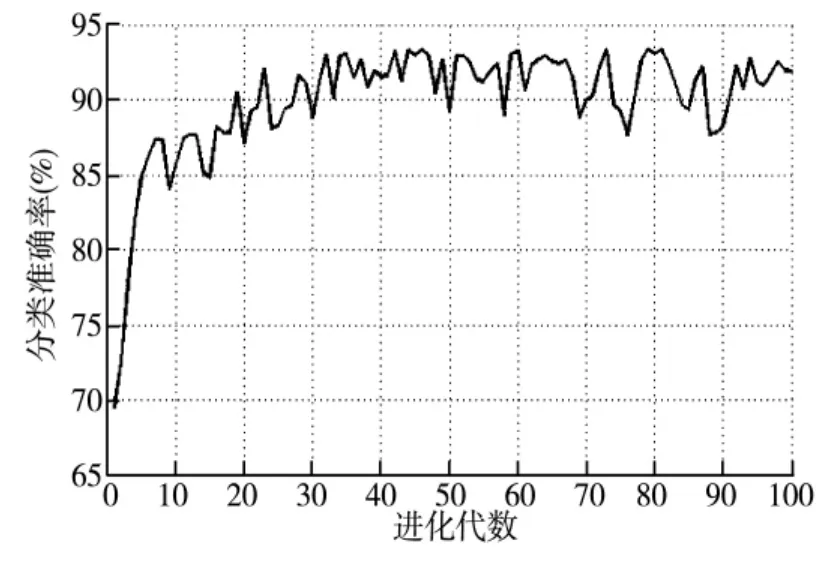
图3 标准GA-SVM分类准确率随进化代数的变化曲线

表2 IGA-SVM及标准GA-SVM故障识别结果

将IGA-SVM方法与标准GA-SVM方法得出的各故障识别结果进行了对比分析，结果如图4所示。由图4可以看出，除无故障情况外，IGA-SVM方法的各故障分类准确率均明显高于GA-SVM方法，说明利用改进遗传算法优化支持向量机的相关参数能有效的提高SVM多故障分类能力。

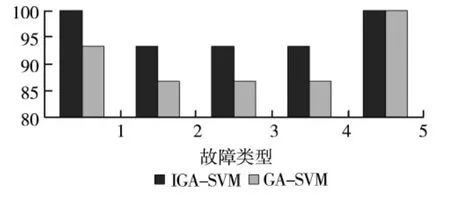
图4 两种方法分类准确率比较

4 结论

针对SVM参数选取困难的问题，本文采用改进遗传算法优化支持向量机分类模型的相关参数，并将其应用到汽轮机故障诊断中，通过与标准遗传算法优化的支持向量机分类模型比较，表明基于改进遗传算法优化支持向量机的模型能较好的对汽轮机故障样本进行分类，提高了故障诊断的准确率，对汽轮机故障诊断的实践有非常显著的指导作用。

［1］黄保海，李岩，王东风，等.基于KPCA和KFCM集成的汽轮机故障诊断［J］.电力自动化设备，2010，30(7):84－86.

［2］侯志花，张超，牛丽琼，等.基于专家系统的汽轮机振动故障诊断［J］.河北省科学院学报，2009，26(3):51－54.

［3］阮跃，徐世昌，黄文虎.汽轮机故障诊断专家系统的知识获取［J］.中国电力，1997，30(2):11－13.

［4］凌六一，黄友锐，魏圆圆.基于多传感器信息融合和神经网络的汽轮机故障诊断研究［J］.中国电力，2010，43(3):46－50.

［5］陈平，谢志江，欧阳奇.多层传递函数的量子神经网络在汽轮机故障诊断中的应用［J］.动力工程，2007，27(4):569－572.

［6］翟永杰，毛继佩，于丽敏，等.分级聚类支持向量机在汽轮机故障诊断中的应用［J］.华北电力大学学报，2003，30(6):25－29.

［7］V N Vapnik.Statistical Learning Theory［M］.NY:Wiley，1998:100－105.

［8］肖燕彩，陈秀海，朱衡君.遗传支持向量机在电力变压器故障诊断中的应用［J］.上海交通大学学报，2007，41(11):1878－1886.

［9］嵇斗，王向军，张民.基于支持向量机的电路故障诊断模型［J］.微计算机信息，2007，23(11):198－200.

［10］田路，田干，张炜，等.基于支持向量机的涡轮泵故障诊断方法研究［J］.控制工程，2007，14(S):138－140.

［11］张超，韩璞，唐贵基.基于K-L变换的支持向量机在汽轮机故障诊断中的应用［J］.汽轮机技术，2007，49(2):148－150.

［13］Simon Haykin著，申富饶，徐烨，郑俊，等译.神经网络与机器学习［M］.北京:机械工业出版社，2011:176－179.

［14］郑蕊蕊，赵继印，赵婷婷，等.基于遗传支持向量机和灰色人工免疫算法的电力变压器故障诊断［J］.中国电机工程学报，2011，31(7):56－63.

［15］张艳秋，王蔚.利用遗传算法优化的支持向量机垃圾邮件分类［J］.计算机应用，2009，29(10):2755－2757.