卫星对空间目标悬停的最优控制

顾大可

(东北电力大学自动化工程学院，吉林吉林132012)

近年来，随着航天技术的发展，目前空间技术正从空间利用提升为空间操作(或空间控制)，其中在交会对接、空间拦截撞击、在轨监视或者维修等方面的技术研究迅速发展。在空间操作中，有时候需要要求某个卫星相对于另外一个卫星、空间站或者大型航天器的相对位置始终保持不变，即追踪星位于目标星轨道的下方某个轨道上运动，并且要求追踪星和目标星的轨道相位与轨道角速度均相同，这样追踪星仿佛“悬停”在目标星的下方，但追踪星的轨道低于目标星的轨道。追踪星的轨道称为悬停轨道，这就是一个悬停问题［1］。在空间操作技术中，这种形式的卫星运动具有重要的科学意义和很大的经济价值，可以设计一个小卫星悬停在目标星下方，时刻监视目标星的飞行状态、外形结构、工作目的以及可以随时检查被追踪的飞行器是否正常工作，从而得到准确的信息并且减少一些不必要的费用，这是卫星的一个新的应用领域。

对于这样的追踪星悬停轨道，按照通常在地球引力场中的开普勒轨道设计其轨道根数显然是无法实现的。为此，本文从卫星相对空间目标的Hill方程出发，提出了悬停轨道的最优控制策略，即保证在连续推力控制最省燃料的情况下，卫星运行在新的悬停轨道上。主要目的是将悬停问题转化为带有终端状态约束的标准最优控制问题。虽然以前文献中有一些方法可以用来解决带有约束的最优控制问题。不过，这些方法是针对一般情况的，不是十分有效，如文献［2－5］中的方法。本文采用一种约束变换的思想将复杂的约束条件转换为可以求解的标准形式，这样我们获得一系列具有标准约束条件的最优控制问题，然后应用控制参数化思想和时间尺度变换技术设计了一个有效的计算方法来求解卫星对于空间目标悬停的最优控制问题，该方法的数值解可以利用最优控制软件包MISER3.2［6］来计算。

1 问题描述

1.1 悬停轨道动力学模型

Hill方程是在目标星轨道坐标系内研究追踪星相对于目标星的运动特性。其中坐标原点O在目标星质心，OY沿地球半径方向朝外，OX与OY垂直指向飞行的前方，并在目标星的轨道平面内，OZ与前两者构成右旋正交系(图1)。

图1 轨道坐标系示意图

设目标星的运行轨道为圆形，可以用下面的方程描述悬停的追踪星相对于目标星的运动方程:

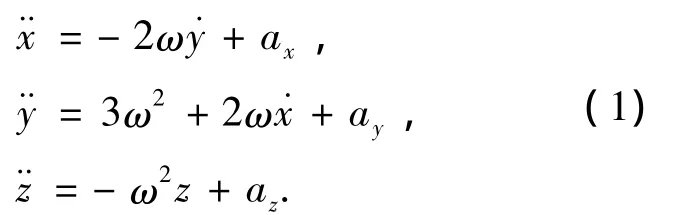
当连续推力使得在某一时刻tf，追踪星和目标星的相对速度和相对位置与时间有关项的系数均为零时，则可以实现悬停效果:

这样，目标星与追踪星的相对位置才能始终保持为

1.2 悬停燃料最省的控制问题

为了简单起见，我们主要考虑平面运动的情况。假设目标星和追踪星已处于共面的圆轨道上，令x=［xy］T，u=［axay］T，则系统的状态方程如下:

其中初始状态

终端状态

我们这里考虑的在固定时间段［0，tf］内，满足给定的边界条件即初始状态和终端状态，考虑控制过程中最省燃料，目标是使如下二次型性能指标最小:

其中，控制量满足如下约束umin≤ui≤umax，i=1，2。

综上我们可以归纳成如下的悬停最优控制问题:

问题P:对于系统(4)，满足初始约束条件(5)和终端约束条件(6)下，寻找控制u=［u1u2］T使得在满足控制约束的前提下，使性能指标(7)达到最小。

2 计算方法

我们给出有效地解决上述问题P的方法。首先将时间间隔［0，tf］分割成为np个子区间，其中np+1个分割点记作

对于每个分区间上构造如下式所示的分段常值控制器

其中:χ［τρk-1，τp

k)(t)是时间区间［)上的特征函数，其定义如下:

σ1ρ，k，k=1，2，…，np是控制参数，k=0，1，…，np是满足式(6)切换时间点。

记Γp为所有满足式(8)向量τp的集合。令。我们所讨论问题P的控制函数(t)、(t)表达形式如式(9)所示，这样把问题P记为问题Pp。

问题Pp:对于系统(4)，满足初始约束条件(5)和终端约束条件(6)下，寻找控制参数矢量和使得在满足控制约束的前提下，使性能指标(7)达到最小。

当p≥1时，问题Pp是一个关于和最优参数选择问题。性能指标J关于控制参数矢量和以及控制量的初值ζ1，ζ2的梯度很容易得到，详见文献［3］的定理5.2.1。事实上，根据定理5.3.1我们可以得到性能指标J关于切换序列的梯度公式，尽管这些公式对于数值计算不是很有效。因此本文引入时间尺度变换的思想把时间切换变量映射到固定的时间点。

引入一个新的时间变量s，则从不定的时间区间t∈［0，tf］到固定的时间区间s∈［0，1］的映射由如下微分方程给出

其中，初始和终端条件为t(0)=0和t(1)=tf，函数(s)称为强化控制，定义为

系统状态方程

并且满足如下的约束条件

综上所述，原始的卫星对于空间目标悬停的最优控制转化为一个参数优化问题，即非线性规划问题，利用SQP的数值优化算法即可求出卫星对于空间目标悬停的最优控制的最优解。

3 数值仿真

考虑目标星为地球静止轨道，即轨道半径为r0=42164.169 km，而追踪星与目标星运行在同平面的圆轨道上，初始条件x0=［-114.57615.460.0070］T，终端约束条件为xtf=［0-100000］T，推进系统能产生的加速度为≤0.5，i=1，2，终端时刻为tf=150 s，np=20，将［0，tf］分为20等份，利用最优控制软件包MISER3.2进行求解，仿真结果如图2所示。

图2 追踪星位置和速度的变化曲线

图2为追踪星的位置和速度随时间的变化曲线;图3为追踪星的x－y平面的最优悬停轨迹;图4为最优控制输入u1和u2随时间的变化曲线。由上面的仿真图可以看出，追踪星的终端位置和速度都达到了要求，并且运动轨迹较为平滑，整个悬停过程较为平稳。从图4可以得出控制输入满足给定的约束条件。综上，追踪星可以在本文设计的控制器作用下，满足控制约束就可以精确、快速地由初始位置转移到指定的悬停位置。

图3 追踪星x－y平面的最优悬停轨迹

图4 最优控制律u1和u2的变化曲线

4 结论与展望

本文给出悬停问题的最省燃料控制的解决途径，将悬停问题转化为带有终端状态约束的标准最优控制问题。进而我们把约束条件转化为标准形式，获得一系列具有标准约束条件的最优控制问题，然后应用控制参数化思想和时间尺度技术基础上设计了一个有效的计算方法。数值仿真表明本文提出的算法有效准确。

［1］Broschart S B，Scheeres D J.Control of Hovering Spacecraft Near Small Bodies:Application to Asteroid 25143 Itokawa［J］.Journal of Guidance，Control and Dynamics，2005，28(2):343－354.

［2］Goh C J，Teo K L.Control Parameterization:A Unified Approach to Optimal Control Problems with General Constraints［J］.Automatica，1988，24(1):3－18.

［3］Teo K L，Goh C J，Wong K H.A Unified Computational Approach to Optimal Control Problems［M］.London:Longman Scientific and Technical，1991.

［4］Miele A.Gradient Algorithms for the Optimization of Dynamic Systems［M］//Leondes C T.Control and Dynamic Systems:Advances in Theory and Applications.New York:Academic Press，1980:1－52.

［5］Sakawa Y，Shindo Y.On the Global Convergence of an Algorithm for Optimal Control［J］.IEEE Trans.Automatic Control，1980，25(6):1149－1153.

［6］Jennings L S，Teo K L，Goh C J.MISER3.2 Optimal Control Software:Theory and User Manual［DS/OL］.Perth:University of Western Australia，1997.http://www.cado.maths.uwa.edu.au.