最大熵原理与假设检验方法探讨

张凤宽

（天津商业大学 理学院，天津 300134）

0 引言

在沈世镒教授的文章[1]中给出了一种改进的经验分布函数的定义，使之更适用于Shannon熵的计算，并利用推导出的有关结果及最大熵原理给出了一个分布检验的新方法，即《分布的熵—矩检验法》。为了使这种方法的应用更广泛，本文拟将一维推广到二维及至多维的情形。

1 二维经验分布函数

对于任意给定的二维随机向量(X,Y)的样本为了给出它的经验分布函数，我们先进行如下讨论：

从(1)式出发可以得到一维样本x1,x2,..xm，排序后得x[1]≤x[2]≤...≤x[m],相应地有：

即 {(x[i],yx[i])}(i=1,2...,m)为(2)中的所有样本，取0＜α＜1/4 ，记 n=m12,n1=m1/2+α,n2=m1/2-α,显 然n2=m,n1.n2=m,定义[1]（带“^”者均为经验分布，以后出现“^”意思相同，不再叙述）

为X的Ⅱ型经验分布函数。

相应的有分布密度函数：

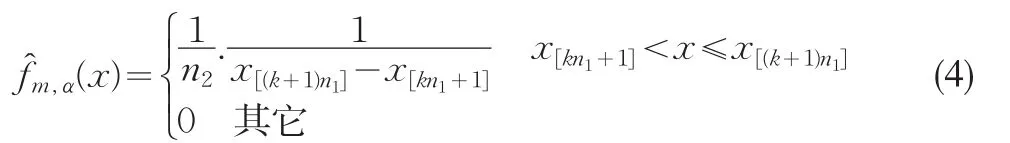
对于每一个k(0≤k≤n2-1):x[kn1+1],x[kn1+2],..x[kn1+n1]对应于(2)中的

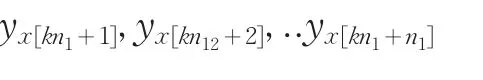
排序得：

取 0＜α'＜1/4，记 n0=n11 2,n3=n11/2+α',n4=n11/2-α',从而n3.n4=n1,=n1（显然m→∞时，n1=m1/2+α→∞）。

定义

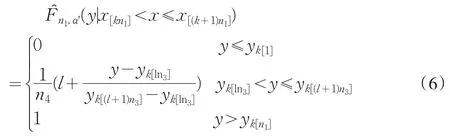
为y关于x的条件经验分布函数。

相应的分布密度函数为：

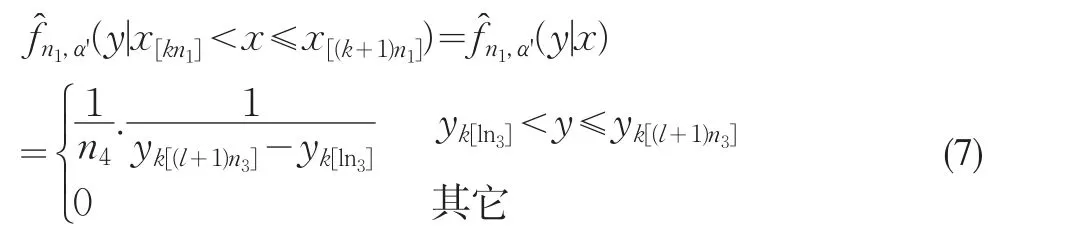
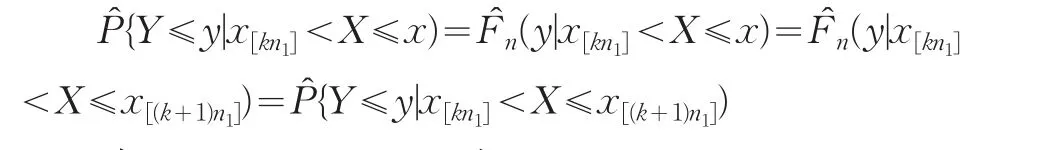
当 x[kn1]＜x≤x[(k+1)n1]时。

所以当 x[kn1]＜x≤x[(k+1)n1],yk[ln3]＜y≤yk[(l+1)n3]时，有：

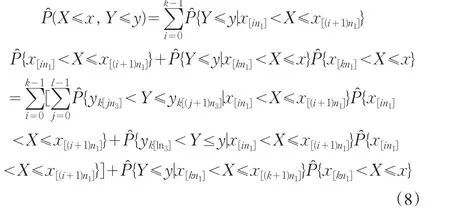
将(3)、(6)式代入(8)式即得二维随机向量的经验分布函数：

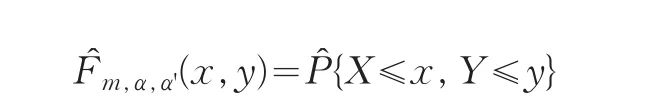
其相应的分布密度函数为:

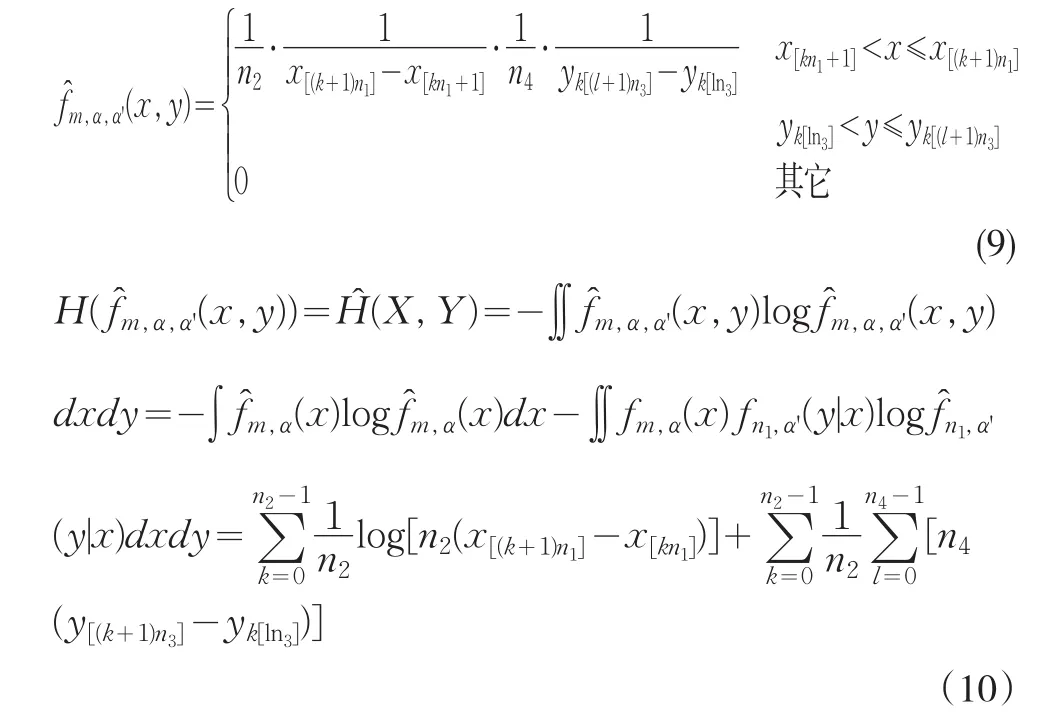
不妨假设(1)式中的样本是来自分布密度函数为f(x,y)的总体中，下面讨论 f̂m,α,α'(x,y)与 f(x,y)之间的关系。

定理1如果 f(x,y)为支集S上的分布密度函数且为二元连续的。其条件分布密度函数 f(y|x),f(x|y)关于x,y有一致有界导数，其边际分布密度函数 f1(x),f2(y)分别具有一致有界的导数，且在S上 f1(x)＞0,f2(y)＞0，则对任何，有

证明：

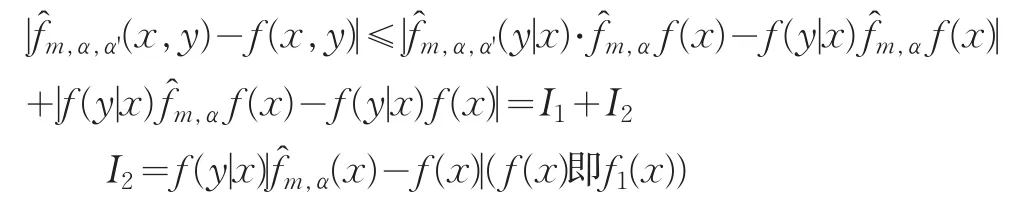
由已知条件 f(y|x)关于 x,y有一致有界导数，而∫f(x,y)dy=1，从而 f(y|x)有界。又由[1]中结论：当 f1(x)有一致有界导数时：

所以：

同时由 f1(x)有一致有界导数及∫f1(x)dx=1知 f1(x)有界。从而由(12)式知：

对于任意给定的x0：对应于每一个固定的m。有且仅有一个k，使得x[kn1]＜x0≤x[(k+1)n1]，所以：

而对于(15)式中的每一个(x[kn1],x[(k+1)n1]]，当m→∞时，n1→∞。且(x[kn1],x[(k+1)n1]]→x0

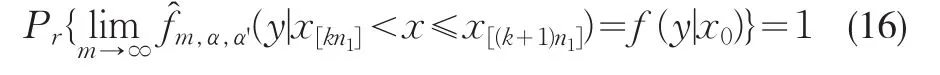
证毕。

从（1）式出发又可以得到一维样本y1,y2,...,ym，按照定义的方法可以得到关于y的经验分布密度函数，同样与类似定义可得到

定理2在定理1的条件下，若∫f(y|x)|logf(y|x)|dy存在，∫f(y|x)|logf(y|x)|dy关于x一致有界（以概率1），则：

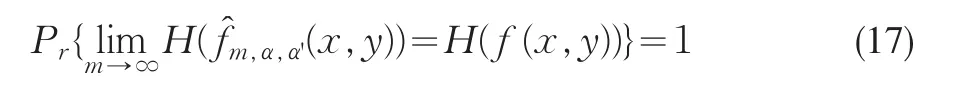
证明：

由文[1]的结论有：

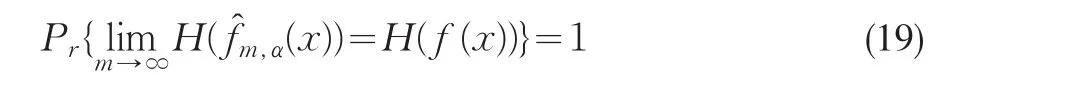
可知：

由于∫f(y|x)logf(y|x)dy以概率1关于x一致有界，故存在M1＞0，使得

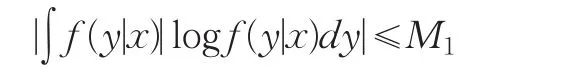
再考虑(12)式即知：

对于任意给定的x，由∫f(y|x)|logf(y|x)|dy的存在性及的证明过程，可用(15)～(16)式的极限方法证得：

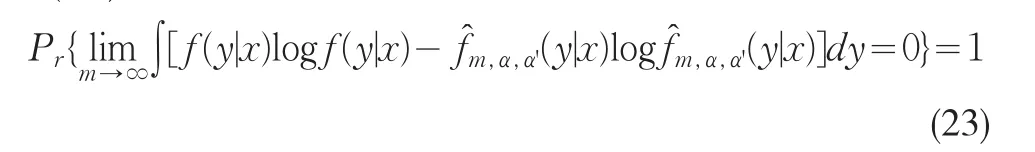
考虑(14)式即有：

由(20)、(21)、(24)式即知：

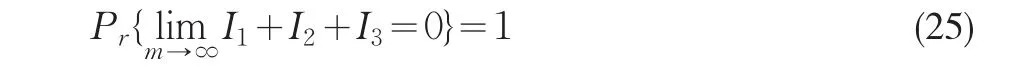
定理2证毕。

3 多维的情形

已知多维随机向量(x1,x2,...xn)(n≥3)的样本序列为：从上述讨论看出，可以从二维样本(x11,x21),(x12,x22),...(x1m,x2m)出发首先得到m,α,α'(x1,x2)（见（6）式）及相应的（见（7）式），对于每一个给定的k及l，有x3的相应样本序列(xkl[1],xkl[2],...xkl[n3])

然后与一维推广到二维完全类似，按照(6)～(9)式的定义方式可以得到：

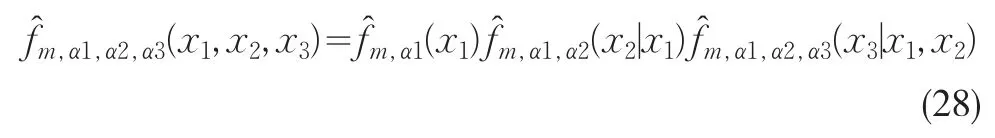
对于n维情形，可通过

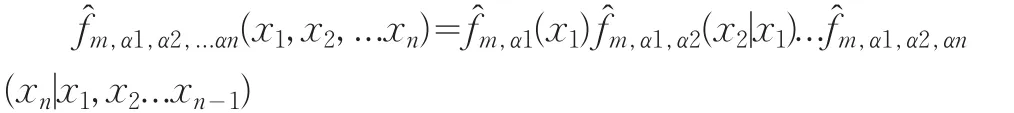
4 最大熵原理与假设检验

由此可见，在某些条件下，当且仅当分布密度函数属于指数分布族时其熵达到最大。所以以下的讨论都是在指数分布族中进行。

例1：如何判别一个多元样本序列

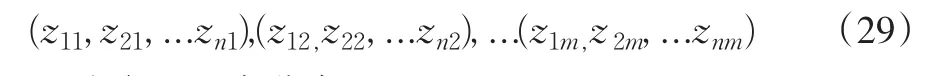
是否服从多元正态分布。

首先从（29）式出发计算数学期望和方差估计值：

当然如果期望和方差均为已知或者二者之一为已知，则不必再计算其估计值。

记 X=(x1,x2,...xn)',A=,B=,（如果ai,bij为已知，则令

如果随机向量X服从多员正态分布，则其相应的B=(bij)为正定阵，从而有非奇异阵L，使B=LL'，对应于A,B的n元正态分布密度Nn(A,B)为:

由此 f(x1,x2,...xn)可以计算出:

对(31)做如下线性变换:

则逆变换为:

变换（34）的雅可比行列式为:

因此:

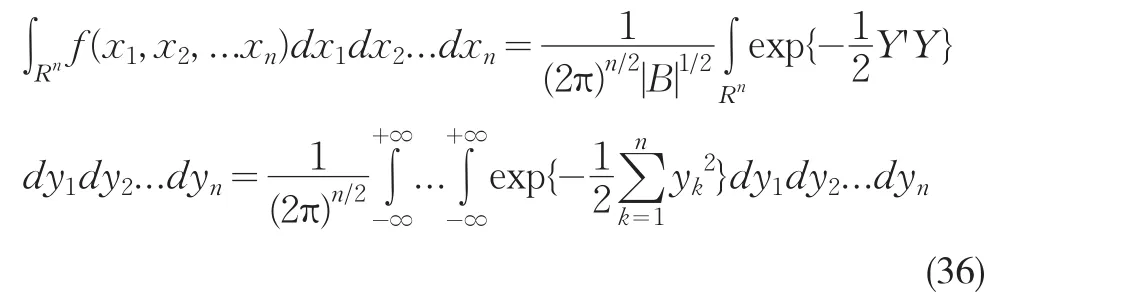
由此即知以 f(x1,x2,...xn)为分布密度的多元正态随机向量的模拟数据可以从标准正态分布的模拟数据求得，

即：如取作为n个独立模拟的标准正态随机变数据序列（这种序列可以从（0,1）上均匀分布的模拟数据得到，具体模拟方法见[6]）。经过变换（34）式所得到的X的相应序列:

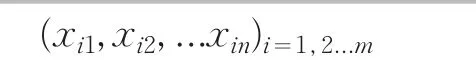
即为服从Nn(A,B)的多元正态随机向量序列。关于这一点从（31）～（36）的推导过程中易见。对于不同的（37）中序列就有对应的（38）中的不同序列（服从Nn(A,B)）,并且可以有无穷多组不同的序列（37）、（38），不妨取（38）中的100组。计算其相应的(j=1,2,...100)再与（32）式比较即得Δj=-Hj(f)|(j=1,2,...100)从Δj中依次挑出11个最大值[3]，将它们从大到小排列，分别记为Δm0,Δm1,...Δm10，取Δm1,Δm2,Δm5,Δm10为样本容量为m时的拟显著水平α=0.01,0.02,0.05,0.10的临界值。此即可作为Δ=|H(f̂)-H(f)|当 f为n元正态分布密度时的判别标准。增大样本容量m或增加模拟次数均可提高这种标准的精确度。

对于指数分布族中的其它的连续型向量也可以做类似于例1的处理，即先计算Shannon熵的精确值H(f)，再从样本出发计算H(f̂)，通过模拟得到一个Δ=|H(f̂) -H(f)|的判别标准。

上述判别法的缺点在于造表（即Δ的大小判别标准或对应临界值表）时比较麻烦，但是具体用表时比较简易。从样本出发计算H(f̂)时在计算机上较易实现。对维数较低的随机向量这种方法精确度较高，从而比高维时更适用。

[1]沈世镒.关于Shannon熵的统计计算及其在分布检验中的应用[J].高校应用数学学报,1988,12.

[2]Jhon,Willy S.Kullback.Information Theory and Statistics[M].New York:Wiley,1959.

[3]沈世镒,张润楚,肖芸茹.熵矩检验法与熵矩检验表[D].南开大学, 1985.

[4]张润楚.多元统计分析[M].天津：南开大学出版社,1986.

[5]林畛.变分法与最优控制[M].哈尔滨：哈尔滨工业大学出版社, 1987.

[6]肖芸茹.概率统计计算[M].天津：南开大学出版社,1986.