含有周期性的时间序列中随机型缺失数据的填补方法*
张 熙 李济宾 张晋昕△
在医学科研工作中,按一定时间间隔对客观事物进行动态观察,由于随机因素的作用,各次观察的指标X1,X2,X3,…,Xi,都是随机的,这种按时间顺序列排列的随机变量(或其观测)称为时间序列。应用时间序列模型进行预测在医学研究中已经很普遍〔1〕,但是时间序列在医学中的应用也面临一些困境。对时间序列数据建立数学模型时,序列太短会有损参数估计的稳健性,取较长序列则可以保证拟合模型的可靠性〔2〕。而实际情形是,序列涵盖的历史值越长,序列中越有可能含有缺失数据。即使加强质量控制,也不能完全避免。缺失数据的存在使时间序列建模出现困难,成为时间序列在医学研究领域应用的瓶颈。如果忽略缺失数据、直接跳过,将获得的观测值的先后次序当作时间次序来建模,势必得到错误的拟合模型。
有不少学者针对时间序列的缺失数据进行了有益的尝试,主要有:随机回归填补法、趋势得分法 (Propensity Score,PS)、马尔科夫链蒙特卡罗法 (Markov Chain Monte Carlo,MCMC)和三次样条插值法等〔3-5〕,但是这些时间序列缺失值填补方法都没有充分利用时间序列的频域信息。为此,本课题组提出基于周期信息的时间序列缺失值填补方法,本文从缺失比例与序列长度两个方面对填补方法进行模拟研究和评价。
方 法
1.模拟序列
在SAS9.1〔6〕环境下,采用模型(1)生成含有周期性的随机模拟序列:

通过电脑预实验,将随机型缺失的比例设置为10% ~50%,每隔10%设置一组数据,共五组数据,每组数据的序列长度为250;序列长度设置为30、50、100、200、250,共五组。
2.基于周期信息的时间序列缺失值填补方法(简称周期性填补法)
基本思想:基于序列的多个隐含周期,以相应的周期图峰值作为权重,计算不同周期位置的加权均数来填补缺失值。(1)通过周期图峰值检验搜索序列的多个隐含周期值;(2)基于不同的周期值,获得不同周期位置上原始数据的均数,并以该缺失位置上的均数作为该位置的初始填补值;(3)以不同的周期值相应的峰值作为权重,获得缺失位置上初始填补值的加权均数;(4)用一次填补之后的完整序列再次进行周期性检验;(5)将以上步骤循环迭代,直到前后两次填补值的相对误差不超过0.10时,循环停止,获得最终的序列填补值。
3.填补效果的评价
通过模拟周期性时间序列数据并构造随机型缺失,利用普通的spline插值填补法与周期性填补法,比较相同序列长度不同缺失比例、相同缺失比例不同序列长度下两种方法的缺失值填补效果。选用均方根误差(root mean square error,RMSE)以及标准化均方根误差(normalized root mean square error,NRMSE)〔8〕作为填补效果的评价指标:
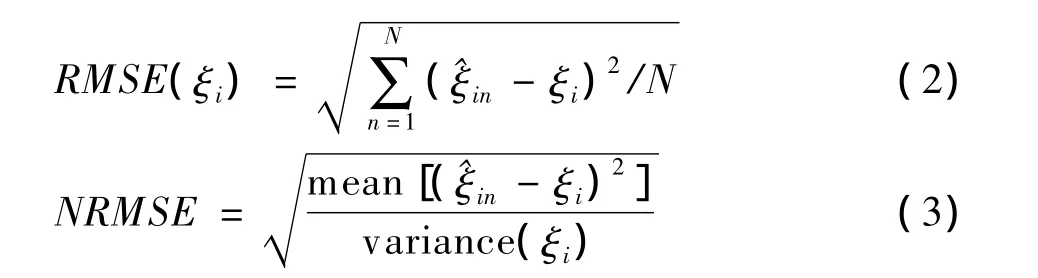
^
ξin表示第n次模拟得到的第i个缺失值的填补值,ξi表示第i个模拟缺失值的真实值,N表示一共进行N次模拟,本研究中N=100。
结 果
1.相同序列长度不同缺失比例下两种填补方法的效果比较
表1~2给出了样本含量是250,缺失比例分别为10%~50%时两种缺失值填补方法的NRMSE和RMSE的比较结果。
经配对资料的t检验比较,不同的缺失比例情况下,两种填补方法的NRMSE之间的差异均有统计学意义(P<0.001),由此认为不同缺失比例下两种填补方法的NRMSE值不同,填补效果有差异。不同的缺失比例下,两种方法的RMSE值居于不同水平,但是缺失比例为30%时两种方法之间的差异无统计学意义。
图1显示不同的缺失比例下,两种方法填补值的填补误差NRMSE与RMSE的均数变化情况。随着缺失比例的增加,两种方法填补值的填补误差N RMSE与RMSE均增高,但是 spline填补值的 NRMSE和RMSE值始终处于周期性填补方法上方(位置居于上方提示误差较大),即周期性填补的效果始终比spline插值填补法的效果好。
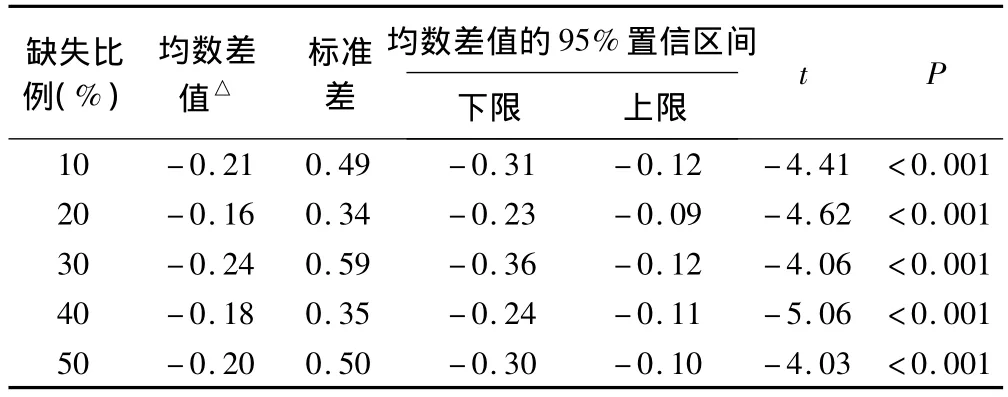
表1 模拟随机型缺失序列不同缺失比例下NRMSE比较
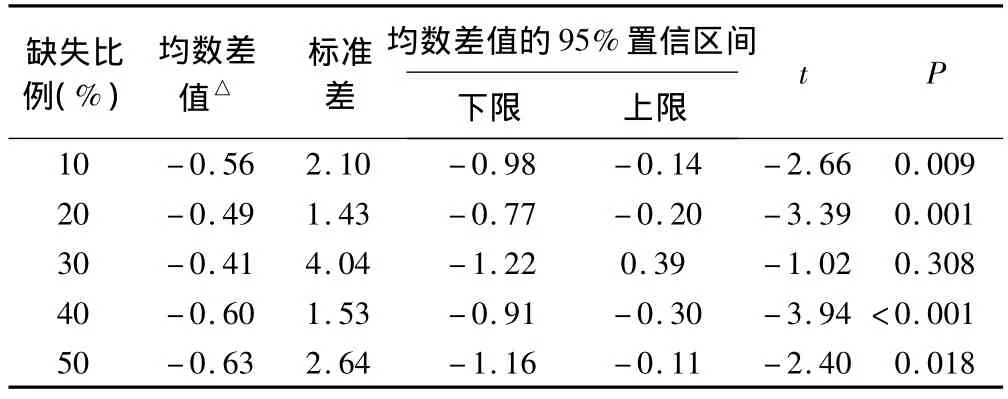
表2 模拟随机型缺失序列不同缺失比例不同填补类型RMSE比较
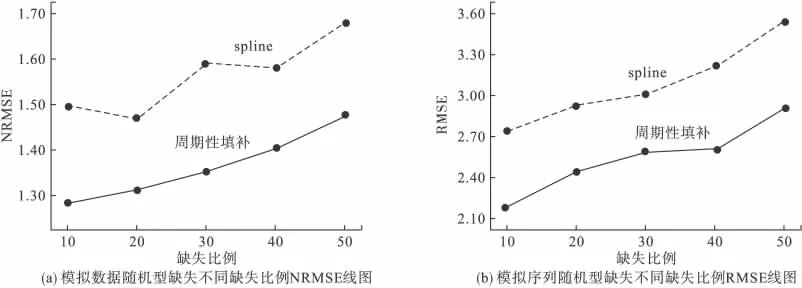
图1 不同缺失比例下填补值的NRMSE与RMSE的比较
2.相同缺失比例不同序列长度下填补效果的比较
经配对资料的t检验比较,在缺失比例相同,但是序列长度不同情况下,两种填补方法的 NRMSE和MRSE的差异,在序列长度较长时居于不同水平;而序列长度小于100时,两种填补方法间的差异无统计学意义。和RMSE的变化情况。随着序列长度的增加,两种方法填补值的NRMSE均降低,提示在序列长度比较短的时候两种填补方法的效果逊于序列长度较长时。但是spline填补值的NRMSE值始终处于周期性填补方法上方(位置居于上方提示误差较大),即周期性填补效果始终比spline好。RMSE的结果与NRMSE的结果基本一致。
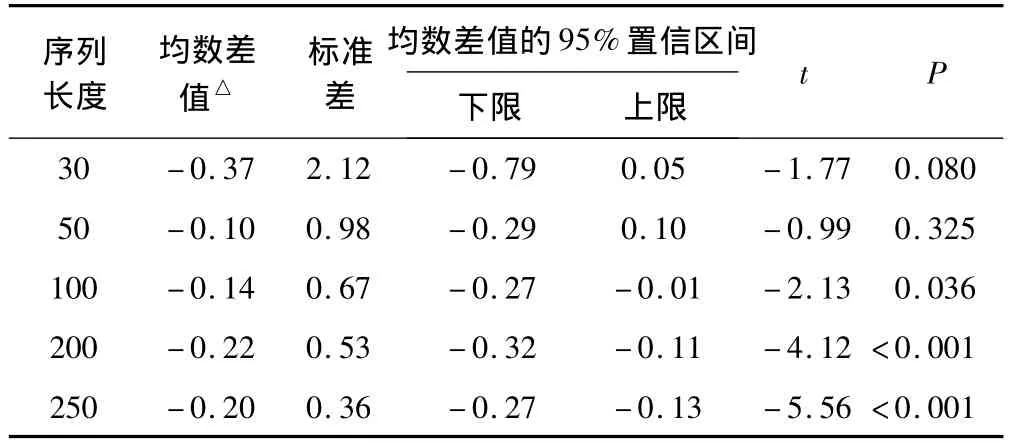
表3 模拟随机型缺失不同序列长度序列两填补方法NRMSE的比较
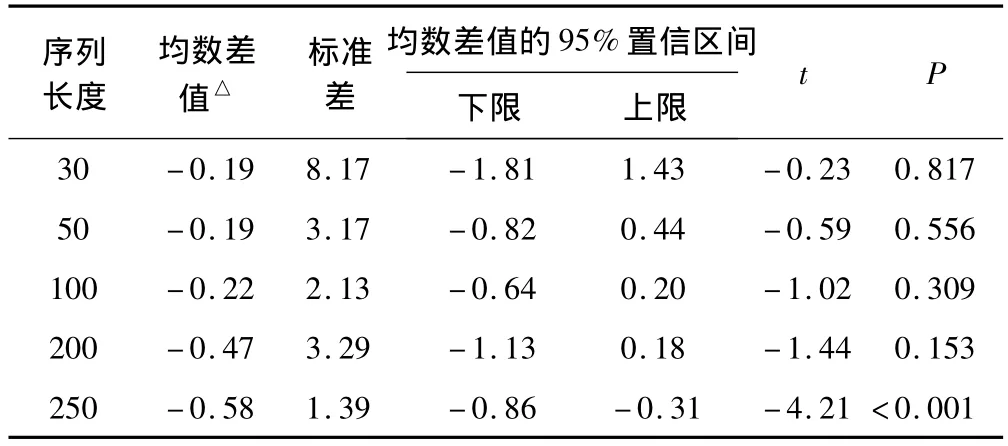
表4 模拟随机型缺失不同序列长度序列两填补方法RMSE的比较
图2显示,相同缺失比例不同序列长度下NRMSE

图2 相同缺失比例不同序列长度下填补值NRMSE和RMSE的比较
讨 论
本研究从相同序列长度不同缺失比例和相同缺失比例不同序列长度两个方面对时间序列缺失值周期性填补法和spline插值填补方法的填补效果进行比较。结果显示:相同序列长度不同缺失比例下两种填补方法的填补效果有差异;随着缺失比例的增加,两种填补方法填补值的NRMSE和RMSE均增加,填补效果随着缺失比例的增加而变差,但周期性填补法的效果始终优于spline填补法,而且两者的差别不会随着缺失比例的增加而变化。此外,序列长度对缺失值填补的效果也有一定的影响。模拟数据显示:在相同缺失比例不同序列长度的情况下,两种填补方法填补值的NRMSE和RMSE均随着序列长度的增加而减小。而且,在序列长度较长时,周期性填补方法的填补效果优于spline填补法。
针对时间序列中的缺失值问题,本研究提出一种基于时间序列蕴含的周期信息,以不同周期的谱峰值作为权重调整获得时间序列的填补值的方法,将时间序列时域和频域信息融合应用于时间序列缺失值的填补过程中,具有时间序列缺失值填补的个性化特点。模拟数据研究结果显示,本方法缺失值填补效果于spline插值填补法。但是,对于时间序列中随机型缺失数据的处理,需要同时考虑序列长度与缺失比例,对于序列长度较短,或者缺失比例较大的序列,本研究提出的周期性填补法和被普通应用的spline插值填补法的效果均较差。这种情况下,需要审慎地考虑缺失数据的处理,因为即使填补了缺失值,效果也比较差,有可能拟合错误的模型,扭曲序列的真实联系。effects for missing values between imputation method based on periodicity and the cubic spline curve method using simulating time-series data with periodicity.Methods To produce stable and periodic time-series within random missing values,and compare the imputation effect of two methods under the condition of the same sequence length,different missing percentage and the same missing percentage,different sequence length.The NRMSE(Normalized Root Mean Square error)and RMSE(Root Mean Square Error)is used to estimate the imputing effectiveness.Results Under the same sequence length,the imputation error of two methods increased according to the missing percentage.Except for RMSE in 30%,the NRMSE and RMSE was smaller than those of the spline method(P <0.05).Under the same missing percentage,the difference of error for two imputation methods was no statistical significance when the sequence is short,while the effectiveness of imputation method based on periodicity was better than that of the spline method when the sequence is long.Conclusion In general,the effectiveness of imputation method based on periodicity is better than that of the spline method in time series with significant periodicity.
1.方兆本,李红星,杨建萍.基于公开数据的SARS流行规律的建模及预报,数理统计与管理,2003,22(5):48-57.
2.Pascal Bondon.Infuence of missing values on the prediction of a stationary time series .Journal of time series analysis,2005,26(4):519-525.
3.封建湖,车刚明,聂玉峰.数值分析原理.北京:科学出版社,2001.
4.Wayne F.Velicer,Suzanne M.Colby.A Comparison of Missing-Data Procedures for ARIMA Time-Series Analysis.Educational and Psychological Measurement,2005,6 5:596-615.
5.Koji Mutekia,John F.MacGregora,Toshihiro Ueda K,et al.Estimation of missing data using latent variable methods with auxiliary information.Chemometrics and Intelligent Laboratory Systems,2005,78:41-50.
6.高惠璇等编译.SAS系统SAS/ETS软件使用手册.北京:中国统计出版社,1998:65-460.
7.Heikki Junninena,Harri Niskaa,Kari Tuppurainenc,et al.Methods for imputation of missing values in air quality data sets.Atmospheric Environment,2004(38):2895-290.
8.武艳强,黄立人.时间序列处理的新插值方法.大地测量与地球动力学,2004,24(4):43-47.

