常用正交表的构造原理及SAS实现

华中科技大学同济医学院公共卫生学院流行病与卫生统计学系(430030)

陈远方 林曦晨 徐利华 汤洪秀 汪宏晶 尹 平△

正交试验是通过一套规格化的正交表将各试验因素、各水平进行均匀搭配，只需较少的样本量即可找出最优组合，具有试验次数少、效率高、设计简便等特点，已被广泛应用于医学等研究领域〔1－3〕。但正交表种类繁多，各种类型的构造原理不同且复杂，特别是混合正交表，操作过程很是繁琐〔4－5〕。同时，目前缺乏采用通用软件生成正交表的文献介绍。为此，本文详细分析了正交表的构造原理并进行了分类，采用SAS软件构建了常用正交表的程序模块，极大地降低了正交试验中建立正交表的难度，方便实用。

方法和原理

1．2水平正交表

(1)哈达玛矩阵直积法构造N=2s型

N=2s型的2水平正交表任意两列都是正交的，而且每一列都与全1列正交。假设A，B分别为n×m与s×t矩阵，将A的每一个元素都乘以矩阵B而得到的ns×mt矩阵，用A⊗B表示，叫做矩阵A与B的直积。当A与B都是元素为±1的哈达玛矩阵时，由直积的意义和运算规则可知:

则A与B的直积也是哈达玛矩阵。应用上述构造标准哈达玛矩阵中，除全1列外，其任意两列与全1列都正交。因此，去掉全1列，就得到N=2s型的2水平正交表〔6〕。

(2)哈达玛矩阵特征函数法构造N≠2s且N=2(p+1)(p为素数且p≡3(mod4))型

特征值函数法利用的是构造2(p+1)阶哈达玛矩阵的思想，建立有限域 GF(p)={0，P-1，P-2，…，1}，利用有限域GF(p)的元根，构造R矩阵，然后构造K矩阵，再构造出2(p+1)阶方阵为哈达玛矩阵，最终构造出2(p+1)阶正交表。

当N≠2s且 N=2(p+1)型(p为素数且 p≡1(mod4))时，令N=2(p+1)，构造pn阶有限域GF(p)={0，P-1，P-2，…，1}，并给出 GF(p)的一个元根。把有限域GF(p)中每一个非零元素都表示为元根的方幂，由特征函数求出所有的

=2(p+1)E2(P+1)

即2(p+1)阶方阵为哈达玛矩阵。

在上面构造的2(p+1)阶哈阵中，把P+2行和P+2列，全部乘以-1。然后去掉全1列，再把矩阵中-1改成2，便构造出了N≠2s且N=2(p+1)(p为素数且 p≡1(mod4))类型的2水平正交表〔7〕。

2．Lt2(tm)型正交表

Lt2(tm)型正交表一般可采用正交拉丁方法进行构造。先建立正交拉丁方完全组，然后带入基本列，就可以得到相应的正交表了。建立正交拉丁方完全组的方法有多种，常用的有如下两种。

(1)素数或素数幂法

设n为任意一个素数或素数幂，GF(n)为n阶有限域，而 a1，a2，…，an与 b1，b2，…，bn为域中全体元素任意两列排列;c1，c2，…，ci为域中的全体非零元素，则可建立n阶正交拉丁完全组为

为构成的n阶正交拉丁方完全组〔8〕。

对建立的正交拉丁方完全组带入Li2(tm)型前两列的基础列便构造出了Li2(tm)型的正交表，即

3．水平数为素数幂的混合正交表

水平数为素数幂的混合正交表的构造通常采用并列法，是一种由标准表构造水平不同正交表，可以安排水平数不等的正交试验的常用方法。数学原理是并列性定理。

设Ln(S1×S2×…×Sn)型正交表A=(λij)的第j1和j2列(j1≠j2)的交互组{第 L1列，第 L2列，……，第Lι列}是完备的，将第j1和j2列按下列新规则φ合并成“新列”:

这里，φ 是集合 Γ ={(u，v):u=1，2，…，Sj1，v=1，2，…，Sj2}到结合 P={1，2，…，Sj1× Sj2}上的一一映射。则新列~λ和A中去除第j1，j2，L1，…，Lι后一起组成的矩阵就是利用并列法所构造的混合型正交表。

SAS实现

1．N=2s型的2水平正交表的SAS实现

为了更加通俗介绍SAS软件实现哈达玛矩阵直积法构造2水平正交表过程，本文以L16(215)为例进行详细阐述，运用SAS中IML模块创建标准哈阵，然后将标准哈阵去除第一列即全1列，且将-1写成2，便得到了L16(215)的正交表，结果见表1。SAS程序与解释如下，数据集zj2即为所求的正交表L16(215):

%let N=16;/*宏变量N表示试验次数*/

%let J=a@a@a@a;/*符号@表示矩阵直积*/

proc iml;/*运用IML模块创建标准哈达玛矩阵*/

a={1 1，1－1};/*a为最简单的二阶哈达玛矩阵*/

d=＆J;

create zj from d;/*用create语句的from选项创建SAS数据集zj，即所求的标准哈阵*/

append from d;

close zj;

quit;

data zj2(drop=i col1);/*将标准哈阵去除第一列，且将-1写成2，便得到了L16(215)的正交表数据集zj2即为所求*/

set zj;

array col(＆N);

do i=2 to＆N;

if col{i}=－1 then col{i}=2;

end;run;

proc sort;

by col2 col3;

run;

在SAS程序中只需修改两个宏变量N(试验次数)和J(哈达玛矩阵直积)，就可以构造 L4(23)、L8(27)、L32(231)等等N=2s型的2水平正交表。例如正交表L8(27)，此时N=8时，J=a@a@a，即 a的个数等于s，a表示最简单的哈阵，a与a之间用@连接。

表1 L16(215)正交设计表

2．N≠2s且 N=2(p+1)(p为素数且 p≡1(mod4))型的2水平正交表的SAS实现

以L12(211)为例，根据 N=2(p+1)得 p=5，2为有限域GF(5)的一个元根，SAS程序构造思路为:构造R阵→K阵→H12阵→正交表L12(211)，生成数据集zj即为所求的正交表L12(211)，结果见表2，程序如下。

%let n=12;/*宏变量n为试验次数*/

%let yg=2/*宏变量yg代表有限域的最小元根*

%let k=%eval(＆n-1);/*宏变量 k为试验因素，由于构造的是饱和正交表，其值也等于n-1*/

%let p=%eval(＆n/2-1);/* 宏变量 p，等同于GF(p)中的p，其值等于n/2-1*/

%let p1=%eval(＆p+1);

proc iml;/*根据R阵的数学排列规律运用proc iml模块构造数据集a*/

a=j(＆p，＆p，0);do i=1 to ＆p;do j=1 to ＆p;

if i＞ j then a［i，j］=mod((i-j)，＆p);

else;if j＞ =i then a［i，j］=mod((＆p+i-j)，＆p);

end;end;create a from a;append from a;close a;quit;

data R(keep=b1-b＆p);/*利用数据集a生成数据集R，即为R阵*/

set a;array a{＆p};array col{＆p};array b{＆p};do i=1 to＆p;if col{i}^=0 then do;n=1;do until(y=col{i});y=mod(＆yg．＊＊n，＆p．);n+l;end;a{i}=mod(n －1，2);end;else if col{i}=0 then a{i}=．;if a{i}=0 then b{i}=1;else if a{i}=1 then b{i}=-1;else if a{i}=．then b{i}=0;end;run;

data c(drop=i);/*创建K阵中除R以外的部分*/

b0=0;array b{＆p};do i=1 to ＆p;b{i}=1;end;

run;

data K;/*合并数据集c、R生成K阵*/

set c R;if b0=．then b0=1;

run;

proc iml;/*生成单位矩阵E阵*/

I=I(＆p1);create E from I;append from I;quit;

data KE1(keep=k11-k1＆p1 k21-k2＆p1);/* 数据集KE1为H12的上部分，即K+E和K－E*/

merge K E;array b{＆p1}b0-b＆p;array col{＆p1};array k1{＆p1};array k2{＆p1};do i=1 to＆p1;k1{i}=b{i}+col{i};k2{i}=b{i}-col{i};end;k21=k21*-1;

run;

data KE2(drop=b0 － b＆p col1 － col＆pli);/* 数据集KE1为H12的下部分，即K-E和-K-E*/

merge K E;array b{＆p1}b0-b＆p;array col{＆p1};array k1{＆p1};array k2{＆p1};do i=1 to ＆p1;k1{i}=b{i}-col{i};k2{i}=-b{i}-col{i};if_n_=1 then k1{i}=k1{i}*-1;if_n_=1 then k2{i}=k2{i}*-1;end;k21=k21*-1;run;

data KE;/*合并KE1、KE2得KE，即为方阵H12*/

set KE1 KE2;

run;

proc transpose data=ke out=ke;/*对方阵H12进行适当的转换，去掉全1列*/

run;

data ke(drop=c_NAME_);set ke;c=sum(of col1-col＆n);if c= ＆n then delete;

run;

proc transpose data=ke out=ke(drop=_NAME_);

run;

data zj(drop=i);/*数据集zj即为所求*/

set ke;array col{＆k};do i=1 to ＆k;if col{i}=-1 then col{i}=2;end;run;

proc sort;by col1 col2 col3;

run;

在SAS程序中只需修改宏变量n(试验次数)，就可以构造其他试验次数但满足GF(p)的一个元根为2的N≠2s且N=2(p+1)(p为素数且p≡1(mod4))型2水平正交表，如 L26(225)、L36(235)、L60(259)等。当有限域的元根不包含2时，则需在修改宏变量n的基础上，再修改宏变量yg(元根)即可。

3．Lt2(tm)型正交表的SAS实现

为了SAS操作的简便，采用有限域的一个元根法建立通用的n阶正交拉丁方完全组，并以L25(56)为例介绍SAS过程。其中，SAS生成的数据集LT即为所求，结果见表3，程序与注解如下。

表2 L12(211)正交设计表

%let t=5;/*宏变量t即L_(t2)(tm)中的t值*/

%let t1=%eval(＆t+1);

%let fz=%eval(＆t－1);/*宏变量fz表示正交拉丁方完全组方阵的个数，其值等于t-1*/

%macro iml;/*结合原理，运用宏程序和proc iml过程构造四个方阵*/

%do g=1%to＆fz;

proc iml;a=j(＆t，＆t);do i=1 to ＆t;

a［1，i］=i;/* 创建每个方阵的第一行*/

end;x=＆t*2-1;do i=2 to＆t;/*依据原理创建方阵的其他行*/

do j=1 to＆t;do k=3 to x;

m=i-1;l=j+1;

if i+j=k ＆ j^= ＆t then a［i，j］=a［m，l］+ ＆g-1;

if a［i，j］=0 then a［i，j］= ＆t;

if a［i，j］＞ ＆t then a［i，j］=mod(a［i，j］，＆t);

a［i，＆t］=A［1，+］-A［i，+］+a［i，＆t］;end;end;end;create c＆g from a;append from a;close c＆g;quit;

%end;%mend iml;%iml;

%macro cl;/*调用宏程序将proc iml创建的每个方阵均转换成列*/

%do k=1%to ＆fz;proc transpose data=C＆k．out=CC＆k．(drop=_NAME_);var_all_;run;%do i=1%to ＆t;data CC＆k．＆i．(keep=col＆i rename=(col＆i=col1));set CC＆k．;run;%end;data CC＆k．(rename=(col1=C＆k．));set%do i=1%to ＆t;CC＆k．＆i．

%end;;run;%end;%mend cl;%cl;

data CC＆t．;/*创建图1中的基本列——第一列和第二列*/

do BASE1=1 to＆t;do BASE2=1 to＆t;output;end;end;

run;

%macro hb;/*将基本列的数据集和方阵转换成列的各个数据集合并成一个数据集LT，即为所求的正交表*/

data LT;length base1 base2 8．;merge%do i=1%to ＆t．;CC＆i．%end;;

run;

%mend hb;

%hb;

表3 L25(56)正交设计表

在程序中只需修改宏变量t的值即可得到t为素数的Lt2(tm)类型正交表。但当t不为素数时，基于生成Lt2(tm)类型正交表的正交拉丁方结构不同，其SAS程序更为复杂，这里暂不介绍。

4.混合正交表的SAS实现

本文以混合正交表L16(43×26)(即L16(4k×2m)型混合正交表)为例，介绍如何通过水平数相等的正交表L16(215)通过“并列法”进行构造，结果见表4，SAS程序与注解如下。%let K4=3;/*宏变量K4表示水平数为4的因素个数*/

data hh1(drop=i col1 col2 col3 col4);/*运用“并列法”将L16(215)进行改造*/

length col23 col59 col611 col810 col712 6．;set zj2;/*调用哈达玛矩阵法中生成的数据集zj2，即L16(215)*/

col23=col3*(col2=1)+(col2+col3)*(col2=2);

col59=col9*(＆K4＞ =2 and col5=1)+(col5+col9)*(＆K4＞ =2 and col5=2);

if col59^=0 then do;col5=0;col9=0;col13=0;end;col611=col11*(＆K4＞ =3 and col6=1)+(col6+col11)*(＆K4＞ =3 and col6=2);

if col611^=0 then do;col6=0;col11=0;col16=0;end;col810=col10*(＆K4＞ =4 and col8=1)+(col8+col10)*(＆K4＞ =4 and col8=2);

if col810^=0 then do;col8=0;col10=0;col15=0;end;col712=col12*(＆K4=5 and col7=1)+(col7+col12)*(＆K4=5 and col7=2);

if col712^=0 then do;col7=0;col12=0;col14=0;end;

run;

proc transpose data=hh1 out=hh2;var_all_;

run;

data hh1;set hh2;if col1=0 then delete;

run;

proc transpose data=hh1 out=hh2;

var_all_;

run;

data hhzj(drop=_NAME__LABEL_);

set hh2;

if_NAME_=“_NAME_”then delete;

run;

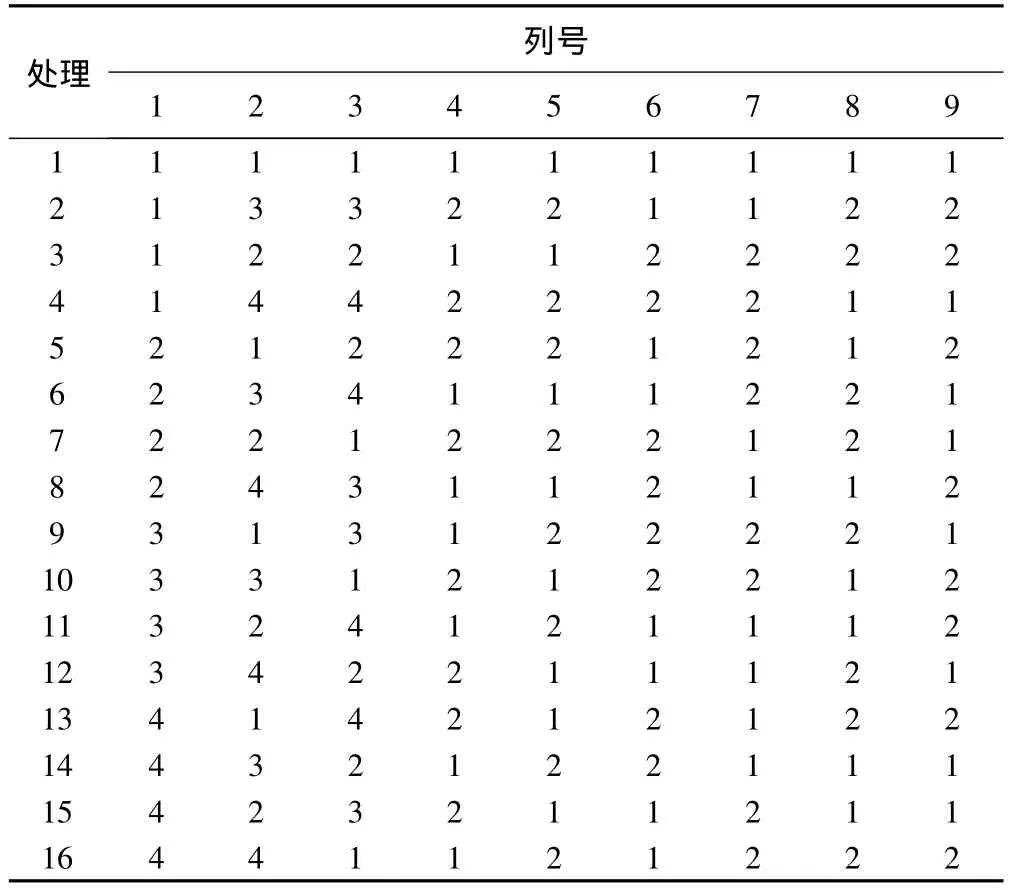
表4 L 16(43×26)正交设计表

上述程序中混合正交表L16(4k×2m)，当K不同时，程序中只需修改宏变量K4即可，K4的取值为整数，范围是〔1，5〕。不同的试验次数，水平数为素数幂的混合正交表也可参照同样的原理及方法生成。

结 论

构造正交表的方法繁多，但不同类型的正交表的构造原理与方法往往不同。本文根据不同类型正交表的构造原理，完成了四种类型正交表SAS通用构造程序。这样，可以解决正交试验设计中获得相应正交表的困扰，方便实用，具有较强的应用价值。

1．Zhang YS，Li WG，Mao SS，et al．Orthogonal arrays obtained by generalized difference matrices with g levels．SCIENCE CHINA，2011，54:133-143．

2．Ma CX，Fang KT，Erkki Liski．A new approach in constructing orthogonal and nearly orthogonal arrays．Metrika，2000，50:255-268．

3．Aloke Dey，Midha CK．Construction of some asymmetrical orthogonal arrays．Statistics ＆ Probability Letters，1996，28:211-217．

4．Liu ZW．A survey of orthogonal arrays of strength two．Acta Mathematicae Applicatae Sinica，1995:308-317．

5．Man VM．Nguyen．Some new constructions of strength 3 mixed orthogonal arrays．Journal of Statistical Planning and Inference，2008，138:220-233．

6．Zhang YS，Pang SQ，Wang YP．Orthogonal arrays obtained by generalized Hadamard product．Discrete Mathematics，2001，238:151-170．

7．Sloane NJA，Hedayat AS，John Stufken．Orthogonal arrays:theory and applications．Springer-verlag New York Inc，1999．

8．杨子胥．正交表的构造．山东:山东人民出版社，1978．