不等高双肢薄壁墩对大跨连续刚构静力影响＊

（昆明理工大学建筑工程学院 昆明 650500）

目前对大跨连续刚构桥桥墩的研究主要集中在桥墩类型的选取［1］、桥墩刚度的计算［2－4］、桥墩尺寸的优化［5－9］、不同桥墩形式连续刚构桥的地震响应分析［10］等．连续刚构桥梁为适应温度变化、混凝土收缩徐变和地震力产生的纵向水平变形，下部桥墩通常设计为具有较小抗推刚度的双肢薄壁墩．同时为使主墩墩顶具有相同的变形能力，大跨连续刚构桥的主墩多采用等高设计．但当受到桥位处地形的限制，采用主墩的等高设计可能会造成桥梁施工难度较大、经济性不合理等，甚至无法实现，而采用不同截面的不等高桥墩会增加施工的难度和费用．因此本文研究具有相同截面的不等高桥墩对桥梁的静力影响具有一定的实际工程意义．

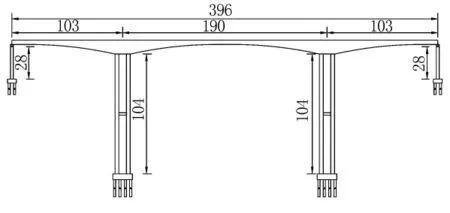
图1 某特大桥立面布置图（单位：m）

1 工程背景

分析以某在建公路特大桥为例，该桥主桥为3跨变截面预应力混凝土连续刚构，桥跨布置为103m＋190m＋103m，见图1．

桥梁上部主梁截面为单箱单室箱型截面，箱梁顶板宽12m，底板宽6．5m；下部2主墩为高度与截面均相同的双肢薄壁墩，墩高104m，双肢薄壁截面肢中心距10．5m，纵桥向单肢宽3．5m，壁厚0．6m，横桥向单肢宽8．5m，壁厚1．0m，墩身采用C50混凝土．

2 计算与分析

2.1 有限元模型的建立

以原设计桥梁所对应的有限元模型作为墩高比为1．0的计算模型．为考虑不同墩高比对连续刚构的静力影响，假定桥梁下部某一桥墩的高度固定不变，而将其余墩高取不同的值，形成不同的墩高比．除墩高比为1．0的模型外，其余模型的墩高比拟取值为0．5，0．6，0．7，0．8，0．9．

变高度桥墩的高度根据确定的墩高比计算见表1．

表1 变化桥墩高度表

模型中横系梁的设置为，对于墩高比分比为0．5，0．6，0．7，0．8，0．9，1．0的模型，分别在桥墩中部设置一道横系梁．所有模型中桥墩横系梁的尺寸均相同．

根据文献［4］中被动位移阶段桥墩抗推刚度的计算方法，墩定转动自由与墩顶受到严格约束时，桥墩抗推刚度的计算式为

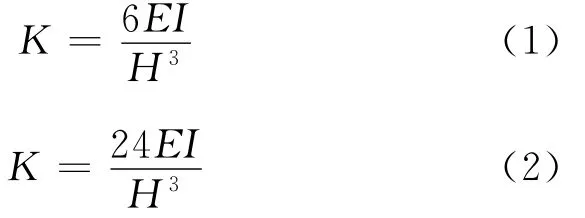
式中：K为双肢薄壁墩的抗推刚度；E为墩的弹性模量；I为墩截面的惯性矩；H为桥墩的高度．

由式（1）与式（2）可见，无论主梁对桥墩墩顶转动约束强弱，在桥墩的截面尺寸相同时，桥墩的抗推刚度与桥墩高度的三次方成反比关系，据此计算变高度桥墩与固定高度桥墩的抗推刚度比见表2．

表2 桥墩抗推刚度比

2.2 计算结果

根据上述建立的具有不同墩高比桥梁的有限元计算模型进行计算．按文献［11］所述，考虑承载能力极限状态时，荷载的最不利组合取为：1．2×恒荷载＋1．2×预应力次效应＋1．0×混凝土收缩作用＋1．0×混凝土徐变作用＋1．4×汽车荷载＋0．98×人群荷载＋0．98×温度作用．分别统计各模型的边跨正弯矩、中跨跨中弯矩、边跨根部弯矩、中跨根部弯矩、墩顶弯矩、墩底弯矩、结构竖向基频、主梁支座处水平位移见表3～7．

表3 高墩侧组合弯矩

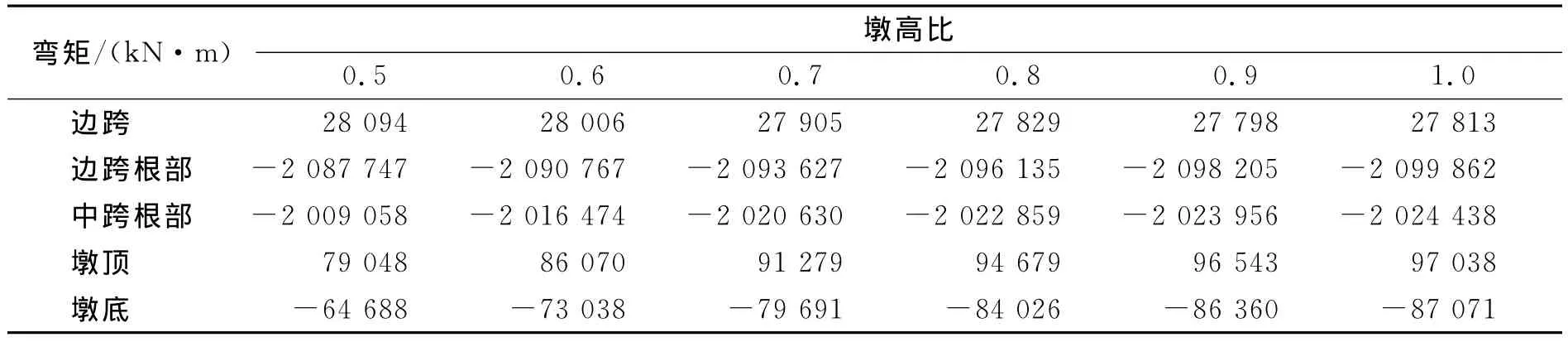
表4 低墩侧组合弯矩

表5 跨中组合弯矩

表6 桥梁结构竖向基频

表7 主梁支座处水平位移（绝对值）

2.3 计算结果分析

根据表3、表4的计算结果，在某一墩高比时，桥梁的边跨正弯矩、边跨根部弯矩、中跨根部弯矩、墩顶弯矩、墩底弯矩、支座处位移的绝对值在高墩侧与低墩侧的差值百分比（差值与较小值百分比）见表8．

根据表3～7的计算结果，分别作边跨正弯矩、边跨根部弯矩、中跨根部弯矩、墩顶弯矩、墩底弯矩、中跨跨中弯矩、结构竖向基频、主梁支座处水平位移的绝对值与墩高比的关系见图2～9．

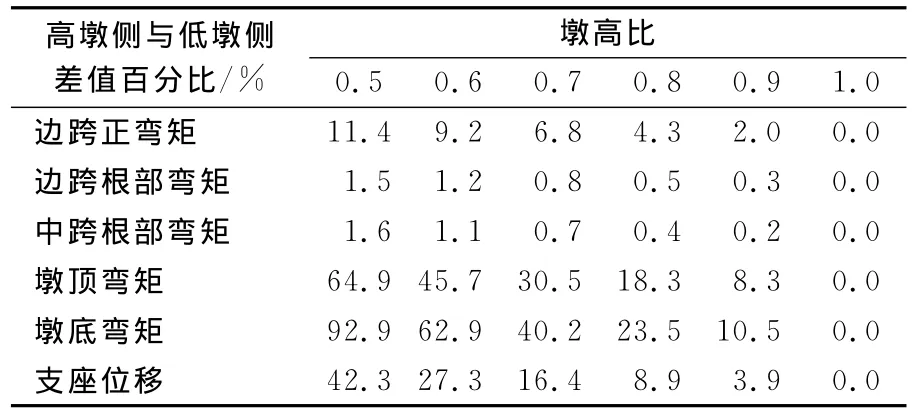
表8 各参数的差值百分比

图2 边跨正弯矩－墩高比关系图

图3 边跨根部弯矩－墩高比关系图

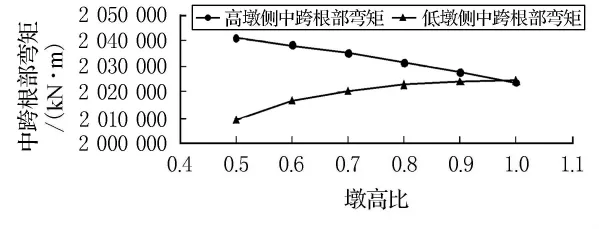
图4 中跨根部弯矩－墩高比关系图

图5 墩顶弯矩－墩高比关系图

图6 墩底弯矩－墩高比关系图

图7 跨中弯矩－墩高比关系图

图8 竖向基频－墩高比关系图

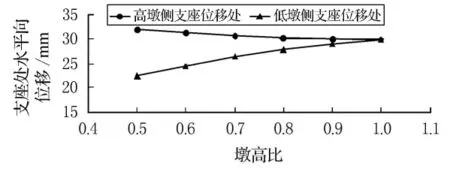
图9 支座处水平位移－墩高比关系图

根据表3及图2～6的分析，当桥墩的墩高比从0．5变化至1．0时，高墩侧边跨正弯矩值相应增大，最大变化幅度为10．32%；而高墩侧边跨根部弯矩、中跨根部弯矩、墩顶弯矩、墩底弯矩绝对值趋于减小，最大变化幅度分别为0．88%，0．85%，25．52%，30．25%．

根据表4及图2～6的分析，当桥墩的墩高比从0．5变化至1．0时，低墩侧边跨正弯矩值相应减小，最大变化幅度为1．0%；而低墩侧的边跨根部弯矩、中跨根部弯矩、墩顶弯矩、墩底弯矩绝对值则趋于增大，最大变化幅度值分别为0．58%，0．77%，22．76%，34．6% ．

由表5计算结果及图7的分析表明，桥墩墩高比的变化对桥梁跨中弯矩影响甚小．当桥墩的墩高比从0．5变化至1．0时，其值变化仅为0．602%．

根据表6计算结果及图8的分析，可以得出当桥墩的墩高比增大时，桥梁结构的竖向基频随之减小，最大减小幅度为8．83%，但变化幅度远小于桥墩墩高的变化幅度．若根据文献［11］桥梁冲击系数的取值方法，当f＜1．5Hz时，冲击系数均取0．05，则墩高比对本桥车辆荷载冲击作用的影响可忽略不计．

根据对表7及图9的分析表明，当墩高比增大时，高墩侧支座位移绝对值趋于较小，低墩侧的支座位移绝对值则趋于增大．当墩高比由0．5变化至0．8时，同一桥梁两侧支座处位移差值较大．

由表8的分析，在墩高比相同时，高低墩侧对应的边跨正弯矩、边跨根部弯矩、中跨根部弯矩、墩顶弯矩、墩底弯矩、支座位移绝对值的最大差值百分比分别为11．4%，1．5%，1．6%，64．9%，92．9%，42．3%．且差值随着墩高比的增大而逐渐减小．

3 结 论

1）墩高比对桥梁上部结构的静力影响相对较小，当墩高比由0．5变化至1．0时，除边跨正弯矩外，其余的影响幅度均小于5%；在墩高比相同时，除边跨正弯矩外，其余影响幅度均小于5%．

2）墩高比对桥墩本身的静力影响较大，当墩高比由0．5变化至1．0时，墩顶弯矩最大变化幅度为25．52%，墩底弯矩最大变化幅度为34．6%；在墩高比相同时，2墩墩顶弯矩、墩底弯矩最大差值的百分比分别为64．88%，92．9%．

3）在连续刚构桥梁的设计中，当受地形限制而不能采用等高主墩时，可采用具有相同截面的不等高双肢薄墩．但上部需在主梁高墩侧边跨加强底板抗弯预应力束，并在主桥两侧设置不同类型的伸缩缝；下部桥墩的配筋应满足桥梁的受力要求．

［1］王钧利，贺拴海．大跨连续刚构桥主墩类型及设计尺寸优化［C］／／中国公路学会桥梁与结构分会2006年全国桥梁学术会议论文集，北京：人民交通出版社，2006：161－166．

［2］徐君兰，顾安邦．连续刚构桥主墩刚度合理性的探讨［J］．公路交通科技，2005，22（2）：59－62．

［3］王钧利，贺拴海．大跨径连续刚构桥主墩的合理刚度分析［J］．武汉理工大学学报：交通科学与工程版，2006，30（4）：603－606．

［4］张永水，曹淑上．连续刚构桥薄壁墩抗推刚度计算方法研究［J］．中外公路，2006，26（3）：144－147．

［5］张会杰．基于可靠度的连续刚构双肢薄壁墩优化设计［D］．成都：西南交通大学，2007．

［6］李 杰，徐 岳，郑凯锋．连续刚构桥双薄壁墩参数优化研究［J］．公路，2004（4）：73－78．

［7］谭平荣，王 麒．连续刚构双片墩尺寸优化设计［J］．公路，2007（8）：17－20．

［8］韩 艳，陈政清，李开言．在ANSYS中实现双肢薄壁墩桥墩参数优化设计的方法［J］．铁道科学与工程学报，2005，2（6）：15－18．

［9］董晓梅．高墩大跨径连续刚构桥墩身稳定性分析及参数优化［D］．西安：长安大学，2007．

［10］周勇军，贺拴海．连续刚构桥单双薄壁墩地震响应的对比分析［J］．中外公路，2007，27（3）：114－117．

［11］中交公路规划设计院．JTG D60－2004公路桥涵设计通用规范［S］．北京：人民交通出版社，2004．