任意形状三元阵水下目标被动定位研究＊

（海军工程大学电子工程学院 武汉 430033）

0 引 言

基于时延的三元阵被动定位技术是一种对目标进行被动定位的经典方法．然而，传统的三元阵通常为等间距的线列阵，在实际的安装布放过程中存在诸多不便．为了对此进行改进，文献［4］推导了不等间距非直线三元阵的定位公式，文献［5］推导了任意形状三元阵平面声被动定位公式．但是这些推导建立在目标声源与三元阵在同一平面的前提下，这就使得三元阵只能测定目标的二维方位信息，获取目标的三维状态信息则必须增加传感器数量，这又增加了阵列的复杂度及成本．

矢量水听器是一种新型水声传感器，它与传统的声压水听器的最大区别在于：它不仅可以给出声压信息，而且可以提供振速信息［6］．利用矢量水听器的这种多信息输出，可以确定目标的方位．但是，单个矢量水听器对于声源俯仰角的测量误差是很大的，而且不能给出目标的距离信息．矢量水听器阵列固然可以解决这些问题，然而，矢量水听器的制造成本高昂［7］，用大量矢量水听器组成阵列在工程实现上会造成成本大幅提高，存在一定的困难．

针对目前存在的这些问题，文中提出了一种由矢量水听器和声压水听器组成的任意形状三元阵，对定位公式进行了推导，并通过实验验证了其正确性和有效性．

1 定位原理

定位系统利用1个矢量水听器和2个声压水听器组成任意形状三元阵，对水下目标进行定位，其示意图见图1．不失一般性，对于任意给定的一个三元阵，可建立如下坐标系．选定矢量水听器H1为坐标原点，H1，H2，H3确定的平面为yoz平面；H1与声压水听器H2的连线作为y轴；另一声压水听器H3在该平面任意位置．S为声源，θ为声源的方位角；φ为声源的俯仰角；r1，r2，r3分别为声源到H1，H2，H3的距离．

图1 三阵元定位系统示意图

1.1 方位角解算

矢量水听器可以共点、同步、独立地测量声场空间某点处的声压p（r，t）和质点振速v（r，t）的3个正交分量vx（r，t），vy（r，t），vz（r，t）．可利用频域复声强对声源方位进行估计，这种方法能够抑制同性非相干干扰．复声强定义为［8］

式中：p（r，ω），v（r，ω）分别为p（r，t），v（r，t）的傅里叶变换；＊表示复共轭．则声源的水平方位角θ为

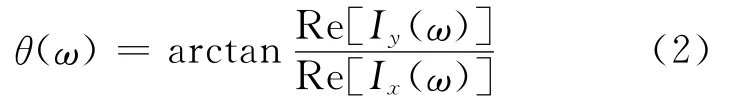
式中：Ix（ω）和Iy（ω）分别为坐标轴x，y方向上的复声强；Re［］为取实部运算．

1.2 俯仰角和距离解算

下面对声源的俯仰角和距离进行公式推导．在图1中，已知 H1，H2，H3的坐标分别为（0，0，0），（0，y2，0），（0，y3，z3）．设点声源 的坐标为（xs，ys，zs），传播速度为c，声源到水听器 H1，H2和H1，H3的时延分别为τ12和τ12，则它们的距离差d12和d13分别为

我们在一所有着百年历史的顶尖私立高中，见到了这位厉害的马克老师。马克老师自1975年耶鲁博士毕业后，就在此教学，已经有40多年的教龄了。多年的教学生涯让马克老师对历史教学有自己的见解和认识，他为我们呈现的，是另一种形式的教学。

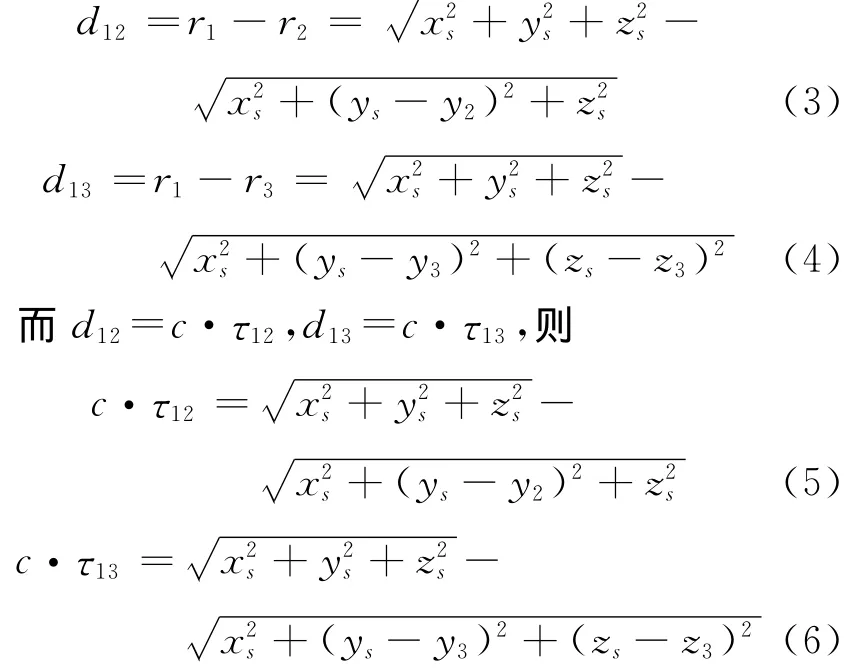
式中：时延τ12和τ13可以通过广义互相关法［9］获得，又根据1．1的方位角解算θ可以获取，有

联合方程式（5）～（7）求解即可得到声源S的三维坐标（xs，ys，zs），则声源的距离r和俯仰角φ分别为

需要指出的是，方程组（5）～（7）计算可能会得出2组解，其中一解为增解，可由物理事实判断排除．

2 误差分析

通过以上分析可以看出，影响定位结果的几个因素包括：声速测量误差、时延估计误差、方位角估计误差等．下面对这些造成误差的因素进行分析．

声音在水中远距离传播时，受到水层深度、盐度、温度等影响．其在传播路径上各点的声速值会发生变化，如果采用平均速度来计算会带来误差．实际应用中，常采用经验公式或者根据射线声学的理论对声速值进行修正，经修正后的所引起的测距误差一般可控制在0．5%左右［10］，对测量结果影响不大．

由时延估计误差引起的测距误差和俯仰角误差分析如下：

由于相互独立正态分布变量的线性和仍为正态分布，其方差为各变量方差的和，所以测量距离的方差为

根据文献［11］，基于声强的方位估计的CRB为

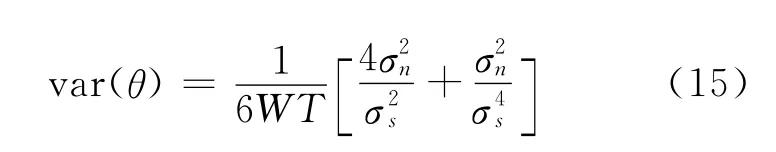
3 实验结果分析

为了验证定位系统的性能和算法的有效性，在消声水池进行了实验，实验过程见图2．系统主要组成有：信号发生器采用Tektronix AFG3022B型任意波形函数／函数发生器；水声换能器采用SKS－8／16声信号发射换能器；矢量水听器采用HS／20－1．5K同振式三维水听器；声压水听器采用SMH－102柱形水听器；数据采集器采用UDAQ20016型多通道同步并行数据采集器；前置放大器采用一款可以进行20倍电压放大的前放电路，用于放大来自水听器的微弱电信号，使其达到数据采集器所要求的电压值，实际使用时加上密闭设备保证水密性；功率放大器采用JYH－200A功率放大器．实验中采样率为200 kHz，观测时间为20s，声传播速度取1 480m／s．

图2 消声水池实验场景

第1次实验在不加环境噪声的条件下进行，测试算法的正确性．采用的声源为事先采集好的行船噪声信号，先后在2个位置对声源进行定位，每个位置测试3次取均值，其中，声源位置的理论值通过几何计算获得．结果见表1．

表1 无噪声情况下定位结果

从定位结果可以看出，在没有噪声干扰的条件下，定位算法的距离测量误差不超过0．2m，相对误差控制在3%以内．角度测量误差在1°左右，相对误差在10%左右，说明提出的算法是正确有效的．

在实际环境中进行目标定位，必然会受到环境噪声的干扰，为了检验该算法在背景噪声影响下的定位性能，第2次实验对采集的行船噪声信号分别加入了湖泊背景噪声和仿真的海洋噪声，模拟测试在湖泊和海洋等真实环境下算法的性能．信噪比设置为0dB，测试3次取均值．结果见表2．

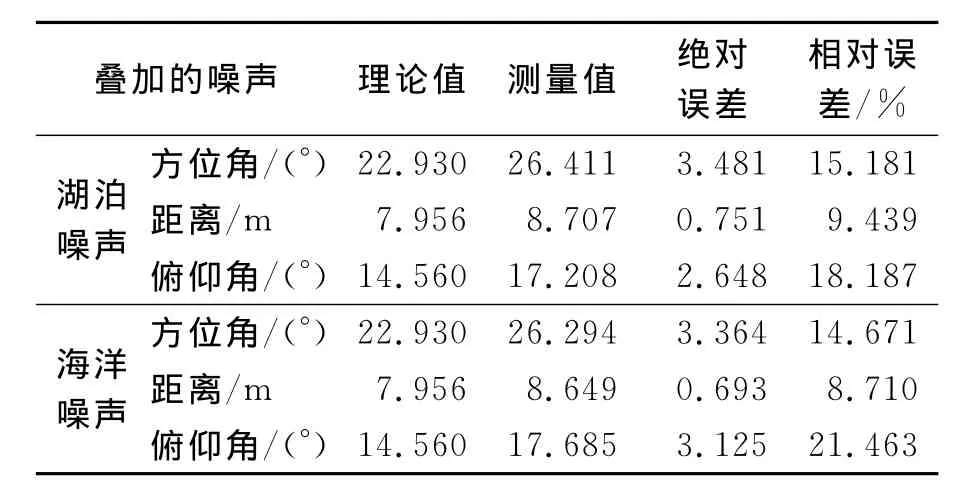
表2 不同噪声情况下定位结果

实验结果显示，在环境噪声干扰下，算法的定位精度相对于之前无噪声下的测试出现了一定程度的下降，其中，距离误差在1m以内，角度误差不超过4°，算法仍然是有效的．

总之，2次实验结果表明：新算法实现了用任意形状三元阵对声源进行三维定位的目的，体现出了一定的抗噪性．

4 结束语

本文提出的结合矢量水听器和声压水听器的任意形状三元阵定位方法，在没有大幅提高设备成本和增加阵元数量的前提下，实现了对声源目标三维位置信息的获取，降低了实际操作中对阵元位置摆放的要求，扩展了三元阵的使用范围，具有广泛的应用前景．通过改进时延估计算法，进一步提高定位精度，是下一步需要研究的问题．

［1］CARTER G C．Passive sonar signal processing［C］／／Proc．of NATO ASI on Underwater Acoustics and Signal Processing，1980：499－508．

［2］周 伟，门丽杰，梅继丹，等．浅海三元阵近程被动定位实验研究［J］．哈尔滨工程大学学报，2009，30（5）：547－551．

［3］曲 毅，刘 忠，周 伟，等．基于等间隔线阵的水下三维目标跟踪算法［J］．武汉理工大学学报：交通科学与工程版，2007，31（6）：955－957．

［4］魏丽萍，吴国清，陈 庚，等．水下不等间距非直线目标定位海上实验［J］．声学技术，2008，27（5）：474－475．

［5］张卫平，王伟策．任意形状三阵元平面声被动目标定位分析［J］．探测与控制学报，2003，25（3）：54－57．

［6］孙贵青，李启虎．声矢量传感器信号处理［J］．声学学报，2004，29（6）：491－498．

［7］王千喜，李 潺，蔡惠智，等．一种矢量水听器基阵模拟器的设计［J］．应用声学，2006，25（3）：173－179．

［8］孙贵青，杨德森，张 林，等．矢量水听器在水下目标低频辐射噪声测量中的应用［J］．哈尔滨工程大学学报，2001，22（5）：5－9，19．

［9］崔纬纬，曹志刚，魏建强．声源定位中的时延估计技术［J］．数据采集与处理，2007，22（1）：90－99．

［10］彭鹏菲，刘 忠，陈显尧．柔性三元垂直线阵在水下目标被动定位中的应用［J］．探测与控制学报，2008，30（2）：27－30，34．

［11］孙贵青，杨德森，张揽月，等．基于矢量水听器的最大似然比检测和最大似然方位估计［J］．声学学报，2003，28（1）：66－72．