改进的BP神经网络预测模型及其应用

（武汉东湖学院管理学院 武汉 430212）

随着计算机计算能力提高的进展，越来越多的研究者把神经网络和支持向量机等方法应用于各类预测问题，人工智能预测方法用于预测问题的研究优势更加明显，并取得了有效的成果［1－3］．时间滞后的周期性网络（time lagged recurrent networks，TLRN）运用于水量预测模型研究［4－5］，不同的研究结果表明TLRN模型结果优于其他的统计模型．相对于传统的预测方法如灰色预测、线性回归法、指数平滑法、季节趋势预测等方法，人工智能预测方法建模简捷且预测精度和效率更高［6］．本文将利用引入加入动量因子和自适应学习速率的方法对BP神经网络预测方法进行改进，从而有效解决基于BP学习方法易于陷入局部极值和收敛速度慢的问题．将改进后的人工神经网络预测方法应用于市场需求预测问题研究，并结合某汽车制造企业的市场实际数据，进行实证研究．

1 改进的BP神经网络模型

人工神经网络（artificial neural network，ANN）是一种用大量处理单元广泛连接组成的人工网络，用来模拟人的大脑神经系统的结构和功能，是人脑的某种抽象和简化，而不是完全的真实描写［7］．BP神经网络已经成功地用于材料数据试验处理、摩擦磨损行为分析、图像处理、模式识别、自动控制等领域［8］．李彦斌等引入峰值识别理论改进BP神经网络预测模型（SIBP）解决传统人工智能预测算法在对预测问题峰值变化处理问题上的不足，提出一种具有峰值识别能力、全局学习能力更强的人工智能预测模型，以有效解决基于BP学习方法易于陷入局部极值的问题［9］．本文提出的改进的BP神经网络是在反向传播法的基础上，在每一个权值的变化上加上一项正比于前次权值变化量的值，再依据反向传播产生新的权值变化．包含附加动量因子的权值调节公式为

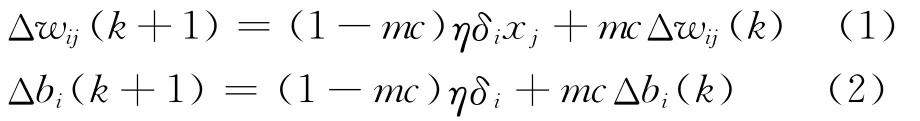
式中：i为隐含层数；j为隐含层节点数；k为训练次数；Δw为权值的增量；η为学习速率；δ为网络学习误差；x为网络输入；mc为动量因子．

在网络训练中采用自动调整学习速率法（即自适应学习速率法）来解决这个问题．自适应学习速率法的的核心思想是网络训练时，检查权值的修正值是否降低了误差函数，说明学习速率值小了，则对其增加一个量；否则，减小学习速率的值．自适应学习速率的调整公式为

式中：erf为误差函数；yi为学习样本的输出值；为网络训练后yi的实际输出值；n为学习样本的个数．

2 实证分析

本文以某汽车制造企业在过去12个月汽车的销售量进行预测分析，销售部经过长期与产品销售市场接触，通过对大量销售数据和市场情况的分析，总结出影响汽车市场销售主要因素有：价格、品牌知名度、营销服务水平、地区经济状况和政策，其中，价格则采用某一地区某种品牌的产品与其他品牌的销售价格差来表示同比价格优势，品牌知名度采用广告费用来反映，服务水平以营销服务水平反映，政策属于不可控因素．因此，影响产品销售的主要因素归结为：同比价格优势，广告费用和服务水平3个指标．具体数据见表1．以1～12个月实际数据为样本数据，利用1～10个月的数据进行网络训练，利用11～12个月的数据进行数据测验．实现工具为Matlab11b．0．

表1 某产品的销售量、销售价格、广告费用、服务水平等相关的数据

2.1 基于时间序列的销售额预测

基于时间序列的预测方法是指预测一段时间内销售量变化的大致趋势，即销售量随时间序列的变动情况．汽车销售量是一组按时间顺序排列的数据序列，即时间序列，因此可采用基于时间序列的预测方法．设定预测算法结束条件为误差达到0．000 1，迭代次数为2 000次，预测结果见表2、图1和图2．

表2 学习样本与测试样本结果对照表

图1 市场的汽车销售额预测结果与真实汽车销售额对比

图2 改进的BP网络训练过程曲线

2.2 基于影响因素分析的销售额预测

根据以上分析，影响汽车销售的主要因素有3个，则输入层神经元个数为3，即m＝3，则输入函数为：X＝（x1，x2，x3）．预测目标为销售量，即只有一个，则输出层神经元个数为1，即n＝1．有一个粗略的估计方法，隐含层神经元数目约为输入层神经元个数的2倍左右，即l＝2m，则BP神经预测模型为：Y＝f（X）＝f（x1，x2，x3）．模型含有3个输入神经元，隐层有5个神经元，1个输出神经元，具体如图3所示．采用Matlab2011b中的Simulink工具对图3建模，提高了预测操作的便捷性和智能化，则对应的Simulink模型和输入层和隐层的权值分配结构模型见图4和图5．

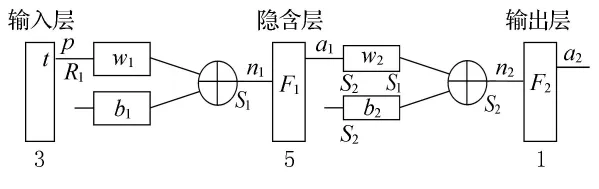
图3 具有一个隐层的BP神经网络示意图

图4 神经网络BP算法的Simulink仿真模型

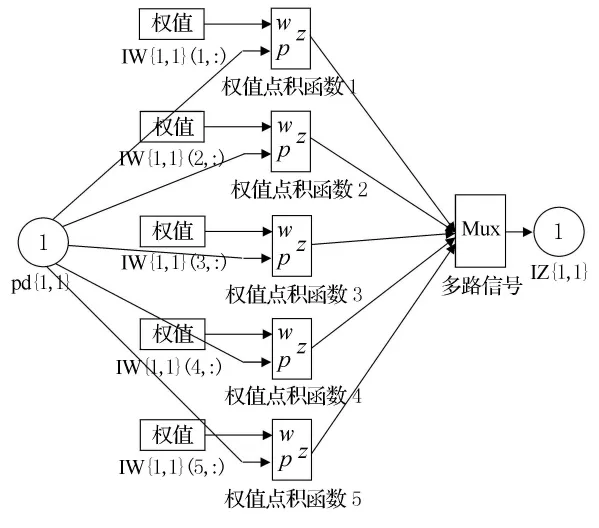
图5 神经网络BP算法输入层－隐层的权值分配结构模型

用训练好的网络，输入表1中的后两组数据进行需求预测，输出指标预测数据见图6和图7．

图6 第11月份预测结果

图7 第12月份预测结果

11月份的需求预测为385 4辆，实际销售量为366 2辆，预测误差为5．243 0%．

12月份的需求预测为445 2辆，实际销售量为429 2辆，预测误差为3．727 8%．

预测的结果见表3和图8．

3 仿真结果分析

本文提出的预测模型是可用的：（1）由预测结果数据可以看出，预测结果非常接近于真实的销售结果．由图1和图2可以看出，引入附加动量法和自适应学习速率法后，采用本文提出的基于时间序列的预测模型预测曲线非常接近于真实的销售量曲线，11月份的销售量波动稍大，误差为8．741 1%，12月相对平稳，误差为5．005 7%，预测精度非常高，训练时间也比较短．由表3和图8可以看出，基于影响因素分析的销售额预测模型预测精度高于基于时间序列的预测模型，11月份和12月份的误差分别为5．243 0%和3．727 8%．说明本文提出的预测模型能够更好地适应汽车市场环境下短期销售量预测的需要；（2）此预测模型能够很好地适应市场的变化．当市场发生变化时，可以通过改变参数重新训练网络，实现市场需求预测的动态化．比如广告费用指标不是影响销售额的主要因素了，产品质量因素越来越重要了，则产品质量可取代广告费用或增加这个指标；（3）把神经网络方法应用于现代销售预测的定量研究具有很好的现实意义，通过对这些指标的预测，不仅仅获得了指标的数据，更重要的是可以运用这些数据，并结合实际情况，对企业决策方案进行分析，为企业的战略决策提供定量的决策依据．

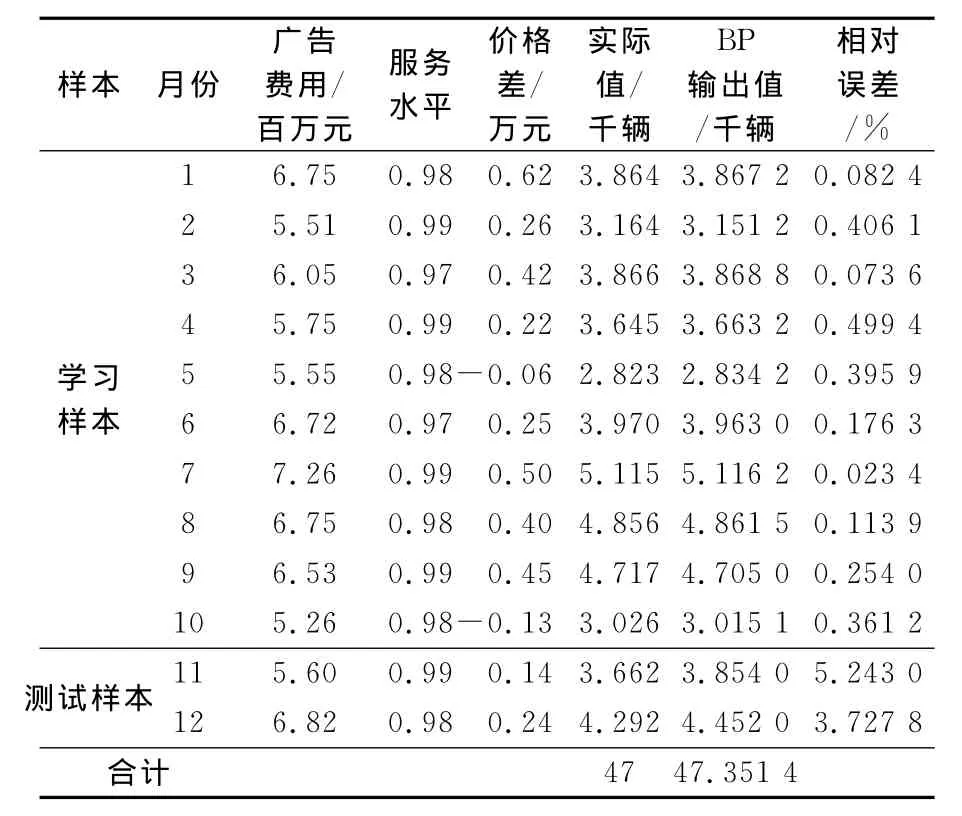
表3 BP网络学习与预测结果对照表

图8 改进的BP网络训练过程曲线

4 结束语

本文在传统BP神经网络算法的基础上，引入附加动量法和自适应学习速率法改进BP神经网络预测模型，解决了网络具有易陷入局部极小、收敛速度慢的缺陷，能有效提高算法的精度，提高了网络学习能力．分别采用基于时间序列和基于因素分析两种预测模型，对所提出的改进预测方法进行实证分析．实证分析结果表明，采用改进的BP神经网络算法预测精度较高，且能较好地收敛到最优值．

［1］ZHU Ying．Study on the model of demand forecasting based on artificial neural network［C］／／The 9th International Symposium on Distributed Computing and Applications to Business，Engineering and Science．Hong Kong，2010：382－386．

［2］AL－BULUSHI N I，KING P R，BLUNT M J．Kraaijveld artificial neural networks workflow and its application in the petroleum industry［J］．Neural Comput ＆ Applic，2012，21：409－421．

［3］CAN B，HEAVEY C．A comparison of genetic programming and artificial neural networks in metamodeling of discrete－event simulation models［J］．Computers ＆ Operations Research，2012，39：424－436．

［4］SATTARIA M T，YUREKLI K，PAL M．Performance evaluation of artificial neural network approaches in forecasting reservoir inflow［J］．Applied Mathematical Modelling，2012，36：2649－2657．

［5］JEONG K S，KIMB D K，JUNGC J M，et al．Nonlinear autoregressive modelling by temporal recurrent neural networks for the prediction of freshwater phytoplankton dynamics［J］．Ecol．Model，2008，211：292－300．

［6］CONEJO A J，PLAZAS M A，ESPINOLA R，et al．Day－ahead electricity price forecasting using the wavelet transform and ARIMA modesl［J］．IEEE Trans Power System，2005，20（2）：1035－1042．

［7］彭祖赠．数学模型与建模方法［M］．大连：大连海事大学出版社，1997．

［8］VELTEN K，REINICKE R，FRIEDRICH K．Wearvolume predictionwith artificialneuralnetworks［J］．Tribology International，2000，33：731．

［9］李彦斌，李存斌，宋晓华．改进的人工智能神经网络预测模型及其应用［J］．中南大学学报：自然科学版，2008，39（5）：1054－1059．