结构－声辐射功率灵敏性分析与应用研究

（上海交通大学船舶海洋与建筑工程学院 上海 200240）

0 引 言

在中低频段，有限元法和边界元法广泛应用于结构－声辐射问题．结构－声辐射灵敏度是结构声学指标如声压、声强及声辐射功率等参数随结构设计参数的变化率．灵敏度信息可为结构－声辐射优化提供参考、有效改善结构声学特性．Kim等［1］用有限元法分析了轿车内声压灵敏性问题．Wang等［2］根据声压灵敏度信息进行箱形结构外部声压的优化．Cheng等［3］对声辐射功率的频率灵敏度开展了研究．Marburg等［4－5］通过改变结构模态来优化壳体声辐射功率，并用于汽车底板的声设计．Li等［6］用遗传算法进行结构的质量分布优化，以减少圆柱壳结构声辐射．陈美霞等［7］采用有限元和边界元方法分析平板在空气和水中的振动和声辐射，对比流体特性对声辐射特性的影响．丁少春等［8］运用功率流法对舰艇进行声辐射分析，通过数值对比隔振装置性能参数对舰艇声辐射功率的影响，提出控制舰艇噪声的基本原则．孙淦云等［9］开展了具有耦合系统的密闭空腔的动力响应分析和灵敏度计算，计算固有频率和声压级响应对结构尺寸的灵敏度．张军等［10］结合有限元法和边界元法计算声学灵敏度，研究灵敏度参数随外激励频率、设计变量的变化规律．本文在分析声辐射功率对结构设计参数的灵敏度基础上，结合泰勒展开式，开展结构－声辐射优化研究．最后，运用有限元法－边界元法对双层加肋圆柱壳结构进行结构－声辐射优化分析．

1 结构动力响应

在结构动力响应分析中，设流场中连续结构体受到外力F（x，t）作用，流体对结构的影响写成附连水质量形式，在结构域ΩS内，结构动力响应微分方程为

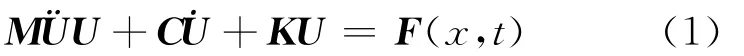
式中：U为节点位移向量；M 为质量矩阵；K为结构刚度矩阵；C为结构黏性阻尼矩阵．质量矩阵M可写成M＝Ms＋Mf，其中：Ms为结构质量矩阵；Mf为附连水质量矩阵．

设外激 励 力 为：F（x，t）＝f（ω）eiωt．式 中：f（ω）为外力幅值；ω为圆频率．节点位移向量写成：U（x，t）＝u（ω）eiωt．式中：u（ω）为节点位移列向量．代入式（1），可得算子方程：［A（ω）］［u（ω）］＝f（ω）．式中：［A（ω）＝－ω2M＋iωC＋K．结构表面节点速度向量v（ω）∶vn（ω）＝iωNA－1（ω）f（ω）．式中：N为与结构的表面形状有关的法向矢量矩阵．法向速度矢量在声边界元法分析中作为边界条件．

2 声辐射功率灵敏度方程

2.1 结构声辐射功率方程

描述结构声辐射能量流在假定的积分面上的属性可用辐射声功率W 来表示．如不考虑声能量在流体中传播时的损失、忽略结构对声能量的吸收，在外声场中声能量与结构表面声辐射能量相等．对于连续振动结构体，在声辐射表面处的声辐射功率为

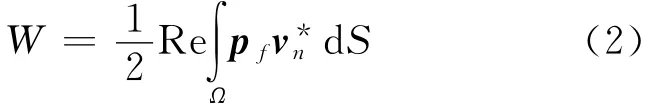
式中：S为是结构－流体交界表面；pf结构表面处声压值为结构表面法向共轭速度；Re为取实部．将结构－流体交界表面离散成M 个单元和N个节点，结构辐射声功率为M个单元的声辐射之和，即：．式中：Sj为第j个单元积分面；vnj为第j单元的法向速度，其值由该单元上的节点法向速度决定．

2.2 声辐射功率灵敏度性分析

灵敏度反映目标函数与设计参数之间的关系，灵敏度的大小决定了设计参数优化方向．根据设计参数的声辐射灵敏度，可定量地获得结构参数的扰动对声辐射水平改变的程度．

声辐射灵敏度为辐射声功率的局部微分，微分变量可以是节点法向速度、结构设计变量、频率等参数．其灵敏度最终取决于结构的阻抗矩阵、激励频率的大小、振动速度、结构形函数等因素．声辐射功率是一个标量，可直接进行微分，将式（2）中对声功率某个设计参数进行微分，即可求出声功率对结构参数的灵敏度

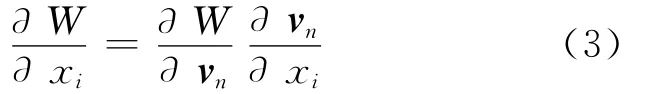
式中：节点对设计参数灵敏度可通过对方程vn（ω）＝iωNA－1（ω）f（ω）微分得到，振动速度的灵敏度取决于振动速度、激励频率以及结构的质量、刚度、阻尼矩阵．

2.3 声辐射功率优化方程

结构－声辐射优化是在设计空间内搜索一组设计变量，使结构的声辐射最小．将声辐射功率替代声压定义为优化目标有一定的特点：将矢量参数的求解变成标量参数的求解；不需要求指定场点处的声压等．结构－声辐射优化问题可写成

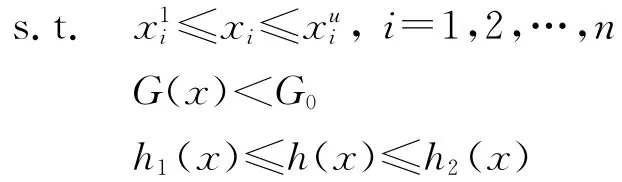
3 结构－声辐射功率函数泰勒展开式

设连续结构体在流场中的声辐射功率f（xi）是某个定义设计变量参数xi的函数，它们之间的关系可用泰勒展开式来表达

式中：f′（xi0）为声辐射功率函数对第i个设计变量在初始设计点xi0处的一阶导数，其实质是声辐射功率函数对该设计变量在设计点xi0处的灵敏度值．由式（5）可知，在求得函数在初值处各阶导数后，结合设计变量的变化量可计算出结声辐射功率函数f（xi）的近似值．

在数值计算中，采用差分法来计算函数的各阶导数．差分法的基本原理是使设计变量在初始设计域附近有一个微小的摄动量Δxi，通过分析其相应的输出响应值，由差分格式计算目标函数f（xi）关于设计变量xi的近似导数．中心差分法具有二阶精度，用中心差分法求得声功率灵敏度后，将其代入式（5），可得到具有二阶精度的声辐射功率的近似公式

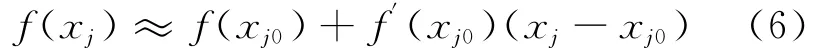
式中：在初值函数值f（xj0）和其导数f′（xj0）为已知条件下，改变参数（xi－xi0）大小即可求得到在初始设计点领域内的结构－声辐射功率值，实现减少结构－声辐射功率之目的．同样，式（7）也适用于场点声压的优化分析．

式（6）中，需假设设计变量的变化量（xixi0）较小，设计变量的变化对结构总体刚度影响较小、对声辐射模态的影响也较小．在设计变量的初始值领域内，声辐射功率与设计变量的变化量近似满足线性关系．当（xi－xi0）值较大时，式（6）中的线性关系将不再满足，对此需通过逐步迭代，在每次迭代后求取该函数灵敏度，并将其代替xj0）进行计算．

4 数值算例

以一个处于水中双层加肋圆柱壳结构受到谐外力作用下的声辐射计算为例，来验证运用灵敏度信息进行结构－声辐射优化的可行性和有效性．

4.1 模型描述

加肋圆柱壳结构见图1．

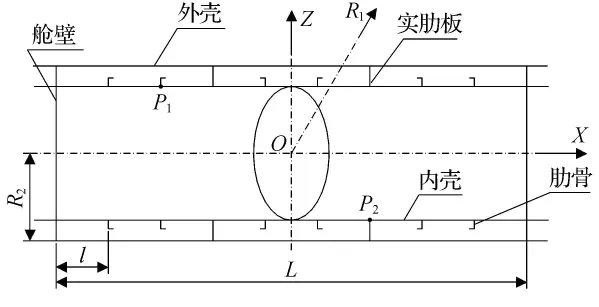
图1 双层加肋圆柱壳

加肋圆柱壳结构参数：外壳半径：1．6m；外壳板厚：0．008m；内壳半径：1．2m；内壳板厚：0．012m；实 肋 板 间 距：1．8m；实 肋 板 厚：0．008m；肋骨间距：0．6m；舱壁厚：0．008m；肋骨：角钢．

结构材料为钢，其力学特性为：密度ρ＝7 800 kg／m3；弹性模量E＝210GPa；泊松比μ＝0．3．设只有外壳的外表面与水接触，水密度ρ＝1 000 kg／m3，水中声速c＝1 490m／s．声功率参考值：W0＝1×10－12W，声压参考值：p0＝1×10－6Pa．

外激励力中心频率为56Hz，作用于内壳上．一个力作用于P1点，大小为 ＜0，0，200．0＞ N．另一个力作用于P2点，大小为 ＜0，0，－200．0＞N．

4.2 结构－声功率灵敏度分析

圆柱壳结构被离散成1 538个节点和1 624个单元．用有限元法进行结构动力响应分析，将节点法向速度作为边界条件，用边界元法计算结构在流场中的声辐射功率，并得到声功率灵敏度．

将圆柱壳结构的外壳与内壳各分成12个部分，并按X方向编号，将结构板厚定义为设计变量．在结构－声功率及其灵敏度数值计算中，频率从0～200Hz，计算步长为1Hz．图2所示为声辐射功率分别对设计变量inner01和outer06的灵敏度．其中，inner01是内壳结构，outer06为外壳结构．在56Hz处，声辐射功率灵敏度对设计变量inner01有最大值，对设计变量outer06有最小值．

由结构－声功率灵敏度值，结合泰勒展开式，通过减少设计变量inner01值可降低所定义的频率处的结构最大声辐射功率；同样，通过增加设计变量outer06也能减少最大声辐射功率．

图2 声辐射功率灵敏度

4.3 声功率灵敏度的应用

结合式（6），应用灵敏度信息进行结构－声辐射优化，是在满足约束条件下减少最大的声辐射值，其中一个约束条件是优化后的结构质量不超过初始设计结构质量．如图2所示，将设计变量inner01的厚度减少0．001 5m，同时对设计变量outer06的厚度增加0．001m（该值的确定是考虑到与inner01值相协调以保证结构总重量不增加）．通过这样的设计更改后，计算出修改后的结构的声辐射功率和指定场点处的声压．

图3为结构修改前后的结构－声辐射功率级，其最大声功率级减低了约4dB．图4为结构修改前后在场点处（0，0，20）的声压级，最大声压级减低了约2dB．

图3 声功率优化

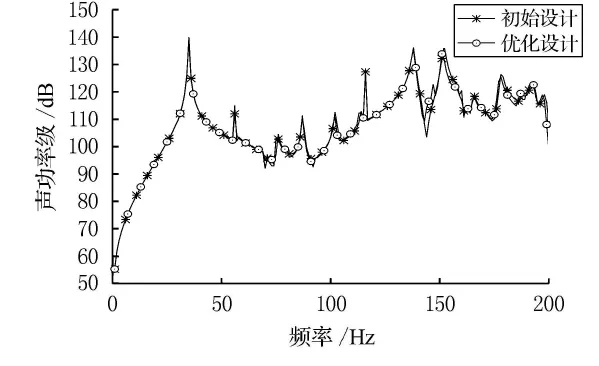
图4 声压优化

由图3～图4可知，通过应用灵敏度信息进行结构尺寸修改，结构的声学特性有了一定的改善，故有效地运用灵敏度信息可在一定程度上实现优化的目的．

4.4 声辐射功率优化

运用声辐射功率灵敏度信息，将设计变量进行修改可一定程度上实现减低结构声辐射功率目的．同样，运用灵敏度信息，对多个设计变量进行参数修改，以实现结构－声辐射的优化．在优化过程中，优化约束满足式（5）要求．

表1所列为结构的部分设计变量在优化前后的变化．图5所示为在优化前后的结构声辐射功率级，其最大辐射功率级减少了约9dB．图6所示为在场点（0，0，20）处优化前后的声压级，其最大声压级减少了约4dB．

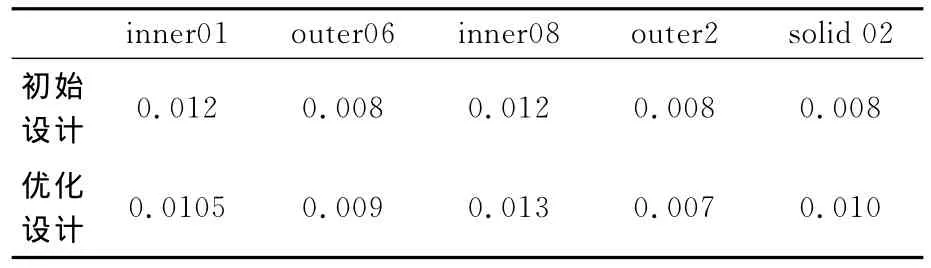
表1 结构设计变量 m

图5 声功率优化

图6 声压优化

由图5～6可知，通过应用多个设计参数的修改进行结构优化，其声学性能有了很大的改善，有效地运用灵敏度信息可在一定程度上实现优化的目的．对于复杂结构，要实现多个变量、多目标函数优化，需综合运用灵敏度信息与合适的优化平台及和搜索策略才能实现．

5 结束语

文章分析了圆柱壳结构的声辐射功率灵敏度，并将其应用于声辐射优化，其声辐射功率最大峰值有了明显减低，同样在声场点的声压明显减少．结果表明，用功率灵敏度结合泰勒公式进行声辐射优化具有一定可行性，是结构－声辐射优化设计的一个重要发展方向．

［1］KIM N H，DONG J，CHOI K K，et al．Design sensitivity analysis for sequential structural－acoustic problems［J］．Journal of Sound and Vibration，2003，263（3）：569－591．

［2］WANG S Y，LEE J．Acoustic design sensitivity analysis and optimization for reduced exterior noise［J］．AIAA Journal，2001，39（4）：574－581．

［3］CHENG H，CHEN J，ZHANG Y B，et al．A multidomain boundary element formulation for acoustic frequency sensitivity analysis［J］．Engineering Analysis with Boundary Elements，2009，33（6）：815－821．

［4］MARBURG S．A general concept for design modification of shell meshes in structural－acoustic optimization－Part I：Formulation of the concept［J］．Finite Elements in Analysis and Design，2002，38（8）：725－735．

［5］MARBURG S，HARDTKE H J．A general concept for design modification of shell meshes in structuralacoustic optimization－Part II：Application to a floor panel in sedan interior noise problems［J］．Finite Elements in Analysis and Design，2002，38（8）：737－754．

［6］LI D S，CHENG L，GOSSELIN C M．Optimal design of PZT actuators in active structural acoustic control of a cylindrical shell with a floor partition［J］．Journal of Sound and Vibration，2004，269 （3－5）：569－588．

［7］陈美霞，杜 磊，陈乐佳，等．基于边界元法的平板结构声振性能数值计算［J］．武汉理工大学学报：交通科学与工程版，2009，33（6）：1048－1051．

［8］丁少春，朱石坚，俞 翔，等．运用功率流方法对舰艇水下声辐射特性的研究［J］．武汉理工大学学报：交通科学与工程版，2008，32（2）：263－266．

［9］孙淦云，王跃方．密闭腔体声－结构耦合系统的动力灵敏度分析［J］．计算力学学报，2005，22（5）：550－554．

［10］张 军，兆文忠，张维英．结构声辐射有限元／边界元法声学－结构灵敏度研究［J］．振动工程学报．2005，18（3）：366－370．