求解价格控制问题的旋转算法＊

金照林 胡铁松

（武汉长江工商学院1） 武汉 430065）

（武汉大学水资源与水电工程科学国家重点实验室2） 武汉 430072）

0 引 言

对于价格控制问题，滕春贤等［1］研究了价格控制问题解集的基本性质以及连通性．阮国桢等［2］在理论分析的基础上提出了求解价格控制问题的单纯形算法．周水生等［3］利用下层问题对偶间隙为零的原理提出了价格控制问题的罚函数方法．

文中在旋转算法的基础上，对其进行了改进，发挥了该算法原理简洁、实际计算效率高且容易学习理解的优点，用于求解价格控制问题．如稍加变通，该方法还可用来求解其他主从递阶决策问题，例如线性二层或多层规划问题等，显示了该算法在求解此类问题上的优势．

本文采用“由上至下”的方式，根据算法的特点，可以便利地构造割平面约束，使用算例证实了该方法的有效性．

1 相关理论

价格控制问题假定上层决策者控制价格变量x，以优化其收益函数aTx＋bTy．式中：y为n种产品的产量，下层决策者在上层决策者宣布价格策略以后，通过调整其产量y，以优化其收益目标xTy．由上所述，价格控制问题的一般数学模型为

式中：x＝（x1，x2，…，xn）T为上层控制的决策变量；y＝（y，y，…，y）T为下层控制的决策变量；

12n上、下层的目标函数分别为f1（x，y），f2（x，y），a∈Rn，b∈Rn；A为m×n阶矩阵；B为m×n阶矩阵．

定义1 对于问题（1），集合S＝｛（x，y）｜Ax＋By≤r｝称为它的容许集．S显然是闭凸集，这里假设S是有界的．

定义2 S中的点（x，y）称为问题（1）的可行点，若对于这个x，y恰好是下层问题的解．一切可行点的集合记作S1，S1称为问题（1）的一层可行集，S称为二层可行集．

由于容许集S为多面凸集，但可行集S1一般不是凸集，因此价格控制问题（1）一般是非凸规划问题．下层问题的目标函数xTy为线性函数，但由于系数向量x是不断变化的，这表明价格控制（式（1））也可以被归为非线性二层规划问题．

文献［1］阐述了有关价格控制解的最优性条件，本文直接引用了原作者的论述．

定理1 S中的点（x，y）为可行点（即（x，y）∈S1）的充要条件是：存在ω≥0，ω∈Rm，使得ωTB＝xT，ωT（Ax＋By－r）＝0．

推论1 S中的点（x，y）为可行点的充要条件是：存在ω≥0，（ω∈Rm），使得ωTB≥xT，ωT（Ax＋By－r）＝0．

推论2 （x＊，y＊）是式（1）的最优解的充要条件是，存在ω≥0，（ω∈Rm），使得（x＊，y＊，ω＊）为下述式（2）的最优解

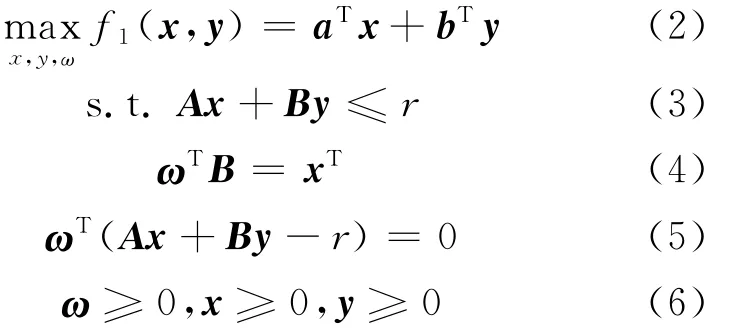
推论2说明式（1）与式（2）是等价的，其中约束条件（3）与ω≥0称为互补不等式，约束条件（5）为互补松弛条件．

2 使用旋转算法求解价格控制问题

对价格控制问题以及线性二层规划问题的求解，吕一兵提出了基于罚函数的修正Frank－Wolf方法［5］，但该算法通常仅能得到问题的局部最优解．本文在张忠桢先生提出的旋转算法的基础上［6］，对其进行了改进，并应用于解决线性主从递阶问题，显示了其相比于以往传统方法的优势．

2.1 算法的思想

使用旋转算法求解价格控制问题大体有两种思路，一是“由上至下”的方法，即先不考虑互补松弛条件而直接求得式（2）（典型的线性规划问题）的最优值，然后再“由上至下”逐顶点检查是否满足互补松弛条件，该方法毫无疑问可以找到问题的全局最优解，但在求解大型问题时可能会导致计算量和存储量较大．第二种思路是“由下至上”的方法，即从某一个初始点出发，在满足所有约束条件的基础上目标函数向更优的方向迭代，例如罚函数法，该思路计算量较小，但容易最后获得的解为局部最优．

使用旋转算法求解价格控制问题时，以上两种思路都是可行的．对于“由下至上”的方法，由于要维持互补条件，因此在旋转运算枢轴元素只能在运算表的主对角线上的元素中选择，而当主对角线上的元素为0时，则使用双枢轴旋转运算同样可以维持互补松弛条件．限于篇幅的原因，本文仅介绍第一种方法即“由上至下”的方法．

使用“由上至下”的方法，计算过程分为两个阶段：

第一阶段：先不考虑互补松弛条件（5），此时原问题是一个典型的线性规划，使用旋转算法可以很容易找到其最优解．第二阶段：逐极点测试是否符合互补条件，一旦找到即为问题的全局最优解．

如何实现从上至下逐极点测试，文献［7］提出的极点排序法和文献［8］中的分支定界法存在的问题是计算量和存储量较大，而赵贸先［9］提出使用相邻的极点来构造割平面的想法可以有效解决这一问题．

设多面体S＝｛x∈Rn｜Ax≤b｝（其中A＝（aij）∈Rm×n，b＝（b1，b2，…，bm）T∈Rm，m≥n），如S 是非退化的，x0是S的一个极点，则x0在S中有n个相邻的极点，记为（x1，x2，…，xn）．

令Q＝（x1－x0，x2－x0，…，xn－x0）为一个n阶方阵，e＝（1，1，…，1）为一个n阶行向量．由线性规划基本理论知向量组Q线性无关，因此Q－1存在，并且由等式eQ－1（x－x0）＝1决定的超平面将通过每一个x0相邻的极点x1，x2，…，xn，称上述超平面为极点x0对应的割平面，相应的割为eQ－1（x－x0）≥1．

记S＊＝｛x∈S：eQ－1（x－x0）≥1｝，¯S＝｛x∈S：eQ－1（x－x0）＜1｝．下述定理2说明由极点x0对应的割平面在切割多面体的一部分¯S后，余下的S＊是S的一个非空子集．且为非退化的多面体．

定理2 设多面体S是非退化的，则S＊是非退化的，则S＊∪¯S＝S，S＊∩¯S＝∅．

根据以上结论，首先用旋转算法在第一阶段不考虑互补松弛条件，求出式（1）的最优解（x0，y0）为S上的一极点后，然后判断是否满足互补条件，如果满足则问题已获得全局最优解；否则根据定理5，引进极点（x0，y0）对应的一个割平面，使得S中被割去的部分S不含该价格控制问题的任何一个可行解，且保证余下的部分S＊也是一个非退化的多面体．重复上述过程．因为每进行一次割操作都将割去原约束域上的一个极点，而这种割操作不会增加约束域上的极点，并且S的极点有有限个，所以经过有限步后一定能找到S上的一个极点为该价格控制问题的全局解．

以上方法在构造割平面时需要使用矩阵求逆运算，而使用旋转算法在表上运算时更为简便，方法见表1．

表1 约束e为相邻极点构造的割平面

在表1中，如果ωrs＊和ωij＊为可行的枢轴元素，实际为以当前已入基的约束as和aj决定的极点的2个相邻极点所对应的基，最下行约束d为当前极点的相邻极点组成的割平面．

利用上述思想，现将求解价格控制问题的算法步骤描述如下．

步骤0 令S0＝S，置k＝0，转步骤1．

步骤2 对给定的xk，判断是否满足互补松弛条件，如满足，则停止，（xk，yk）为价格控制问题的全局解；否则，转步骤3．

步骤3 用旋转算法找到点（xk，yk）在Sk中的所有相邻极点，并按照表2的方法构造相对应的割平面约束d，转步骤4．

步骤4 令Sk＋1＝｛（x，y）∈Sk∩d｝，转步骤1．

2.2 算法示例

相关文献在验证其理论与算法的时候大都使用如下实例．在运算开始前，先将各约束条件编号为a1～a3，对于基本的可分离变量的约束条件编号为e11～e22．

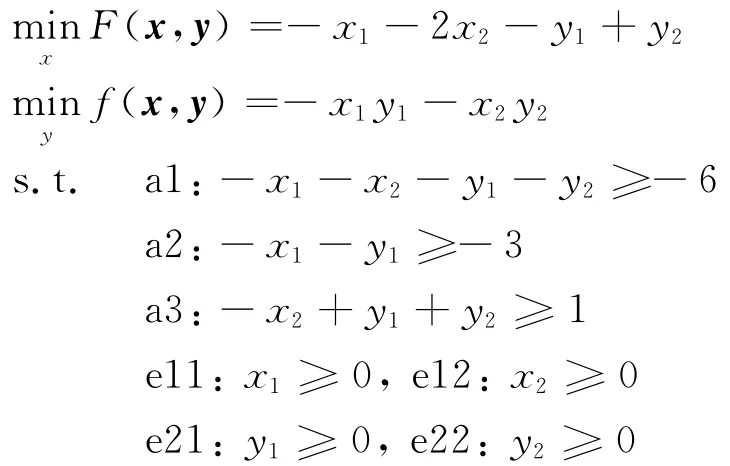
为便于理解，在以下旋转运算表中，单元格为灰色底纹表示该元素作为枢轴迭代后得到的解（x，y）∈S，单元格有边框表示最终选定该元素为枢轴进行下次迭代．

求解过程为：

步骤0 形成上下层初始运算表．由式（2）在忽略互补松弛条件后，可得如下初始表2，其中标记h1，h2，u1，u2 ，u3分别为e21，e22，a1，a2，a3对应的互补不等式．

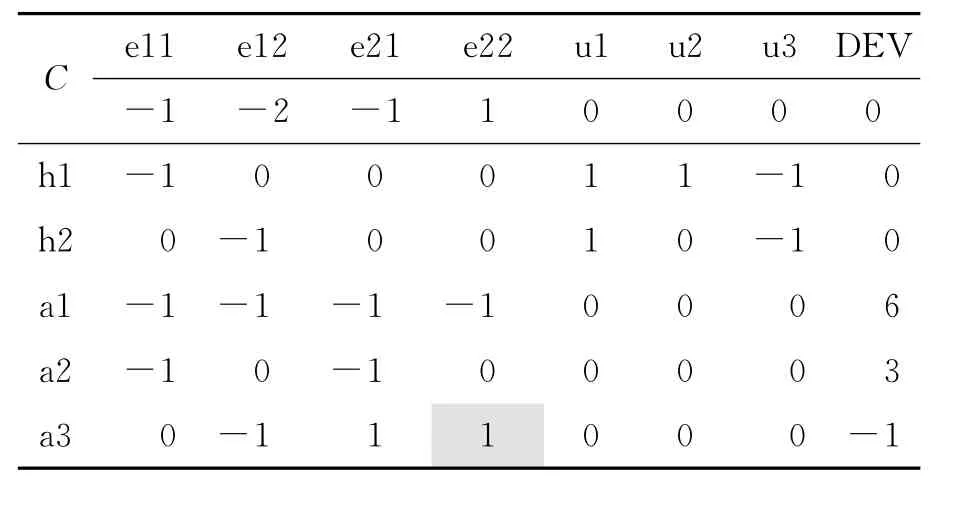
表2 初始旋转运算表

在运算表中，C表示上层问题的约束条件系数．当初始值对应的目标函数值为0时，在偏差列DEV中，C行中的元素实际为上层问题的目标函数值．

从上表可以看出，由于约束条件a3偏差小于0，因此该不等式为违反不等式，需要进行迭代使其进入容许集S，由表1可知，欲使同行偏差非负，可以选取（e22，a3）为下次迭代的枢轴元素．

步骤1 进入约束域后，暂不考虑互补条件，使用旋转算法求解线性规划问题．

由于上步旋转运算后中所有偏差非负，说明迭代已进入容许集，为求得线性规划问题最优值，需要将C行所有的约束条件系数变为非负数，因此可以依次以（a2，a3）、（h2，x2）、（a3，u1）和（a1，e22）为枢轴元素，得到表3．

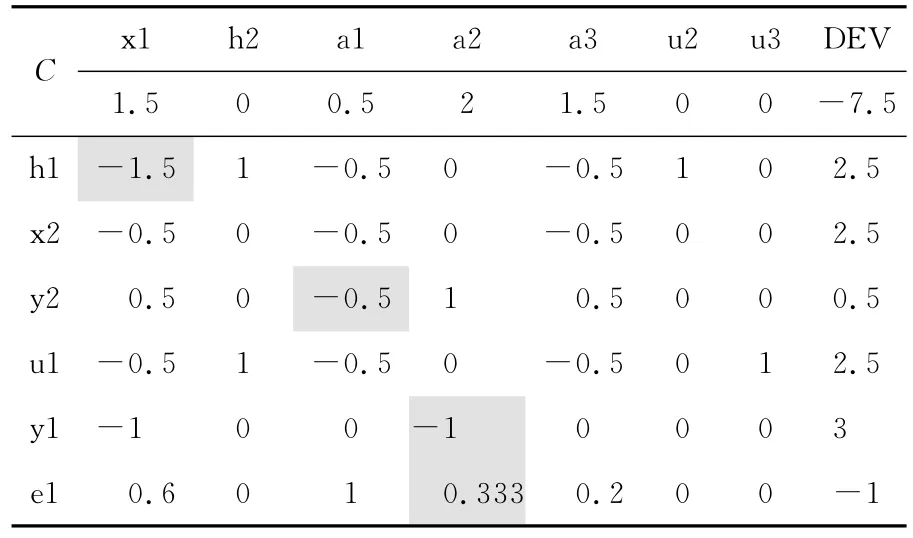
表3 旋转运算表（求线性规划问题最优值）

步骤2 增加割平面约束，逐步极点搜索．

由表3可见，由于约束条件h1和e21必须有一个入基，因此该极点不符合互补条件．可构造切割面e1，并使用旋转算法求解新的线性规划问题的最优解，得表4．

由表4可见，由于h1，e21和u1，a1均在基外，因此需要根据相邻极点构造新的割平面约束e2，列在表4的最末行中，并使用旋转算法求解新的线性规划问题的最优解，得表5．

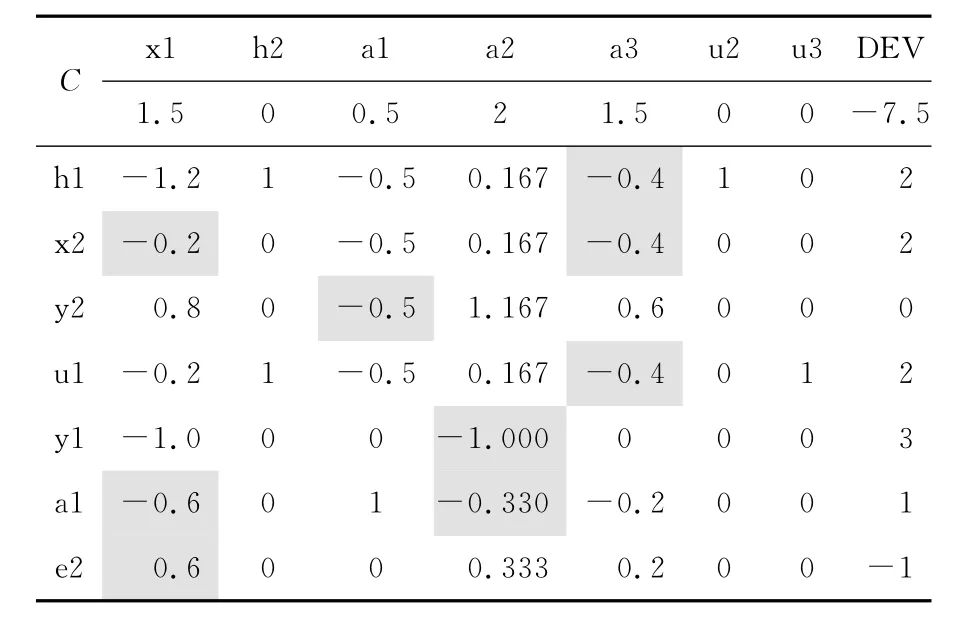
表4 旋转运算表（求线性规划问题最优值）

表5 旋转运算表（求线性规划问题最优值）

表5整理后，测试后发现已满足所有互补条件，可删除所有割平面约束，计算终止．

因此，该价格控制问题的全局最优解为x1＝5／3，x2＝5／3，y1＝4／3，y2＝4／3，上下层目标函数值分别为F＊＝5，f＊＝40／9．以下是相关文献的计算结果．

表6 算例结果对比

由表6可见，计算结果优于文献［2－3］，与文献［10］相同，但计算过程更为简便．注意到该解并不是容许集的极点，同时在x1＝5／3，x2＝5／3时，下层的反馈并不惟一，实际上该解为乐观解．

3 结束语

使用旋转算法来求解价格控制问题，并使用了更为简便的增加割平面约束的方法计算全局最优解．如将该算法稍加变通，还可以求解包括线性多层规划以及一主多从（或有共享变量的）的二层规划（将另文说明），显示了该方法在解决主从递阶问题上的优势．

对于一多面体，当出现退化的基本可行解时，它必然位于多于n个（线性无关）超平面的交集上，此时相应极点的相邻极点的会出现多于n个的情况，而如何搜索出这所有的极点，本文采用的是遍历的方式，即遍历所有的基组合，而寻找出当前极点对应的相邻极点，这样会使运算量大增，这需要对退化情况下凸规划理论进行更深入地研究．

［1］滕春贤，李智慧，李 磊．价格控制问题解集的基本性质和连通性［J］．系统工程理论与实践，1997（2）：45－49．

［2］阮国桢，杨丰梅，汪寿阳．线性二级价格控制问题的单纯形方法［J］．系统工程理论与实践，1997，16（12）：38－43．

［3］周水生，刘三阳，刘红英．价格控制问题及其推广形式的罚函数法［J］．系统工程学报，1999，14（2）：156－159．

［4］LORIDAN P，MORGAN J．Weak via strong stackelberg problem：new results［J］．Journal of Global Optimization，1996（8）：263－287．

［5］吕一兵．一种求解线性二层规划的修正Frank－Wolf方法［J］．武汉理工大学学报：交通科学与工程版，2005，29（6）：993－996．

［6］张忠桢．凸规划－投资组合与网络优化的旋转算法［M］．武汉：武汉大学出版社，2004．

［7］BIALAS W F．KARWAN M H．Two－level linear programming［J］．Management Science，1984（30）：1004－1020．

［8］BARD J F．MOORE J T．A branch and bound algorithm for the bilevel programming problem［J］．SIAM Journal of Scientific and Statistical Computing，1990，18：35－42．

［9］赵贸先，高自友．求解线性双层规划的割平面算法［J］．北京交通大学学报，2005，29（3）：65－67．

［10］刘志勇，滕春贤，陈东彦．关于二层价格控制决策问题的探讨［J］．统计与决策，2007，248（20）：37－42．