烷基自由基β位裂解反应类反应势垒与速率常数的精确计算

汪必耀 谈宁馨 姚 倩李泽荣,* 李象远

(1四川大学化学学院,成都610064; 2四川大学化学工程学院,成都610065)

1 引言

燃料在发动机燃烧室的点火成功与否以及燃烧释放的能量是否达到发动机的需要,会大大影响发动机的工作效率.因此对燃烧的详细反应机理的研究是一项非常有意义的工作.碳氢燃料是自然界最普遍的燃料,然而碳氢燃料的燃烧是一个复杂的过程,燃烧的详细反应动力学机理含有大量的基元反应,涉及到数百种物质和成千上万个反应,1,2复杂的反应机理使得即使较为简单的燃烧现象也难于模拟.但在这成千上万个反应中,很多反应属于相同的一类,3,4而反应类的数目是有限的,这成为很多机理自动生成的出发点.碳氢燃料的燃烧模拟在燃烧机理的研究中起着越来越重要的作用,而可靠的详细反应机理(包括反应列表、热力学数据和动力学数据)是其关键.碳氢化合物的燃烧和裂解中都涉及到大量的裂解反应,目前仅有少数简单碳氢化合物自由基裂解反应的动力学实验数据有文献报道.5-9烷基自由基β位裂解反应是一类生成小分子烯烃和烷基的重要燃烧反应,在温度较高的燃烧体系中此类反应有着举足轻重的作用.10

近年来,Truong等11-17把反应类过渡态理论概念引入到动力学计算中,此方法基于传统过渡态理论并能结合较低水平从头算方法精确计算同一类反应的速率常数.反应类过渡态理论的基本思想是同一类反应中所有反应均有相同的反应中心,即沿着反应坐标的势能面上存在某些相似之处.对于和主反应同类的其他反应的速率常数仅从它们间的势垒差与主反应的速率常数就可准确计算得到.根据Truong等11-17的研究结果发现,同类反应中的某些热力学性质是近似不变量,如过渡态的振动虚频、参考反应与目标反应的势垒差等.由于参考反应与目标反应的势垒差随不同从头算理论方法的变化不大,反应类过渡态理论即可通过低水平的从头算理论方法精确计算大分子体系的动力学性质.对于参考反应与目标反应间的势垒差不随不同精度从头算方法变化而变化的原因,Truong等并没有做进一步阐述.众所周知构建等键反应方法计算的反应焓变随不同水平从头算方法的变化不大,18,19因为在等键反应中反应物和产物所有键的类型和数目都是守恒的,由非完全基组和电子能量修正所导致的误差在计算反应焓变时得以抵消,20继而提高计算精度.而本文将把等键反应引入到同类反应动力学性质的精确计算中,并称其为反应类等键反应方法.

2 理论方法

在同一类反应中取任意两反应,其中RP为主反应,RT为目标反应:

反应(1)和(2)对应的过渡态生成反应分别为:

其中ΔVP≠和ΔVT≠分别为反应(3)和反应(4)的反应能,即分别为主反应RP和目标反应RT的反应势垒.由式(4)减去式(3)得到以下反应:

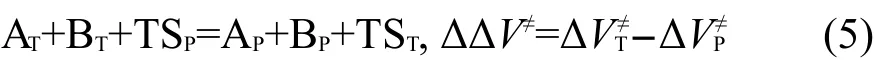
其中ΔΔV≠为该反应的反应能,即目标反应RT和主反应RP的势垒差.由于反应(5)涉及过渡态,而过渡态的几何结构常涉及扭曲的化学键,所以不能按传统的等键反应方法通过计算反应前后典型键的数目来判断反应是否为等键反应.由于反应(5)为同一类型的两反应对应的过渡态的生成反应相减得到,而同一类型的两反应有相同的反应中心和不同的取代基团,则反应(5)可以划分为两部分:两反应涉及的取代基团和两反应的反应中心,可以很容易证明取代基团涉及到的典型键的数目在反应(5)的反应前后是相同的.如果两反应的反应中心的几何结构相同或非常接近,我们可以把反应(5)视为等键反应.在这种情况下,根据等键反应原理,ΔΔV≠为等键反应的反应能,应随从头算理论水平的变化而变化不大,即通过低水平从头算方法亦能得到较精确的计算结果.设反应势垒ΔVP≠ʹ、ΔVT≠ʹ为可靠实验值或高水平从头算方法的计算结果,而反应势垒ΔVP≠、ΔVT≠由较低水平从头算方法计算得到,则它们应近似地满足以下关系式:

因而有:

其中:ΔΔVP≠为主反应精确反应势垒和近似反应势垒的差值,即主反应的反应势垒的修正值.式(7)即为利用反应类等键反应方法计算目标反应的精确反应势垒的表达式,表明目标反应的精确反应势垒可以由其低水平计算的近似结果通过主反应的修正值修正得到.这就解释了Truong等在反应类过渡态理论里所涉及到同类反应中主反应与目标反应的势垒差值不随从头算水平变化而变化的表述.由于精确计算只涉及到主反应而不涉及目标反应,所以目标反应只涉及到低从头算水平的近似计算,而主反应又通常选择较小的分子反应体系.因此根据该修正方法,可以在低从头算水平下得到目标反应的精确反应势垒,从而解决了大分子反应体系动力学参数的精确计算问题.

烷基自由基β位裂解反应是碳氢化合物在高温条件下燃烧所涉及的非常重要的一类反应,10其裂解产物为烯烃和烷基自由基.本文选取了以下13个烷基自由基的β位裂解反应作为研究体系,以检验反应类等键反应方法的计算精度及普适性:

其中最小的反应体系R1选为主反应.所有反应涉及到的物种的几何结构优化和频率计算均在BHandHLYP/cc-pVDZ水平下进行,并用内禀反应坐标(IRC)理论21对体系中反应通道进行了确认.由于主反应R1的反应势垒没有相关的实验数据和文献报道,因此本文选用高精度CCSD(T)/cc-pVXZ (X=D,T,Q)22-26方法外推到完全基组法计算主反应中各物种的精确单点能:

其中,Hartree-Fock完全基组能量EHF∞由HF/cc-pVXZ (X=D,T,Q)外推得到:

完全基组相关能Ecor∞由CCSD(T)/cc-pVXZ(X=D,T)外推得到:

通过式(11)求得的各物种的单点能进一步用于计算主反应的精确反应势垒∆V1≠ʹ.本文选取了5个目标反应R2、R3、R4、R5、R6作为测试集,用不同从头算近似方法直接计算了这5个目标反应的反应势垒,进一步用反应类等键反应方法进行了修正,并与高精度从头算方法的结果进行比较.本文共考察了10种近似从头算方法,标记为L1,L2,…,L10,他们分别是:L1:HF/cc-pVDZ;L2:BHandHLYP/cc-pVDZ;L3: B3LYP/cc-pVDZ;L4:BP86/cc-pVDZ;L5:TPSS/ccpVDZ;L6:B3P86/cc-pVDZ;L7:O3LYP/cc-pVDZ; L8:MP2/aug-cc-pVDZ;L9:CCSD(T)/cc-pVDZ;L10: CCSD(T)/aug-cc-pVDZ.这些方法可划分为四个级别:Hartree-Fock(L1),DFT(L2-L7),MP2(L8),CCSD所有从头算计算均在Gaussion 03程序27上完成.

3 结果与讨论

3.1 过渡态的反应中心几何结构

用BHandHLYP/cc-pVDZ方法优化后的过渡态反应中心所涉及到的原子、键长与键角编号如图1所示.其中d1、d2为键长,A1为键角,Ra、Rb、Rc、Rd、Re、 Rf、Rg代表过渡态中烷基或氢取代基.过渡态反应中心的优化几何结构参数列于表1中.

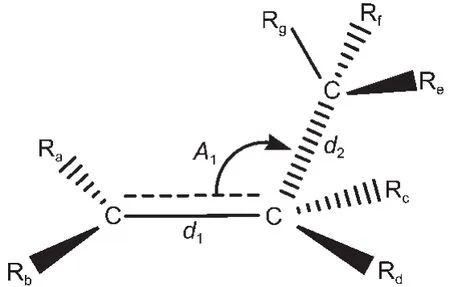
图1 过渡态反应中心的几何结构Fig.1 Geometry structures for the reaction center of the transition state

表1 过渡态反应中心优化后的几何参数Table 1 Optimized geometrical parameters of reaction center of transition state

由表1所列出的数据可以看出,同类反应的过渡态反应活性中心的几何结构几乎相同,新形成的双键d1和将断裂的键d2的最大绝对误差仅为0.0012和0.0044 nm,两者间夹角的最大误差也仅为11.6°,所以由任意两过渡态生成反应所组成的代数差反应中的过渡态反应中心的几何结构是守恒的,由体系中任意两过渡态的生成反应的差所构建的反应即为等键反应.

3.2 不同从头算水平计算的主反应的反应势垒

用选取的10种近似从头算方法及CCSD(T)/ cc-pVXZ(X=D,T,Q)水平下的完全基组外推法计算了主反应的反应势垒,结果列于表2.

表2中的结果显示出不同从头算方法的计算结果相差较大,以精确的完全基组外推法CCSD(T)/ CBS作为不同计算方法对势垒结果影响的比较基准,近似从头算方法势垒值的最大偏差与最小偏差分别来自TPSS/cc-pVDZ方法的12.57 kJ·mol-1和O3LYP/cc-pVDZ方法的-2.11 kJ·mol-1.由此可以看出在本研究体系中,O3LYP/cc-pVDZ方法的计算精度甚至高于CCSD(T)/aug-cc-pVDZ方法.但由于不同DFT方法对不同体系的计算结果相差较大,因此并不具有普适性.而表中∆∆VP≠项用于后文对低水平从头算方法下的目标反应的反应势垒进行校正.

3.3 反应势垒的直接计算与等键反应修正的结果比较

表2 主反应R1在各水平从头算方法下的反应势垒Table 2 Reaction barriers at various ab initio levels for the principal reaction R1

本文从烷基自由基β位裂解反应的体系中选取5个代表反应R2、R3、R4、R5、R6,分别在Hartree-Fock (L1),DFT(L2-L7),MP2(L8),CCSD(T)(L9-L10)水平下对这些反应的反应势垒进行了计算,并用反应类等键反应方法进行了修正,结果列于表3.

由于本文所选择的研究体系缺乏对应的实验势垒数据,因此文中选择以较精确的CCSD(T)/ aug-cc-pVDZ方法(表3中L10)作为不同从头算方法比较反应势垒计算精度的基准.从表3中的数据可以看出,不同从头算方法对同一反应的直接计算结果相差较大,其中最大绝对偏差(MAE)可达17.43 kJ·mol-1,5个代表反应的最大绝对偏差的平均值亦有16.16 kJ·mol-1.而利用反应类等键反应方法校正后的最大绝对偏差为7.64 kJ·mol-1,5个代表反应的最大绝对偏差的平均值也仅有5.32 kJ·mol-1.表明在本体系中用反应类等键反应方法计算的反应势垒对从头算方法的级别和基组的大小依赖性小,反应类等键反应方法在较低从头算水平即可再现较高从头算水平结果.

3.4 目标反应的反应势垒

对于烷基自由基β位裂解反应类中所有目标反应的反应势垒,我们均采用低水平的BHandHLYP/ cc-pVDZ方法并通过反应类等键反应方法校正获得,相应结果列于表4.

3.5 反应速率常数的计算

根据传统过渡态理论,反应:

速率常数k可通过下式计算得到:

其中:κ为隧穿效应引起的穿透系数,kB和h分别是Boltzmann常数和Planck常数,T为热力学温度,R为摩尔气体常数,Q≠、QA、QB分别是过渡态、反应物A、反应物B的配分函数,∆V≠为过渡态电子能量与反应物电子能量之差,即反应的能垒.以上配分函数不包含电子运动的贡献,只包含振动、转动和平动的贡献,仅与优化得到的几何结构和振动频率有关,而与单点能计算无关,因此单点能计算的从头算级别只影响反应的能垒.根据前面引入的反应类过渡态理论,设在某一从头算水平直接计算得到的反应能垒和由反应类过渡态理论修正后的反应能垒分别为∆V≠及∆V≠',计算得到的反应速率常数分别为k及k',则有:

即:

其中:∆∆V≠即为式(7)、(8)定义的能垒修正值.根据式(15),由低水平从头算方法得到的速率常数通过反应类等键反应方法校正可以获得类反应的精确速率常数.

本文中类反应体系的每一个反应的速率常数均通过基于传统过渡态理论框架下的TheRate软件28计算获得,并应用Eckart方法29对隧穿效应进行校正.

与3.4节一样,主反应分别在CCSD(T)/CBS和BHandHLYP/cc-pVDZ水平计算得到能垒修正值为-11.67 kJ·mol-1(见表2).体系中所有目标反应单点能均为BHandHLYP/cc-pVDZ水平.燃烧动力学模拟需要的动力学参数通常是根据改进Arrhenius方程:

其中:A为指前因子,E为阿仑尼乌斯活化能,n为常数.对过渡态理论计算得到的不同温度下速率常数k(T)拟合,以参数(A,n,E)形式给出.

本文为了验证反应类等键反应方法对类反应速率常数的计算精度,对文献7,30-39中有实验速率常数报道的反应R2、R3、R4,用反应类等键反应方法计算了在温度范围为500-2000 K的速率常数,并与文献报道实验值7,30-39进行了比较,比较结果列于表5.为了方便比较,我们定义速率常数比值kmax/kmin为计算值与实验值中较大速率常数与较小速率常数的比值,并将3个代表反应的kmax/kmin在温度范围为500-2000 K下的最大值MD与平均值AD分别列于表5.

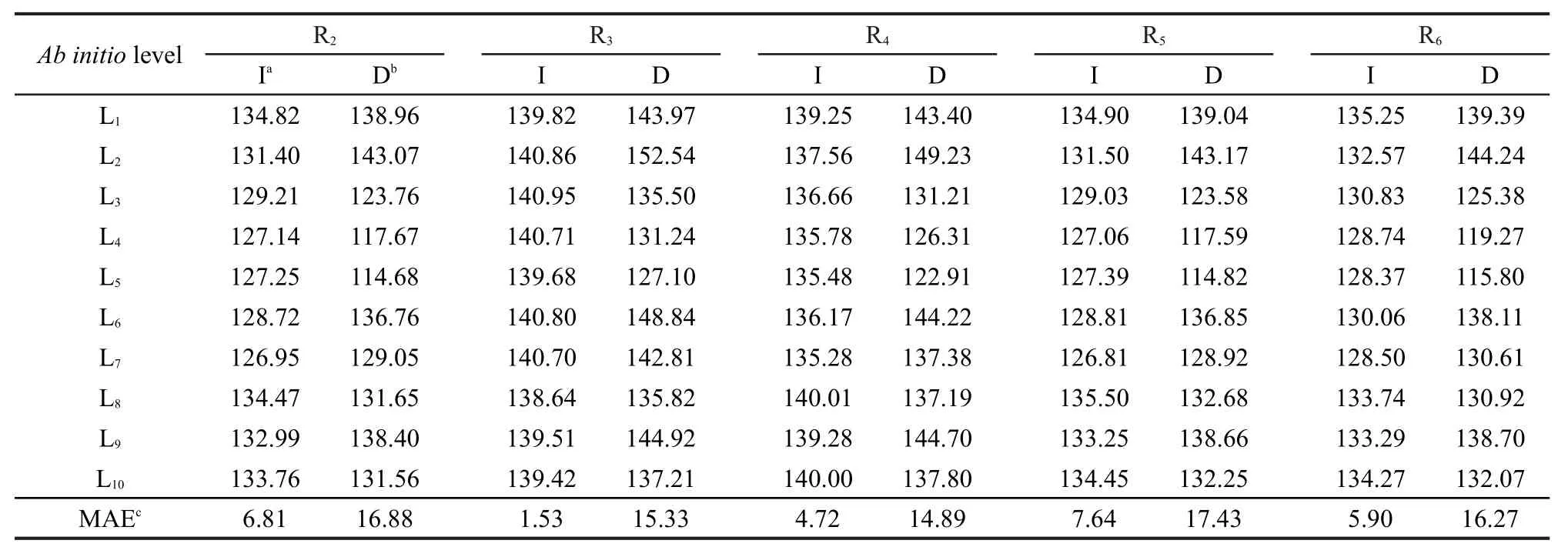
表3 代表反应的反应势垒(单位:kJ·mol-1)Table 3 Reaction barriers of the representative reactions(unit in kJ·mol-1)

表4 由反应类等键反应方法计算的反应势垒Table 4 Reaction barriers calculated by reaction class isodesmic reaction method

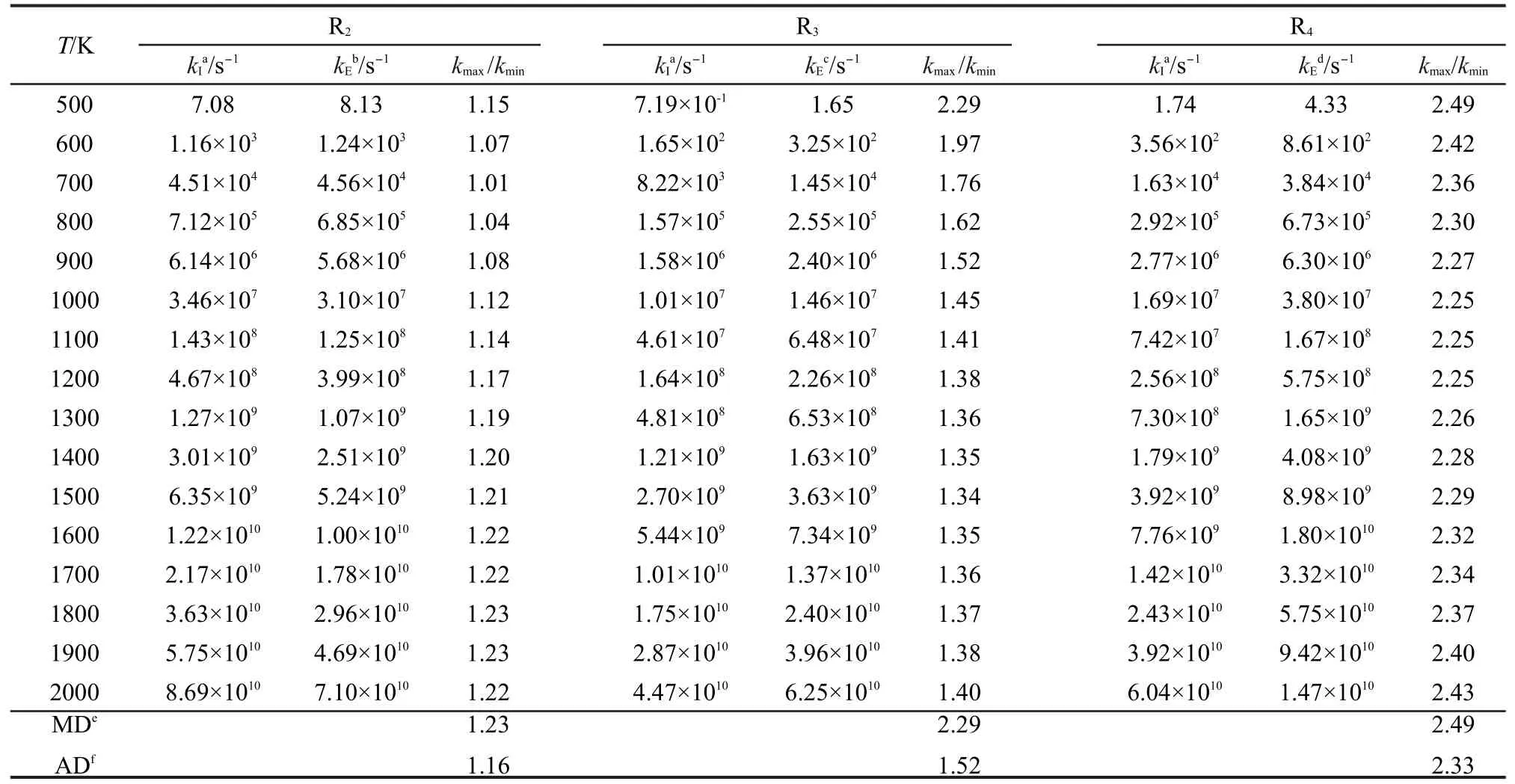
表5 过渡态理论速率常数的反应类过渡态理论方法计算值与实验值的比较Table 5 Comparison of transition state theory rate constants from the reaction class isodesmic reaction method calculations and the experiment values

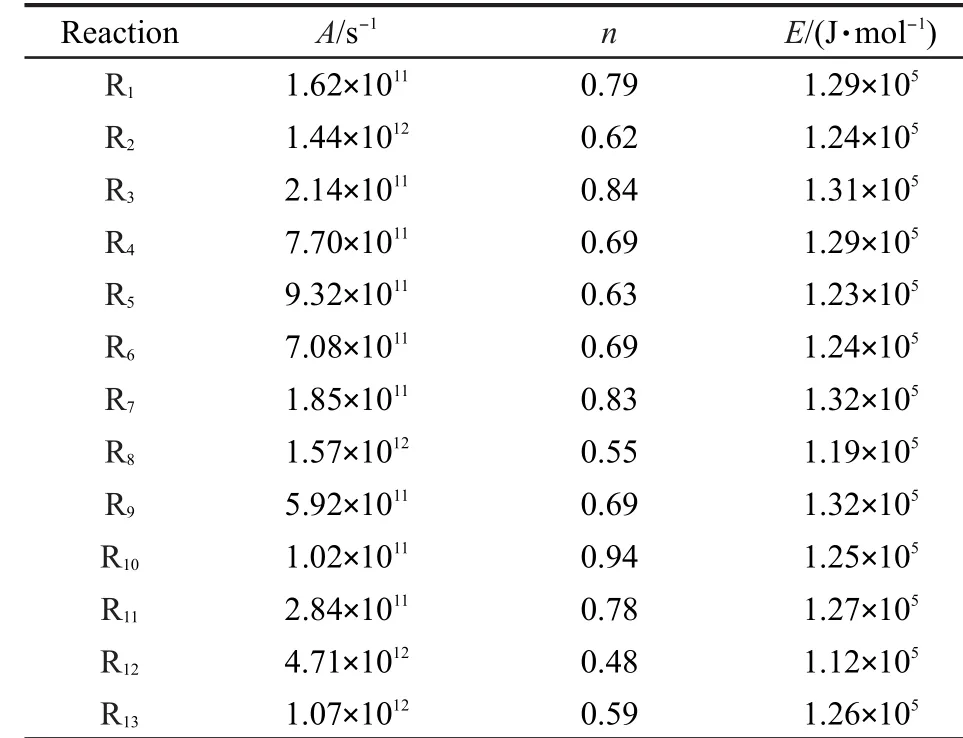
表6 动力学参数(A,n,E)的计算Table 6 Calculated kinetic parameters(A,n,E)

从表5中的数据看出,通过反应类等键反应方法校正后的3个代表反应在温度范围为500-2000 K的速率常数与文献报道的实验值非常接近.3个代表反应在500-2000 K温度内kmax/kmin的平均值仅为1.67,单个反应kmax/kmin的最大平均值也仅为2.33,最大值也只有2.49.因此应用反应类等键反应方法精确校正同类反应低精度下的速率常数是高效而可行的,同时此方法亦能在低计算要求和低耗时情况下获得较高的计算精度,从而为大分子反应的高精度速率常数计算创造了有利条件.

表6给出了由反应类等键反应方法校正得到的速率常数拟合得到的各反应动力学参数(A,n,E).

4 结论

提出了在低从头算水平下精确计算类反应能垒及速率常数的反应类等键反应方法,并用于烷基自由基β位裂解反应体系.通过在不同从头算水平和不同基组下对其中5个代表反应体系的反应能垒的对比计算发现,用反应类等键反应方法计算的反应势垒对从头算方法的级别和基组的大小依赖性小,利用反应类等键反应方法,可将直接从头算方法获得的反应势垒平均最大绝对偏差16.16 kJ· mol-1降低到5.32 kJ·mol-1.用反应类等键反应方法计算了烷基自由基β位裂解反应体系的反应能垒、不同温度下的速率常数,并拟合得到(A,n,E)形式的各反应动力学参数.对其中有文献实验速率常数报道的3个反应,其计算速率常数和实验速率常数比值kmax/kmin在500-2000 K温度段内的平均值仅为1.67,单个反应的最大比值为2.49,表明反应类等键反应方法可计算得到与实验相近的速率常数.因此本文工作表明,反应类等键反应方法可在低从头算水平计算得到类反应体系精确的反应势垒和速率常数,可解决大分子体系动力学参数的精确计算问题.

(1) Lu,T.F.;Law,C.K.Combust.Flame 2006,144,24.doi: 10.1016/j.combustflame.2005.02.015

(2) Pepiot-Desjardins,P.;Pitsch,H.Combust.Flame 2008,154,67. doi:10.1016/j.combustflame.2007.10.020

(3) Curran,H.J.;Gaffuri,P.;Pitz,W.J.Combust.Flame 1998,114, 149.doi:10.1016/S0010-2180(97)00282-4

(4) Curran,H.J.;Gaffuri,P.;Pitz,W.J.Combust.Flame 2002,129, 253.doi:10.1016/S0010-2180(01)00373-X

(5) Knyazev,V.D.;Bencsura,A.;Dubinsky,I.A.;Gutman,D.; Senkan,S.M.Proc.Combust.Inst.1994,25,817.

(6) Knyazev,V.D.;Dubinsky,I.A.;Slagle,I.R.;Gutman,D. J.Phys.Chem.1994,98,5279.doi:10.1021/j100071a018

(7) Knyazev,V.D.;Dubinsky,I.A.;Slagle,I.R.;Gutman,D. J.Phys.Chem.1994,98,11099.doi:10.1021/j100094a018

(8) Slagle,I.R.;Batt,L.;Gmurczyk,G.W.;Gutman,D.;Tsang,W. J.Phys.Chem.1991,95,7732.doi:10.1021/j100173a034

(9) Bencsura,A.;Knyazev,V.D.;Xing,S.B.;Slagle,I.R.; Gutman,D.Proc.Combust.Inst.1992,24,629.

(10) Zheng,X.B.;Blowers,P.Ind.Eng.Chem.Res.2006,45,530. doi:10.1021/ie0508942

(11)Truong,T.N.J.Chem.Phys.2000,113,4959.

(12) Huynh,L.K.;Ratkiewicz,A.;Truong,T.N.J.Phys.Chem.A 2006,110,473.doi:10.1021/jp051280d

(13)Muszynska,M.;Ratkiewicz,A.;Huynh,L.K.;Truong,T.N. J.Phys.Chem.A 2009,113,8327.doi:10.1021/jp903762x

(14) Bankiewicz,B.;Huynh,L.K.;Ratkiewicz,A.;Truong,T.N.J. Phys.Chem.A 2009,113,1564.doi:10.1021/jp808874j

(15) Zhang,S.W.;Truong,T.N.J.Phys.Chem.A 2003,107,1138. doi:10.1021/jp021265y

(16) Kungwan,N.;Truong,T.N.J.Phys.Chem.A 2005,109,7742. doi:10.1021/jp051799+

(17) Huynh,L.K.;Truong,T.N.Theor.Chem.Acc.2008,120,107. doi:10.1007/s00214-007-0311-9

(18) Hehre,W.J.;Ditchfield,R.;Radom,L.;Pople,J.A.J.Am. Chem.Soc.1970,92,4796.doi:10.1021/ja00719a006

(19) Radom,L.;Hehre,W.J.;Pople,J.A.J.Am.Chem.Soc.1971, 93,289.doi:10.1021/ja00731a001

(20)Wiberg,K.B.;Ochterski,J.W.J.Comput.Chem.1997,18,108.

(21) Gonzalez,C.;Schlegel,H.B.J.Phys.Chem.1990,94,5523. doi:10.1021/j100377a021

(22) Truhlar,D.G.Chem.Phys.Lett.1998,294,45.doi:10.1016/ S0009-2614(98)00866-5

(23) Halkier,A.;Helgaker,T.;Jorgensen,P.J.Chem.Phys.Lett. 1999,302,437.doi:10.1016/S0009-2614(99)00179-7

(24)De Lara-Castells,M.P.;Krems,R.V.;Buchachenko,A.A.J. Chem.Phys.2001,115,10438.doi:10.1063/1.1415078

(25) Huh,S.B.;Lee,J.S.J.Chem.Phys.2003,118,3035.doi: 10.1063/1.1534091

(26) Hwang,R.;Park,Y.C.;Lee,J.S.Theor.Chem.Acc.2006,115, 54.doi:10.1007/s00214-005-0675-7

(27) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03, Revision B.01;Gaussian Inc.:Pittsburgh,PA,2003.

(28)Duncan,W.T.;Bell,R.L.;Truong,T.N.J.Comput.Chem. 1998,19,1039.

(29) Eckart,C.Phys.Rev.1930,35,1303.doi:10.1103/ PhysRev.35.1303

(30)Morganroth,W.E.;Calvert,J.G.J.Am.Chem.Soc.1966,88, 5387.doi:10.1021/ja00975a004

(31) Knyazev,V.D.;Slagle,I.R.J.Phys.Chem.1996,100,5318. doi:10.1021/jp952229k

(32) Kerr,J.A.;Trotman-Dickenson,A.F.J.Chem.Soc.1960,323, 1602.

(33) Gierczak,T.;Gawlowski,J.;Niedzielski,J.React.Kinet.Catal. Lett.1988,36,434.

(34)Tsang,W.J.Am.Chem.Soc.1985,107,2872.doi:10.1021/ ja00296a007

(35) Lin,M.C.;Laidler,K.J.Can.J.Chem.1967,45,1315.

(36) Gang,J.;Pilling,M.J.;Robertson,S.H.J.Chem.Soc.Faraday Trans.1997,93,1481.doi:10.1039/a607566e

(37) Metcalfe,E.L.;Trotman-Dickenson,A.F.J.Chem.Soc.1960, 980,5072.

(38) Slater,D.H.;Collier,S.S.;Calvert,J.G.J.Am.Chem.Soc. 1968,90,268.doi:10.1021/ja01004a010

(39) Douhou,S.;Perrin,D.;Martin,R.J.Chim.Phys.1994,91, 1628.