基于内模原理的变质心弹头控制

李文皓，张珩

(中国科学院力学研究所，北京 100190)

引言

变质心方法通过主动调整质心与气动压心的相对位移，产生气动力矩并用于对飞行姿态的改变，可有效地规避气动外形和气动热问题，且在机动飞行控制能耗方面具有突出优势［1］。近年来，研究者对导弹或弹头的变质心控制方法日趋重视，在变质心方法的动力学、控制律和弹体控制机构设计方面均取得了明确进展［2-4］。

变质心控制方法的主要难点在于:首先，滑块相对运动过程引起了飞行器本体动力学对象的动态变化;其次，姿态动力学的耦合特性增强了运动滑块在各通道间的耦合度;最后，滑块的启动和停止的惯性力矩对弹体系统姿态有明显的抖动影响。

通过对变质心控制动力学的深入研究，对其中的非线性耦合及时变问题提出了包括自适应、动态逆、智能控制等方法，但滑块的惯性力矩问题缺乏有效解决。一般认为，变质心控制稳定的一个基本条件是滑块加/减速时的惯性力矩必须小于气动力矩［5］，因此变质心控制的使用范围一般限制在70 km高度及以下区域的高速飞行体，且滑块质量和加速度受此条件的限制［5］。虽然利用达朗伯原理将滑块布置在弹体的主惯量轴［6］上可大幅削弱反作用力矩，但对姿态可控性范围和工程实现提出了不小挑战。

再入机动弹头一般在高度40 km以下进行变质心调整，可获得较大的机动过载。由于从40 km高度到落地的机动时间短，加之低空的稠密大气对弹头飞行的减速作用和积分效应，对轨迹的改变比较有限。若在高空就进行调整，由于速度高，时间长，对于再入倾角较小的情况，对飞行轨迹和落点的调整作用比较明显。显然，在高空进行变质心调整，弱气动环境下的控制稳定性问题更为突出。

本文主要针对惯性力矩大于甚至远大于气动力矩条件下的变质心弹头的稳定控制问题展开研究，着重讨论变质心控制能达的配平攻角范围，弱气动力环境下的稳定控制方法，以及气动力矩与惯性力矩比值大幅变化时的自适应策略。

1 变质心弹头动力学

1.1 变质心弹头姿态动力学

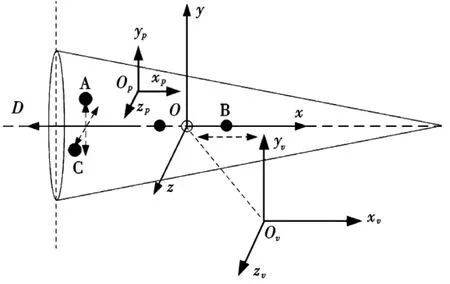
图1 带有3个滑块的质量力矩弹头布局示意图

假设滑块与弹体均为刚体，且相互运动仅为平动，控制滑块的布置如图1所示。轴向滑块B安装于弹体纵轴上，两个径向滑块分别安装于靠尾部的法向(滑块A)平面和侧向(滑块C)平面内。根据多刚体动力学，在弹体坐标系Oxyz、速度坐标系Ov xv yv zv和导轨坐标系Op xp yp zp下建立姿态动力学模型。设弹体总质量为mS，A，B，C滑块的质量分别为mA，mB，mC，装配中点与原质心距离分别为LA，LB，LC，各滑块在导轨坐标系Op xp yp zp下相对装配中心点的移动距离分别为 δA，δB，δC。

姿态动力学方程为:

式中，H为弹头对质心的动量矩;Σ M为作用在弹头上的外力对质心的力矩总矢量，即为空气动力矩与滑块运动引起的惯性力矩之和，Σ M=MF－aero+MF。

将式(1)展开为标量形式则有:

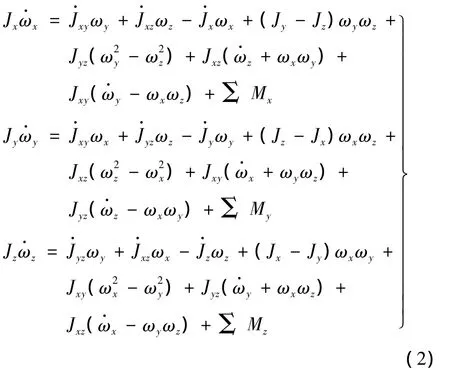
式中，Jx，Jy，Jz为弹头对机体坐标系Oxyz各轴的转动惯量;Jxy，Jyz，Jxz为相应的交差惯性积;ωx，ωy，ωz分别为飞行器相对于地面坐标系的旋转角速度在机体坐标轴上的投影。

惯性力矩MF包括相对惯性力矩MFr，哥氏力矩MFg和陀螺力矩MFt。文献［7］的数值仿真表明，对于三轴受控的飞行器，MFg和MFt的影响可基本忽略，高空段MFr过大会导致控制失稳。因此，本文主要针对MFr设计控制器，相对惯性力矩MFr=［MFx

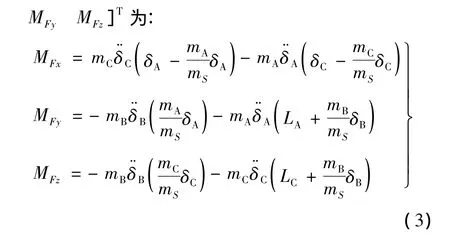
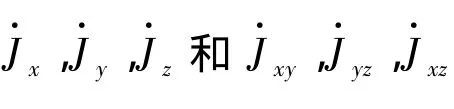
考察总力矩矢量 Σ M=MF－aero+MF，其中MFr为瞬时力矩，仅在滑块加减速运动时存在，为干扰力矩;MF－aero为持续力矩，只要质心偏移即存在，为控制力矩。当MFr≫MF－aero时，控制力矩远小于干扰力矩，使得反馈信息中主要反馈的是由于干扰力矩MFr所产生的姿态角变化，导致反馈失效，引起弹体姿控的不稳定。

1.2 变质心配平攻角能控范围分析

以静稳定弹头为分析对象，考察纵向通道，假设滚转角φ和侧滑角均为零，在存在攻角α时，变质心弹头的气动力矩示意如图2所示。

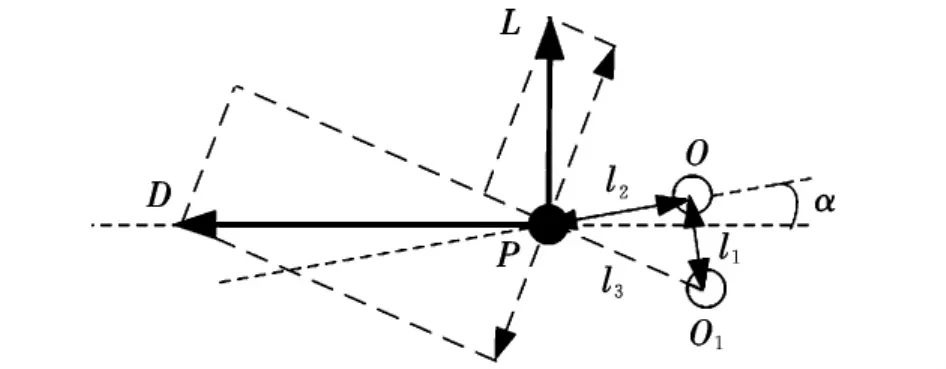
图2 变质心弹头飞行所受气动力矩示意图

气动力矩表达式为:

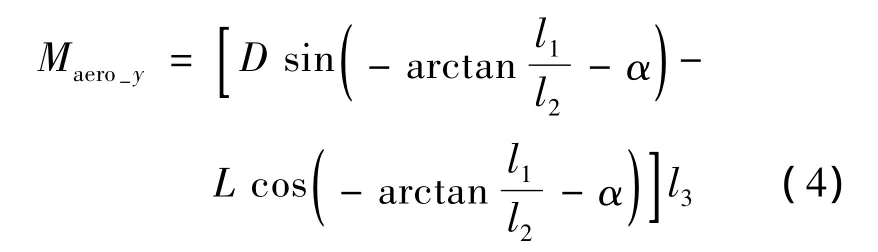
式中，L，D为气动升力和阻力，与飞行攻角α、侧滑角β和马赫数Ma相关;l1为径向质心偏移量;l2为新质心在机体几何体轴上的投影位置到压心的距离，得到:

式中，α 为需求的配平攻角;δA－max，δB－max分别为径向和轴向上滑块可滑动距离。为保证静稳定裕度，一般会设计l2≥llimit。由式(7)可知，当所需的配平攻角越大，对mA和δA－max的需求越高。设径向滑块从零位滑动到δA－max的时间为TA，在不滑动轴向滑块B的条件下，气动力矩与滑块惯性力矩的最大比值为:

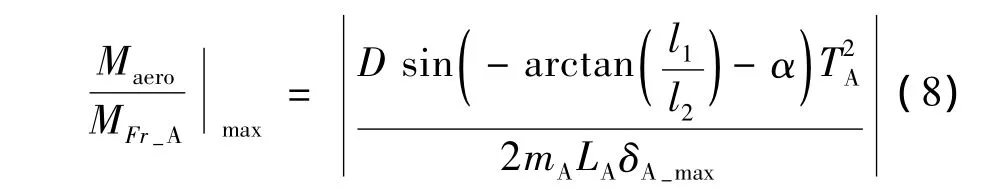
显然，减小滑动调节时间TA，或者增大mA和δA－max会明显增强滑块滑动时的惯性力矩。

2 弱气动环境下变质心姿态稳定控制方法

2.1 弱气动环境下的变质心控制结构

内模原理在20世纪60年代就已经提出来并得到应用，其基本思想是当反馈回路包含外部干扰的动力学模型时，可良好地抵御外部干扰影响，提高反馈精度。前面分析了当MFr≫MF－aero时，姿态控制不稳定的原因是姿态角/角速度反馈中的惯性力矩的影响远高于气动力矩的影响。可以设想，如果能从反馈量中剔除惯性力矩的影响信息，从而达成去惯性力矩化的局部姿态角/角速度反馈条件，则弹体姿态控制的稳定性可以保证。

设计带内模的控制结构如图3所示，分别由P控制器、D角速度反馈、姿态动力学/运动学逆解耦、滑块状态观测器和滑块指令解算模块构成，所需的观测量包括3个姿态角、3个姿态角速度、滑块瞬时位置和滑块瞬时加速度。

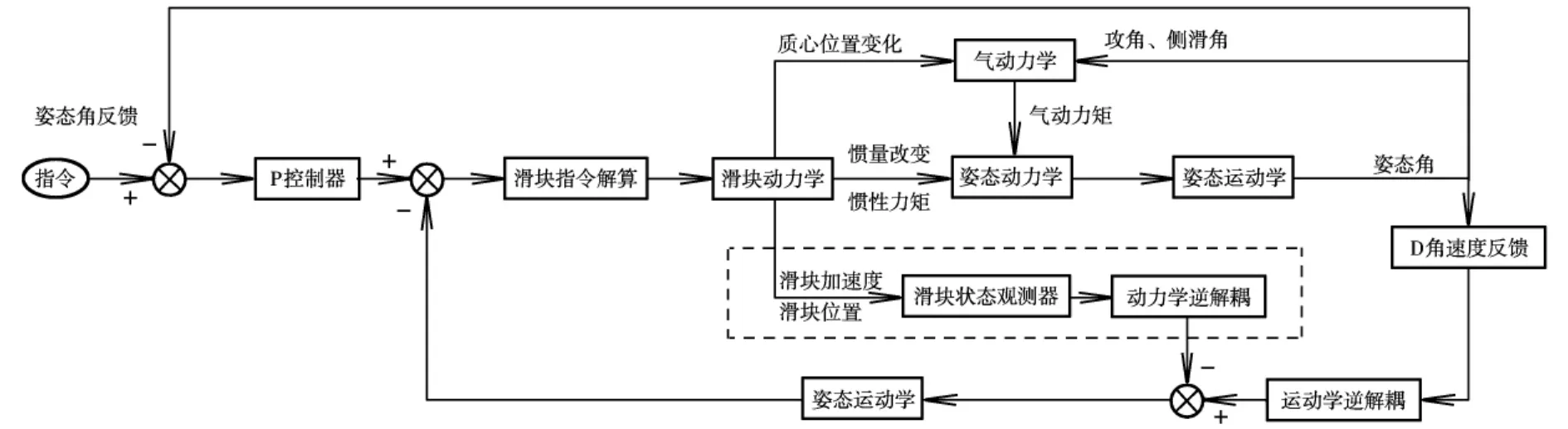
图3 弱气动力条件下的变质心弹头控制结构示意图

2.2 弱气动环境下的变质心控制律

控制器的主结构为PD控制器:

和Mwan－z后，可对解算滑块的控制指令 δA－cmd，δB－cmd和δC－cmd(假设在能控范围内)(由于滚动通道无气动力矩，Mwan－x需使用其他机构实现)。

(1)根据配平攻角能达条件式(7)，确定轴向滑块的位置:

(2)确定轴向滑块位置后，以式(7)取等式可获得 δA－cmd;

(3)同理可获得 δC－cmd。

3 仿真算例

假设某弹头的参数如下:弹体总质量mS为400 kg;弹头底部直径为0.65 m;径向控制滑块质量mA为10 kg;A滑块到质心距离LA为0.62m;可滑动距离δA=±0.3 m;轴向控制滑块质量mB为150 kg(战斗部滑动);B滑块到质心距离LB为－0.1m;可滑动距离δB=±0.1 m;压心到质心的距离为0.05 m;弹体的三轴转动惯量分别为Jx=6 kg·m2，Jy=Jz=110 kg·m2;Jxy，Jyz，Jxz均为零，弹头对应 3°攻角的升阻比为0.17。考虑由伺服机构和滑块构成的变质心闭环系统为良好受控的系统，闭环系统的外部传递函数体现为一阶系统:

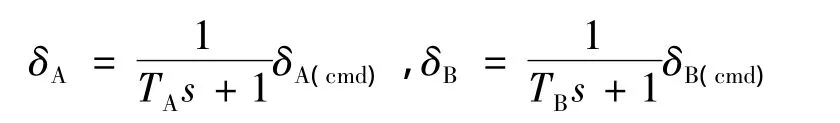
仿真算例中，TA=0.1;TB=1;大气密度模型采用美国1976大气模型;弹头飞行速度取7.3 km/s;高空段阻力系数为2。仿真结果如图4～图6和表1所示。

图4为当指令攻角为3°，分别在高度为110 km，100 km，90 km，80 km和70 km下的攻角控制效果。由图可知，控制稳定性得到了保证，随着高度的降低，上升时间和调整时间缩短，超调量减小。

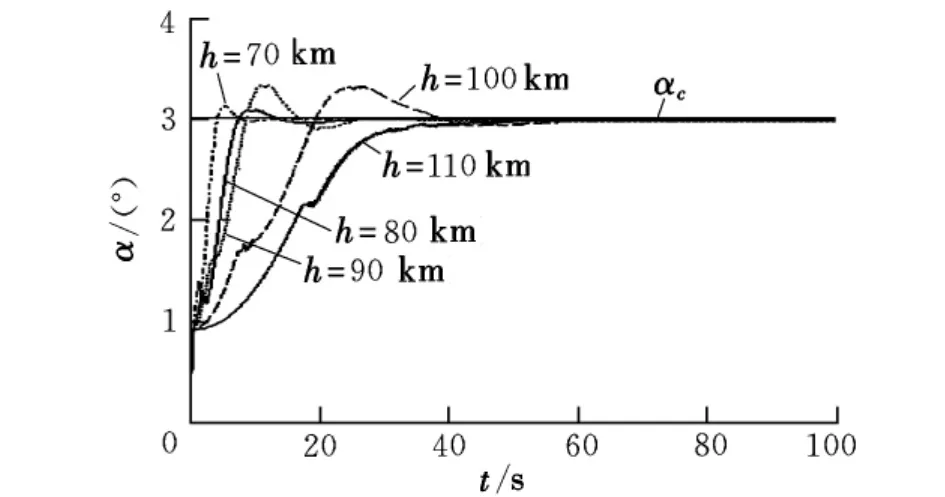
图4 变质心弹头攻角控制效果

图5为当指令攻角为3°，分别在高度为110 km，100 km，90 km，80 km和70 km下攻角控制对应的滑块运动情况。可以看出，高度下降越低，滑块调整至平衡状态所需的时间越短，当气动力远远小于反作用惯性力时，滑块的滑动有微幅快速振荡的趋势。

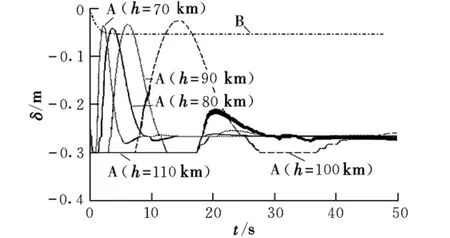
图5 变质心弹头姿态控制的滑块情况

图6为在不同高度下进行变质心控制时的相对惯性力矩与气动力矩的大小比值的变化情况。可以看出，在未达到期望攻角前，由于滑块滑动，其相对惯性力矩远高于气动力矩，有数量级上的差别，说明本文的方法有效地克服了相对惯性力矩强于气动力矩时的控制稳定性问题。

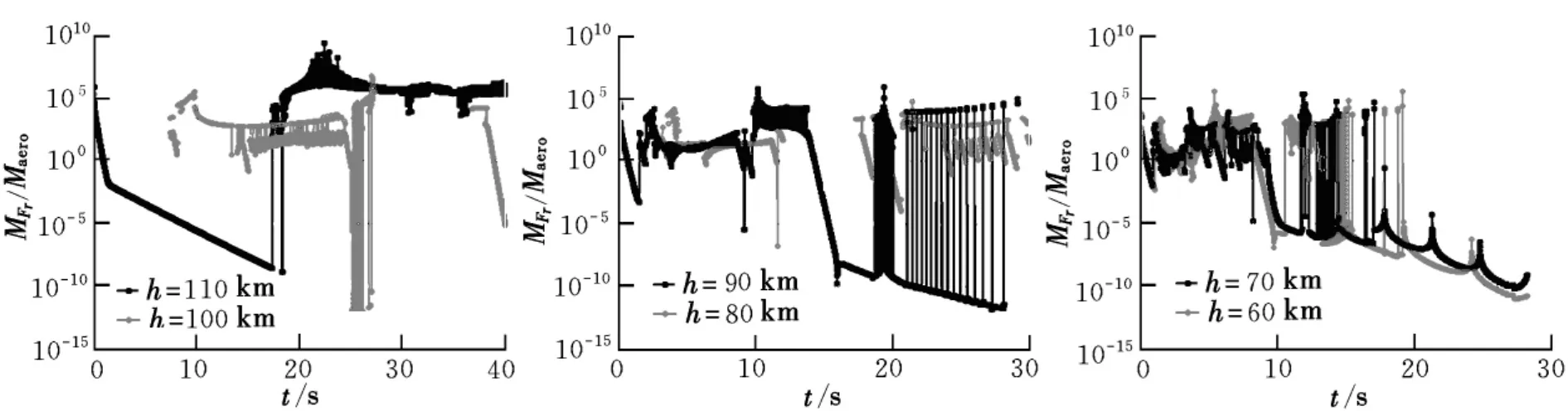
图6 相对惯性力矩与气动力矩的比值变化

表1为不同高度下的变质心姿态控制效果数据表，其中以30 s内时间平均下的惯性力矩与气动力矩的比值作为效果说明。

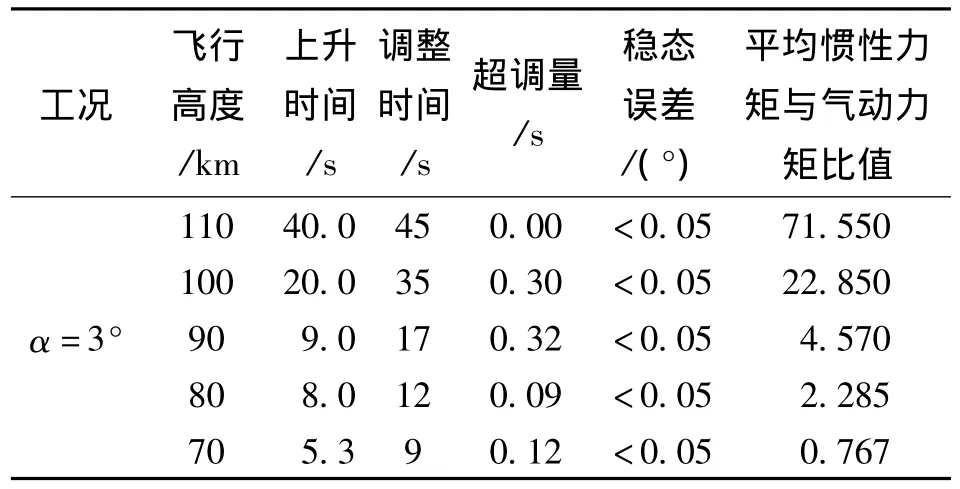
表1 变质心弹头姿态控制效果

从图4～图6和表1可以看出，本文所提出的方法可有效地克服反作用惯性力矩的影响，仿真结果证实了该方法在惯性力矩高于气动力矩1～50倍的条件下仍可保持控制的稳定性。

4 结论

本文重点针对弱气动环境下的弹头变质心稳定控制方法展开了研究，得出了以下结论:

(1)当要求变质心控制可产生可观的配平攻角时，需要配置较大质量的径向滑块并限制静稳定弹体压心到质心距离。

(2)利用滑块状态观测器达成去惯性力矩化的局部角速度反馈是可行的，仿真结果证实了该方法在惯性力矩高于气动力矩数十倍时的控制稳定性。

(3)本文方法所述的弱气动力条件属于相对条件，而并非仅可使用于高空飞行器的变质心控制。采用本文的控制方法，可配置更重的滑块和更高的滑动加速度，这对于提高变质心控制的动态性和增大可配平攻角范围有一定益处。

滑块状态可测条件在工程上是易实现的，需要注意的是，文中假设对滑块状态的测量没有误差，当相对惯性力矩高于气动力矩数个数量级以上时，测量的误差和噪声对系统控制稳定性和精度影响不可避免，不过误差问题并不影响工程上以内模原理思路对相对惯性力矩影响进行消减的有效性。

［1］ Menon P K，Sweriduk G D，Ohlmeyer E J，et al.Integrated with guidance and control ofmoving-mass actuated kinetic warheads［J］.Journal of Guidance，Control，and Dynamics 2004，27(1):118-126.

［2］ Robinett R D，Sturgis B R，Kerr SA.Movingmass trim control for aerospace vehicles［J］.Journal of Guidance，Control，and Dynamics，1996，19(5):1064-1070.

［3］ Petsopoulos Thomas，Regan Frank J.Moving mass roll control system for fix-tirm reentry vehicle［J］.Journal of Spacecraft and Rockets，1996，33(1):54-60.

［4］ 周凤岐，崔利明，周军.弹道式导弹弹头变质心机动控制［J］.宇航学报，2000，21(s1):107-110.

［5］ 郭庆，杨明，王子才.质量矩导弹变质心姿态控制规律研究［J］.控制与决策，2008，23(1):19-24.

［6］ 高长生，荆武兴，李瑞康.提高变质心飞行器可操纵性的方法研究［J］.宇航学报，2008，29(6):1773-1777.

［7］ 高长生.变质心再入飞行器动力学、控制与制导问题研究［D］.哈尔滨:哈尔滨工业大学，2007.