LS-SVM和RBF神经网络模型在降雨预测中的应用
计亚丽,贾克力,李畅游,吴 用,杨 芳,尹琳琳
(内蒙古农业大学 水利与土木建筑工程学院,呼和浩特 010018)
1 引言
降水的形成受到海陆位置、地形、气压带、风带、季风、气旋、洋流、下垫面及人类活动的因素的影响,是一个非常复杂的非线性系统[1]。混沌理论(Chaos Theory)是确定性和内在随机性的一体,揭示了系统运动中有序与无序间相互转化的辩证关系。目前,在水科学领域,混沌理论主要应用在水文时间序列性质的判定和非线性预测模型上[2-5]。为了在高维空间中恢复混沌吸引子,Takens提出了嵌入定理和相空间重构的理论,研究者们在此基础上提出了诸多具有混沌特性的水文时间序列预测模型。其中,最小二乘支持向量机(Least Squares Support Vector Machine,LS-SVM)是在支持向量机的基础上采用二次损失函数的一种改进算法,利用等式约束取代支持向量机的不等式约束。LS-SVM把支持向量机的训练转化为线性方程组的求解,避免了求解二次规划问题,降低了计算过程的复杂度,极大地提高了训练速率,在非线性预测方面和模式识别领域的应用日渐广泛。径向基函数(Radial Basis Function,RBF)神经网络预测模型是一个具有输入层、隐含层、输出层的3层网络结构的前馈型人工神经网络预测模型,具有较强的非线性预测能力[6]。本文依据相空间重构理论对乌尔逊河流域的月降雨时间序列进行混沌性判断,然后使用上述两种混沌时间序列预测模型对乌尔逊河流域的月降雨时间序列进行比较研究。
2 相空间重构及混沌特性识别
2.1 相空间重构
相空间重构是水文现象混沌性识别和非线性预测的前提。相空间重构目的在于刻画出水文系统的混沌吸引子的关联度,揭示传统方法无法展示的水文时间序列变化规律。
按照Takens定理[7],采用延迟坐标法,对混沌时间序列{x1,x2,x3,…,xN}进行相空间重构:

其中Yi向量序列的长度为M=N-(m-1)τ,τ为延迟时间,m为嵌入维数。在相空间重构时,关键在于确定延迟时间τ和嵌入维数m的确定,嵌入维数m应符合m≥2D+1(D为吸引子维数)。
2.2 延迟时间的确定和嵌入维数选取
对于延迟时间τ的选择,目前有很多方法,最常用的有自相关函数法、互信息法和广义相关积分法。由于自相关函数法计算简单,对数据量的要求不大,因此使用最为广泛。
自相关函数法延迟时间τ计算公式为:

式中 rτ为滞时τ时的自相关系数值;x1,x2, …,xN为月降雨时间序列,x軃为时间序列均值。
对于嵌入维数的确定,目前亦有很多方法,其中饱和关联维数法(简称C-P法)由于概念明确、直观而备受研究者偏爱。
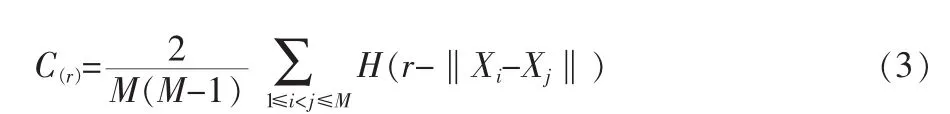
式中 Xi,Xj为重构状态空间中的相点;M为重建后的状态空间数据点的数目, 即M=N-(m-1)τ;m为状态空间嵌入维数;r为以Xi为中心的m嵌入空间中的球体的半径;H为Heaviside函数,是一个单位阶跃函数,即:x≤0时,H(x)=0,x>0时,H(x)=1;‖Xi-Xj‖为欧氏距离;C(r)为关联积分,即所有相空间的点对中,距离小于r的数目在所有相点中所占的比例。
2.3 混沌特性识别
水文时间序列的混沌特性识别方法主要有饱和关联维数法、最大Lyapunov指数法、Kolmogorov熵法等。主要使用动力系统在整个吸引子或无穷长的轨道上平均后得到的特征量[4]。使用Lyapunov指数法判断非线性复杂动力系统是否具有混沌特性[8],必须满足:①至少存在一个正的Lyapunov指数;②至少有一个Lyapunov指数等于0;③Lyapunov指数之和为负[7]。最大Lyapunov指数的计算公式为:

3 预测模型
3.1 最小二乘支持向量机预测模型[11-12]
设混沌时间序列经重构后的M个输入输出数据对为[Xi(n),Yi(n)],Xi(t)∈Rm,yi(t)∈R,i=1,2,…M。
(1)根据相空间重构理论计算出最小嵌入维数m和最佳延迟时间τ,重构相空间。本文采用自相关系数法选取延迟时间τ,采用饱和关联维数法中常用C-P算法确定最小嵌入维数m;
(2)构造样本数据对:

式中 Xi(i=1,2,…,M)为预测输入数据;yi(i=1,2,…,M)为其所对应的输出数据。
(3)对于已给定的混沌时间序列训练样本数据集,(Xi,yi),i=1,2,…,M,可利用高维空间中的线性函数来拟合样本。

非线性映射准(xi)把时间序列数据集从输入空间映射到特征空间,是为了将输入空间的非线性拟合问题转化为高维特征空间中的线性拟合问题,并且把相应的预测问题转化为优化问题,LS-SVM的优化目标函数为:
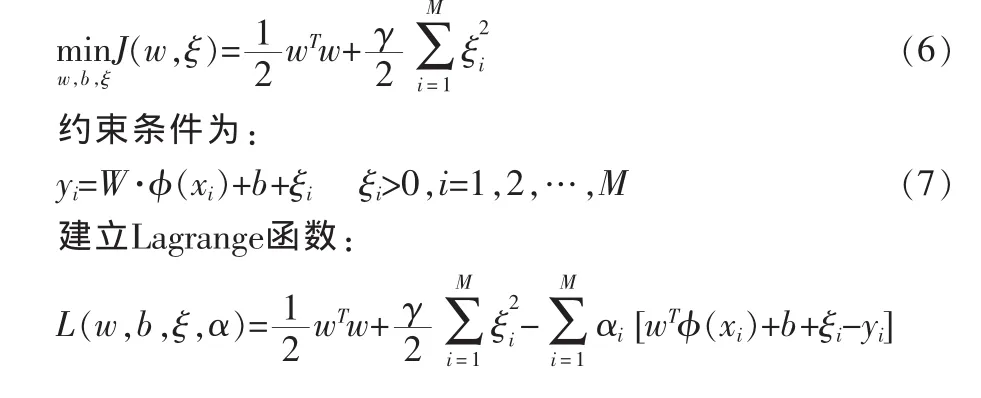

用最小二乘法求出系数αi和常值偏差b,得出混沌时间序列LS-SVM预测模型:

3.2 径向基函数神经网络预测模型[6,9]
RBF主要是基于神经网络的函数非线性逼近功能对降雨时间序列进行分析预测的。在RBF神经网络中,隐含层神经元通过基函数执行一种非线性变化,将输入空间映射到一个新的特征空间,输出层神经元则在这个新的特征空间中实现数据的线性加权组合。RBF神经网络预测模型中使用的基函数仍然是径向基核函数,并且其径向基核函数的中心向量被定义为网络输入层到连接层的权向量[13-14]。对于任意输入向量X∈RN,RN为输入样本集,则隐含层单元的输出为:

式中 Ri(x)为隐含层第i个单元的输出;X为N维输入向量;Ci为隐含层第i个单元径向基核函数的中心点;σi为第i个隐含层神经元的归一化参数;m为隐含层神经元数。
使用RBF神经网络模型进行预测,需要通过学习和训练来确定径向基核函数的中心点Ci,σi,和网络权值等参数,一般按如下步骤进行:
(1)采用K-means聚类方法对训练样本是输入量进行聚类,找出聚类中心Ci和σi参数;
(2)在确定了Ci和σi后,RBF神经网络预测模型从输入到输出就成了一个线性方程组:
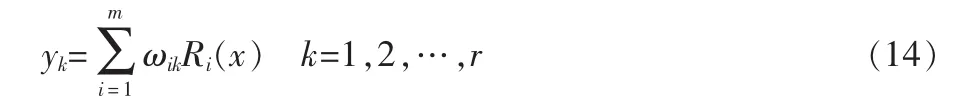
式中 r为输出神经元数;ωik为网络权值。
此时,可以通过最小二乘法来求解网络的权值ωik。
4 预测模型在乌尔逊河流域月降雨中的应用
4.1 基本资料
乌尔逊河流域是呼伦湖流域的子流域,流域面积5980.7km2,位于内蒙古东北部,流域内主要是平坦草原,降雨主要被植被截留和土壤吸收,近年来水量有逐渐减小的趋势,降雨对其有很大影响。
本文主要研究乌尔逊河流域坤都冷水文站1961~2007年的实测月降雨资料,时间序列长度为564个,满足混沌特性分析所需要的时间序列长度。
4.2 延迟时间和嵌入维数的确定及混沌特性的识别
4.2.1 采用自相关函数确定延迟时间
一般情况下,当自相关函数随滞时衰减明显时,延迟时间取自相关函数第1次通过零点时所对应的滞时。当滞时很大自相关函数才趋于零时,延迟时间τ取自相关函数第1次小于时所对应的滞时[6,10]。本文取自相关函数第1次通过零点时所对应的滞时为延迟时间τ。得出乌尔逊河流域月降雨时间序列的最佳延迟时间为τ=2。
4.2.2 确定嵌入维数
确定嵌入维数时,使嵌入维数m=2,3,4…,以1为变幅逐渐增加,绘制lnC(r)~lnr关系图,如果存在无标度区,即直线段,则表明时间序列样本存在混沌特性,且直线段的斜率,就是关联维数D(m)[15-16]。 借助matlab工具进行计算。 图1是乌尔逊河流域月降雨时间序列时间序列的lnC(r)~lnr关系图。图2可以看出,随嵌入维数m的增大,关联维数D(m)趋于稳定,当m≥8时,关联维数出现饱和D=3.1119。符合Takens定理的m≥2D+1条件。由此可见,乌尔逊河流域月降雨时间序列具有混沌特性,同时,使用最大Lyapunov指数法,由公式(4)计算,得到最大Lyapunov指数为0.0782。最大Lyapunov指数大于0,表明具有混沌特性[17-19]。

图1 lnC(r)~lnr关系图

图2 D~m关系图
4.3 月降雨预测
由相空间重构和混沌特性识别可知,乌尔逊河流域月降雨时间序列具有混沌特性,因此,使用LS-SVM预测模型和RBF神经网络预测模型对乌尔逊河流域月降雨混沌时间序列进行模拟和预测。利用前552个数据作为训练数据,后12个数据作为拟合数据,使用MATLAB的LS-SVM工具箱对LS-SVM预测模型进行学习,在拟合、预测精度目标控制下进行优选,最后确定模型参数为γ=10,σ=0.458;使用DPS(DPS9.50)数据处理系统中的RBF神经网络预测模型进行网络学习[6],并依据误差变化过程确定出合理的网络结构,最终确定出乌尔逊河月降雨时间序列的RBF神经网络预测模型的输入层节点数为8,隐含层节点数为6,输出层节点数为1。
表1为2007年乌尔逊河流域月降雨时间序列LS-SVM和RBF神经网络预测模型的预报结果。

表1 LS-SVM和RBF神经网络模型预测结果比较
5 结语
(1)LS-SVM的混沌时间序列预测模型在水文系统的时间序列预测方面还没有完全成熟,处于试验探索阶段。根据混沌时间序列固有的确定性和非线性,LS-SVM能够把输入向量映射到高维特征空间中来提取数据之间的信息。利用混沌系统的相空间重构理论,建立LS-SVM的混沌时间序列预测模型。但是应用在年降雨量不足300mm,且降雨主要集中在7、8月份的干旱、半干旱地区,其预测精度还不能达到满意的程度,有待进一步研究。
(2)RBF神经网络预测模型虽然在DSP(9.50)数据处理系统中已经能够应用,并能够进行简单快捷的运算,在如降雨量较小的1、2月份及11、12月份,拟合误差较大,有待进一步改进。
(3)有待建立适于干旱半干旱地区的简便、训练速度快、拟合精度高的降雨时间序列预测模型。
[1]陈超君,倪长健.攀西地区月降水时序非线性特性分析[J].高原山地气象研究,2011,31(2): 26-30.
[2]于国荣,夏自强.混沌时间序列支持向量机模型及其在径流预测中应用[J].水科学进展,2008,19(1):116-122.
[3]李红霞,许士国,范垂仁.月径流序列的混沌特征识别及Volterra自适应预测法的应用[J].水利学报,2007,38(6):760-766.
[4]Sivakumar B.Chaos theory in geophysics:past, present and future[J].Chaos, Solitons and Fractals,2004,19(22):441-462.
[5]李红霞,许士国,徐向舟,等.混沌理论在水文领域中的研究现状及展望[J].水文,2007,27(6):1-5.
[6]唐启义.DPS数据处理系统实验设计、统计分析及数据挖掘[M].北京:科学出版社,2010.
[7]Taken S F.Detecting strang attractors in turbulence [J].Lecture Notes in Mathematics,1981,898:366-381.
[8]吕金虎,陆君安,陈士华.混沌时间序列分析及其应用[M].武汉:武汉大学出版社,2002.
[9]任磊,岳春芳,何训江.RBF神经网络模型在金沟河流域径流预测中的应用[J].水资源与水工程学报,2011,22(1):94-97.
[10]黄如国,苪孝芳.流域降雨径流时间序列的混沌识别及其预测研究进展[J].水科学进展,2004,15(2):255-260.
[11]罗伟,习华勇.基于最小二乘支持向量机的降雨量预测[J].人民长江,2008,39(19): 29-31.
[12]罗芳琼,吴建生,金龙.基于最小二乘支持向量机集成的降水预报模型[J].热带气象学报,2011,27(4):577-584.
[13]张俊艳,韩文秀.基于RBF神经网络的城市需水量预测研究[J].内蒙古农业大学学报,2006,27(2):90-92.
[14]农吉夫,金龙.基于MATLAB的主成分RBF神经网络降水预报模型[J].热带气象学报,2008,24(6): 713-717.
[15]吴丽娜,黄领梅,沈冰,等.月径流序列混沌特性识别及预测[J].水资源与水工程学报,2010,21(5):28-30.
[16]路剑飞,陈子桑.月降雨序列的混沌判定的合理性分析[J].水电能源科学,2011,29(3): 9-13.
[17]马细霞,穆浩泽.基于混沌分析的月径流序列耦合预测模型及其应用[J].水力发电学报,2010,29(6):41-46.
[18]郁俊莉,王其文.Lyapunov指数混沌特性判定研究[J].武汉理工大学学报,2004,20(2):90-92.
[19]陈继光.基于Lyapunov指数的观测数据短期预测[J].武汉理工大学学报,2001(9):64-67.

