大跨度拱桥弹性动力失稳的简化计算

徐 艳，胡世德

（同济大学 土木工程防灾国家重点实验室，上海200092）

近20年来，随着越来越多大跨度拱桥的相继建成，促进了各地交通经济的发展，其中更有为数不少的大跨度拱桥因其优美的外形成为城市的地标［1］；但另一方面，全球接连发生的几次大地震却表明，震中都位于城市附近，重灾区往往是人口聚集的城市，从而引发对位于城市交通枢纽节点上的许多城市桥梁的抗震性能的特别关注［2－3］。中国已故桥梁专家李国豪先生曾在《桥梁结构的稳定与振动》一书中指出：桥梁结构的稳定性是关系其安全与经济的主要问题之一，它与强度问题具有同等重要的意义［4］。众所周知，其中又以拱桥的稳定问题最为突出。

早期的文献研究表明［5－7］：当结构承受的静载相对较大时，振动分析时就不能忽略失稳因素，此时动力失稳很可能就是结构在振动过程中突发的一种破坏模式。近年来，结构的动力稳定研究取得了很大的进展：文献［8］基于经典动力稳定理论，采用Budiansky and Hutchinson准则针对两端简支的薄壁柱提出了在面内脉冲荷载作用下的临界动力失稳荷载求解的有限元方法；文献［9］针对钢储油罐在水平地震荷载作用下进行了动力失稳的有限元分析，提出了弹性动力失稳的临界峰值加速度PGA；文献［10］为了研究多层钢框架结构在地震作用下的动力稳定性能，对其立柱进行了足尺的单向和循环荷载试验，试验结果以及计算分析表明这种钢立柱在地震荷载作用下会发生多次的非弹性屈曲，但最终仍能抵抗重力荷载；另外，在桥梁抗风领域，风致动力失稳也是一个重要的研究方向，尤其是针对大跨度跨江跨海大桥［11－13］；但在桥梁抗震领域，尤其是稳定问题突出的大跨度拱桥，针对地震引起的拱结构的稳定问题的研究相对比较少见。

鉴于以拱肋为主要承重受压构件的拱桥是众多桥型中稳定问题最为突出的桥型，且随着跨径的增大日益突出，作者曾以钢管混凝土拱桥为工程背景，首次从稳定的角度研究了钢管混凝土拱桥的抗震性能，提出了动力第一类稳定和第二类稳定的概念，并发展了相应的计算方法［14］。其中动力第一类稳定问题本质上为弹性动力屈曲问题，通过作者提出的动态特征值方法进行研究；后者本质上是动力极值问题，根据B－R失稳准则，结合动态增量法进行研究。由于涉及到时间参数，这两种方法都需要以时间积分数值计算为基础，尤其是后者还需要结合材料的非线性参数以及不确定的初始缺陷进行迭代求解，计算相当耗时［15］。另外，随着跨度的增大，拱结构形式的复杂化，模型的单元和节点数也越来越多，使得计算时间更为冗长。从工程设计和应用的角度考虑，希望能有更为简洁和有效，且能与静力稳定相关联的方法来初步判断拱桥的动力稳定性能，以便及时调整设计方案优化结构稳定性能。

因此，本文将针对基于Liapunov动力稳定性意义的动力第一类稳定问题，首先通过对静力屈曲和动力屈曲在数学上的联系，阐明动力屈曲的本质，并将静力稳定安全系数引入动力第一类稳定的计算过程，提出一种简化的计算方法确定拱桥的动力失稳临界荷载，并以一座实际大跨度拱桥为工程背景进行应用和验证。

1 结构弹性动力失稳的本质

由于时间参数的引入，目前对结构的动力失稳准则一直没有达成一致的判别标准，但在弹性动力失稳的本质上，一般都理解为基于Liapunov动力稳定性意义上的动力屈曲［16］。实际上，这是一个动力分叉概念，对于弹性体系最终归结为判断运动方程一次近似矩阵的特征方程的正负定问题。对于具有式（1）的运动方程的结构体系：

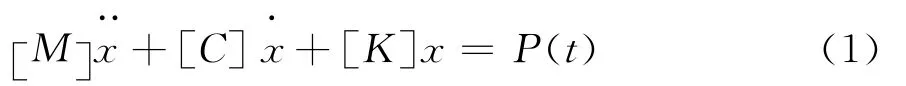
由一般运动稳定性理论可以得到［17］，该方程的一次近似方程的系数矩阵A为：

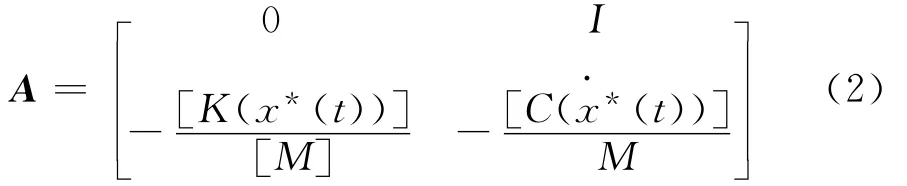
其中特征根的平方λ2，如果忽略阻尼的影响，就是刚度矩阵K＊（K＊是K的三角矩阵）的特征根的负数（－λ2）。但实际结构是有阻尼的，结构阻尼的存在使得一般K＊的特征根不等于λi（λi一般为复数，i＝1，2n），但通过分析可知阻尼的存在（尤其是小阻尼）不会影响特征根的性质。因此，仍然可以通过刚度矩阵的性质来判断一次近似的稳定性，从而判别原运动方程的稳定性。

综上所述，当特征值λi消失时，系统处于稳定与不稳定之间的临界状态，此时ωi＝0，于是动力屈曲在数学上的表现相当于0频率的特征值问题。

式中，如果ωi＝0，并且M是正定的，那么K一定是奇异的。因此我们就将一个动力稳定问题退化到了由式（4）表达的静力准则。

式（4）与文献［18］中曾提出的“结构的振动频率趋于零时，出现动力失稳”这一准则在本质上一致的。此时我们可以忽略质量矩阵的影响，但必须注意，由于非保守力的影响，结构的刚度K一般是不对称的。对于复杂的结构系统，我们可以用这个静力准则简单的判别结构动力稳定性，给出非保守力的临界荷载。

但在确定弹性动力失稳准则这个问题上，曾有学者［19］提出通过二次特征值的方法来分析结构的动力稳定，认为方程（5）的第一特征值是判断动力屈曲的最好指标。

在此基础上得到动力失稳特征方程为：

因此，针对式（4）的判断准则，得到的动力稳定（也称动力屈曲）问题的控制方程为：

即为t时刻求最小特征值α的问题，称α为屈曲系数，λ是输入地震波的比例系数。式中 ［K0］ 为结构的初始弹性刚度矩阵；为由恒载引起的几何刚矩阵；为t时刻动荷载引起的几何刚度矩阵。

2 拱桥弹性动力失稳的研究方法

2.1 动态特征值方法

由于经典的Liapunov意义上的弹性动力稳定性是指离散时间点上的一种动力分叉解，基于这个意义，结构在一个地震动过程中可以具有有限个（与输入地震波的时间长度和时间间隔相关）动力平衡状态，得出在某些时间点或区段上是动力稳定的，而在另一些时间点或区段上却是不稳定的，结构的最终状态有可能是稳定的也有可能是不稳定的结论［17］。

文献［20］正是基于此准则提出了动态特征值法，进行动态的屈曲分析，据此判断在整个地震动过程中是否会发生动力屈曲，图1为动态特征值求解的流程图。

动态特征值方法的初衷就是将结构从0到t时间的振动，经过离散形成n×Δt的时间间隔，使得每一个Δt间隔内，求解式（7），提取n个最小特征值，得到一个反映结构在地震波作用时间内的动态特征值曲线，从该曲线上可以很直观的看到结构在振动的哪一时刻最容易发生动力屈曲，屈曲系数是多少。

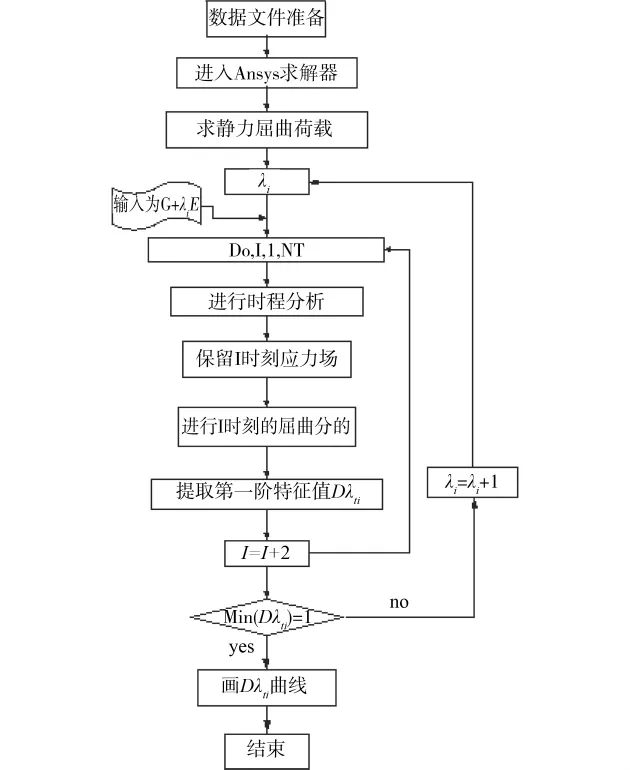
图1 动态特征值法求解流程图

当某一级λ输入，使得式（7）最小特征值α＝1，此时对应的λ即为动力屈曲荷载系数，此时的地震动峰值（g）称为动力屈曲临界荷载，而其他时刻的α表示为当前输入G＋λE（恒载和λ倍的地震波输入）的倍数。值得注意的是：如果λ为0，那么式（7）就是恒载作用下的静力第一类失稳特征方程，α的大小反映了恒载的应力储备。可见，结构的静力屈曲是动力屈曲的一个特殊情况。

但正如前所述，随着拱桥跨度越来越大，结构形式越来越复杂，有限元模型的单元和节点数也越来越多，并且为了得到失稳临界荷载（α＝1）还须对上述λ输入反复迭代，这样使得计算时间太多冗长，直接影响了该方法在实际工程中的应用。因此，一个相对简单却有效的计算方法是非常必要的。

2.2 简化计算方法

经典的稳定理论［4］明确指出，第一类失稳前满足线性假设，在小变形情况下，几何刚度矩阵与应力水平成正比，且仅与单元初始轴力和几何长度位置相关。几何刚度矩阵对单元刚度矩阵的影响主要是由于轴力在单元弯曲时所产生的效应所致，当轴力表现为拉力时，单元的刚度变大，当轴力表现为压力时，单元的刚度变小。而轴力是与外荷载相关的，当外荷载增加到λ倍后，则轴力和几何刚度矩阵也增加λ倍，当λ足够大，使得结构达到随遇平衡状态，此时的λ即为临界荷载比例系数。

由于复杂结构在地震动输入下，结构各组成杆件空间位置和轴力分布并不均匀，因此无法事前较为合理的确定最不利的应力场，但拱桥的主要受压构件为拱肋，纵梁横撑等其他构件均不以受压为主，据此，针对拱桥的这种受力特点，如果我们能事先确定结构的最不利轴力时刻，然后仅对此时刻进行式（7）的屈曲分析，那么就能得到当前输入下（λ倍的地震波）最小的α值。但实际上，我们关心的是需要多大的λ，才能在［0，t］区间的任一时刻使α＝1。

因此，提出如下简化计算方法：

1）首先计算结构在恒载作用下的屈曲系数α，并据此得到临界荷载作用下的轴力N1，可以近似由N1＝αNs（Ns为恒载作用下单元的轴力）得到；

2）然后计算动荷载引起的最不利轴力N2，显然N2＝λNd（Nd为根据原始地震输入下的线性时程计算结果找到的最不利动轴力Nd）；

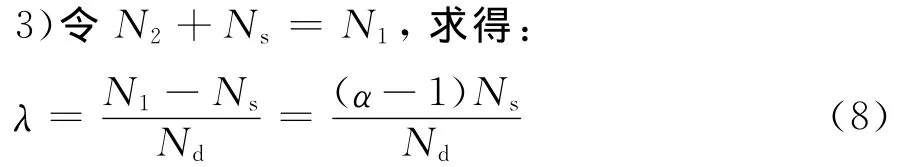
即为弹性动力失稳的最低临界荷载比例系数。

值得注意的是，该方法对于简单受压结构，理论上可以一次快速的找到临界荷载；对复杂的大跨度拱桥，尽管拱肋的轴力分布较为一致，但由于惯性力和阻尼力的存在，各杆件内力时程并不相同，可选取几个关键截面试算几次以确定最小的临界荷载。

自噬不仅参与了正常细胞生长发育、同时也参与了细胞的成熟分化及死亡的调控，自噬活性的改变经常可见于一些肿瘤细胞，影响了肿瘤的发生和发展[4，6]。

3 弹性动力失稳计算方法验证

为验证上述方法的正确性与有效性，本文选取一实际大跨度钢拱桥进行有限元建模，该桥主桥全长750m，为一中承式拱梁组合体系钢拱桥，主跨跨径为550m，拱肋内倾成为提篮拱，矢跨比f／L＝1／5.5，边跨采用跨径各为100m的上承式拱梁结构；桥面宽37m，采用钢加劲板梁结构；两边跨端横梁之间布置强大的水平拉索，以平衡主跨拱肋的水平推力。

采用空间有限元建模，桥梁结构全部模拟为三维梁单元，不考虑支座单元，拱脚在承台处固结，桥面简支，纵向自由；桥面板模拟为一根脊骨梁，主梁和吊杆之间通过刚臂连接，有限元模型如图2所示。

图2 有限元计算模型

根据文献［20］的研究结果，最容易引起结构弹性动力失稳的是地震动的竖向输入，而无论是横向还是纵向输入，对结构的弹性动力失稳临界荷载影响都较小。一方面因为它激起的结构的应力场分布与恒载是不同的，在强烈的地震动作用下，很有可能是局部构件的屈曲发生在前，继而带来整个结构的失稳；另一方面是因为水平地震输入引起拱结构的响应中，弯矩是一个很重要的部分，从本质上属于文献［15］提出的动力稳定极限承载能力的问题。因此，本为以影响最大的竖向输入为例，进行弹性动力失稳临界荷载求解。

1）动态特征值法 首先以原始场地波输入求解，得到动态屈曲系数时程如图3所示，由图可清楚观察地震动输入对结构在整个时间历程中稳定性能的影响，由于地震波的往复交替，这种影响也时而增强时而减弱，最不利的时刻约在11s附近；利用文献［20］在Ansys平台开发的动态特征值求解程序，经过13次循环求解图3所示的动态特征值曲线，当输入地震波比例系数λ＝13.0，在11.16s得到最小屈曲系数α＝1.057，意味着该时刻为动力屈曲的触发点，屈曲模态为面内竖弯，如图4所示。图5为该级荷载输入下拱顶的位移时程，由图可见，拱顶的竖向位移在11s左右表现出了明显的位移瞬时增大的趋势，这也充分说明了t时刻的弹性动力屈曲临界荷载是结构动力失稳的触发点。

图3 动态特征值曲线

图4 屈曲模态（t＝11.16s）

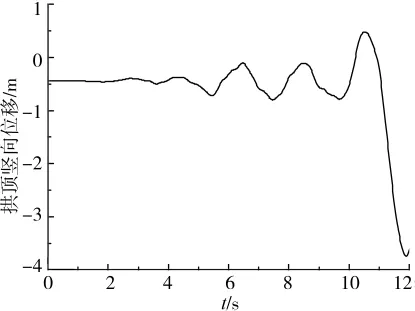
图5 临界荷载作用下拱顶位移时程

2）简化计算方法 如前所述，对复杂的拱桥结构，应用本文简化方法，需要找准能代表结构屈曲的最不利杆件。通常，拱脚单元是受压最大的杆件，但保守起见，我们将拱顶、1／4跨、拱梁结合处处以及拱脚4个截面的轴力时程进行比较，如图6所示。

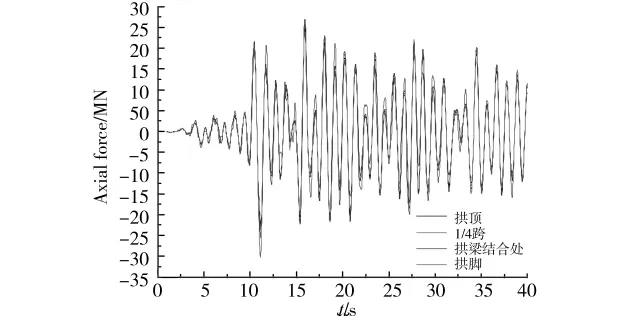
图6 各关键部位线性轴力时程

由图6可知，拱肋各单元的时程曲线基本一致，拱脚的轴力最大，发生在11.12s，其他3个截面的轴力最大值都在11.16s。我们先取拱脚单元为最不利轴力单元，进行计算，计算过程如下：

（1）计算恒载作用下屈曲分析，得到：α＝4.956，屈曲模态与图3一致；

（3）计算由（1）得到的临界荷载作用下的轴力N1＝αNs＝－5.288×108（N）；

（4）拱肋单元最不利动轴力为Nd＝－3.031e7（N），t＝11.12s，N2＝λNd；

（5）令N2＋Ns＝N1，求得：

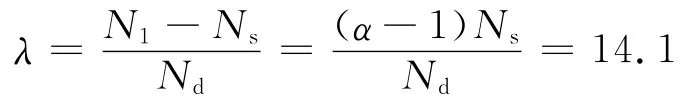
由图3可知，这个计算结果与动态特征值曲线计算得到的结果λ＝13相比，误差为8%，但计算过程和时间却大为简化和减少。

为更进一步说明问题，我们分别取拱顶、1／4跨、拱梁结合处3个单元为最不利单元，重复上述计算，结果列于表1。

表1 动力屈曲临界系数

由表1可见，取用不同代表单元所得结果非常接近，误差均不超过10%。虽然动力屈曲发生的时刻不完全相同，但对于一个动态的时间过程，这一点并不是特别重要，因为如前所述，基于Liapunov动力失稳只是一个激发结构进入不稳定振动的触发点，因此只要最终求得的动力失稳临界系数准确，即达到工程设计和应用的目的。

事实上，如果我们在上述第（3）步对静力屈曲系数α进行迭代，对于本例即从α＝4.956调整恒载比例因子直到α＝1，然后准确得到此时对应的恒载轴力N1而非上述根据初试屈曲系数近似得到的轴力，所得计算结果误差将不超过5%，如表2所示。

表2 动力屈曲临界系数

综上所述，此简化方法不但计算简单，且计算结果准确率高。即便对复杂的结构需进行几次试算，该方法也不需经过循环求解整个时间过程的动态屈曲系数，而仅通过简单的静力计算和线性时程计算结果就能快速确定弹性动力失稳临界荷载。

4 结 论

针对基于Liapunov动力稳定性意义的动力第1类稳定问题，通过得到动力屈曲和静力屈曲在数学上的控制方程，阐明动力屈曲和静力屈曲的本质联系，并将静力稳定安全系数引入动力第1类稳定的计算过程，提出一种更为简化适用的计算方法确定拱桥的动力失稳临界荷载。应用本文方法，通过1座实际大跨度拱桥的第1类动力稳定计算表明：该方法不但计算简单、快速，且准确，误差在5%左右，是比动态特征值法更为有效的第1类动力失稳计算方法。该方法不但可用于大跨度拱桥的弹性动力失稳计算，也可用于其他具有类似稳定问题的桥梁如斜拉桥、悬索桥等索塔结构以及其他土木工程压弯结构的弹性动力稳定分析。

［1］Feng M R.China's major bridges ［C］／／IABSE Workshop Shanghai 2009‘Recent Major Bridges'，May 11－20，Tongji University，Shanghai，China，IABSE Conference Reports，2009，94：1－24.

［2］Fan L C，Zhang F H，XU Y.A Brief introduction on China code for seismic design of urban bridges［C］／／Proceedings of the Second PRC－ US Workshop on Seismic Analysis and Design of Special Bridge，Buffalo，New York，December 3－5，2003，University at Buffalo，MCEER Report，2004：15－22.

［3］Pela L，Aprile A，Benedett A.Seismic assessment of masonry arch bridges［J］.Engineering Structures，2009，31：1777－1788.

［4］李国豪.桥梁结构的稳定与振动［M］.2版.北京：中国铁道出版社，2002.

［5］Gupta A，Krawinkler H.Dynamic P－Delta effects for flexible inelastic steel structures［J］.Journal of Structure Engineering，2000，126（1）：145－154.

［6］ Dionisio B.Instability of buildings subjected to earthquakes ［J］.Journal of Structure Engineering，ASCE，1992，18（8）：2239－2260.

［7］Nakajima A，Kuranishi S，Abe H.Dynamic failure of structures with structural instability ［J］.Structural Engineering and Earthquake Engineering，JSCE，1987，4（2）：351－360.

［8］Teter A.Dynamic multimode buckling of thin－walled columns subjected to in－plane pulse loading［J］.International Journal of Non－Linear Mechanics，2010，45：207－218.

［9］Virella J，Godoy L，Su′arez L.Dynamic buckling of anchored steel tanks subjected to horizontal earthquake excitation［J］.Journal of Constructional Steel Research，2006，62：521－531.

［10］Lamarche C P，Tremblay R.Seismically induced cyclic buckling of steel columns including residual－stress and strain－rate effects［J］.Journal of Constructional Steel Research，2011，67（9）：1401－1410.

［11］Diana G，Rocchi D，Argentini T，et al.Aerodynamic instability of a bridge deck section model：Linear and nonlinear approach to force modeling ［J］.Journal of Wind Engineering and Industrial Aerodynamics，2010，98（6／7）：363－374.

［12］Caracoglia L，Sarkar P P，Haan F L，et al.Comparative and sensitivity study of flutter derivatives of selected bridge deck sections，Part 2：Implications on the aerodynamic stability of long－span bridges［J］.Engineering Structures，2009，31（9）：2194－2202.

［13］Ge Y J，Xiang H F.Computational models and methods for aerodynamic flutter of long－span bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96（10／11）：1912－1924.

［14］徐艳，胡世德.地震作用下钢管混凝土拱桥的动力稳定性［J］.同济大学学报：自然科学版，2007，35（3）：315－319.XU Yan，HU Shide.Dynamic stability of concrete filled steel tubular arch bridge under earthquake［J］.Journal of Tongji University：Natural Science，2007，35（3）：315－319.

［15］徐艳，胡世德.钢管混凝土拱桥的动力稳定极限承载力研究方法［J］.土木工程学报，2006，39（9）：68－73.XU Yan，HU Shide.A study on the dynamic ultimate capacity of CFST arch bridge ［J］.China Civil Engineering Journal，2006，39（9）：68－73.

［16］韩强.弹塑性系统的动力屈曲和分叉［M］.北京：科学出版社，2000.

［17］沈祖炎，叶继红.运动稳定性理论在结构动力分析中的应用［J］.工程力学，1997，14（3）：21－28.SHEN Zuyan，YE Jihong.Structrual dynamic analysis by motion stability theory［J］.Engineering Mechanics，1997，14（3）：21－28.

［18］Auli W，Rammerstofer F G.On the dynamic instability of shell structures－criteria and algorithm，finite element methods for shell structures［M］.Pineridge Press，Swansea，1990.

［19］Montes E H，Martin L.Influence of dynamic movements due to seismic response on the buckling problem of steel structures［J］.Journal of Constructional Steel Research，1998，46（1）：445.

［20］徐艳，胡世德.钢管混凝土拱桥的弹性动力稳定性能研究［J］.地震工程与工程振动，2006，26（4）：162－167.XU Yan，HU Shide.Study on elastic dynamic stability of a CFST arch bridge［J］.Earthquake Engineering and Engineering Vibration，2006，26（4）：162－167.