软土基坑引起下卧隧道隆起的非线性流变

张俊峰，王建华，温锁林

（1.上海交通大学 土木系，上海200240；2.上海隧道工程股份有限公司，上海200082）

近年来在城市建设、市政交通施工中经常会碰到这种地铁隧道上方进行基坑开挖的情况。这种土体开挖引起了基坑周边土体应力场的改变，进而可能引起临近构筑物的不均匀沉降和混凝土开裂等不利影响。同样，地铁隧道的不均匀沉降可造成隧道的直接破坏［1］。因此对于这种越来越多的隧道上方基坑开挖情况，必须在开挖之前对开挖造成的隧道隆起问题事先进行预测和地铁运行安全性评估。

目前进行基坑开挖引起的隧道隆起量预测主要有3类方法：大型有限元数值模拟分析［2－3］、残余应力法［4］以及基于Mindlin理论解推导隧道应力的弹性地基梁方法［5］。大型有限元方法对于基坑整体分析问题比较全面，由于建立了三维模型，分析结果非常详细和直观。但是实际工程中对于初步方案设计、详细施工方案论证等诸多阶段，由于设计目的不同，不可能每个阶段都建立大型有限元模型进行长时分析。残余应力法按分层总和法的思路，根据开挖引起的残余应力场计算了隧道处土体的隆起变形，该方法简便易于理解和使用，但该方法没有考虑隧道抵抗土体隆起的作用。基于Mindlin理论解推导隧道应力的弹性地基梁方法计算了隧道处的应力分布进而按弹性地基梁的方法计算隧道变形，这种方法较好地考虑了隧道的刚度作用，但是没有考虑隧道与周边土体力的相互作用。

根据基坑开挖引起的土体变形具有明显的空间效应和时间效应的特点，根据实际工程设计分析的不同需要，提出了预测隧道隆起的方法。通过采用Boussinesq解和隧道反力Mindlin解，进行土与隧道进行变形耦合相互作用分析，同时考虑软土的非线性流变特点，推导隧道隆起量的计算方法。通过应用该方法，基坑开挖面积对隧道变形的影响进行了分析，并且对上海市重点工程东西通道右转匝道基坑工程进行了隧道变形过程预测。

1 理论分析

2.1 基坑开挖引起的隧道处某点隆起S1

基坑开挖是1种卸载过程，一旦土体被挖除，基坑底部土体的初始应力场将会改变。总的卸载量为开挖土体重量。卸载引起的基坑下方土体自由隆起可采用类似天然地基沉降计算的方法来进行预测，荷载方向为向上，变形为隆起。

采用弹性半空间集中荷载的Boussinesq弹性应力解作为基本解，来分析基坑坑底荷载作用下应力扩散情况。

图1 卸载情况下基坑底部的土体受力情况

基坑底部开挖面的卸载量为式（1），

式中：P0为总的卸载载荷大小；γi为各被开挖土层的土体天然容重；hi各被开挖土层的厚度。

图2 开挖卸载引起的土中应力数值积分计算

对于基坑开挖平面不规则的情况，利用Boussinesq弹性解很难直接得到土体内部卸载产生的应力分布，因此采用了半理论半数值方法进行分析。任意形状的开挖面的卸载被细分为很小面积的矩形均布荷载，通过数值积分的方法利用Boussinesq解得到土体内部任意点产生的隆起应力。

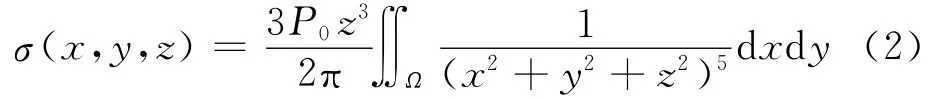
式中，σ（x，y，z）为土体中某点产生的应力；Ω为任意形状的开挖平面面积；P0为卸载大小。

软土地区土体具有沉降变形与时间相关的流变特性。流变特性首先与土的结构有关，无论砂土还是粘土都有一定程度的流变性质。根据文献［6－8］，这种特性可采用开尔文粘滞弹簧模型进行模拟土的流变特性（图3）。

图3 开尔文流变模型

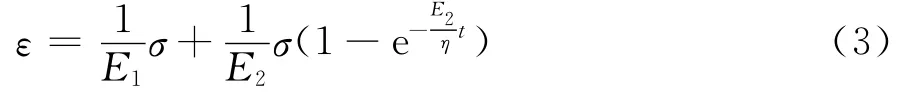
土体的本构模型可通过推导得到式（3），式中：E1、E2为杨氏弹性模量；η为粘滞壶的流变系数。

地基土是比较复杂的材料，一般是成层分布，时常出现夹层或缺失等复杂分布情况。因此，沉降计算结果同实际结果往往相差较大，为了使计算结果接近实测沉降值，引用了经验系数予以修正。这样，根据计算得到的土体隆起应力，得到考虑土体流变特性的地基中任意点的隆起变形。

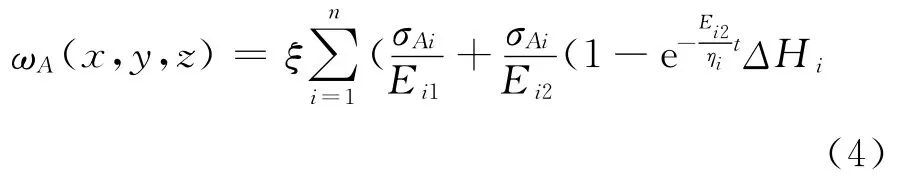
式中ξ为经验修正系数；n为计算点以下变形影响范围内的土层数；Ei1、Ei2为分层土的杨氏弹性模量；ηi为分层土的流变系数；σAi为计算点以下各土层卸载产生的平均应力；ΔHi为计算点以下各土层的厚度。

1.2 隧道土反力引起的地基变形S2

对于土体中隧道来说，隧道横向尺寸远远小于纵向尺寸，隧道的力学特性相当于土体中的地基梁。各段隧道可假设为细化的梁单元。梁单元宽度等于隧道直径。梁单元与土体间的作用力将给土体带来另外的变形。通过采用Mindlin应力基本解得到所有隧道与土体间的作用力引起的土体任意位置的应力。

分析中梁沿隧道纵向轴线被分割成许多矩形单元，任意单元与土体接触面上的土体压力，P1，为大小均匀分布。

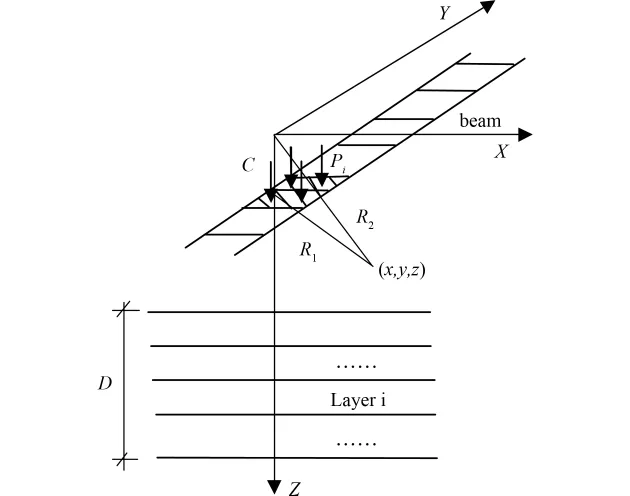
图4 梁单元荷载引起的土体变形分析

土体中任意点（x，y，z）由于梁单元i上的荷载引起的应力大小可通过式（5）得到。

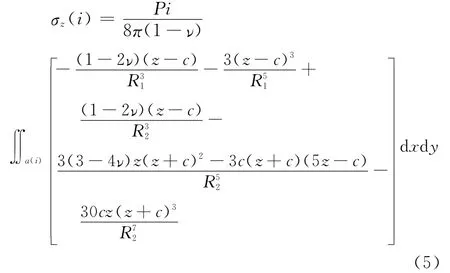
式中：Pi为梁单元i上的荷载；a（i）为单元i面积；z为计算点深度；C为梁深度；v为土体泊松比；R1为计算点到梁单元距离；R2计算点与原点距离。

那么引起的计算点应力通过数值积分得到：

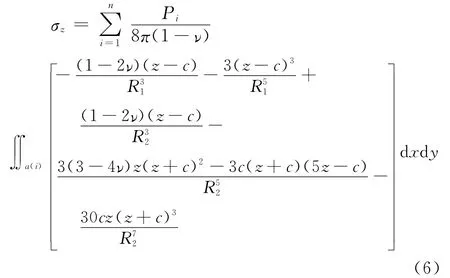
式中n为对计算点产生影响的单元数量。

我们同样可得到流变土体位移表达式（7），

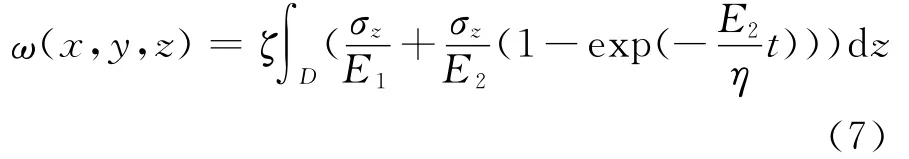
式中D为影响深度；ζ为经验修正系数；σz为计算点以下土体应力；E1、E2为弹性模量；η为流变系数。

1.3 隧道本身的弯曲变形分析

隧道本身由接触土反力引起的弯曲变形可以通过分析连续梁的变形来得到。接触土反力是隧道作用于土体的压力反作用力。隧道也按梁假设，并且假设连续梁足够长，那么可以认为连续梁边界条件为式（8）。

图5 连续梁的变形

由于连续梁的作用荷载为非均匀，直接得到连续梁的变形表达式比较困难。因此采用有限元分析的方法是必要的。连续梁的刚度矩阵为式（9）。

式中：L为连续梁单元的长度；EI为梁单元的抗弯刚度。林永国［9］提供了隧道抗弯刚度计算方法。

从式（11）可得整个连续梁的刚度矩阵 ［K］，那么可得到物理方程式（10），

式中［s］为连续梁的位移向量；F为连续梁与土体的接触压力荷载向量。它们分别可表示为式（11）、（12）。

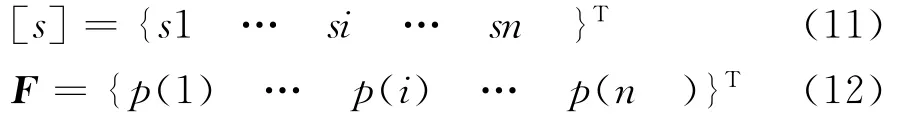
由式（12），连续梁的变形向量可表示为式（13）。

式中［δ］为连续梁的柔度矩阵。

1.4 隧道与土的相互作用耦合分析

土体的变形与连续梁不发生脱离，因此它们的变形可进行耦合分析。

根据公式5，在隧道不存在的情况下由于开挖卸载引起的土体变形向量为：

式中ω1（i）为连续梁各单元处土体位移。

由公式9可得到连续梁压力引起的土体位移向量：

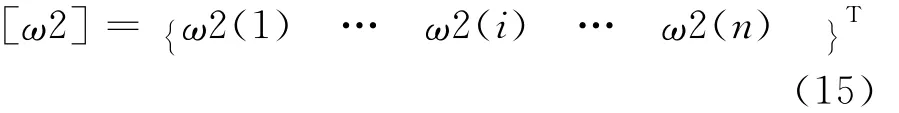
式中ω2（i）连续梁各单元中点处土体的位移。

那么耦合方程可表示为：

通过求解公式18，我们可以得到任意梁单元的位移，也就是我们得到了隧道位移。

2 基坑开挖面积对隧道隆起影响

假设基坑平面为方形，并且边缘平行于隧道轴线。基坑开挖深度为8m，基坑底部距离隧道顶部4.8m。假设开挖面积与穿越隧道的面积之比，跨越面积比r，由1增加到19。

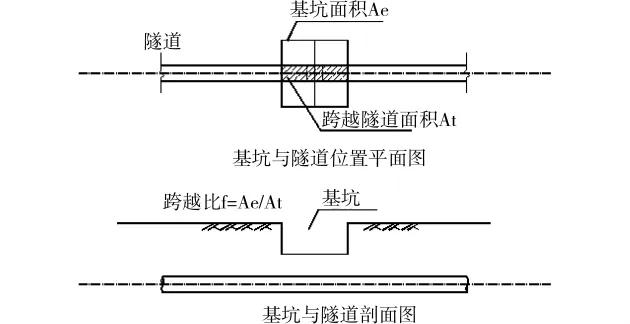
图6 隧道上方基坑开挖平面和剖面图

为了分析方便，假定土体为单一均质土体，E1＝100MPa，E2＝100MPa，η取3 000d·MPa。隧道直径取6.2m，C30混凝土材料，弹性模量取3 0000MPa，隧道管片厚度取0.35m，隧道等效纵向弯曲刚度取668 00MN·m2［9］。

把隧道的变形与基坑跨越面积比的关系绘成图，见图7。

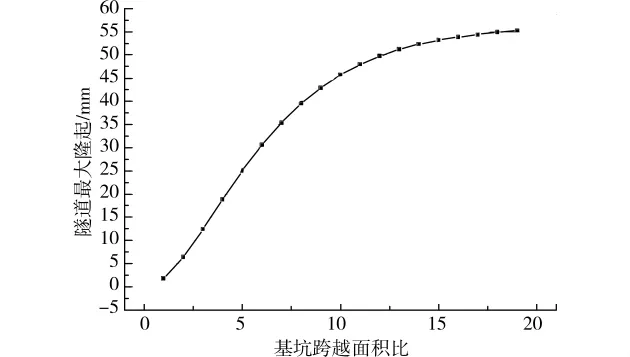
图7 基坑开挖跨越面积比与最大隧道隆起的关系

由图7可知，随着面积的增加，最大的隧道变形并不是线性增长。起始阶段，随着跨越面积比r增加而最大隧道变形快速增加。当跨越面积比r达到10之后，最大的隧道变形增长很小，曲线更加平缓。因此可以认为当跨越面积比达到一定程度后，最大隧道变形基本达到可能的最大变形。

3 工程实例分析

上海市重点工程浦东东西通道穿越地铁工程具有开挖土方量大、穿越次数多、距离地铁隧道近的特点。这里就其中一段匝道基坑工程上方穿越地铁隧道工程进行开挖的隆起变形分析。该基坑开挖深度为6.3m左右，开挖宽度达9.6m，长度大于70.8m。基坑下方地铁隧道的中心深度为11.4m，基坑底部距离隧道顶部仅2m。隧道的开挖基坑以及隧道走向平面图如图8。

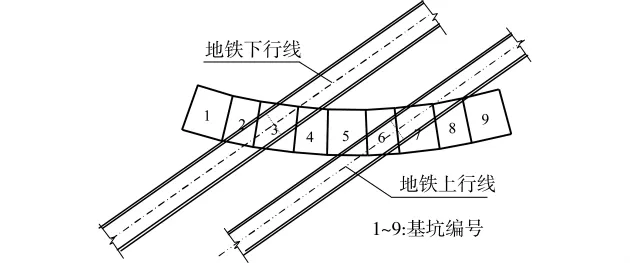
图8 基坑开挖穿越运行地铁隧道的平面图

该工程场地条件比较差，为上海典型的软土，地质条件复杂。根据上海地区经验，弹性模量取为压缩模量的2～3倍。场地工程地质条件见表1。

软土地区土体具有流变的特性，基坑开挖引起的周边建筑物的变形，不仅和其附近开挖的基坑面积大小、而且与距离远近有关，还同开挖方式、时间工况等密切相关。

考虑到地铁的运行安全，地铁相关管理规定对地铁隧道的变形要求极其严格。根据软土具有流变这个特性，为了减小基坑开挖引起的隧道隆起变形，工程中采用了时空效应的开挖方法来尽量减少隧道隆起量。右转匝道整个基坑采用了分块、分层开挖方式进行开挖。整个基坑划分为9块小基坑，每个基坑又按不同的速度分层挖土、浇筑混凝土底板。该项工程自2009年2月11日开始开挖，采用了先两头再中间的方式进行基坑开挖，3月22日浇筑好最后一块基坑顶板，土建开挖工程基本结束。具体开挖情况可见表2。

表1 地基土的物理力学性质指标表

表2 基坑开挖工况进度表

采用残余应力法等方法不能反映时间效应，而实际基坑工程的实测表明基坑开挖引起的变形具有明显地时间效应，因此对于复杂工况下考虑时间因素更为合理。通过对此项工程的开挖采用流变方法计算，得到了图9所示结果。

本工程是上海市重点工程，在基坑施工过程中对地铁隧道进行了全程监测，在整个开挖过程中对隧道隆起采用了电水平自动监测采集记录。实际监测的隧道隆起结果见图9。

当各分块土体被开挖后，隧道开始发生隆起。当开挖到基坑底部并开始浇筑底板后，隧道隆起到达最大值后开始发生减小。隧道隆起量由土体卸载和后续的底板加载共同决定。

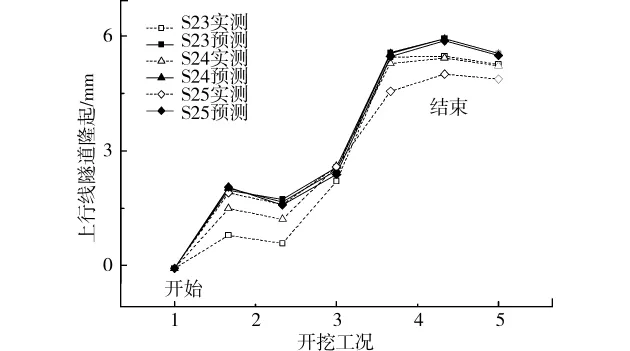
图9 （a） 各施工阶段上行线隧道预测变形与实测变形

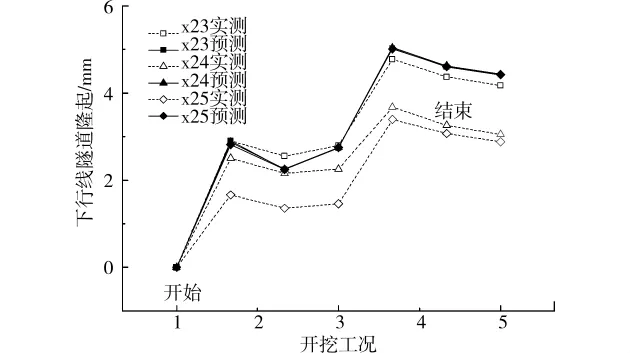
图9 （b） 各施工阶段下行线隧道预测变形与实测变形

上行线预计最大隆起为6.1mm，下行线为5.5mm。而根据现场实测，上行线隧道最大隆起量为5.32mm，下行线隧道最大隆起为4.17mm。虽然预测的结果与实测值具有一定的差别，但是对于总体来说预测的结果还是能反映整个基坑开挖工况的隧道变形变化发展情况，因此采用本文的方法进行基坑开挖引起的隧道隆起预测是可行的。

4 相关结论

根据Boussinesq应力解和Mindlin应力解计算基坑开挖引起的土体应力卸荷增量，考虑隧道刚度后进行了土与隧道变形相互作用耦合分析，同时考虑软土的流变时间效应，得到基坑开挖引起的下卧隧道隆起量的计算方法。通过该方法，分析了基坑开挖性状对下方隧道隆起的影响，得到如下结论：

1）通过引入土的非线性流变模型，能够考虑土体变形的时间特性。

2）使用该方法可知，基坑开挖的跨越面积比r增加，隧道变形增加。当跨越面积比r达到10之后，隧道变形增加很小。

3）通过对实际工程的对比分析，通过对实际工程的对比分析，采用本文方法进行复杂工况下基坑开挖引起的隧道隆起分析，预测的隧道隆起过程与实测值比较接近。

［1］Chang C T，Sun C W，Duann S W，et al.Response of a Taipei Rapid Transit System （TRTS）tunnel to adjacent excavation ［J］.Tunnelling and Underground Space Technology，2001，16：151－158.

［2］戚科骏，王旭东，蒋刚，等.临近地铁隧道的深基坑开挖分析［J］.岩石力学与工程学报，2005，24（Sup）：5485－5489.QI Kejun，WANG Xudong，JIANG Gang，et al.Analysis of deep pit excavation adjacent to tunnel［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（Sup）：5485－5489.

［3］LI Yunpeng，WANG Zhiyin.Study of influence of subway station excavation on existing metro displacement［C］／／Critical Issues in Transportation Systems Planning，Development，and Management，2009，ASCE：3345－3339.

［4］吉茂杰，刘国彬.开挖卸荷引起地铁隧道位移的预测方法［J］.同济大学学报，2001，29（5）：531－535.JI Maojie，LIU Guobin.Prediction method of displacement of subway tunnel due to excavation［J］.Journal of Tongji University，2001，29（5）：531－535.

［5］陈郁，李永盛.基坑开挖卸荷引起下卧隧道隆起的计算方法［J］.地下空间与工程学报，2005，1（1）：91－94.CHEN Yu，LI Yongsheng.Calculation of tunnel heaving due to unloading of pit excavation［J］.Chinese Journal of Underground Space and Engineering，2005，1（1）：91－94.

［6］郑榕明，陆浩亮，孙钧.软土工程中的非线性流变分析［J］.岩土工程学报，1996，18（5）：1－13.ZHENG Rongming，LU Haoliang，SUN Jun.Nonlinear creep analysis for soft soil engineering ［J］.Chinese Journal of Geotechnical Engineering，1996，18（5）：1－13.

［7］王祥秋，陈秋南，王文星.两种地基土非线性流变特性与模型理论研究［J］.湘潭大学自然科学学报，2001，23（2）：106－112.WANG Xiangqiu，CHEN Qiunan，WANG Wenxing.The research of non－linear rheological properties and model theory for two types of foundational soil［J］.Natural Science Journal of iangtan University，2001，23（2）：106－112.

［8］Anders A，Morten L，Poul V L.Evaluation of timedependent behavior of soils［J］.International Journal of Geomechanics.2004，4（3）：137－156.

［9］林永国.地铁隧道纵向变形结构性能研究［D］.上海：同济大学土木工程学院，2001.