考虑结构状态扰动的天然黏土一维压缩模型

朱启银，尹振宇，王建华，夏小和

（上海交通大学 土木工程系海洋岩土研究中心，上海200240）

结构性黏土在中国广泛分布在沿海、沿江地带。随着经济建设的大发展，越来越多的工程建设在这些结构性黏土层之上；结构性黏土由于在天然沉积过程中形成颗粒间胶结和大孔隙结构特点［1－2］，导致压缩变形较大，给地基基础的稳定性带来了很大安全隐患，给工程设计及建设的安全性和经济性提出了很大的挑战。

为了解结构性黏土的压缩变形规律，很多学者针对不同地区（中国如天津［3］、湖南［4］、山东［4］、福建［4］、江苏［5］、上海［6］、广东［6－7］、浙江［8－9］、湖北［10］等；其他国家如英国［1］、芬兰［2］、日本 Ariake［11－12］、墨西哥 Mexico［13］、加拿大 Riguad［14］等）的天然黏土做了大量的一维压缩试验。在理论方面，也有一些能够反应天然黏土结构破坏的弹塑性模型，比较典型的有Hong等［11］提出在双对数坐标上的压缩曲线中，应用场地状态线（FSL）来分析结构性黏土一维压缩特性的本构模型，此模型表达式简单、易用；不过其双对数曲线模型与剑桥模型的半对数曲线概念不太一致。Liu等［15］应用扰动状态概念分析了结构性黏土的重塑土样和原状土样孔隙比的差值，从而建立了能够反映一维条件下结构破坏的理论计算方法。另外，刘维正等［16］亦基于扰动状态概念建立了结构性土的本构模型。尽管这些理论方法可以很好的模拟黏土的压缩特性，但由于模型数学表达相对复杂，参数不能直接量取，不能简便地应用于实际工程。为此，本文以中国天然黏土的一维压缩特性为基础，尝试提出一个使用简单且较易扩展扰动状态模型的一维压缩模拟方法。

本文首先分析了中国12种不同地区的天然黏土一维压缩试验结果，引入“结构比”建立了符合结构性黏土一维压缩特性的简单模拟方法，并且分析了模型参数的确定，以及应用此模型来模拟结构性黏土的一维压缩试验，最后应用扰动状态概念讨论模型对不同扰动状态土的本构模拟推广。

1 结构性黏土压缩试验分析

研究调查了广泛分布在中国不同地区的12种天然黏土的一维压缩试验，土样所取地区分别为大港［3］、汉沽［3］、黄石［4］、青岛［4］、漳州［4］、连云港［5］、上海［6］、珠海［6］、南沙［7］、温州［8］、萧山［9］和武汉［10］（如图1）。因此，本调查囊括了中国较为典型的结构性黏土。从土样的物理性能指标（表1）中可以发现，不同地区结构性黏土的初始含水量、重度、孔隙比、塑限和液限表现出来的差异性较大，含水量变化范围为39.5%～70.5%；初始孔隙比变化范围为1.12～1.85。除青岛、上海和温州黏土含水率值略低于液限值外，其它黏土的含水率值均大于液限值。按照Casagrande塑性图分类（如图2），所调查的黏土包括低塑性无机黏土、高塑性无机黏土、高塑性粉质黏土和砂质黏土。

图3分别给出了这12种天然黏土的原状和重塑土样压缩曲线。所有黏土的压缩曲线有一个共性：原状土压缩曲线位于重塑土之上，具有明显的屈服应力拐点；当应力低于屈服应力时，原状土压缩变形与土结构性无关［15］，土的压缩性很小；当应力大于屈服应力时，孔隙比急剧减小，压缩性显著增大，且大于重塑土的压缩性；当应力继续增大，原状土压缩曲线将趋近于重塑土，这时可以认为结构破坏近乎殆尽。

图1 所调查天然黏土的分布图

图2 土样在塑性图上的分布图

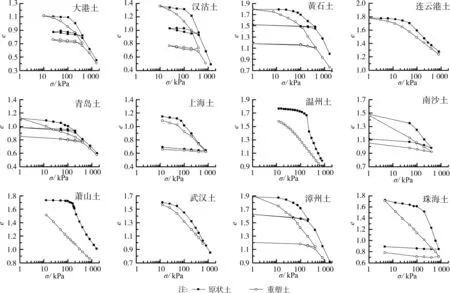
图3 中国12种天然黏土的一维压缩曲线图

表1 中国12种天然黏土的物理性质指标

此压缩共性可由图4来描述。原状土的压缩曲线与重塑土的压缩曲线或其延伸线相交于（σpi0，epi0）；定义重塑土e－ln（σ）曲线斜率为λi；σp0为原状土的屈服应力；σv为当前应力。在σv从σpi0变化到σp0过程中，原状土表现出弹性压缩，此阶段e－ln（σ）曲线斜率为κ；当σv超过σp0，原状土开始产生塑性变形，假设σv增大到图4位置时，对应的原状土塑性孔隙比变化量为Δep。对于重塑土要产生同样大小的Δep，其应力状态需要从σpi0变化到σvi（图4）。

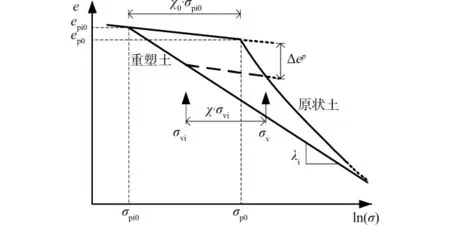
图4 天然黏土原状与重塑土样一维压缩关系

2 结构性黏土一维压缩模型

2.1 一维压缩模型

由图4可定义反映结构性黏土和重塑土关系的结构性变量χ0，表达式如式（1），

式中：χ0即为“结构比”参数χ的初始值。其物理意思近似于土的灵敏度。如图4所示，当产生塑性应变Δep时，χ从χ0值减小，表达如式（2）。

按照上述“结构比”定义，可以得出图3中所有天然黏土的χ与Δep的关系（如图4）。如果把结构比变量χ归一化，便可以得到结构性黏土的χ／χ0与Δep关系，如图5所示。由图5可知，随着塑性孔隙比变化量Δep的增加，χ逐渐减小，并最终趋向于0。在一维压缩过程中，χ／χ0和Δep可一一对应。并可用指数函数的形式表达，见式（3）。

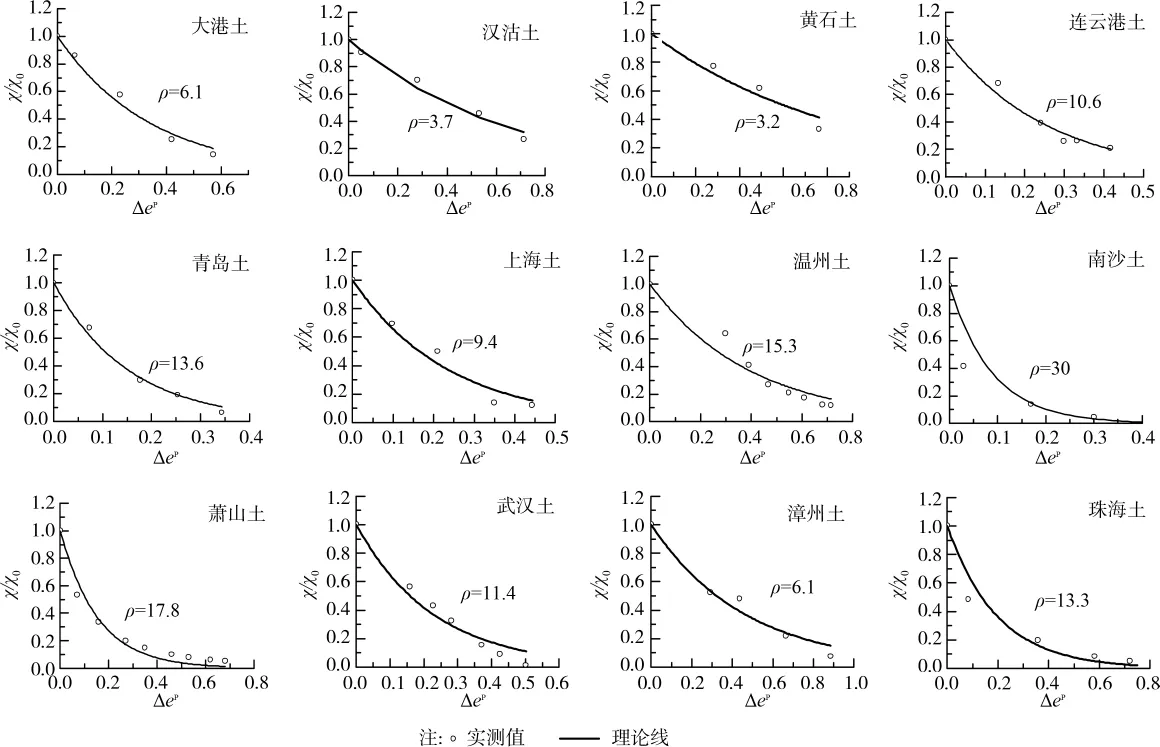
图5 中国12种天然黏土χ／χ0－Δep 关系图

式中ρ为控制土体结构破坏速率的参数。图5列出了各天然黏土的ρ值，变化范围为3.2～30.0。

由图4分析可知，对于重塑土样产生Δep，对应于σv和σp0，σvi和σpi0关系见式（4）。

原状土在塑性阶段时的当前应力σv由式（1）可得式（5）。

把式（3）、（4）代入式（5），可得式（6）。

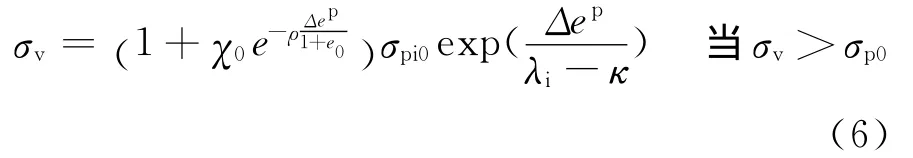
由于模型建立在半对数坐标上，当前应力需要一个初始值，可设为σv0＝10kPa，其相对应的孔隙比为e0′。σv与弹性孔隙比Δee关系可表达为式（7）。

Δee、Δep、e0′和当前孔隙比e之间关系见式（8）。

结合式（6）、（7）、（8），即可计算出结构性黏土的e－σv关系。

2.2 模型参数研究

此压缩模型的参数少，各参数物理意义明确，可以分为以下2类：

1）压缩参数：原状土压缩曲线初始斜率κ，屈服应力σp0，初始孔隙比e0′，重塑土压缩曲线斜率λi，原状土和重塑土e－ln（σ）曲线初始相交点（σpi0，epi0）。

2）结构性参数：初始结构比变量χ0和结构破坏速率参数ρ。其中χ0可直接量取（见图4）。对于ρ的取值，通过式（6）可推导出式（9）。

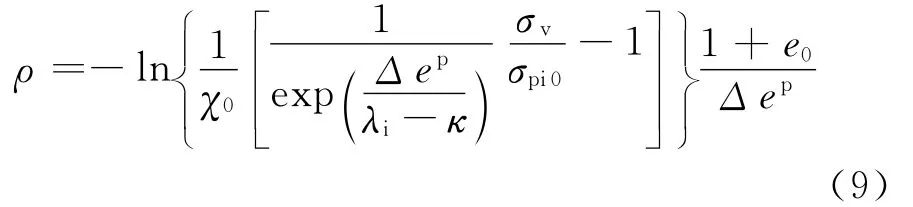
如果在原状土的塑性压缩曲线阶段选取一个点（σv，e），那么式（9）中的 Δep可由式（7）、（8）得到，再代入式（9），便可得到ρ值。

因此，此模型的所有参数只需要量测，并不需要反算便可直接得到。

为了展示模型的一维压缩状态模拟能力，图6给出了由本文模拟计算的汉沽结构性黏土压缩曲线，此土样σpi0＝51kPa，κ＝0.025，λi＝0.302，e0′＝1.32。结构破坏参数ρ从0变化到12，可以看出模型可以模拟不同程度的结构破坏。

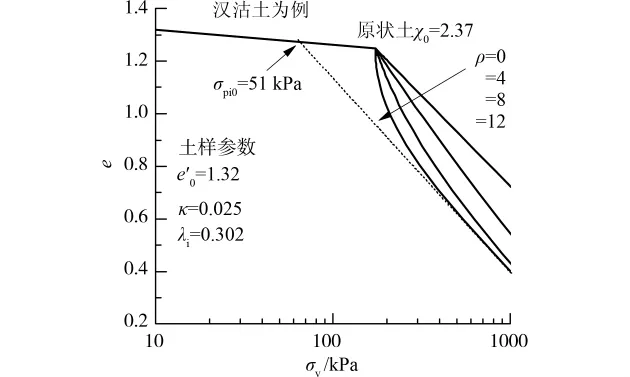
图6 结构破坏速率参数ρ对结构性黏土压缩性状影响

2.3 模型验证

由以上分析可得中国天然黏土的模型参数（见表2），代入式（6）、（7）、（8），联立求得了这些土样的一维压缩计算曲线，并与试验值进行了对比（见图7）。结果完全符合本构公式的建立思想，同时也显示了此模拟方法对于描述中国天然黏土一维压缩特性的适用性。

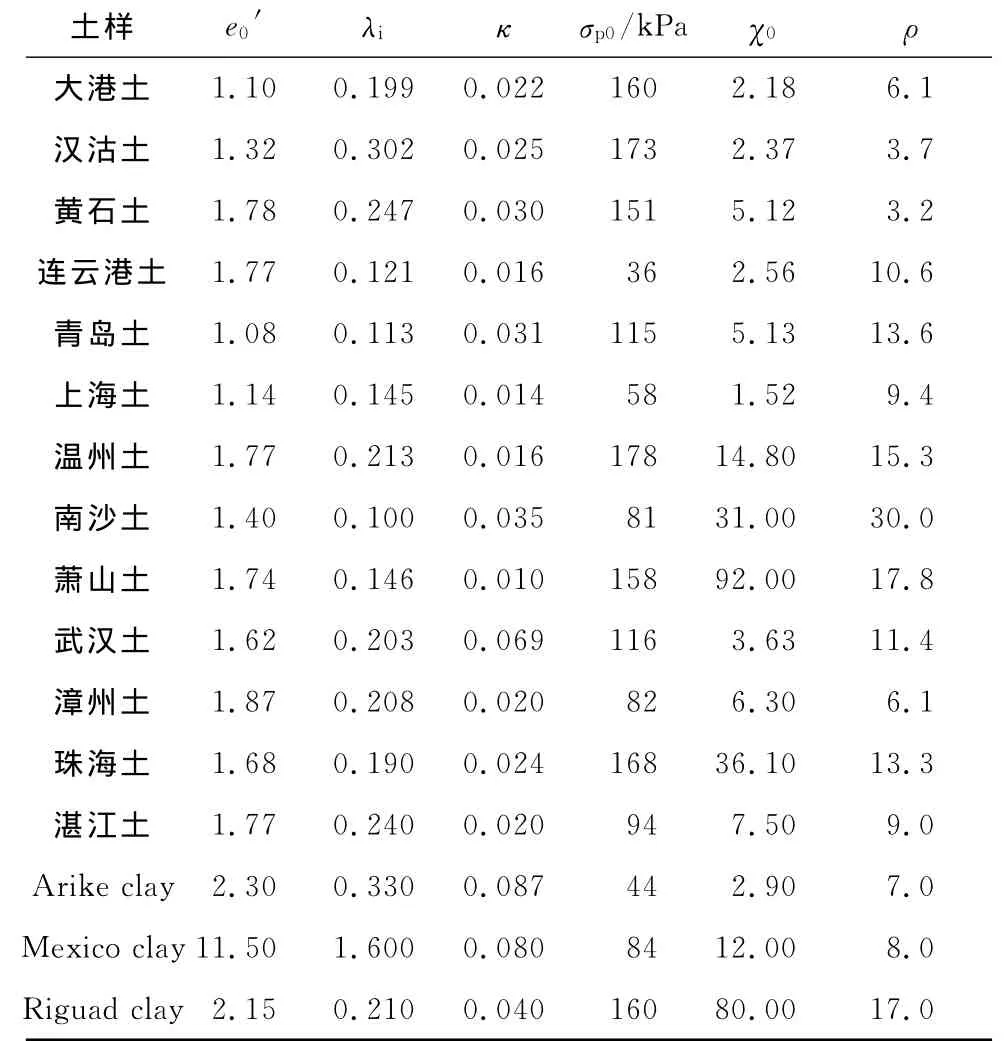
表2 结构性黏土模型参数值

为了进一步验证此一维压缩模型的适应性，应用本模型模拟了其他地区的结构性黏土原状土样的压缩试验，包括中国湛江土［17］（ω＝69%，WP＝21.5%，WL＝59.8%，日本 Ariake clay［12］（D＝6.4 m，ω＝87.4%，WP＝36.8%，WL＝82.2%），墨西哥Mexico clay［13］，和加拿大 Riguad clay［14］（ω＝75%，WP＝25%，WL＝60%）。模型参数确定如前文所述，参数值列于表2。图8为应用本文模型得到的这4种天然黏土的计算曲线与试验结果。这些结果比较显示，所提出的一维压缩模拟方法也适用于不同地区、不同国家的结构性黏土，具有广泛的适用性。上述模拟过程也显示所提出的结构性黏土一维压缩模拟方法简单、便于应用。

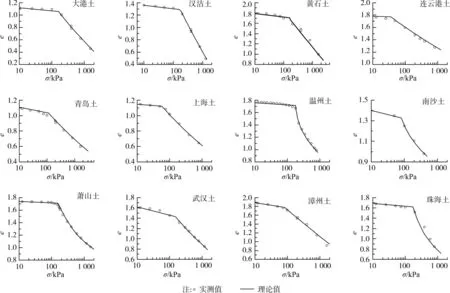
图7 中国12种天然黏土一维压缩试验及模拟结果

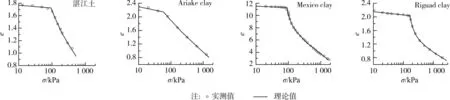
图8 多种天然黏土一维压缩试验及模拟结果

3 扰动状态模型推广

鉴于工程中结构性土极易被扰动，尝试应用扰动状态概念将模型推广为可以描述不同扰动度的土的应力应变关系。

基于扰动状态概念的应变方程［15］一般表达形式见式（10），

式中：εij为应变张量，其中上标i表示材料的实测响应；上标i表示原状土样的响应；上标c表示重塑土样的响应；Dε为扰动函数。

本推广模型通过引入扰动度ds来考虑土体扰动的影响。土体受到扰动后，屈服强度从σp0减小为σp0′，其值见式（11）。

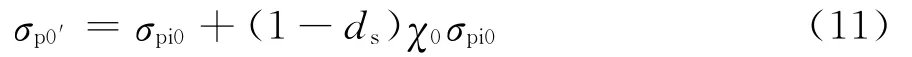
设扰动函数Dε＝dns，式中n为扰动影响参数。式（10）中dεi和dεc可表示为式（12）、（13）。

由于扰动函数为常数，即dDε＝0。把式（12）、（13）代入式（10），可得式（14）。

而当σv＞σp0′时，扰动土压缩曲线通过式（6）、（7）、（8）来计算，此阶段模拟方法与原状土相同。由式（14）可知，对于未扰动土样ds＝0，扰动模型可退化为原状土压缩模型；对于完全扰动土样ds＝1，扰动模型可退化为重塑土模型。

图9为n＝1时，扰动度ds对土体压缩特性的影响曲线；图10为扰动度为40%时，扰动影响系数n对土体压缩特性的影响曲线，土样参考值为汉沽土。由图可见，模型对扰动土体压缩特性的模拟结果与 Hong等［18］、Shogaki等［19］试验结果有相同的趋势。对于给定的试验结果（如：重塑土、原状土、扰动土试验各一个），参数ds和n便可确定。由此，应用扰动状态概念，可以很简单地推广前述结构性土模型来描述不同扰动程度土体的压缩特性。

图9 扰动度ds对土体压缩特性模拟的影响

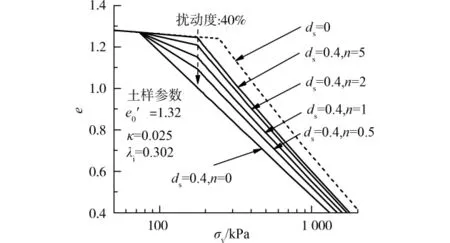
图10 扰动影响参数n对土体压缩特性模拟的影响

4 结 论

调查分析了广泛分布在中国不同地区的12种天然黏土的一维压缩试验。在此基础上，引入“结构比”变量并建立其渐进破坏规律，从而建立了描述结构性黏土一维压缩特性的模拟方法。此一维压缩模型数学表达简单，物理意义明确，参数选取直接，有一定的工程应用价值。

应用此模型验证了中国12种天然黏土的一维压缩试验，并模拟了4种天然黏土。计算曲线与试验曲线的比较显示，所提出的一维压缩模拟方法可以较好地描述结构性黏土一维压缩特性。此模型通过扰动状态概念推广应用，可以很好的模拟扰动状态土的压缩性状，证明此模拟方法也具有广泛的适用性。

［1］Burland J.On the compressibility and shear strength of natural clays［J］.Geotechnique，1990，40（3）：329－378.

［2］Karstunen M，Yin Z Y.Modelling time－dependent behaviour of Murro test embankment［J］.Géotechnique，2010，60（10）：735－749.

［3］王宝勋.海积软土力学特征与固化新技术研究［D］.长沙：中南大学，2008.

［4］张先伟.结构性黏土蠕变特性及扰动状态模型［D］.长春：吉林大学，2010.

［5］邵光辉，刘松玉.海相结构软土的次固结研究［J］.岩土力学，2008，29（8）：2057－2062.SHAO Guanghui，LIU Songyu.Research on secondary consolidation of structural marine clays［J］.Rock and Soil Mechanics，2008，29（8）：2057－2062.

［6］Jiang M J，Peng L H，Zhu H H，et al.Macro－and micro－properties of two natural marine clays in China［J］.China Ocean Engineering，2009，23（2）：329－344.

［7］陈晓平，曾玲玲，吕晶，等.结构性软土力学特性试验研究［J］.岩土力学，2008，29（12）：3223－3228.CHEN Xiaoping，ZENG Lingling，LYU Jing，et al.Expeimental study of mechanical behavior of structured clay［J］.Rock and Soil Mechanics，2008，29（12）：3223－3228.

［8］李玲玲.结构性黏土的性状研究及其应用［D］.杭州：浙江大学，2007.

［9］陈颖平，黄博，陈云敏.循环荷载作用下结构性软粘土的变形和强度特性［J］.岩土工程学报，2005，27（9）：1065－1071.CHEN Yingping， HUANG Bo，CHEN Yunmin.Deformation and strength of structural soft day under cydic loading ［J］.Chinese Journal of Geotechnical Engineering，2005，27（9）：1065－1071.

［10］张勇.武汉软黏土的变形特征与循环荷载动力响应研究［D］.武汉：中国科学院研究生院岩土力学研究所，2008.

［11］Hong Z S，Tsuchida T.On compression characteristics of Ariake clays［J］.Canadian Geotechnical Journal，1999，36（5）.807－814.

［12］洪振舜，刘松玉，于小军.关于结构土屈服破坏的探讨［J］.岩土力学，2004，25（5）：684－687.HONG Zhenshun，LIU Songyu，YU Xiaojun.On destructuration of structured soils［J］.Rock and Soil Mechanics，2004，25（5）：684－687.

［13］Terzaghi K.Fifty years of subsoil exploration［C］／／Proc 3rd Int Conf Soil Mech Found Engng，Zurich 1，Harvard University，1953：227－238.

［14］Silverstri V.Preconsolidation pressure of Champlain clays Part II.Laboratory determination［J］.Canadian Geotechnical Journal，1984.21（3）：600－602.

［15］Liu M D，Carter J P，Desai C S.Modeling compression behavior of structured geomaterials［J］.International Journal of Geomechanics，2003（3）：191－204.

［16］刘维正，石名磊，缪林昌.基于扰动状态概念的结构性土压缩特性分析［J］.岩土力学，2010（11）：3475－3480.LIU Weizheng，SHI Minglei，MIAO Linchang.Analysis of compressibility of structural soils based on disturbed state concept［J］.Rock and Soil Mechanics，2010（11）：3475－3480.

［17］孔令伟，吕海波，汪稔，等.某防波堤下卧层软土的工程特性状态分析［J］.岩土工程学报，2004，26（4）：454－458.KONG Lingwei，LYU Haibo，WANG Ren，et al.Analysis on engineering property of underlying soft soil stratum of a breakwater ［J］.Chinese Journal of Geotechnical Engineering，2004，26（4）：454－458.

［18］Hong Z S，Onitsuka K.A method of correcting yield stress and compression index of Ariake clays for sample disturbance［J］.Soils and Foundations，1998，38（2）：211－222.

［19］Shogaki T，Kaneko M.Effects of sample disturbance on strength and consolidation parameters of soft clay［J］.Soils and Foundations，1994，34（3）：1－10.