含水炭质板岩非线性蠕变损伤模型及应用

张永兴，王更峰，周小平，熊晓晖，王桂林，黄 达

（重庆大学 土木工程学院，重庆400045）

岩石的蠕变特性是工程岩体重要力学特性之一［1］，其往往表现出非线性的流变力学性质，传统的线性元件模型无法反映这点。因此，国内外学者对非线性蠕变模型开展了广泛的研究。Challamel等［2］从连续热力学出发建立了岩石非线性流变软化模型；Vyalov［3］提出了非线性关系的修正Bingham模型；Maranini等［4］基于Cristescu理论提出了岩石蠕变的非关联粘塑性本构方程；Keedwell［5］建立了变弹性模量和变粘滞系数的非线性Kelvin模型；Findley等［6］研究了材料非线性流变性态，得到了不同时刻的蠕变方程。Sun等［7］指出可用非线性元件代替线性元件的方法建立非线性流变模型；陈沅江等［8］提出了蠕变体和裂隙塑性体2种非线性元件；邓荣贵等［9］提出了能描述岩石加速蠕变的非牛顿体粘滞阻尼元件。已取得的研究成果极大的促进了岩石流变力学的发展，但考虑岩体流变含水损伤劣化效应的蠕变模型尚不多见。尤其是遇水强度软化可达0.5～0.8的泥岩、页岩、板岩等软岩［10］。随着含水量的增加，软弱岩体变形的时效积累显著，易引发岩体工程失稳，地下工程岩体长期稳定性依赖于应力与水长期共同作用下的耦合流变过程［11］。因此，研究不同含水条件下软岩的蠕变特性对地下工程围岩长期稳定性有重要意义。

该文结合深埋高地应力隧道大变形段的炭质板岩赋存条件，研究不同含水状态炭质板岩的蠕变特性，通过对不同含水状态蠕变参数的辨识与分析，建立考虑含水损伤且能描述岩石加速蠕变的非线性蠕变损伤本构模型。基于该模型，通过数值计算分析隧道围岩的时效变形规律，为初期支护设计、二衬支护时机及隧道的长期稳定提供理论依据。

1 含水炭质板岩三轴蠕变试验

1.1 试验仪器

蠕变试验在RLW－2000型岩石三轴蠕变试验机上进行，见图1。试验机轴向及侧向应变采用卡环式应变测量装置，最大轴向出力为2 000kN，最大围压为80MPa，仪器稳压效果良好。试验在具有恒温和恒湿条件的蠕变专用实验室内进行，室内温度始终控制在（20±1）℃。

1.2 试验方案

对隧道围岩现场钻芯取样，及时腊封后送至实验室加工成φ50mm×100mm的标准圆柱体试件。采用烘干和泡水试验获得干燥及不同含水状态试样。为模拟炭质板岩的赋存条件，根据现场地应力实测资料，确定蠕变试验的围压恒定为25MPa。具体试验方案见表1，其中每级加载水平按常规三轴压缩得到的岩石抗压强度综合考虑确定。

图1 RLW－2000岩石三轴蠕变试验机

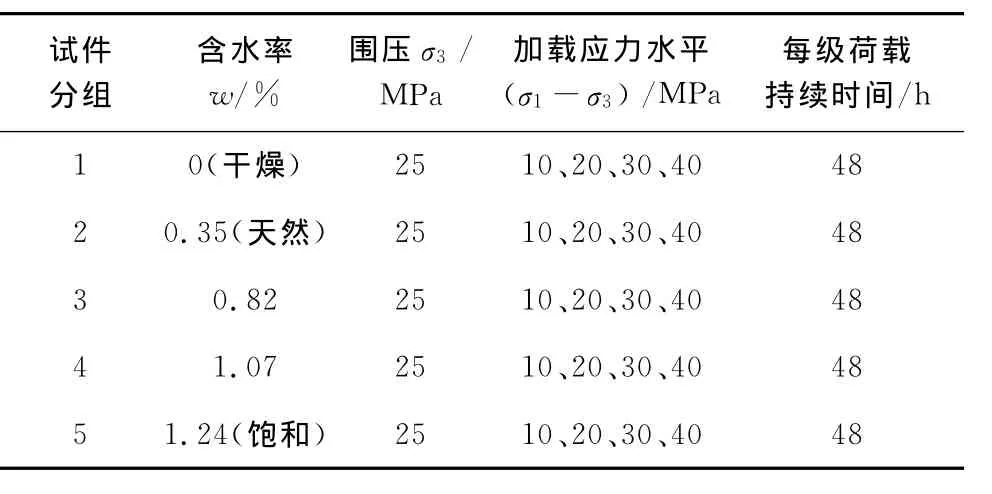
表1 三轴蠕变试验方案

1.3 含水炭质板岩蠕变特性

围压25MPa不同含水状态炭质板岩三轴蠕变曲线如图2所示。可见，当含水率w为1.24%、1.07%及0.82%时随着加载应力水平的提高，出现衰减蠕变、稳定蠕变和加速蠕变3个阶段。而含水率w为0%及0.35%只出现衰减、稳定蠕变。

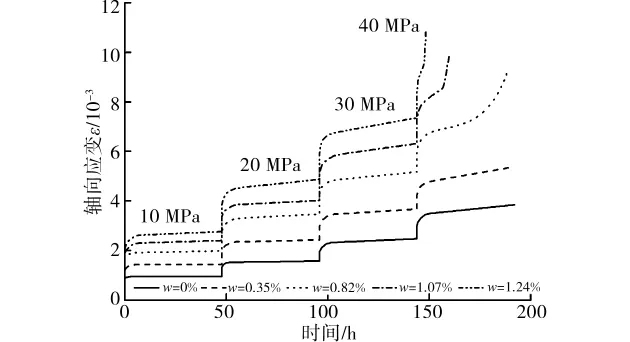
图2 炭质板岩三轴压缩蠕变试验曲线

相同荷载水平随含水率增加，瞬时应变增大，衰减段的曲率半径也增大，进入稳定蠕变所需的时间增加，蠕变应变也越大，且蠕变速率增大［4］；随含水率增加屈服强度σS降低，岩石越快进入加速蠕变阶段，且加速蠕变破坏的时间越短。

表2为不同荷载对应不同含水率炭质板岩蠕变特性指标。分析知，相同含水状态初始瞬间应变随着加载应力水平的增加而增大，稳定蠕变速率也由零逐渐向非零常数变化，蠕变速率逐渐增大。

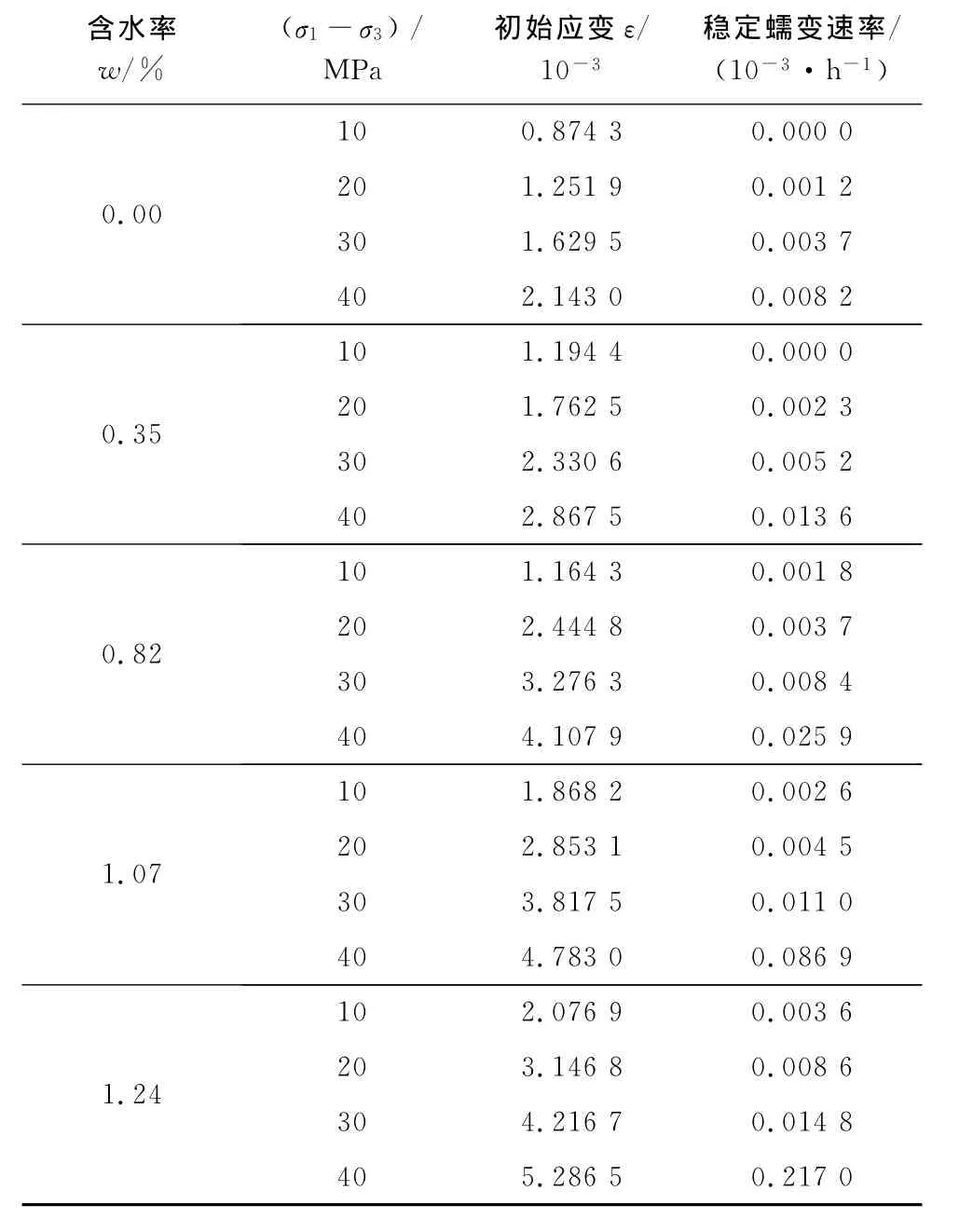
表2 不同含水率蠕变特性指标

2 非线性蠕变本构模型

不同含水状态炭质板岩三轴蠕变试验曲线特征分析表明：1）施加荷载后，岩石立即产生瞬间弹性应变，因此流变模型中应含有H体；2）荷载保持恒定轴向应变有随时间增加而有增大的趋势，可知蠕变模型中还应包含粘性元件［5］；3）当应力水平较高时，应变随时间的增长逐渐增大，应变速率逐渐趋于某恒定值；4）当应力水平达到岩石的屈服强度σS，应变随时间迅速增加，出现加速流变阶段，具有塑性特征。

2.1 非线性粘弹塑性蠕变模型

含水炭质板岩的蠕变呈现出瞬弹性、粘弹性和粘塑性共存复杂特性。适于描述软岩流变模型有Burgers模型、西原模型等，但这些由线性流变元件串并联组合的模型不能反映岩石的加速流变特性［12－13］。本文采用Burgers模型描述岩石瞬时弹性应变、衰减蠕变以及稳态蠕变，然后串联一个可描述岩石加速蠕变特征的非线性粘塑性元件［14－18］，得到一个能反映岩石蠕变3阶段的6元件非线性粘弹塑性蠕变模型，如图3所示。

模型中反映加速蠕变的非线性粘塑性体由非线性粘性元件η（n，t）与塑性体并联而成，其中非线性粘壶本构见式（1）。

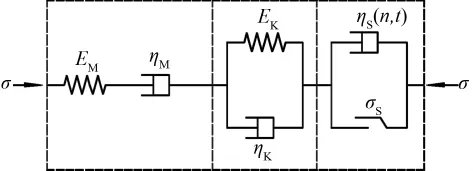
图3 非线性蠕变模型

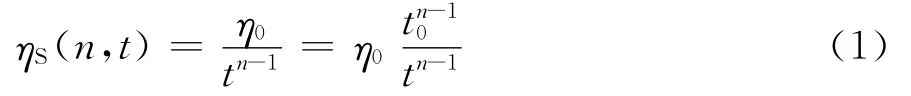
该非线性粘塑性体能充分反映岩石高应力状态下的加速蠕变特征，其相应的蠕变本构方程可表示为式（2），

式中：η0为常量是加速蠕变初期的粘性系数；t0为单位参考时间；σS为岩石的屈服强度；n为加速蠕变参数，反映岩石加速流变速率的快慢程度。式中H的表达式见式（3）。

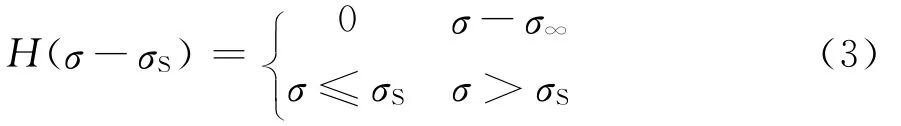
围压下的非线性蠕变模型本构方程见式（4）、（5）。

1）当σ＝σ1－σ3＜σS时，模型退化为Burgers模型，其蠕变本构方程为：

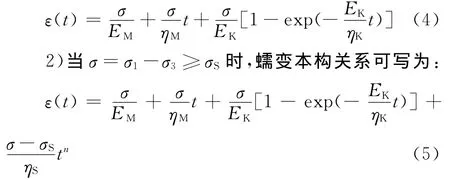
2.2 参数辩识

采用该非线性粘弹塑性蠕变模型，基于1stOPT程序采用L－M算法，对三轴蠕变试验数据进行迭代计算确定模型参数。表3为不同含水率蠕变模型拟合参数。

图4是不同含水状态加速蠕变阶段试验数据及非线性蠕变模型理论曲线，可见拟合效果较好。由表3可知，相同含水状态下岩石各蠕变参数随应力加载水平及持续时间不同呈现非线性变化特征。

3 非线性含水损伤蠕变本构模型

水是造成岩石强度损伤的重要原因，有时它比力学因素造成的损伤更为严重。大量的地下工程实践表明，软岩的流变性是隧道工程围岩变形失稳的重要原因之一。因此，建立考虑含水损伤的非线性蠕变模型对地下工程设计、施工及长期稳定性有着 重要意义。

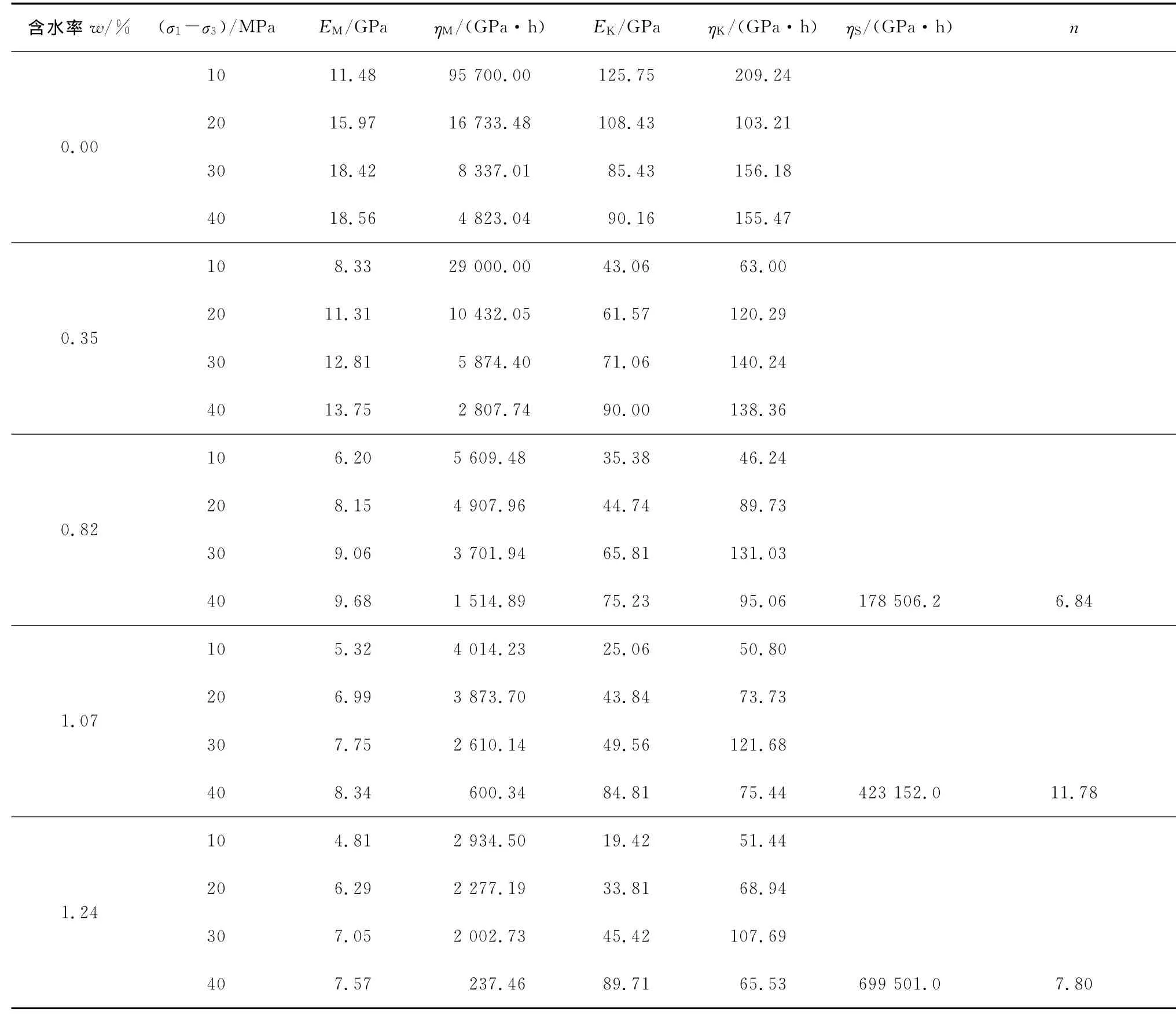
表3 不同含水率非线性蠕变模型参数

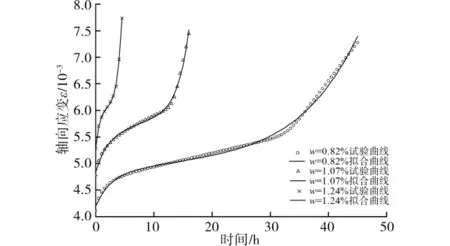
图4 不同含水率加速蠕变试验曲线与拟合曲线

3.1 不同含水率蠕变参数演化规律

主要研究水对炭质板岩蠕变特性的影响，不考虑蠕变参数随应力及时间的损伤劣化。对同一含水率不同荷载下的蠕变参数取平均值，见表4。

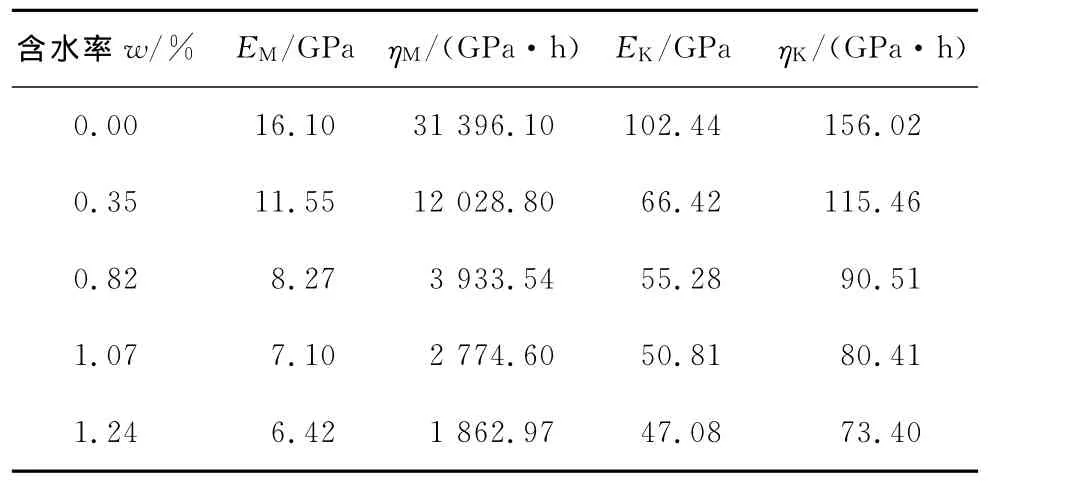
表4 不同含水率蠕变参数平均值

图5～8是根据表4得到的瞬时变形模量EM、粘滞系数ηM、粘弹性变形模量EK、粘弹性粘滞系数ηK随含水率变化的拟合曲线，拟合方程见式（6）～（9）。

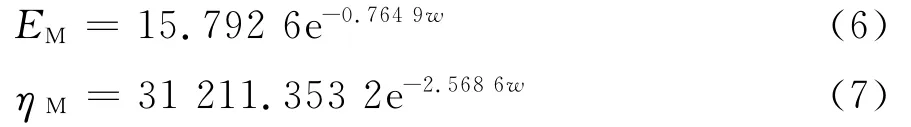
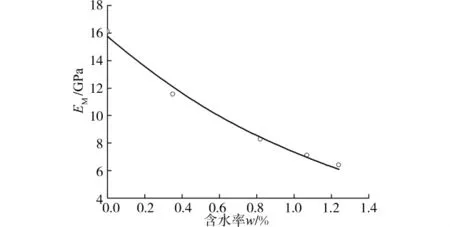
图5 EM随含水率w变化曲线

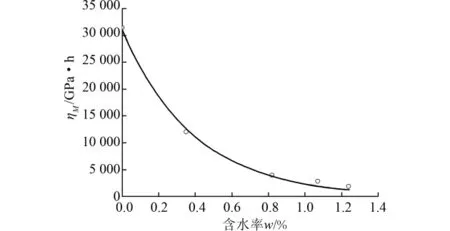
图6 ηM随含水率变w化曲线

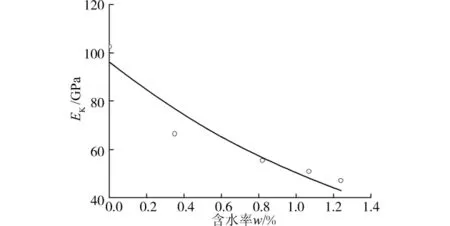
图7 EK随含水率变化曲线

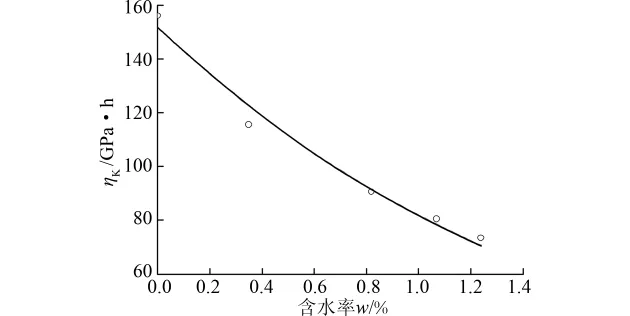
图8 ηK随含水率变化曲线

分析知各蠕变参数随含水率增加呈指数形式y＝ae－bw递减，但各蠕变参数的变化特征并不相同。其中ηM变化最为显著，说明炭质板岩对水的润滑作用比较敏感；随含水率增加瞬时应变增大，EM明显降低；EK、ηK随含水率增加演化特征相似。

3.2 非线性含水损伤蠕变本构模型

蠕变模型中表征瞬间变形的蠕变参数EM的变化是随含水率的增大而减小的，因此含水率变化对EM的损伤可定义式（10），

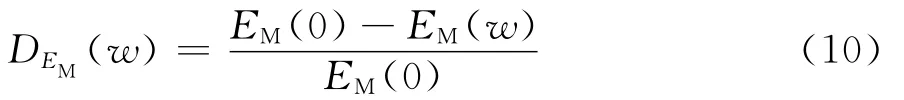
式中：EM（0）为干燥状态时的瞬间变形模量；EM（w）为任意含水状态下的瞬间变形模量。干燥状态损伤为0，随着含水率的增加，损伤变量DEM（w）越来越大，但始终小于1。将不同含水状态炭质板岩对应的平均EM（w）代入式（10）计算出对应的DEM（w），将得到的DEM（w）采用最小二乘法拟合可得EM随含水率w变化的损伤演化方程，见式（11）。

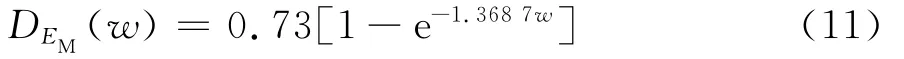
同理可定义ηM、EK和ηK对应的损伤DηM（w）、DEK（w）和DηK（w），计算并拟合得到各蠕变参数的损伤演化方程见式（12）～（14）。

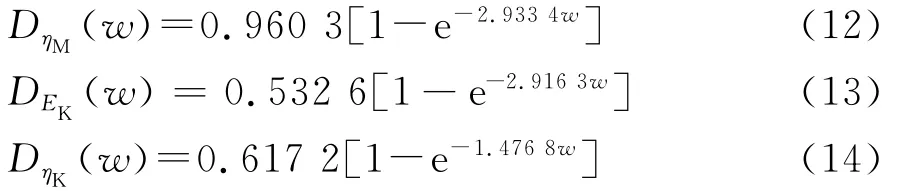
式（11）～（14）对含水率w求偏导可得对应蠕变参数的损伤率演化方程。

参数EM、ηM、ηK、EK的蠕变损伤与含水率w拟合曲线如图9所示，可见随着含水率的增大损伤增大，当含水率为1.24%时，EM损伤达到0.601。ηK、EK的损伤演化规律基本相同。

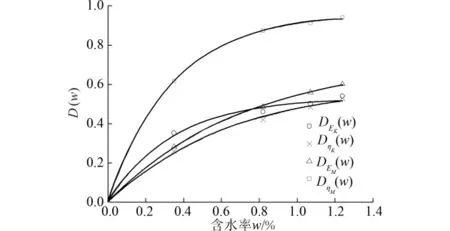
图9 DGM（w）、DηM（w）、DGK（w）及DηK（w）随含水率拟合曲线

将各蠕变参数的含水损伤演化方程代入式（4）、（5）［19－21］建立考虑含水损伤的炭质板岩蠕变本构方程。

1）当σ＜σS时：

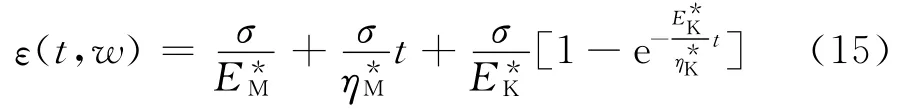
2）当σ≥σS时：

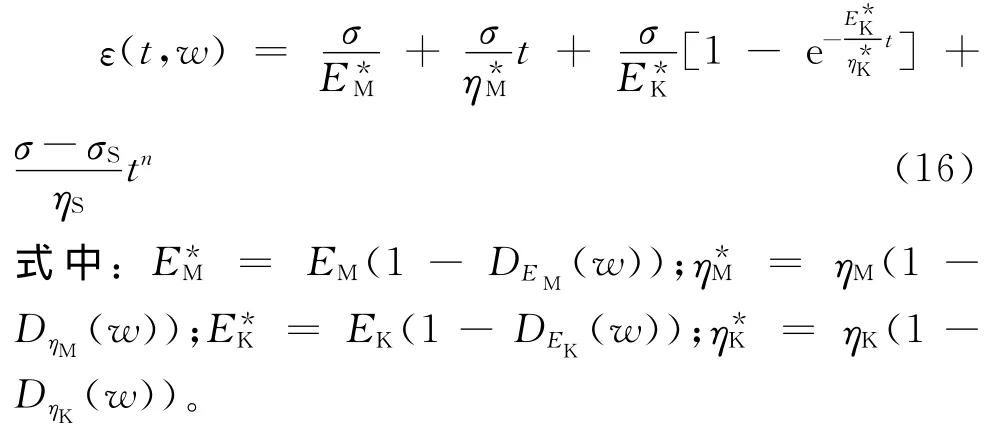
一维状态下的损伤表达式在拓展到三维状态下时，要进行相关假定。采用常体积模量法进行建模，在模型参数转换关系中凡是涉及到泊松比μ时，含水损伤的模型参数损伤表达式也会变化［5］，因此瞬时变形模量GM的含水损伤DGM（w）变化为：

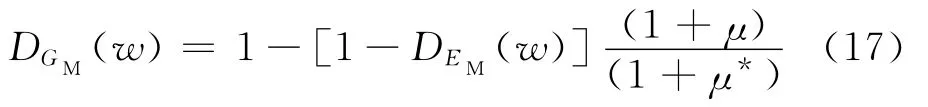
式中：μ为含水率为零时的泊松比；μ＊任意含水率情况下的泊松比。

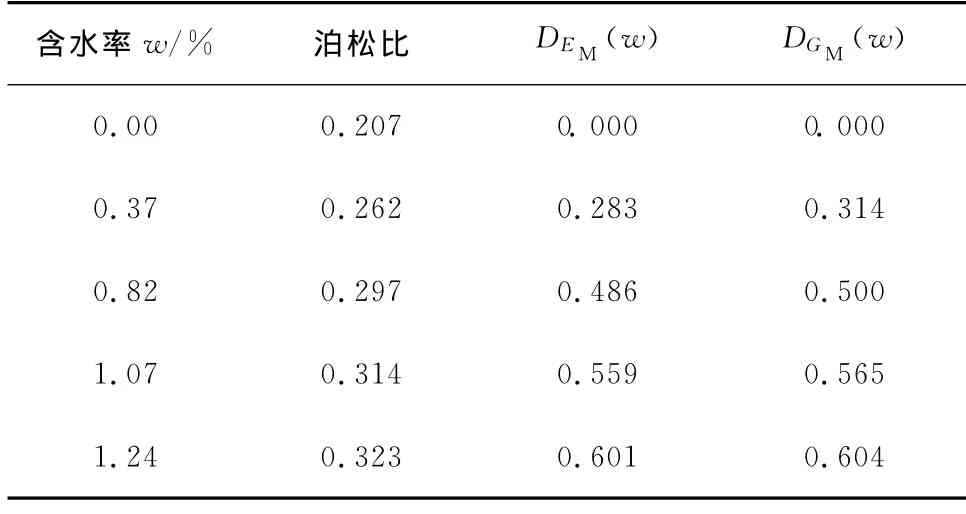
表5 不同含水条件蠕变损伤变量

拟合得到DGM（w）的含水损伤演化方程：

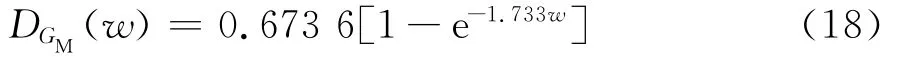
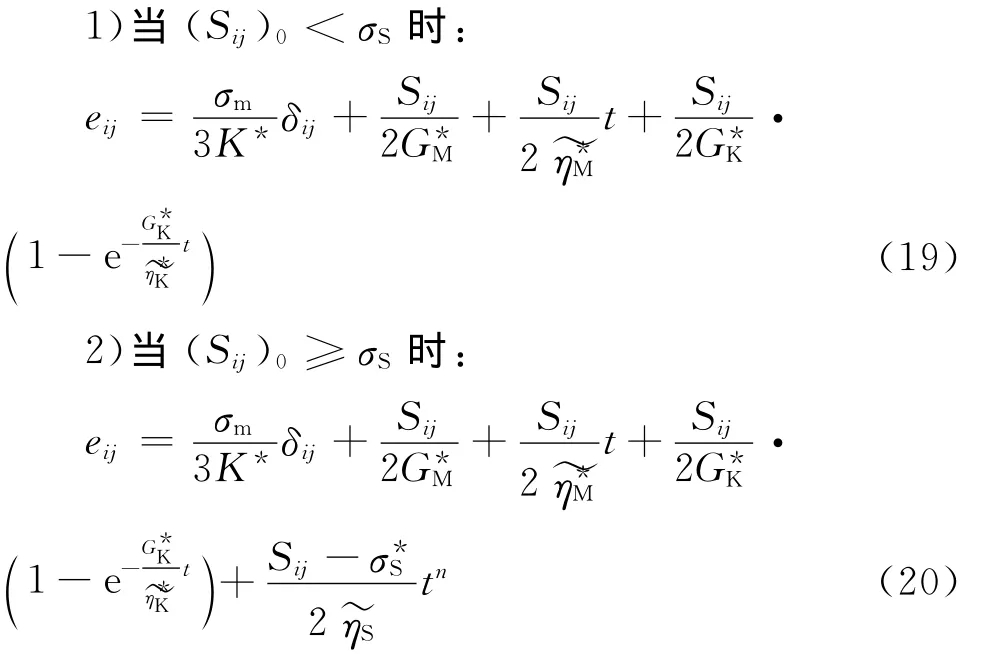
4 含水损伤蠕变本构模型应用

取样隧道长8 503m，最大埋深约700m，区域原岩应力较大且以水平构造应力为主，根据围岩强度应力比判断属于极高地应力状态。隧道采用三台阶弧形导坑预留核心土开挖，设计初支钢架采用I20b，1榀／0.5m。在高应力与地下水双场耦合作用下，隧道开挖后围岩时效变形大，大变形造成初支严重破坏。大变形段地层主要为中、薄层炭质板岩，节理裂隙较发育，裂隙水较大。

初期支护后调整为全环H175型钢，间距0.5m，拱部6m长φ22组合中空锚杆，边墙8m长φ22砂浆锚杆，全环C25喷射砼30cm厚。二衬调整为C35钢筋砼，仰拱厚度为70cm，拱墙厚度为60cm。

地下水对炭质板岩流变特性影响显著，基于所建立的考虑含水损伤非线性粘弹塑性蠕变模型，采用Mohr－Coulomb屈服准则，利用VC＋＋6.0开发环境将本构模型编译成DLL文件，并添加到FLAC3D的动态链接库当中［22－23］。对取样隧道进行自然和饱和状态下的围岩稳定性数值计算［24］，确定合理的初期支护闭合时间与二衬支护时机。

选取隧道埋深450m断面建立数值计算模型，侧压力系数λ＝1.5，分别考虑围岩天然含水状态和饱和状态，围岩基本力学参数见文献［25］，蠕变计算参数按岩体与岩石的粘聚力比值cm／cr＝12.35折减。初期支护采用Shell单元，钢拱架采用等效方法将其强度折算到喷混凝土层。锚杆采用Cable单元，围岩与二衬采用实体单元。分别布置拱顶沉降监测点A及上、中、下台阶水平位移监测点B、C、D，见图14，材料力学参数见表6。

表6 支护材料力学参数

4.1 初期支护封闭成环时间

如图10所示，随含水量增加，开挖后围岩变形量增大，趋于稳定的时间增长，稳定蠕变速率增高。天然含水状态上台阶开挖支护8h后，水平测点B趋于稳定，而拱顶测点A约16h后蠕变变形开始发展。原因在于拱部松动压力大，可适当加长锚杆加固拱部围岩，以及设置锁脚锚杆、临时支撑控制蠕变变形继续发展。

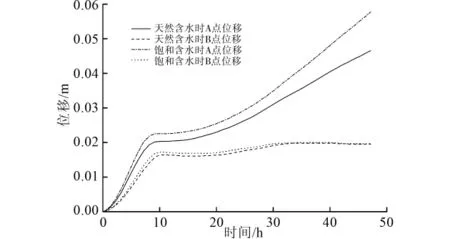
图10 不同含水状态上台阶开挖48h围岩位移

图11 是天然含水状态中台阶开挖120、240、360、480h围岩监测点位移变化情况。文献［25］对兰渝线大变形隧道统计分析的基础上提出高地应力隧道初期支护变形可接受准则：当初期支护累计变形δ≥30cm或单侧变形δ′≥15cm，初期支护钢架扭曲错断、喷射混凝土大面积开裂、掉块，变形不可接受。由图11、12可见，自然含水状态中台开挖约400 h后趋于稳定，饱和含水状态约700h趋于稳定，此时B点位移为0.31m和0.74m，变形必将导致初期支护大面积破坏，不可接受。可见，高应力软岩隧道，应力释放调整时间缓慢，变形持续时间长，在蠕变变形发展至不可接受变形前，初期支护体系宜及早闭合。

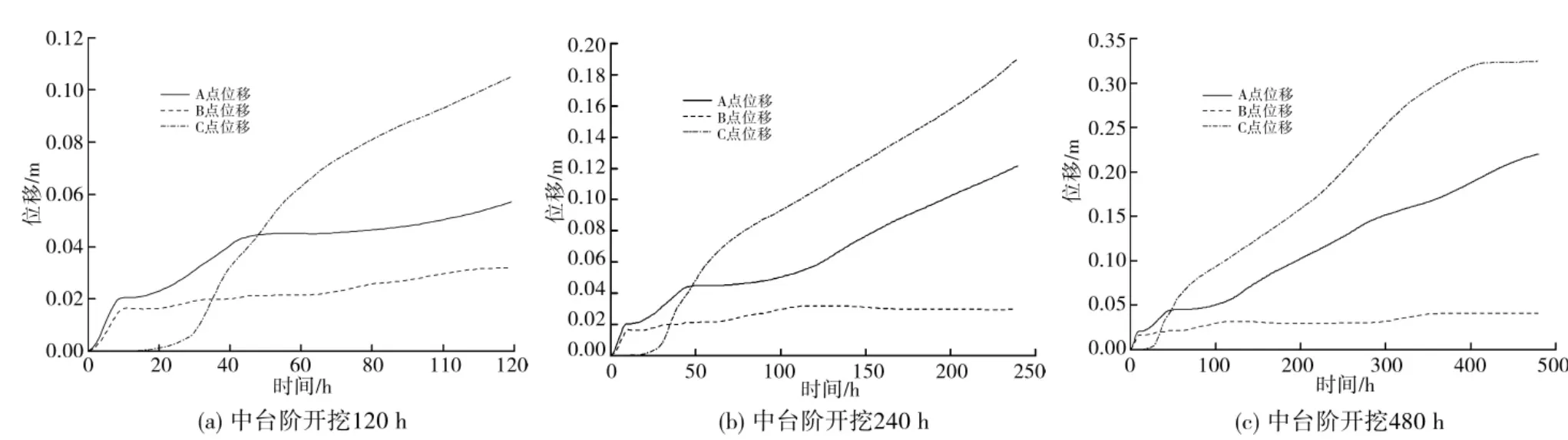
图11 自然含水状态中台阶开挖120、240、480h围岩位移

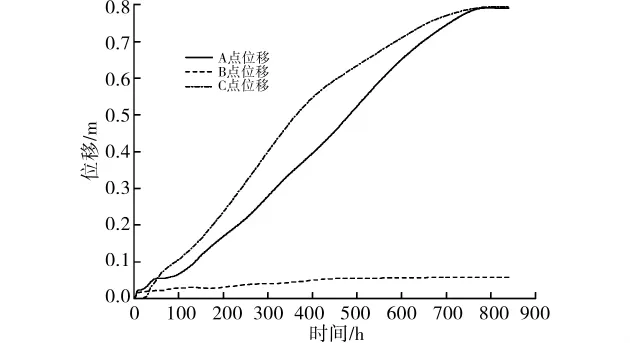
图12 饱和含水状态中台阶开挖围岩位移

合理的确定初期支护封闭成环时间是控制软岩大变形的关键。图13是天然含水状态下台阶开挖初期支护在168h闭合围岩位移变化规律。可见，调整后的初期支护刚度适宜，初支闭合可较好抑制围岩变形的进一步发展，围岩变形速率大大减小，变形趋于稳定。据此，隧道初期支护宜于168h左右闭合，这样既保证围岩有一定的应力释放调整时间，又能控制围岩的蠕变变形继续发展。实际施工过程中，台阶长度应尽可能短，上台阶不宜大于5m，中台阶不宜大于15m，下台阶及仰拱紧跟，保证初期支护尽早封闭。

4.2 二衬最佳支护时机

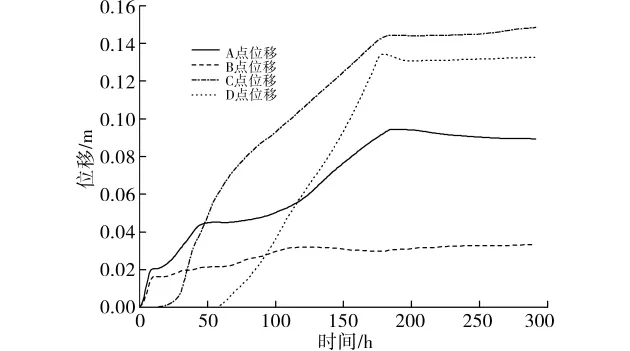
图13 下台阶开及挖初期支护168h闭合围岩位移

大变形软岩隧道二次衬砌浇筑太早，将会导致其承受过大围岩形变压力，使得二次衬砌设计不安全。图14为自然状态初期支护闭合360h后施作二衬围岩位移变化规律，可见，适时施作二衬可承载部分流变压力，与初期支护共同作用抑制围岩蠕变变形，隧道整体处于稳定状态。

4.3 不同含水状态围岩塑性区

隧道开挖168h初期支护闭合前2种含水条件下隧道围岩塑性区分布情况如图15所示。可见，饱和状态开挖168h后的塑性区分布面积较自然含水状态的大。边墙处塑性区面积较拱顶大，这是由于水平构造应力大，导致围岩收敛变形相对较大形成的。在仰拱位置，底鼓变形造成的岩体塑性区面积较大，主要是卸荷引起。若不及时闭合初期支护，围岩塑性区将会进一步发展，导致隧道边墙及底鼓大变形灾害加剧。

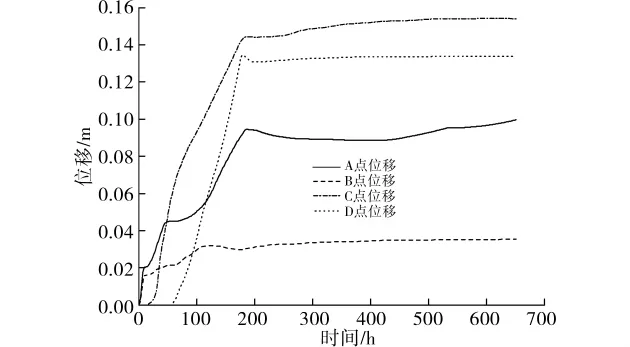
14 自然状态初期支护闭合360h后施作二衬围岩位移

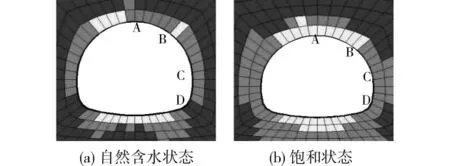
图15 隧道开挖168h后2种含水状态下围岩塑性区

综合上述分析可知，饱和状态下测点围岩变形值较自然含水状态的大。采用当前的支护体系，及早的闭合初期支护，适时施作二衬，能有效控制任意含水状态下围岩变形的发展，隧道整体稳定。

5 结 论

1）通过不同含水条件炭质板岩三轴蠕变试验得到了各蠕变参数EM、ηM、EK、ηK随含水率增加呈指数递减形式，但递减规律并不相同。

2）引入损伤变量D（w），基于试验结果分析得到EM、ηM、EK、ηK随含水率 变 化 的 损伤演化方程DEM（w）、DηM（w）、DEK（w）和DηK（w）。

3）将各蠕变参数对应的损伤演化方程代入非线性粘弹塑性蠕变模型，得到考虑含水损伤效应非线性蠕变本构方程，可描述炭质板岩瞬间弹性变形、衰减蠕变、加速蠕变以及含水损伤特性。

4）研究了不同含水状态隧道围岩的时效稳定性，采用调整后的初期支护与二次衬砌结构，自然状态下初期支护宜在168h左右闭合，能有效抑制围岩蠕变变形继续发展，闭合后360h左右施作二衬，隧道整体处于稳定状态。

［1］孙钧.岩石流变力学及其工程应用研究的若干进展［J］.岩石力学与工程学报，2007，26（6）：1081－1106.SUN Jun.Rock rheolgical mechanics and its advance in engineering applications［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（6）：1081－1106.

［2］Challamel N，Lanos C，Casandjian C.Creep damage modelling for quasi－brittle materials ［J］.European Journal of Mechanics A／Solids，2005，24：593－613.

［3］Vyalov S S.Rheological fundamentals of soil mechanics［M］.London：Elsevier Applied Science Publishingers，1986：231－232.

［4］Maranin E，Brignoli M.Creep behavior of a weak rock：experimental characterization ［J］.International Journal of Rock Mechanics and Mining Sciences，1999，36（1）：127－138.

［5］Keedwell J K.Rheology and soil mechanics ［M］.London：Elsevier Applied Science Publishingers，1984：91－92.

［6］Findley W N，Lai J S，Onaran K.Creep and relaxation of nonlinear viscoelastic materials［M］.North－Holland Publishing Company，1976：196－253.

［7］Sun J，Wang S J.Rock mechanics and rock engineering in China：developments and current state－of－the－art［J］.International Journal of Rock Mechanics and Mining Sciences，2000，37（1）：447－465.

［8］陈沅江，潘长良，曹平，等.软岩流变的一种新力学模型［J］.岩土力学，2003，24（2）：209－214.CHEN Yuanjiang，PAN Changliang，CAO Ping，et al.A new mechanical model for soft rock rheology［J］.Rock and Soil Mechanics，2003，24（2）：209－214.

［9］邓荣贵，周德培，张倬元，等.一种新的岩石流变模型［J］.岩石力学与工程学报，2001，20（6）：780－784 DENG Ronggui，ZHOU Depei，ZHANG Zhuoyuan，et al.A new rheological model for rocks［J］.Chinese Journal of Rock Mechanics and Engineering，2001，20（6）：780－784.

［10］杨文东，张强勇，张建国.不同含水条件下板岩力学实验研究与理论分析［J］.岩土力学，2006，27（9）：1638－1642.YANG Wendong，ZHANG Qiangyong，ZHANG Jianguo.Experimental study and theoretical analysis of slates under different saturated conditions ［J］.Rock and Soil Mechanics，2006，27（9）：1638－1642.

［11］黄小兰，杨春和.不同含水情况下的泥岩蠕变试验及其对油田套损影响研究［J］.岩石力学与工程学报，2007，26（Sup2）：3477－3482.HUANG Xiaolan，YANG Chunhe.Experimental study on mudstones creep behavior under different water content and its effect on casing damage［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（Sup2）：3477－3482.

［12］袁海平，曹平，许万忠.岩石粘弹塑性本构关系及改进的Burgers蠕变模型［J］.岩土工程学报，2006，28（6）：797－799.YUAN Haiping，CAO Ping，XU Wanzhong.Viscoelastop－lastic constitutive relationship of rock and modified Burgers creep model［J］.Chinese Journal of Geotechnical Engineering，2006，28（6）：797－799.

［13］曹树刚，边金，李鹏.岩石蠕变本构关系及改进的西原正夫模型［J］.岩石力学与工程学报，2002，21（5）：632－634.CAO Shugang，BIAN Jin，LI Peng.Rheologic constitutive relationship of rocks and a modifical model［J］.Chinese Journal of Rock Mechanics and Engineering，2002，21（5）：632－634.

［14］徐卫亚，杨圣奇，褚卫江.岩石非线性勃弹塑性流变模型（河海模型）及其应用［J］.岩石力学与工程学报，2006，25（3）：433－447.XU Weiya，YANG Shengqi，CHU Weijiang.Nonlinear viscoelasto－plastic rheological model（Hohai Model）of rock and its engineering application ［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（3）：433－447.

［15］杨圣奇.岩石流变力学特性的研究及其工程应用［D］.南京：河海大学，2006.

［16］徐卫亚，杨圣奇，谢守益.绿片岩三轴流变力学特性的研究（Ⅱ）：模型分析［J］.岩土力学，2005，26（5）：694－697.XU Weiya，YANG Shengqi，XIE Shouyi.Investigation on triaxial rheological mechanical properties of greenschist specimen（Ⅱ）：model analysis ［J］.Rock and Soil Mechanics，2005，26（5）：694－697.

［17］黄明.含水泥质粉砂岩蠕变特性及其在软岩隧道稳定性分析中的应用研究［D］.重庆：重庆大学，2010.

［18］周家文，徐卫亚，杨圣奇.改进的广义Bingham岩石蠕变模型［J］.水利学报，2006，37（7）：827－830.ZHOU Jiawen，XU Weiya，YANG Shengqi.Improved generalized Bingham creep model for rocks［J］.Journal of Hydraulic Engineering，2006，37（7）：827－830.

［19］Li Y S，Xia C C.Time－dependent tests on intact rocks in uniaxial compression ［J］.International Journal of Rock Mechanics and Mining Sciences ＆ Geomechanics Abstracts，2000，37：467－475.

［20］Chna K S，Bodner S R，Fossum A F，et al.A constitutive model for inelastic flow and damage evolution in solids under triaxial compression［J］.Mechanics of Materials，1992（14）：1－14.

［21］Costin L S.Time－dependent damage and creep of brittle rock ［C ］／／Damage Mechanics and Continuum Modeling，ASCE，New York，1985：25－38.

［22］陈卫忠，王者超，伍国军，等.盐岩非线性蠕变损伤本构模型及其工程应用［J］.岩石力学与工程学报，2007，26（3）：467－472.CHEN Weizhong，WANG Zhechao，WU Guojun，et al.Nonlinear creep damage constitutive model of rock salt and its application to engineering［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（3）：467－472.

［23］杨文东，张强勇，张建国.基于FLAC3D的改进Burgers蠕变损伤模型的二次开发研究［J］.岩土力学，2010，31（6）：1957－1963.YANG Wendong，ZHANG Qiangyong，ZHANG Jianguo.Second development of improved Burgers creep damage constitutive model of rock based on FLAC3D ［J］.Rock and Soil Mechanics，2010，31（6）：1957－1963.

［24］Malan D F.Time－dependent behavior of deep level tabular excavations in hard rock［J］.Rock Mechanics and Rock Engineering，1999，32（2）：123－155.

［25］兰渝铁路高地应力软岩隧道施工技术研究［R］.铁道部工程管理中心，2010.