层状粘弹性地基一维固结特性

刘加才，马 强

（南京工业大学 交通学院，南京210009）

地基的固结问题一直是工程界和理论界关心的热点问题之一。Terzaghi最早提出一维固结理论，为固结理论的发展奠定了基础。近年来一维固结理论有了较大发展，可以考虑较为复杂的情况，如加载随时间变化［1］、渗透力对土体固结的影响［2］、土体非饱和［3］、有限应变［4］、土体材料非线性［5］、非达西渗流［6］。软粘土具有粘弹性，地基土层通常具有成层性。一些学者将Terzaghi固结理论推广到成层地基情况，如 Xie等［7］、Lee等［8］。另外一些学者考虑土体的黏滞性，研究了土体的一维固结问题，如赵维炳［9］、Hawlader等［10］、Li等［11］、Xie等［12］。由于问题的复杂性，同时考虑土体的成层性和黏滞性的文献并不多见。Cai等［13］基于Kelvin流变模型，运用Laplace变换、矩阵传递法以及Laplace变换求解了任意荷载下成层粘弹性地基一维变形问题。Kelvin流变模型可以反映弹性后效，却不能反映应力松弛。为了全面反映土体的粘弹性质，刘加才等［14］提出了基于广义Voigt流变模型的双层黏弹性地基求解方法，但求解过程较为复杂，不利于工程应用。本文采用岩土工程中应用较广的Merchant流变模型，提出了层状黏弹性地基的一维固结有限元分析方法，并对其固结特性进行了研究。

1 问题描述

1.1 计算简图

层状粘弹性地基的一维固结问题如图1所示。满足如下基本假定：1）地基土层完全饱和；2）孔隙水和固体颗粒均不可压缩；3）土体渗流满足Darcy定律；4）压缩和渗流仅发生在竖直方向；5）荷载为均布荷载，且瞬时施加；6）地基顶部为排水面，底部为不透水面；7）土体的粘弹性可采用 Merchant流变模型。图中，E0i，E1i，η1i，为第i土层的 Merchant流变模型参数，kvi为第i土层的竖直向渗透系数。深度方向z坐标向下为正，坐标原点为第一层土体顶面。第i土层底面深度为hi。

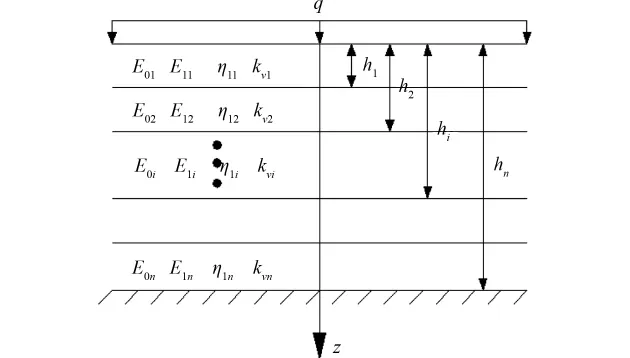
图1 层状黏弹性地基一维固结简图

对于任一土层，满足控制方程式（1）［9，14］。

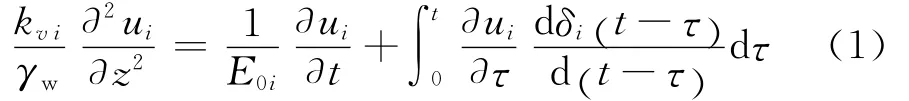
式中：i＝1，2，…，n为土层编号；ui为第i土层的超静孔压；δi为第i土层的Merchant流变模型柔度函数，如式（2）所示。

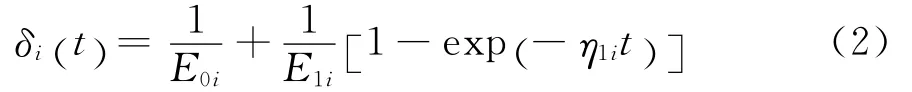
1.2 初始条件

由于荷载为均布荷载，且瞬时施加，任一深度处孔压初始时刻均为q，如式（3）所示。

1.3 边界条件

地基顶面排水，底面不透水，如式（4）、（5）所示：

2 有限元求解及解答有效性验证

2.1 有限元求解

将地基沿固结方向划分为若干2节点单元，节点作为每个单元的边界，土层的分界线作为单元的节点。孔压在单元上线性变化，可用式（6）表示。

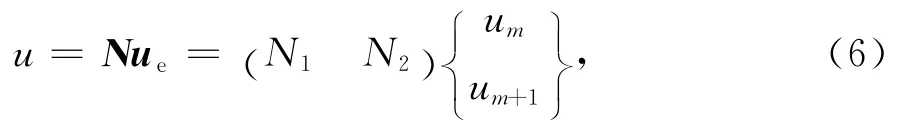
式中：um、um＋1分别代表节点m和节点m＋1处的超静孔压值；N1和N2为形函数，如式（7）所示。

式中：zm、zm＋1分别代表节点m和节点m＋1处的坐标值。

将式（2）和式（6）代入式（1），并利用Galerkin加权残值方法，可得矩阵方程式（8）。

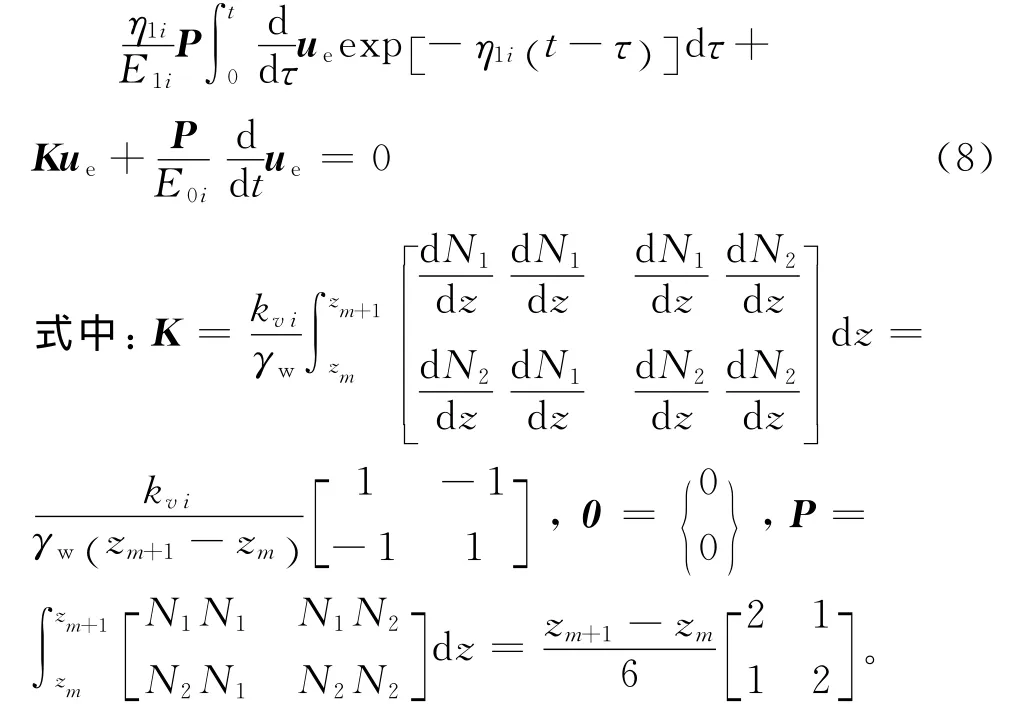
将时间分段，在时间段tj到tj＋1上孔压均为变量，对时间变量进行线性插值，式（8）可整理为式（9）。

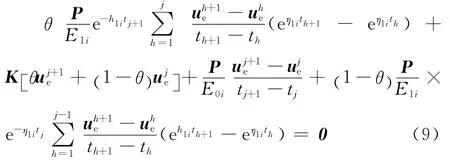
令θ＝1／2，即采用 Crank－Nicolson方法［15］，式（9）可整理为矩阵式（10）。

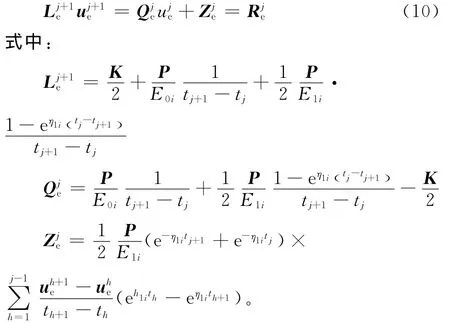
式（10）为每个单元的矩阵方程，采用常规的有限元总矩阵组装方法［15］，形成总的矩阵方程如式（11）所示，从而进一步求解。

在形成总体矩阵后，由于第1个节点为排水节点，超静孔压为0。为方便程序编制，不改变总矩阵的行数和列数，令总矩阵第1行、第1列数加上很大的数，如1015，而方程的右端第一行设置为0。最后1个节点，其外部流量为0，不需做任何特殊处理，在有限元单元矩阵推导过程中已默认为无流量边界。为了便于工程应用，采用Fortran语言将上述有限元求解方法编制成应用程序。

2.2 解答有效性验证

若本文研究的层状黏弹性地基仅有一层，即可简化为单层黏弹性地基一维固结问题。若令Merchant流变模型ηi＝0，即为层状线弹性地基一维固结问题。单层黏弹性地基和双层线弹性地基是本文研究问题的2种特殊情况，其解析解答已分别被赵维炳［9］和Xie等［12］推导获得。为了验证本文求解方法和程序编制的正确性，采用本文程序分别对单层黏弹性地基的固结问题和双层线弹性地基固结进行求解，并与已有精确解析解进行对比分析。

单层黏弹性土层厚度为10m，渗透系数kv＝2×10－9m／s，Merchant流变模型E0＝2MPa，E1＝5MPa，η1＝2×10－8s－1。将土层 划分为 20 个0.5m等长单元，共计21个节点，时间间隔取为1d。图2为100、500、2 000d时，本文有限元方法与解析解在不同深度处土体固结度比较情况。

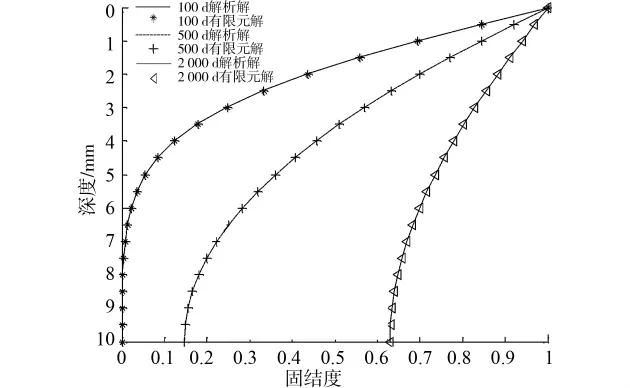
图2 单层黏弹性地基有限元解与解析解比较

双层线弹性土层厚度为10m，第1层土层厚度为3m，渗透系数kv＝1×10－8m／s，压缩模量Es＝5MPa，第2层土层厚度为7m，渗透系数kv＝2×10－9m／s，压缩模量Es＝2MPa。将土层划分为20个0.5m等长单元，共计21个节点，时间间隔取为1d。图3为100d，500d以及1 000d时，本文有限元方法与解析解在不同深度处土体固结度比较情况。

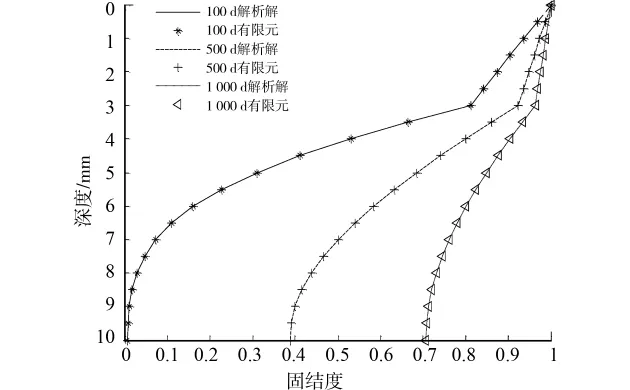
图3 双层线弹性地基有限元解与解析解比较

从以上2个算例的比较情况，可以看出，本文解答与解析解吻合较好，验证了本文求解方法的有效性和程序编制的正确性。

3 层状黏弹性地基固结特性分析

利用本文有限元求解方法，对1个3层黏弹性地基的一维固结问题进行研究，以揭示其固结规律。算例地基土层情况如表1所示：

表1 地基土层参数

图4为考虑黏滞性和不考虑黏滞性时3层地基孔压消散情况。从图中可以看出，不管是黏弹性土体，还是线弹性土体，在土层的分界面处，孔压消散会出现转折点。在时间为100d时，土体的黏滞性对孔压消散的影响并不明显；500d时，第3层土层底部固结度相差10.47%；1 000d时，第3层土层底部固结度相差14.38%。说明，随着时间的增加，孔压消散差别越来越明显，粘滞性土体的孔压消散滞后于线弹性土体。从图中还可以看出，在同一时刻，土体埋深越大，即离排水面距离越远，黏弹性土体固结度越滞后于线弹性土体固结度。

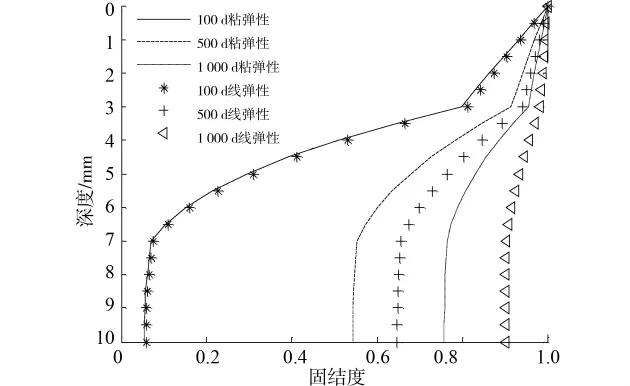
图4 考虑黏滞性与不考虑黏滞性地基孔压消散比较

图5 为土层2和土层3中心点处土体孔压消散随时间变化情况。从图中可以看出，第2层土体黏滞性土体对孔压消散的影响，约在2d左右；而第3层粘弹性对孔压消散的影响约在50d左右。说明随着土层离排水面距离越大，黏滞性对孔压消散的影响也越滞后。不管是第2层土体，还是第3层土体，随着时间的增加，黏滞性土体孔压消散越来越落后于线弹性土体，到某一时刻后两者差距达到最大值，再随着时间的延长，差距又会越来越小。在线弹性土体固结度达到80%～90%时，黏弹性土体与线弹性土体固结固结度差异较大。

图6为第2层土体黏滞性参数η1从1.0×10－7变化到0，该土层土体中心点处孔压消散情况，从图中可以看出，当η1＝1.0×10－9时，与粘弹性土体与线弹性土体固结度差异较小，最大差异值为3%。η1越大，粘弹性土体与线弹性土体固结度差异越大，且对土体的固结度影响也越提前。

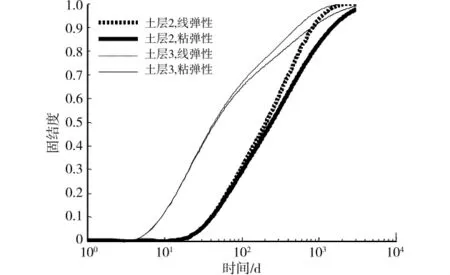
图5 土体孔压消散随时间变化情况

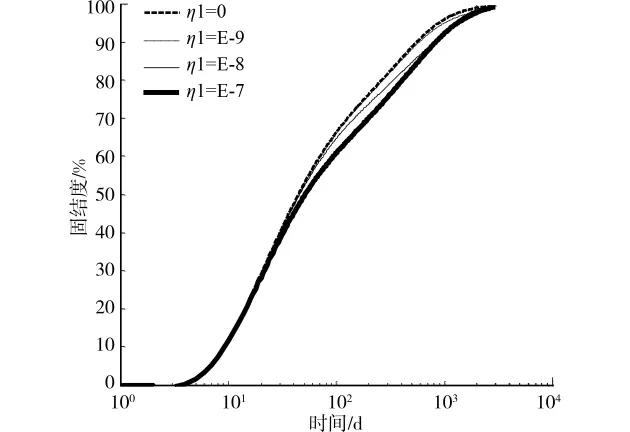
图6 流变参数η1对孔压消散的影响

4 结 语

1）基于 Merchant流变模型，利用Galerkin加权残值方法，推导了层状黏弹性地基一维固结有限元矩阵方程，并给出了求解过程。采用Fortran语言将本文有限元求解方法编制成应用程序。通过单层黏弹性地基和双层线弹性地基一维固结问题本文有限元解答与解析解答的比较，验证了本文求解方法和程序的有效性。

2）对3层地基一维固结研究表明，在土层分界面处孔压消散出现转折点。黏滞性土体孔压消散要滞后于线弹性土体，且随着时间的延长，两者差异会越来越大。同一时刻，随着土体离透水面距离的增大，黏滞性影响会越大。

3）土体的粘弹性对孔压消散的影响时间与其离排水面距离有关，土层离排水面距离越大，黏滞性对孔压消散的影响时间也越滞后。黏滞性土体与线弹性固结度差异呈现两头小中间大的特点。工程中常要求地基固结度达到80%～90%，而这一时间段内考虑考虑土体的粘弹性和不考虑粘弹性固结度差异较大。因此，在实际工程中应考虑土体粘弹性对孔压消散的影响。

4）土体粘弹性参数η1越大，则孔压消散越慢，与线弹性土体固结度差异越大。在实际工程若η1＜1.0×10－9s－1时，粘弹性土体与线弹性土体固结度差异在3%以内，可以不考虑粘弹性对土体固结度的影响。

［1］Hsu T W，Lu S C.Behavior of one－dimensional consolidation under time－dependent loading［J］.Journal of Engineering Mechanics，2006，132（4）：457－462.

［2］Liu J C，Zhao W B，Zai J M.Research on seepage force influence on one－dimensional consolidation ［J］.Geotechnical Special Publication，2006，148：203－209.

［3］Qin A F，Chen G J，Tan Y W，et al.Analytical solution to one－dimensional consolidation in unsaturated soils［J］.Applied Mathematics and Mechanics，2008，29（10）：1329－1340.

［4］Morris P H.Analytical solutions of linear finite－and small－strain one－dimensional consolidation［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2005，29（2）：127－140.

［5］Yang L A，Tan T S.One－dimensional consolidation of lumpy clay with non－linear properties［J］.Geotechnique，2005，55（3）：227－235.

［6］鄂建，陈刚，孙爱荣.考虑低速非Darcy渗流的饱和黏性土一维固结分析［J］.岩土工程学报，2009，31（7）：1115－1119.E Jian，CHEN Gang，SUN Airong.One－dimensional consolidation of saturated cohesive soil considering［J］.Chinese Journal of Geotechnical Engineering，2009，31（7）：1115－1119.

［7］Xie K H，Xie X Y，Jiang W.A study on one－dimensional nonlinear consolidation of double－layered soil ［J］.Computers and Geotechnics，2002，29（2）：151－168.

［8］Lee P K K，Xie K H，Cheung Y K.Study on onedimensional consolidation of layered systems［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1992，16（11）：815－831.

［9］赵维炳.广义Voigt模型模拟的饱水土体一维固结理论及其应用［J］.岩土工程学报，1989，11（5）：78－85.ZHAO Weibin.Theory of one－dimensional consolidation of saturated clays with generalized Voigt model and its applications［J］.Chinese Journal of Geotechnical Engineering，1989，11（5）：78－85.

［10］Hawlader B C，Muhunthan B，Imai G.Viscosity effects on one－dimensional consolidation of clay［J］.International Journal of Geomechanics，2003，3（1／2）：99－110.

［11］Li J Z，Peng F L，Xu L S.One－dimensional viscous behavior of clay and its constitutive modeling［J］.International Journal of Geomechanics，2009，9（2）：43－51.

［12］Xie K H，Xie X Y，Li X B.Analytical theory for onedimensional consolidation of clayey soils exhibiting rheological characteristics under time－dependent loading［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2008，32（14）：1833－1855.

［13］Cai Y Q，Xu C J，Yuan H M.One－dimensional consolidation of layered and viscoelastic solids under arbitrary loading ［J］.Applied Mathematics and Mechanics，2001，22（3）：307－313.

［14］刘加才，赵维炳，宰金珉，等.双层黏弹性地基一维固结分析［J］.岩土力学，2007，28（4）：743－746，752.LIU Jiacai，ZHAO Weibing，ZAI Jinmin，et al.Analysis of one－dimensional consolidation of double－layered viscoelastic ground［J］.Rock and Soil Mechanics，2007，28（4）：743－746，752.

［15］Thomas J W.Numerical partial differential equations：finite difference methods［M］.Beijing：Beijing World Publishing Corporation，1997.

［16］Smith J M，Griffiths D V.Programming the finite element method［M］.4th ed.New York：John Wiley Sons Ltd.，2004.