基于模糊控制的最大功率点跟踪

曹 旭，叶建华，傅培洋

(上海电力学院电力与自动化工程学院，上海 200090)

光伏发电是一种重要的新能源发电方式.在光伏发电系统中将太阳能转换为电能的设备为光伏电池.由于光伏电池的输出电流与电池电压、光照强度、环境温度等参数相关，具有很强的非线性特点.为了使光伏电池在运行过程中的输出电流最大化，就需要控制光伏电池电压以保证光伏电池在较大的光照强度及温度变化范围内实现输出电流的最大化，该控制过程称为最大功率点跟踪(Maximum Power Point Tracking，MPPT)[1-3].

目前，已广泛采用的MPPT方法有梯度跟踪法和电导增量法[2].电导增量法是通过调整工作点的电压，使之逐渐接近最大功率点电压来实现最大功率点的跟踪，该方法避免了梯度跟踪法的盲目性，它能够判断出工作点电压与最大功率点电压之间的关系[3].其缺点在于调整步长的选择较为困难，若采用较小步长，则控制精度较高而跟踪速度下降;若采用较大步长则能够获得较好的跟踪速度，但牺牲了控制精度.本文研究了一种光伏发电系统的控制结构，设计了基于模糊控制的最大功率点跟踪控制器.

1 光伏电池的仿真模型

光伏电池的物理特性较复杂，在仿真过程中为了突出最大功率点偏移的特点，可采用如图1所示的简化结构进行分析[4].图1中，受控电流源IPV与光照强度K近似成正比，输出电流IDC是IPV与半导体漏电流ID之差.

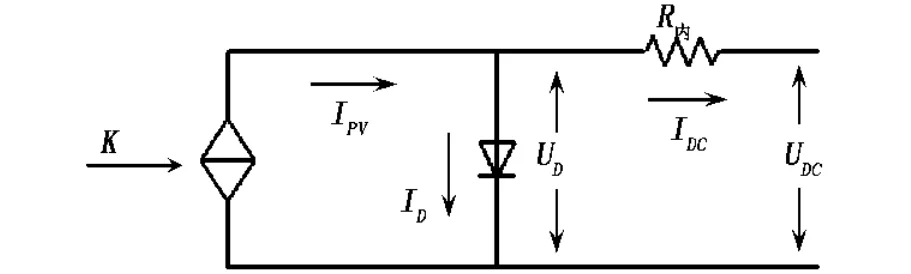
图1 光伏电池仿真模型

若半导体端电压UD小于其正向导通电压，则ID很小，输出电流IDC近似等于光生电流IPV.在光照强度K不变的前提下，端口电压UDC越高，光伏电池的输出功率越大;若UDC提高到一定程度直至半导体端电压UD大于其正向导通电压，则半导体漏电流ID迅速增加，输出电流IDC迅速减小，导致光伏电池的输出功率减小.因此，在确定的工作范围内，光伏电池的功率/电压特性曲线存在一个极值点.

该模型特性的仿真曲线如图2所示.

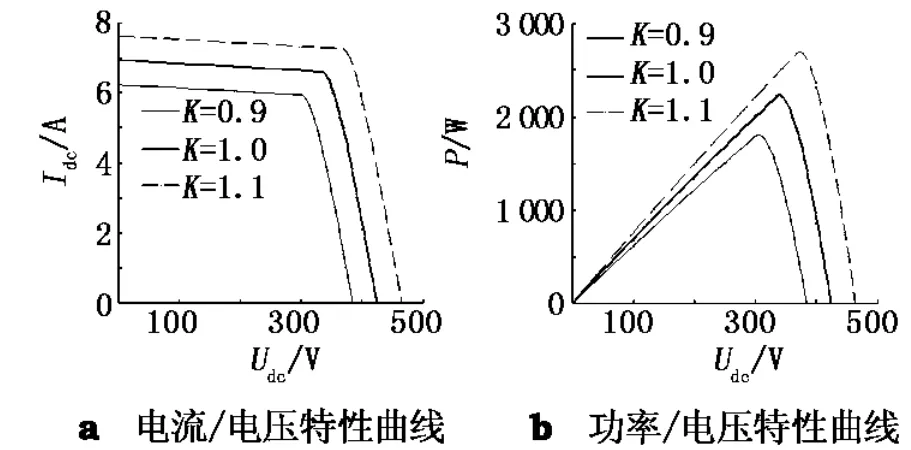
图2 光伏电池特性曲线

由图2可见，当光照强度K由0.9(p.u.)变化至1.1(p.u.)时，光伏电池的最大输出功率不断上升;在光照强度不变的条件下，光伏电池的输出功率先随着电压的上升而上升，至最大输出功率点后随着电压的上升而下降.对应光照强度的最大功率点参数见表1.

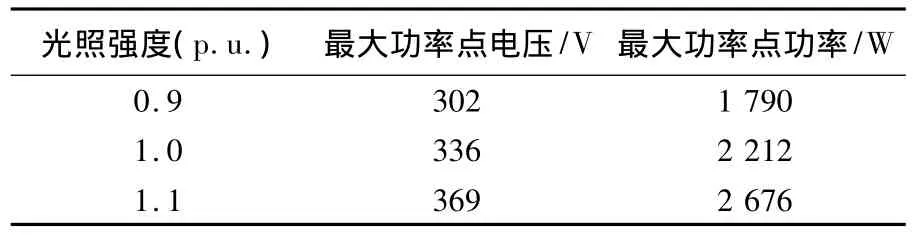
表1 光伏电池最大功率点参数

2 光伏发电系统的控制结构

光伏发电系统的结构如图3所示[3-5].在本文的仿真中选取单相逆变器作为并网接口，但所采用的光伏发电系统控制结构同样适用于三相逆变器接口的光伏系统.

图3 光伏发电系统结构示意

由图3可以看出，该发电系统的能量入口为光伏电池，能量出口为电网，控制系统的总体设计目的就是为了最大限度将太阳能转化为交流电能.根据光伏电池的最大功率点特性设计出的光伏发电系统控制策略见图4.

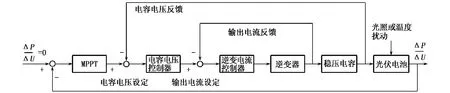
图4 光伏发电系统控制示意

该控制系统共包含1个执行机构——逆变器，以及3个控制回路——MPPT回路、电容电压控制回路和逆变电流控制回路.其中，电容电压控制回路和逆变电流控制回路可采用PID控制器实现，而MPPT回路则需要采用模糊控制实现.将MPPT的跟踪结果作为电容电压控制回路的设定值，并将电容电压控制回路的控制结果作为输出电流的设定值.由于一般光伏系统不承担电网的无功及电压调节任务，因此输出电流的相位设定与实际交流电网电压相位保持一致即可，最终通过逆变器调制输出电流，将光伏电池所产生的能量送入电网.

图4中，MPPT的控制目标为:

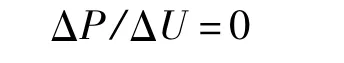
式中:ΔU——光伏电池端电压UDC在每一个控制周期内的改变量;

ΔP——光伏电池输出功率对应ΔU在每一个控制周期内的改变量.

令二者比值为零的目的是为了追踪光伏电池功率特性曲线的峰值点.

3 模糊MPPT的设计

模糊逻辑控制(Fuzzy Logic Control)简称模糊控制(Fuzzy Control)，是以模糊集合理论、模糊语言及模糊逻辑推理为基础的控制，它是模糊数学在控制系统中的应用，是一种非线性智能控制[6-8].

模糊控制是利用人的知识对控制对象进行控制的一种方法，通常用“if条件，then结果”的形式来表现，所以又通俗地称为语言控制.一般用于无法以严密的数学表示的控制对象模型，即可利用人类的经验和知识来很好地控制.而光伏电池正是一个强非线性系统，其不同光照强度下的最大功率点难以用精确的数学模型描述出来，因此采用模糊控制的方法来进行光伏电池的最大功率点跟踪是非常合适的.

模糊控制器的设计主要包括以下3项内容[8，9]，即:确定模糊控制器的输入变量和输出变量;归纳和总结模糊规则表;确定隶属度函数.

3.1 输入和输出变量的确立

在已对光伏发电系统的控制结构进行阐述的基础上，可以确定模糊MPPT为双输入单输出控制器，其输入变量为直流电压UDC与直流功率P各自的差分，输出为电容电压设定值Uset.

由于在不同光照条件下最大功率跟踪点的电压值不同，为便于设计其推理规则及隶属度函数，Uset宜采用离散增量加积分的形式.隶属度函数设计见图5.

图5 隶属度函数设计

3.2 推理规则的确立

对光伏电池输出功率P与电压UDC之间的特性曲线进行分析，并且考虑到日照强度对光伏电池输出功率的影响，得到以下3个原则[5-7]:

(1)不论直流电压变化方向是增加还是减小，若直流功率变化方向为正，则继续原来的电压调节方向，否则取相反的电压调节方向;

(2)若较小的电压偏移能获得较大的功率增加，说明此时光伏电池工作于最大功率点较远处，宜采用较大步长以加快跟踪速度，若较大的电压偏移只能获得较小的功率增加，说明光伏电池工作于最大功率点附近，宜采用较小步长进行搜索以减小搜索损失;

(3)若较小的电压偏移能使直流功率变化反向，则应采用极小步长进行搜索.

遵循上述原则，并针对实际仿真结果进行调整得到最终控制规则表如表2所示.

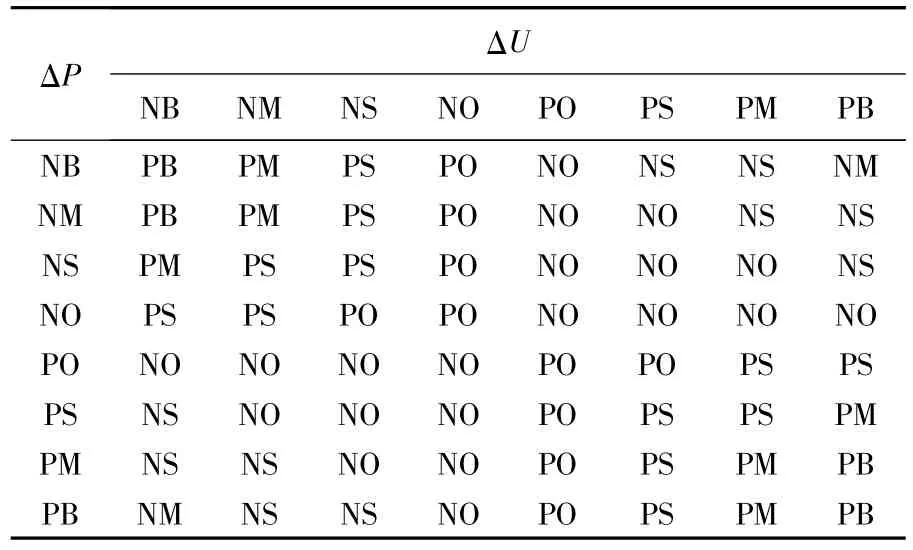
表2 MPPT模糊规则(ΔUset)

3.3 确定隶属函数

在确定模糊规则表后，可设定各输入输出变量的隶属度函数.通过多次仿真实验，确定图6所示的隶属度函数具有较好的控制效果.

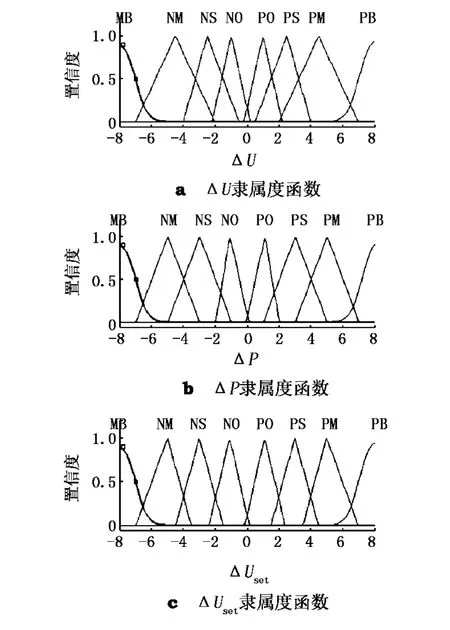
图6 各隶属度函数设计

4 模糊MPPT的仿真结果

依据前述的光伏发电系统及其控制方案进行的仿真结果如图7所示.其中，图7a为光照系数曲线，为了突出最大功率点跟踪的效果，在仿真中假设光照强度是以阶跃信号的形式变化.图7b和图7c分别为对应光照系数的最大功率点直流电压曲线与直流功率曲线.

由图7a，7b，7c 可知，对应 0.9(p.u.)的光照系数，通过模糊MPPT跟踪控制得到的最大功率点电压约为300 V，直流功率约为1 700 W;对应1.0(p.u.)的光照系数，模糊MPPT跟踪控制得到最大功率点电压约为330 V，直流功率约为2 200 W;对应1.1(p.u.)的光照系数，模糊MPPT跟踪控制得到最大功率点电压约为370 V，直流功率约为2 600 W.无论是光照增强或是减弱过程，对应相同的光照系数，跟踪所得最大功率点电压与直流功率均相同，并且该跟踪结果与前述的光伏电池的理论分析结果(表1)一致.仿真结果表明，模糊MPPT具有良好的控制精度，且在光照突变过程中MPPT的跟踪速度保持在5 s左右，具有较好的跟踪速度.图7d所示交流有功功率曲线与直流功率曲线在变化趋势上保持一致，但由于光伏发电系统的直流母线电压始终处于波动状态，导致逆变器输出波形含有较高的谐波，使交流有功出现频繁的波动.因此，在光伏发电系统中需采用适当容量的储能装置以平衡MPPT所带来的直流电压波动，为逆变器提供更稳定的直流电压以减少逆变过程所造成的交流谐波.

图7 模糊MPPT仿真结果

5 结语

本文依据光伏电池的输出功率特性，建立了光伏电池的仿真模型;研究了一种光伏发电系统的控制结构并分析其工作原理;设计了基于模糊控制的最大功率点跟踪控制器，将其应用于光伏发电系统并进行了仿真验证.仿真结果表明该方法能够精确地进行最大功率点跟踪并且具有较快的跟踪速度，光伏电池直流端电压的频繁波动会导致逆变器输出波形含有较高的谐波.因此，为使光伏发电系统能够获得更加稳定的直流电压，减少谐波输出，还需要进一步研究包括储能装置在内的光伏发电系统的控制策略.

[1]陈敏，陈尚伍，钱照明.太阳电池最大功率点追踪的控制策略[J].太阳能学报，2007，28(12):1 317-1 320.

[2]余世杰，何慧若，光伏水泵系统中CVT及TMPPT控制比较[J].太阳能学报，1998，12(4):394-398.

[3]SHIBINI M A，RAKHA H H.Maximum power point tracking technique[C]//Integrating Research，Industry and Education in Energy and Communication Engineering，Lisbon，Portugal，1989:21-24.

[4]KOUTROULIS E，KALA K，VOULGARIS C.Development of a microcontroller-based photovoltaic maximum power point tracking control system [J].IEEE Trans.on Power Electronics，2001，16(1):46-54.

[5]任碧莹，钟彦儒，孙向东，等.基于模糊控制的最大功率点跟踪方法研究[J].电力电子技术，2008，42(11):47-48.

[6]张玉平，石新春，陈雷.光伏系统最大功率跟踪控制的仿真研究[J].灯与照明，2008，32(4):51-55.

[7]王传辉，罗耀华.太阳能电池最大功率点的模糊控制方法[J].应用科技，2008，35(3):42-45.

[8]刘朝英，宋哲英，宋雪.MATLAB在模糊控制系统仿真中的应用[J].计算机仿真，2001，18(3):11-13.

[9]鄢婉娟.一种实现太阳阵峰值功率跟踪的智能控制方法[J].中国空间科学技术，1997，51(2):52-58.