环路声学共振多级行波热声发动机的机理研究
张 爽 罗二仓
(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190)(2中国科学院研究生院 北京 100049)
1 引言
热声发动机是一种将热能转换为声功的新型热机,因其无运动部件、使用寿命长、运行安全可靠、对环境友好而受到人们的广泛关注。热声能量的转换在很大程度上决定于压力波动与体积流率波动之间的相位差。体积流率可表示成与压力波动同相的行波分量和与压力波动相位相差π/2的驻波分量之和,只有行波分量才能产生声功[1]。因此,使声场中行波分量尽量增大对提高热声机械转换效率具有积极的意义。行波热声发动机的概念最早由美国的Ceperley于1973年提出,但他对降低行波热声发动机产生热功转换核心部件-回热器阻抗没有提出有效降低的技术方案,因此并没有研制出可工作的行波热声发动机[1]。1998年,在行波热声发动机发展之初,日本的Yazaki、Iwata等人提出了环形管行波热声发动机[2],他们在研究中意识到由于发动机板叠处声阻抗低,工作气体振动速度较大,造成了严重的粘性损失,限制了行波热声发动机的效率,但是并没有提出妥善的解决方案。随后,美国的Backhaus和Swift等人提出的热声斯特林热机[3]及一些类似结构的热声发动机[4],虽然在系统性能上有了很大的提高,但是谐振管部分基本仍是以驻波声场为主,谐振管中贮存了一定的能量无法得到充分的回收和利用。2010年,荷兰的Kees de Blok提出了一种新型4阶行波热声发电机[5],其结构与Yazaki等人环形管行波热声发动机类似,但是增大了回热器的面积,使得工作气体振荡速度在回热器里有效降低,解决了Yazaki等人环形管行波热声发动机回热器中粘性损失的问题。
本文针对一种闭合环路声学共振多级行波热声发动机的工作机理进行了分析。该发动机的声场中行波分量较大,沿程压力波动与体积流率波动相位差较小。同时,通过增大回热器横截面积,可有效降低了回热器内部气体振荡速度,有效降低了回热器内的粘性损失,使得这一发动机具有潜在高效率。理论上可以将任意多个基本单元串接在一个环路中,在较为紧凑的结构下获得更多的声功,具有发展潜力和应用前景。本文通过数值模拟计算,重点对环路声学共振4级行波热声发动机性能参数的沿程分布进行了考察,并比较了4级、8级、16级行波热声发动机的工作性能。
2 环路声学共振多级行波热声发动机原理
环路声学共振多级行波热声发动机的结构如图1所示,它是由4个结构完全相同的基本单元构成,每个基本单元包括回热器单元和谐振管单元两大部分。回热器单元包括主水冷器、回热器、加热器,谐振管单元包括热缓冲管、次水冷器以及谐振管。回热器单元采用方形结构并具有较大的横截面积,而谐振管单元横截面为圆形,且面积相对较小。主要结构尺寸如表1所示。
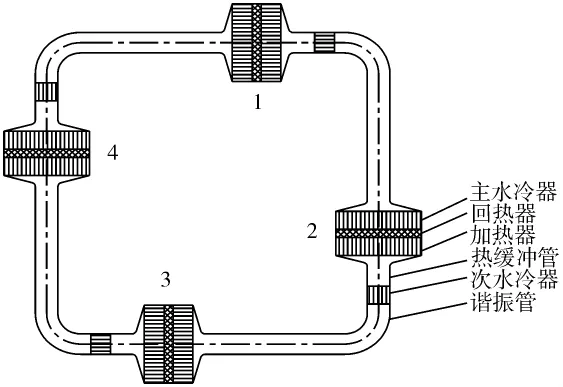
图1 环路声学共振多级行波热声发动机结构示意图Fig.1 Schematic diagram of a looped multi-stage traveling wave thermoacoustic engine

表1 环路声学共振多级行波热声发动机主要结构参数Table 1 Dimensions of looped multi-stage traveling wave thermoacoustic engine
回热器中的粘性损失对于行波系统来说是非常重要的。增大回热器的横截面积,对于体积流率波动影响较小,但可以有效降低回热器中气体振荡速度,从而降低了回热器中的粘性损失。尽管突变截面会导致一些能量损失,但是通过对连接处流动结构的优化设计,能够预期这些损失的影响将有效降低。
在环路结构中,谐振管中的能流能够传递给下一个基本单元,得到回收,因此应该可以获得更高的效率。同时,环形结构有利于加入多个基本单元,在保持整个环路中所有的谐振管单元总长度一定的情况下,系统的一些性能参数变化不大,但是更多的回热器单元能够产生更多的声功,从比例上来说,单个发动机结构也变得相当紧凑。
3 环路声学共振多级行波热声发动机性能分析
3.1 计算模型
通过数值模拟计算分析了环路声学共振多级行波热声发动机的工作性能,模拟中采用了DeltaEC6.2软件[6]。对于气体工质,其控制方程如下[7]:
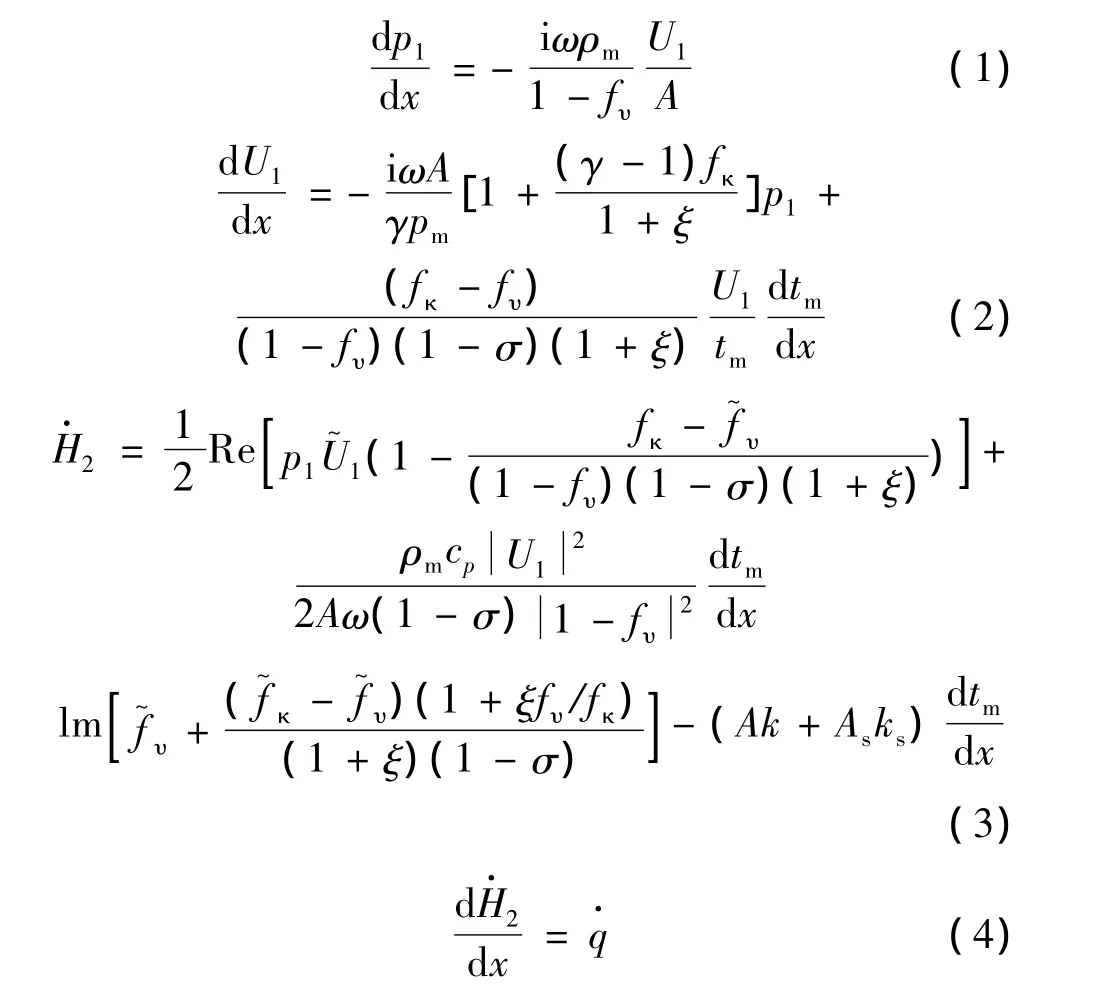
式中:p1和U1为一阶压力波动幅值和体积流率;i为虚数符号;ω为角频率;A为流道截面积;ρm,pm,tm分别表示气体的平均密度、压力和温度;γ,cp,k,σ为气体的比热比、比定压热容、热导率和普朗特数;复变量fυ和fκ与流道的几何参数和工质的物性参数有关,As和ks表示流道固体的截面积和热导率;ξ为壁面热物性参数的修正系数;Re和Im分别表示取实部和虚部;~表示取复数的共轭;‖为复数的幅值;为总功为单位长度的加热量。
3.2 环路声学共振4级行波热声发动机性能分析
本节主要对环路声学共振4级行波热声发动机的无负载性能进行分析。由于系统的对称结构,因此只对其中一个基本单元进行讨论。在整个闭合环路中,体积流率和压力波动的相位均分别变化了360°,因此,对于环路声学共振4级行波热声发动机中的一个基本单元来说,其进口和出口处的体积流率和压力波动的相位分别变化了90°。计算中平均工作压力pm为2.5 MPa,主水冷器与次水冷器壁温tc1、tc2均为室温20℃,加热器壁温th固定为180℃。加热器壁温不是很高,有利于采用低品位能源驱动。
图2—图6给出了压力波动幅值p1、压比pr、体积流率U1、气体振荡速度V、相位角ph、声功率E以及总能流H沿装置长度x的沿程分布(位置说明:0—0.022 m主水冷器;0.022—0.032 m回热器;0.032—0.054 m加热器;0.054—0.154 m热缓冲管;0.154—0.174 m次水冷器;0.174—1.754 m谐振管)。
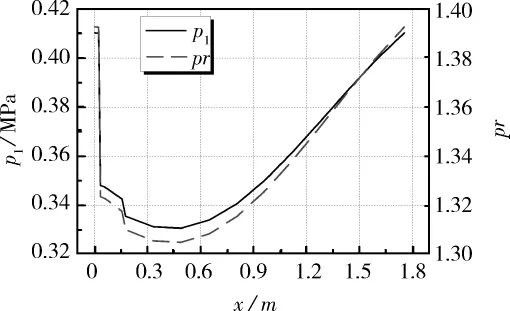
图2 压力波动幅值与压比沿程分布Fig.2 Distribution of pressure amplitude and pressure ratio
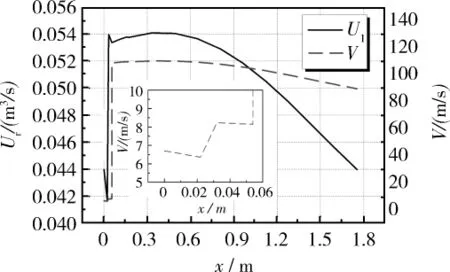
图3 体积流率与气体振荡速度沿程分布Fig.3 Distribution of volume flow rate and velocity
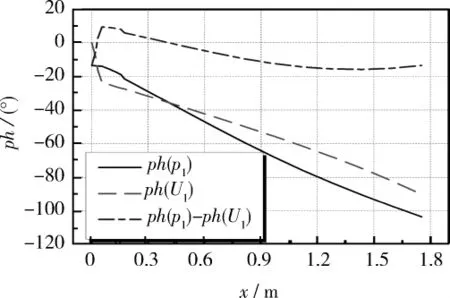
图4 相位沿程分布Fig.4 Distribution of phase
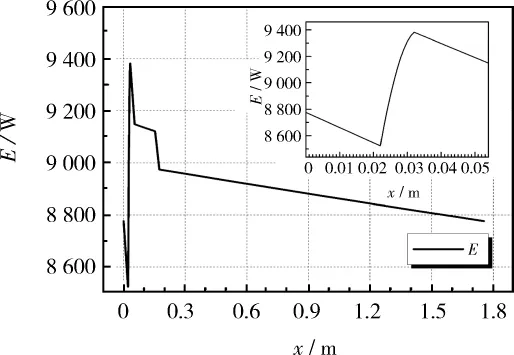
图5 声功率沿程分布Fig.5 Distribution of acoustic power
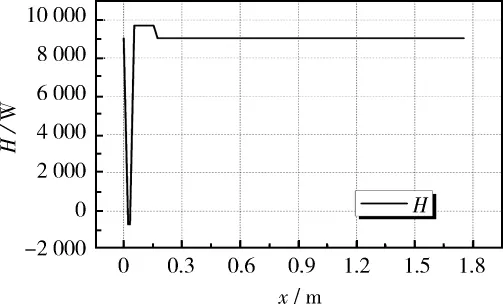
图6 总能流沿程分布Fig.6 Distribution of total energy
根据数值模拟计算结果,当系统工作时,其谐振频率f为133.51 Hz,在一个基本单元中,加热器加热量Qin为10 409.3 W时,回热器产生净声功率为857.2 W,热声转换效率达到8.2%,谐振管单元消耗声功率为663.5 W(图5)。
由图2可知,系统中压力波动幅值与压比的沿程波动不是很大,环路中形成一个较为理想的近纯行波声场,能够产生和传递更多的声功。主水冷器入口处压力波动振幅与压比均达到最大值,压力波动振幅最大值为0.41 MPa,压比最大值为1.39。
图3所示,系统中体积流率沿程波动幅度较小,最大体积流率与最小体积流率相差仅为13.0%。因此可以认为,变横截面积对系统中的体积流率影响不大。然而,在谐振管单元中,气体振荡速度高达89 m/s以上,而回热器单元中,气体振荡速度低于8.2 m/s。通过增大回热器单元的横截面积,有效降低了回热器中气体振荡速度,从而降低回热器的粘性损失,并且对系统的体积流率和声功率影响均较小。
从图4中可知,沿程压力波动与体积流率的相位差仅在-15.8°—9.5°的范围内,并在回热器内达到0°,声场中行波分量较大,相位比较理想,这将有利于声功的产生与传递。
综上,在环路声学共振4级行波热声发动机环路中,压力波动与体积流率接近同相,能够有效地产生和传递声功,具有潜在的高效率。增大回热器单元的横截面积有效降低了回热器内部气体振荡速度,从而降低了回热器内的粘性损失。回热器产生净声功率为857.2 W,热声转换效率达到8.2%,最大压比为1.39。
3.3 环路声学共振4级、8级、16级行波热声发动机性能对比
理论上来讲,可以将任意多个基本单元串接进环路中,通过调整每个基本单元中谐振管的长度来保证整个环路中谐振管单元的总长度一定,这样,对系统的谐振频率等性能参数的影响不大,但是更多的回热器单元却可以产生更多的声功,而且,在比例上来说,结构更加紧凑。基于以上考虑,本节着重对比了环路声学共振4级、8级以及16级行波热声发动机的性能。
在计算中,保持整个环路中所有谐振管单元的总长度一定。即4级行波热声发动机中,一个基本单元中的谐振管单元(包括热缓冲管100 mm、次水冷器20 mm和谐振管1 580 mm)的长度为1 700 mm,整个环路中所有谐振管单元的总长度为6 800 mm。那么在8级行波热声发动机中,保证整个环路中谐振管单元的总长度不变,一个基本单元中的谐振管单元长度即为850 mm,其中热缓冲管的长度100 mm、次水冷器长度20 mm,谐振管长度则为730 mm。同理,在16级行波热声发动机中,一个基本单元中的谐振管长度为305 mm。除了单个基本单元谐振管长度不同外,4级、8级、16级行波热声发动机的其它所有结构尺寸均相同。在整个闭合环路中,体积流率和压力波动的相位均分别变化了360°,因此对于4级行波热声发动机的一个基本单元,其进口和出口处的体积流率和压力波动的相位分别变化了90°。同理,8级行波热声发动机的一个基本单元,其进、出口处的体积流率和压力波动的相位分别变化了45°;16级行波热声发动机的一个基本单元,其进、出口处的体积流率和压力波动的相位分别变化了22.5°。计算中,对于各级行波热声发动机,平均工作压力pm均为2.5 MPa,主水冷器与次水冷器壁温tc1、tc2均为室温20℃,加热器壁温th固定为180℃。
图7—图12分别给出了压力波动幅值p1、压比pr、体积流率U1、相位角ph、声功率E以及总能流H沿装置长度x的沿程分布。
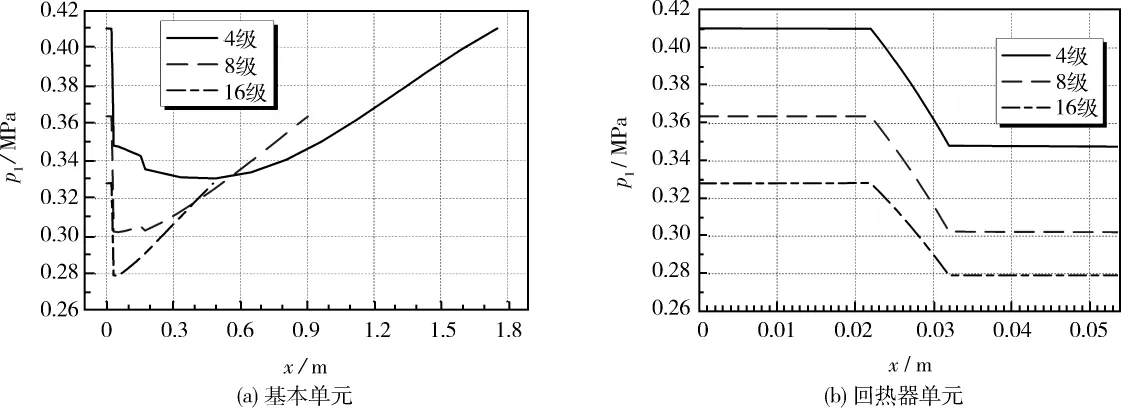
图7 压力波动幅值沿程分布(a)基本单元(b)回热器单元Fig.7 Distribution of pressure amplitude(a)for a basic unit(b)for a regenerator unit
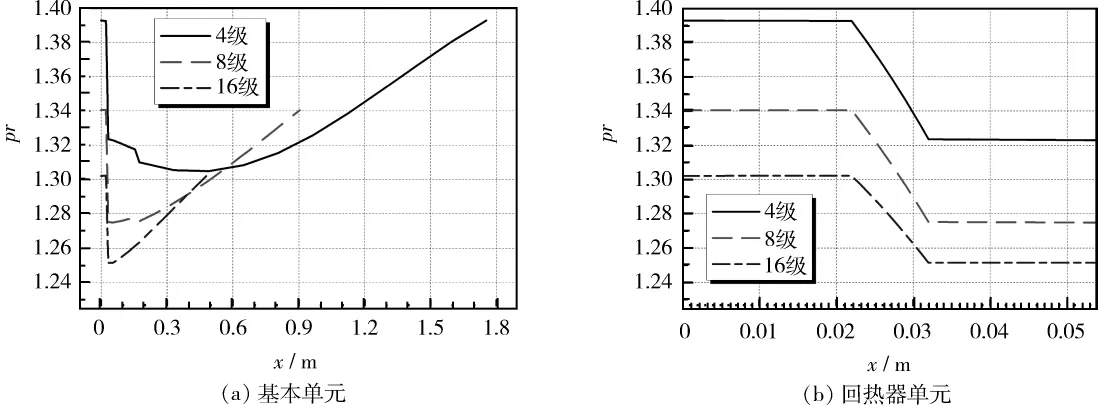
图8 压比沿程分布(a)基本单元(b)回热器单元Fig.8 Distribution of pressure ratio(a)for a basic unit(b)for a regenerator unit
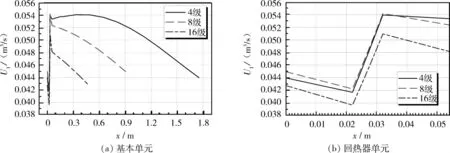
图9 体积流率沿程分布(a)基本单元(b)回热器单元Fig.9 Distribution of volume flow rate,(a)for a basic unit,(b)for a regenerator unit
根据数值模拟计算结果,4级、8级、16级行波热声发动机的谐振频率分别为133.51、120.15、102.29 Hz,依次略有降低。这可能是因为高级数行波热声发动机回热器内部阻力略大。
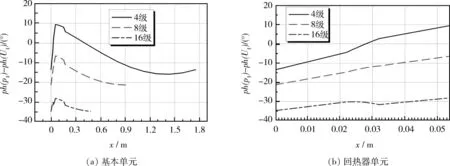
图10 压力波动与体积流率相位差沿程分布,(a)基本单元(b)回热器单元Fig.10 Distribution of phase delay,(a)for a basic unit,(b)for a regenerator unit
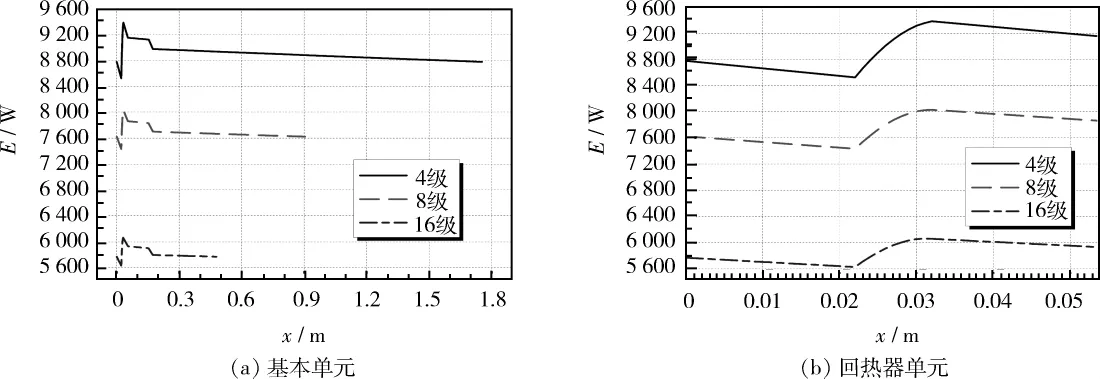
图11 声功率沿程分布(a)基本单元(b)回热器单元Fig.11 Distribution of acoustic power,(a)for a basic unit,(b)for a regenerator unit
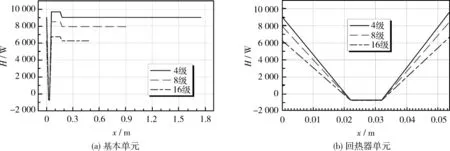
图12 总能流沿程分布(a)基本单元(b)回热器单元Fig.12 Distribution of total energy,(a)for a basic unit,(b)for a regenerator unit
在一个基本单元中,4级行波热声发动机加热器加热量为10 409.3 W时,回热器产生净声功率为857.2 W,热声转换效率为8.2%;8级行波热声发动机加热器加热量为9 281.6 W时,回热器产生净声功率为596.4 W,热声转换效率为6.4%;16级行波热声发动机加热器加热量为7 487.1 W时,回热器产生净声功率为431.8 W,热声转换效率为5.8%。因此,随着环路中串入的基本单元数量的增多,单个基本单元回热器产生的净声功率有所下降,热声转换效率也有所下降。这是因为回热器中阻力增大造成能量损失增加,以及相位分布变化。通过对高级数行波热声发动机回热器单元的结构尺寸以及回热器单元与谐振管单元的横截面积比的优化,可以预期达到更好的热声转换性能。图11b中,在回热器部分(0.022—0.032 m),4级、8级行波热声发动机回热器里的声功率是沿程上升的;而16级行波热声发动机的回热器中,声功率由5 628.7 W上升至最大值6 063.7W后又有所下降,至6 060.5 W。这也恰好说明了高级数行波热声发动机的回热器中能量损失对回热器产生声功率的影响。即便在目前的情况下,整个环路中回热器产生的总的净声功率,4级行波热声发动机为3 428.8 W;8级行波热声发动机为4 771.2 W;16级行波热声发动机为6 908.8 W,在整机结构尺寸变化不大的情况下,显然更高级数的行波热声发动机能够产生更多的净声功率。
由图7、图8可知,随着环路中串入的基本单元数量的增加,压力波动幅值与压比在总体上呈现减小的趋势,主水冷器入口处仍然是压力波动幅值与压比最大处。4级、8级、16级行波热声发动机最大压力波动幅值分别为0.410、0.364、0.328 MPa,最大压比分别为1.39、1.34、1.30。由于在高级数行波热声发动机系统中,总能流随着级数的增加,整体趋势上减小,因此压力波动也减小。在平均工作压力相同的情况下,压比与压力波动的变化趋势一致。
图9给出了4级、8级、16级行波热声发动机体积流率的沿程分布。从大体趋势上来说,更高级数的行波热声发动机,体积流率会有所降低。特别是在谐振管单元中的体积流率,会有较为明显的降低。由于谐振管的横截面积是一定的,因此,高级数行波热声发动机谐振管单元中气体振荡速度相对低级数行波热声发动机要低,因此,4级、8级、16级行波热声发动机谐振管单元内消耗的声功率也会降低。结合图11可知,单个基本单元中,4级、8级、16级行波热声发动机谐振管单元消耗的声功率分别为663.5、237.8、25.5 W;对于整个环路来说,4 级、8 级、16 级行波热声发动机谐振管单元消耗的总声功率分别为2 654.0、1 902.4、408.0 W。
由图10可知,在4级行波热声发动机中,压力波动与体积流率的相位差在-15.8°到9.5°之间;8级行波热声发动机压力波动与体积流率的相位差则在-21.2°到-6.4°之间;16级行波热声发动机压力波动与体积流率的相位差在 -34.7°到 -28.0°之间。由此可知,随着串入环路中基本单元数量的增多,系统声场中的驻波分量增大,而行波分量减小。但是总体上,声场中的行波分量仍占较大部分,声场仍是较为理想的。
由图12可知,4级、8级、16级行波热声发动机相比较,环路中串入的基本单元数目越多,整体上总能流就越少。但是回热器中的总能流却非常接近。
综上,环路声学共振4级、8级、16级行波热声发动机相比较,在环路中串接入更多的基本单元,会导致谐振频率、压力波动幅值、压比、体积流率、单个基本单元回热器产生净声功率、热声转换效率以及总能流的少量下降,同时会使得声场中的行波分量减小。但总体上,系统仍能达到较为理想的工作性能。通过对高级数行波热声发动机回热器单元的结构优化以及回热器单元与谐振管单元横截面积比的优化,能够使得高级数行波热声发动机的性能达到更佳状态,使环路声学共振多级行波热声发动机具有很好的应用前景。
4 结论
对环路声学共振多级行波热声发动机的工作机理进行了研究。首先分析了环路声学共振4级行波热声发动机无负载工作性能,环路中的声场行波分量较大,压力波动与体积流率相位差较小,具有潜在的高效率。增大回热器单元的横截面积有效降低了回热器内部气体振荡速度,从而降低了回热器内的粘性损失。一个基本单元回热器产生净声功率857.2 W,热声转换效率达到8.2%,最大压比为1.39。进一步对比了环路声学共振4级、8级、16级行波热声发动机的工作性能,计算结果表明,增加环路声学共振多级行波热声发动机的级数会导致谐振频率以及工作性能参数的略微降低,声场中的行波分量略有减少,但仍能获得较为理想的工作状态。同时高级数行波热声发动机整机产生净声功率增加,谐振管消耗声功率降低,相对结构更为紧凑。对高级数行波热声发动机结构的进一步优化将会使得高级数行波热声发动机的工作性能参数有所提高,这将是下一步的工作重点。
1 Ceperley P.A pistonless Stirling engine-the traveling-wave heat engine[J].J Acoust Soc Am,1979,66:1508-1513.
2 Yazaki A,Iwata T,Maekawa T,et al.Traveling Wave Thermoacoustic Engine in a Looped Tube [J].Physical Review Letters,1998,81(15);3128-3131.
3 Backhaus S,Swift G W.A Thermoacoustic Stirling Heat Engine[J].Nature,1999,399:335-338.
4 Luo Ercang,Ling Hong,Dai Wei.A High Pressure-ratio,Energy-focused Thermoacoustic Heat Engine with a Tapered Resonator[J].Chinese Science Bulletin,2005,50(3):284-286.
5 Kees de Blok.Novel 4-stage Traveling Wave Thermoacoustic Power Generator[C].Proceedings of ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting and 8th International Conference on Nanochannels,Microchannels,and Minichannels,Montreal Canada:2010.FEDSM-ICCMM2010-30527.
6 Ward B,Clark J,Swift G.Design Environment for Low-Amplitude Thermoacoustic Energy Conversion[M],DELTAEC Version6.2 Users Guide,2008.
7 Swift G W.Thermoacoustics:a unifying perspective for some engines and refrigerators[M].New York:AIP Press,2002.

