载人航天器舱内气体泄漏数值模拟分析

谢福寿 陈叔平 李存礼 陈 联 陈光奇

(1兰州理工大学石油化工学院 兰州 730050)

(2兰州物理研究所真空低温技术与物理国家重点实验室 兰州 730000)

1 引 言

从20世纪50年代至今，世界各航天大国在卫星、载人航天器、运载火箭等发射和运行过程中，大大小小的泄漏故障和事故屡屡发生，有的造成发射计划推迟，有的影响部分飞行任务，有的使工作寿命缩短，还有的导致星(箭)毁人亡。如20世纪60年代前苏联“联盟11号”飞船因密封舱漏气，舱内压力降低致使3名航天员丧生［1］。航天器检漏成为影响其正常发射的重要环节。龙伟、王纲明、宋金成建立了双密封结构泄漏过程的数学模型，从理论上解释了用氦质谱加压真空法测双密封结构产品漏率“缓慢升高”的现象［2］。刘阳、崔展鹏、孙冲等人建立了多级串联密封系统的数学模型，揭示了多级串联密封结构正压泄漏的漏率、漏量与泄漏时间关系的一般规律，通过三级密封系统泄漏的仿真计算实例和泄漏实验，验证了多级串联密封泄漏理论的正确性，并总结了多级串连密封泄漏规律的应用方法［3］。刘阳、崔展鹏、孙冲等人建立了双密封结构系统的数学模型，通过理论分析和数值计算，揭示了双密封结构系统正压泄漏的漏率、漏量与泄漏时间关系的规律及其影响因素的结论［4］。闫治平、黄淑英对不同的刚性物理漏孔进行了不同压力状态下的漏率试验，发现了漏率的函数关系。在试验的基础上，经理论分析，验证了其规律的正确性;同时，发现随着漏孔长度的减少而压力指数变大的规律［5］。

回顾学者们对舱内气体泄漏的研究，可以发现主要集中在气体泄漏中漏率方面，对泄漏状态和影响参数研究较少。本文拟提出内外升压法，利用基于Simple算法的Fluent软件数值模拟载人航天器舱内气体泄漏状态，分析气体泄漏过程中影响参数;同时，引入一个无量纲参数气体泄漏因子Fs，为判定载人航天器舱内气体泄漏是否达标提供一定的理论依据。

2 舱内气体泄漏数值模拟

2.1 几何模型的建立

采用前处理软件Gambit进行二维建模，忽略结构的影响，建立的几何模型如图1所示。其中A-I段、J-B段为内舱壁，face1为镀铝薄膜层，face2为微流星体防护层，face3和face5为外舱壁，I-J段和N-M段为泄漏小孔，face6为舱外大气。

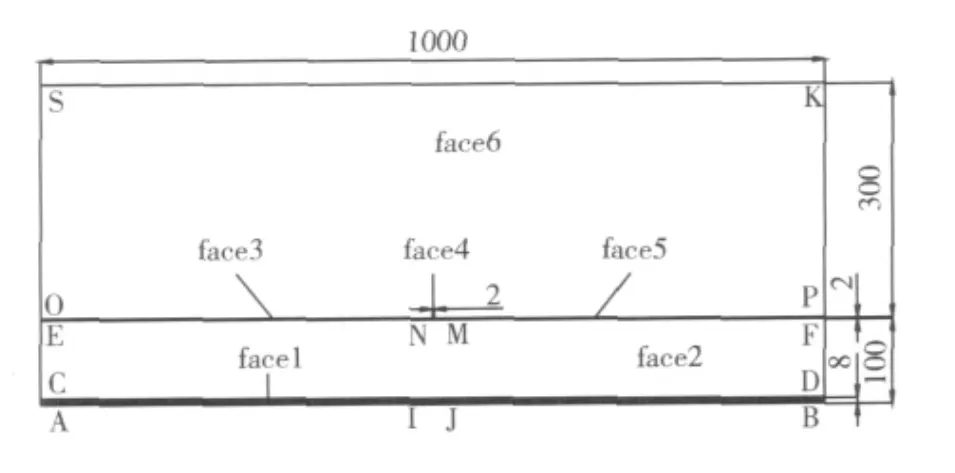
图1 舱内二维几何模型Fig.1 2D geometric model of cabin

2.2 网格划分

采用前处理软件Gambit进行整体划分，生成结构化网格，如图2所示。其中face1、face2、face3、face4和face5网格为1 mm×0.5 mm，face6网格为1 mm×1 mm。

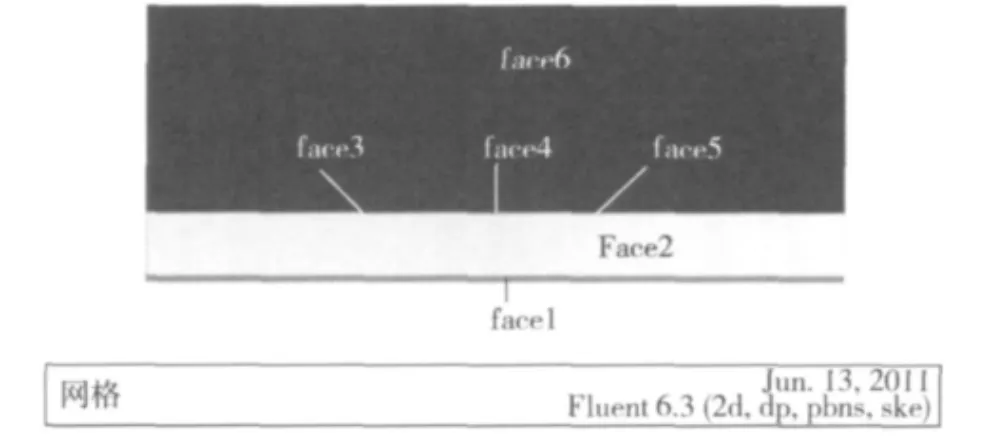
图2 结构化网格图Fig.2 Structured grid

2.3 多孔介质模型

采用多孔介质模型来处理镀铝薄膜层内的流动。由式(1)和式(2)可知，粘性阻力系数 α=0.53×1011，惯性阻力系数 C2=0.7。

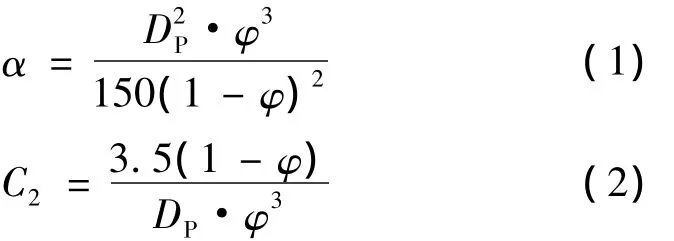
式中:DP为粒子的平均直径;φ为孔隙率，其定义为微小空隙总体积与镀铝薄层总体积之比。

2.4 边界条件及流动区域设置

由于在真空状态下，无法进行数值模拟，现采用内外舱同时升高0.1 MPa来进行数值模拟。

(1)根据图1所示，边界条件设置如下:

进口压力(pressure-inlet):I-J段，0.2 MPa;

出口压力(pressure-outlet):A-C段、C-E段、O-S段、S-K 段、K-P 段、F-D 段、D-B 段，0.1 MPa;

舱内部(interior):C-D段、N-M段;

舱壁(wall);

其余为壁边界。

(2)根据图1所示，流动区域设置如下:

流动区域(Fluid):face1、face2、face4、face6;

实体区域(Solid):face3、face5。

2.5 结果分析

2.5.1 收敛性与稳定性

如图3所示，计算结果中残差的收敛情况比较理想。在迭代443次后，计算收敛，收敛标准为1×10－3。

2.5.2 流场中的压力分布

图4反映了泄漏过程中的压力分布状态，不同的压力等高线用不同的颜色表示。从图4可看出，流场中最大压力为1.99×105Pa和最小压力为1.0×105Pa。由图4可知，在镀铝薄膜层(在Fluent中用多孔介质模型来处理)内，由于存在粘性阻力和惯性损失，使压力分布比入口处的明显减弱;微流星体防护层与镀铝薄膜层的压力分布基本一致，是由于刚开始镀铝薄膜中的空气进入防护层，随后防护层中的气体回流到镀铝薄膜中，最终系统达到稳态状态，使压力分布基本保持一致;在小孔出口处，压力呈扇形分布，并逐渐减弱至0.1 MPa。

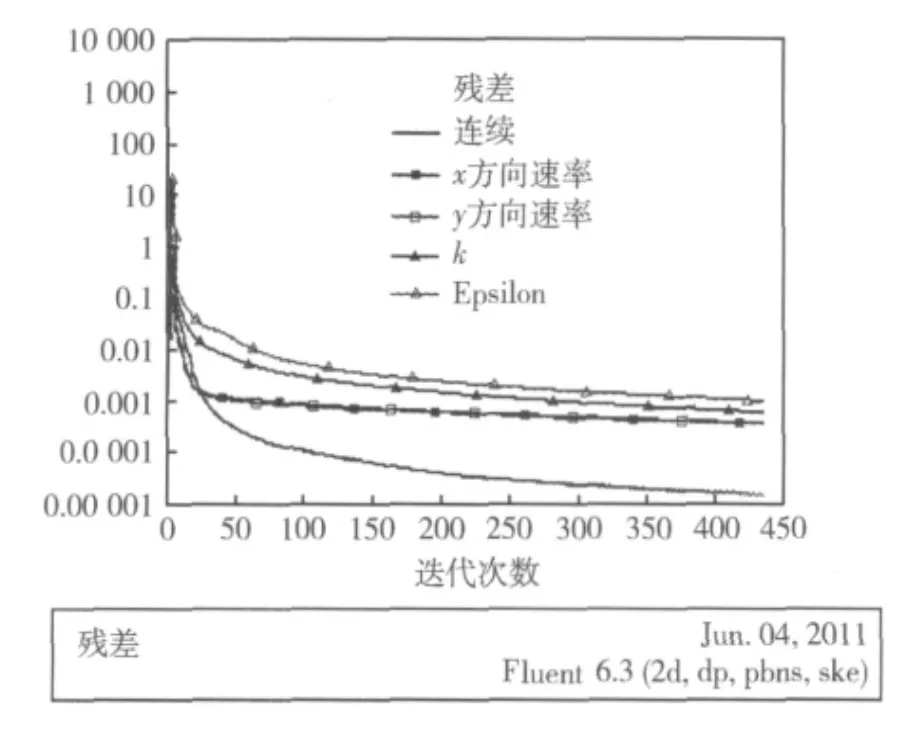
图3 2 mm孔径残差监测变化曲线Fig.3 2 mm aperture residual detection curve

图4 2 mm孔径流场中压力分布图Fig.4 2 mm aperture flow field pressure distribution chart

2.5.3 沿t-y线压力变化曲线

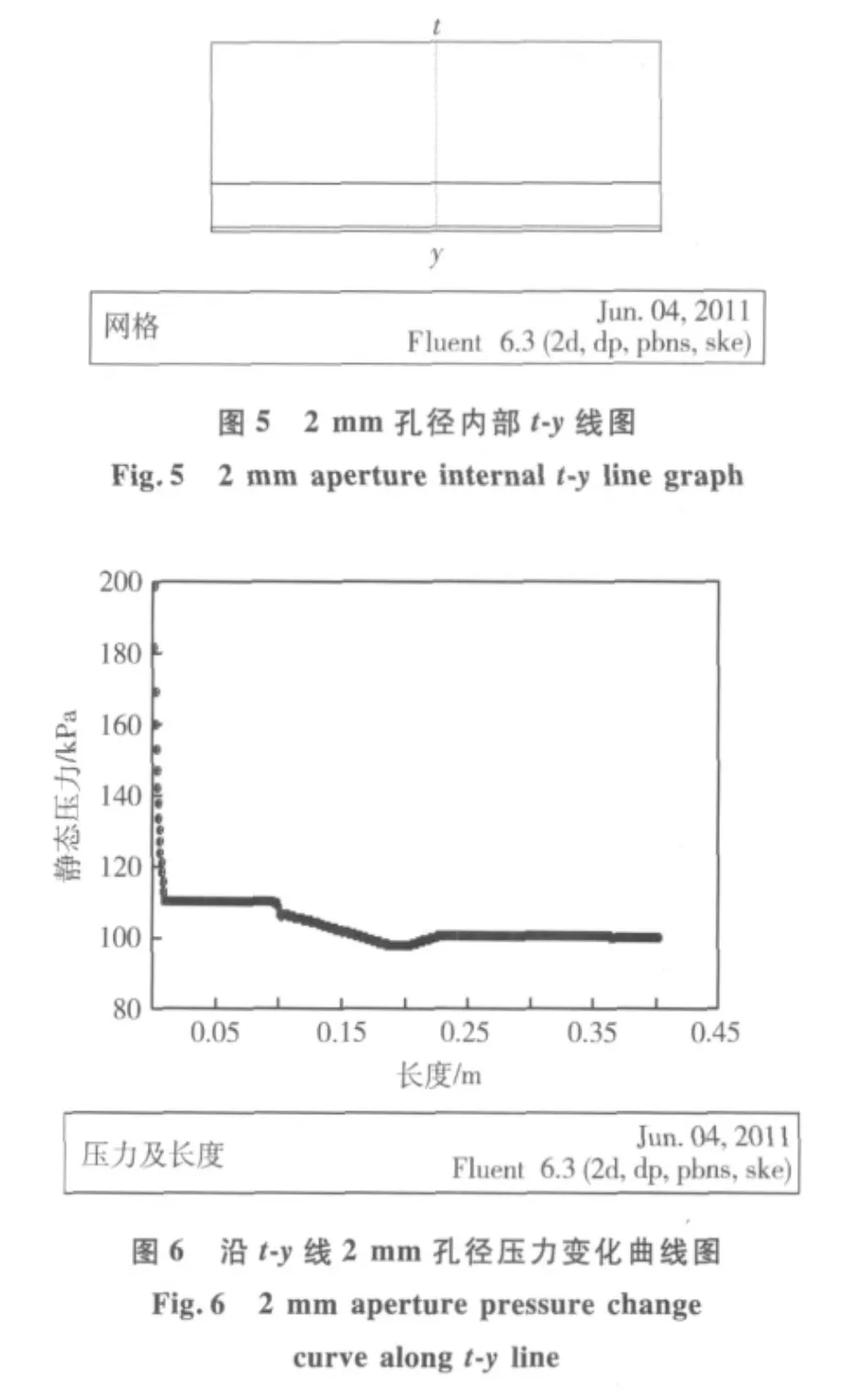
为了更加清楚地描述流场中小孔入口到出口处的压力变化规律，画了一条孔径内部t-y线、一条沿ty线2 mm孔径压力变化曲线图，分别如图5、图6所示。由图6可知，沿着内部t-y线，在镀铝薄膜层内由于存在粘性阻力系数和惯性阻力系数，使压力值迅速从0.2 MPa降到0.11 MPa左右;在系统稳态时，镀铝薄膜层和微流星体防护层中的压力分布基本保持一致;在小孔出口处，压力分布降低，逐渐趋于外界0.1 MPa压力。

2.5.4 沿m-n线压力变化曲线

为了更加清楚地描述流场中微流星体防护层内横向压力变化规律，画了一条内部m-n线、一条沿mn线2 mm孔径压力变化曲线，分别如图7、图8所示。由图8可知，沿内部m-n线，在系统处于稳定时，微流星体防护层内横向压力基本不变，保持在0.11 MPa左右。

图7 2 mm孔径内部m-n线图Fig.7 2 mm aperture internal m-n line graph

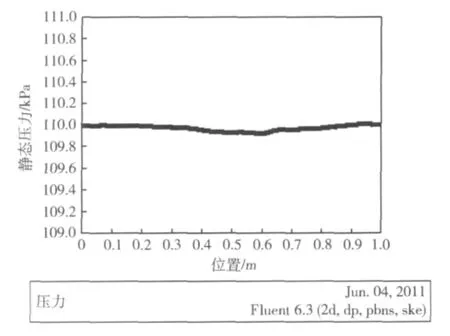
图8 沿t-y线2 mm孔径压力变化曲线图Fig.8 2 mm aperture pressure change curve along t-y line

2.6 气体泄漏因子Fs

为了判定载人航天器舱内气体泄漏大小，引入气体泄漏因子Fs概念，其定义为:泄漏小孔出口处压力与泄漏小孔入口处压力之比，如式(3)。

气体泄漏因子Fs以无量纲理论为基础，从本质上反映了气体泄漏的大小，即Fs越大，气体泄漏越大，反之亦然。

由Fluent软件可以分别计算出小孔孔径D=2 mm处入口和出口的总压力。在图1中，小孔入口I-J段总压力为1.88×105Pa，小孔出口N-M段总压力为1.06×105Pa。由式(3)可知，气体泄漏因子Fs为 56.4%。

3 影响参数分析

载人航天器舱内气体泄漏主要影响参数包括:小孔孔径D、镀铝薄膜层的材料孔隙率φ、镀铝薄膜层厚度h和微流星体或空间碎片入射角度θ。

3.1 小孔孔径D

微流星体或空间碎片在太空高速飞行时，会和在轨载人航天器发生碰撞，甚至直接击穿载人航天器，形成一个小孔孔径D，发生舱内气体泄漏，故小孔孔径是由在太空飞行的微流星体或空间碎片决定的。

为了更好的分析小孔孔径对气体泄漏的影响，在前处理软件Gambit建模时，对小孔孔径进行修改，其它模拟条件设置不变，现假定以下3种情况:D=1 mm，D=2 mm，D=4 mm。

3.1.1 小孔孔径为1 mm

小孔入口I-J段总压力为1.914×105Pa，小孔出口N-M段总压力为1.004×105Pa，根据式(3)，气体泄漏因子Fs为52.5%。

3.1.2 小孔孔径为4 mm

小孔入口I-J段总压力为1.815×105Pa，小孔出口N-M段总压力为1.058×105Pa，根据式(3)，气体泄漏因子Fs为58.3%。

由以上分析可知，当小孔孔径分别为D=1 mm，D=2 mm(由1.6节可知)，D=4 mm时，气体泄漏因子分别为 Fs=52.5%、Fs=56.4%、Fs=58.3%，可以看出，随着小孔孔径D的不断增加，气体泄漏因子也不断增加。

3.2 镀铝薄膜层的材料孔隙率φ

镀铝薄膜层小孔孔径和内部结构分布直接决定了气体穿过镀铝薄膜层的渗透能力，而在Fluent软件中把镀铝薄膜层当作多孔介质模型来处理，相当于人为地对气体设置一个粘性阻力系数和惯性阻力系数，故把孔隙率φ作为影响因素来分析，对于了解气体穿过镀铝薄膜层渗透能力的影响具有一定的参考价值。

在Fluent软件中，其它设置条件不变，现假定以下3种情况，孔隙率分别为φ =0.05，φ =0.1，φ =0.15时进行数值模拟，来观察多孔介质中的孔隙率对气体泄漏因子的影响。

3.2.1 孔隙率为 φ =0.05

小孔入口I-J段总压力为1.89×105Pa，小孔出口N-M段总压力为1.05×105Pa，根据式(3)，气体泄漏因子Fs为55.6%。

3.2.2 孔隙率 φ =0.15

小孔入口I-J段总压力为1.499×105Pa，小孔出口N-M段总压力为1.048×105Pa，根据式(3)，气体泄漏因子Fs为69.9%。

由以上分析可知，当镀铝薄膜层的材料孔隙率分别为 φ =0.05，φ =0.1(由1.6 节可知)，φ =0.15时，气体泄漏因子分别为 Fs=55.6%，Fs=56.4%，Fs=69.9%，故可以看出，随着多孔介质孔隙率φ的不断增加，气体泄漏因子Fs不断增大。

3.3 镀铝薄膜层厚度h

为了了解镀铝薄膜层厚度h对气体泄漏因子Fs的影响，现假定以下3种情况，镀铝薄膜层厚度分别为h=4 mm，h=8 mm和h=15 mm时进行数值模拟，来观察镀铝薄膜层厚度对气体泄漏因子的影响。

3.3.1 镀膜薄膜层厚度h=4 mm

小孔入口I-J段总压力为1.85×105Pa，小孔出口N-M段总压力为1.05×105Pa，根据式(3)，气体泄漏因子Fs为56.8%。

3.3.2 镀膜薄膜层厚度h=15 mm

小孔入口I-J段总压力为1.9×105Pa，小孔出口N-M段总压力为1.05×105Pa，根据式(3)，气体泄漏因子Fs为55.2%。

由以上分析可知，当镀铝薄膜厚度分别为h=4 mm，h=8 mm(由1.6 节可知)，h=15 mm 时，气体泄漏因子分别为 Fs=56.8%，Fs=56.4%，Fs=55.2%，故可以看出，随着镀铝薄膜层厚度h的不断增加，气体泄漏因子Fs不断减小。

3.4 微流星体或空间碎片入射角度θ

为了了解微流星体或空间碎片入射角角度θ对气体漏率的影响，假设其它模拟条件不变，现假设以下3种情况，入射角角度分别为θ=0°(垂直入射)，θ=44.6°(N-M线段向x正方向偏离50 mm形成的夹角)，θ=74.6°(N-M线段向x正方向偏离150 mm形成的夹角)。

3.4.1 入射角度 θ=44.6°

小孔入口I-J段总压力为1.87×105Pa，小孔出口N-M段总压力为1.016×105Pa，根据式(3)，气体泄漏因子Fs为54.3%。

3.4.2 入射角度 θ=74.6°

小孔入口I-J段总压力为1.88×105Pa，小孔出口N-M段总压力为1.01×105Pa，根据式(3)，气体漏率Fs为53.7%。

由以上分析可知，当入射角角度分别为θ=0°(由 1.6 节可知)、θ=44.6°、θ=74.6°时，气体泄漏因子分别为 Fs=56.4%、Fs=54.3%、Fs=53.7%，故可以看出，随着入射角度θ的不断增加，气体泄漏因子Fs不断减小。

4 结束语

基于Simple算法的Fluent软件模拟了载人航天器舱内气体泄漏时的压力，在此基础上，建立了不同影响参数的数值模型，分析了影响载人航天器舱内气体泄漏的主要参数，并得到以下结论:

(1)沿着 t-y线(纵坐标)，0.2 MPa压力逐步降低，在镀膜薄膜层内压降变化较为明显，在微流星体防护层内，压降基本保持不变，在出口处呈扇形向四周扩散，逐渐降至0.1 MPa;

(2)沿着m-n线(横坐标)，在系统达到稳态时，压力呈一条水平线，基本保持稳定;

(3)小孔孔径越大，气体泄漏因子越大;

(4)对镀铝薄膜层的材料结构进行优化，使其孔隙率变小，气体泄漏因子降低;

(5)增加镀铝薄膜层厚度，气体泄漏因子降低;

(6)引入气体泄漏因子Fs概念，来判定舱内气体泄漏大小，即气体泄漏因子Fs越小，舱内气体泄漏越小，反之亦然，为在轨载人航天器判定舱内气体泄漏大小提供了一定的理论依据。

1 吴国兴.空间站和航天飞机［M］.北京:中国宇航出版社，2003.

2 龙 伟，王纲明，宋金成.双密封结构泄漏过程浅析［J］.真空与低温，2001，7(3):184-187.

3 刘 阳，孙 冲，崔展鹏，等.多级串联密封系统泄漏规律及应用研究［J］.宇航学报，2005，26(4):476-484.

4 刘 阳，崔展鹏，孙 冲，等.双密封结构的泄漏理论及其应用研究［J］.中国空间科学技术，2003(6):38-46.

5 闫治平，黄淑英.漏率与压力关系的研究［J］.中国空间科学技术，1999(4):42-47.