环境压力对低温容器蒸发流量的理论分析和试验验证

刘惠民 冯慧华

(上海船用柴油机研究所 上海 201203)

1 引 言

蒸发率是评定低温容器绝热性能的一项重要指标。影响蒸发率的因素很多，比如环境压力、环境温度、充满率等。随着低温容器的绝热性能的不断提高，环境因素对蒸发流量的影响程度也越明显。由于在实际测试中，无法对环境因素尤其是环境压力的变化进行有效控制，造成瞬时蒸发流量呈现较为明显的波动。对此现象，前人作了不少相关工作［1-5］，指出环境条件的变化会对蒸发量产生较大的影响，同时从气化潜热以及内外压差两方面对蒸发流量的影响进行了定性说明，但并未进行深入的量化分析。

基于低温容器内气、液两相热力平衡的假设，建立了瞬时蒸发流量与环境温度、压力之间的关系。定量分析了容器在不同漏热、不同装载量情况下环境压力变化对于蒸发流量的影响程度，并与35 m3高真空多层绝热液氮低温容器蒸发流量测试试验结果进行了对比，验证了计算结果的合理性和有效性。

2 蒸发量计算模型的建立

2.1 计算模型及假设

热力学模型如图1所示。定义在一个任意时刻t时容器内所有液体所含的空间为控制容积，系统边界由气、液相分界面以及液体与容器内壁面的边界组成(图1虚线框)。在模拟计算中，作出如下假设:

(1)气、液相平衡;

(2)气、液相温度均匀一致，无温度分层;

(3)忽略沿高度方向压力的变化;

(4)忽略蒸发气体的动能;

(5)系统压力为液相饱和压力，且与环境压力一致;

(6)容器为刚性，没有形变。

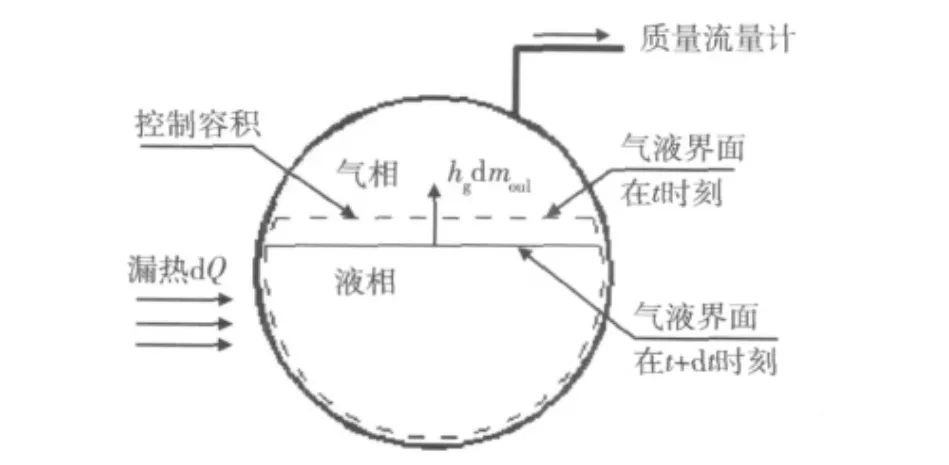
图1 液氮低温容器蒸发计算数学模型Fig.1 Schematic drawing of LN2boil-off model

2.2 数学方程

能量守恒方程:

系统总内能:

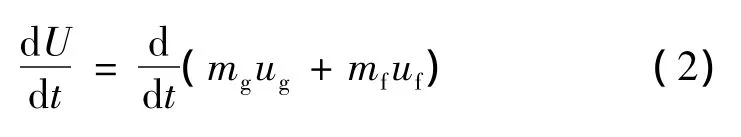
式(1)、式(2)中:U为系统总内能，kJ;Q为系统漏热，kJ;hg为气体比焓，kJ/kg;mout、mg、mf分别为蒸发流量、气体质量、液体质量，kg;ug、uf分别为气体、液体比内能，kJ/kg。

质量守恒方程:

式(3)—式(5)中:ρg、ρf分别为气体、液体密度，kg/m3;Vg、Vf分别为气体、液体体积，m3。

容器为刚性:

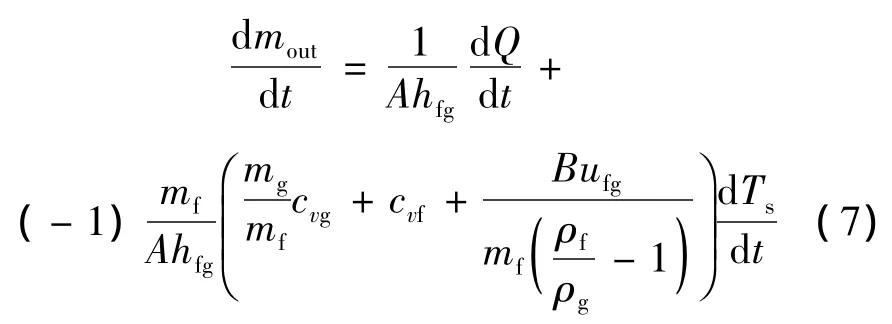
其中:

由Clausius-Clapeyron方程可以得到气相饱和温度与饱和压力关系:

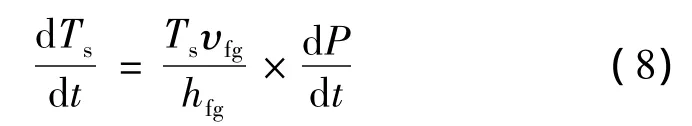
式(7)、式(8)中:υfg=υg－ υf，υg、υf分别为气体、液体的比体积;hfg=hg－hf为蒸发潜热，hg、hf分别为气体、液体的比焓;ufg=ug－ uf，kJ;cvg、cvf分别为饱和蒸气、饱和液体的定容比热容，kJ/(kg·K);Ts为系统饱和温度，K;P为系统压力(环境压力)。式(7)、式(8)表明，通过系统漏热和环境因素(温度和压力)可以计算得到瞬时蒸发流量。

2.3 简化和讨论

在进行蒸发率测试过程中，容器的充满率一般比较高，液体质量远大于气体质量，即mf≫mg;同时在大气压附近时，因此式(7)可以简化为:

通过高真空多层绝热的漏热［6］可以用式(10)表示:

系统的总漏热:

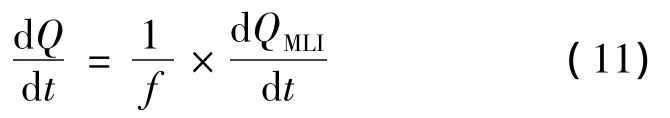
将式(8)、式(10)、式(11)代入式(9)，整理可得:

其中:

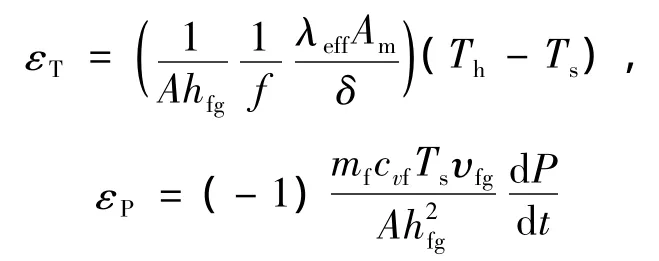
式中:QMLI为通过绝热层的漏热，kJ;λeff为高真空绝热层的表观导热系数，mW/(m·K);δ为绝热层厚度，mm;Am为多层绝热的等效传热面积，m2;f为通过多层绝热的漏热占系统漏热的比例。

由式(12)可知，瞬时蒸发流量可以分为两部分:一部分是环境温度引起的蒸发流量εT，由环境温度和液体饱和温度差Th－Ts、饱和热物性以及罐体绝热性能决定，数值为正，起到加速蒸发作用;另一部分是蒸发流量εP，由环境压力P、饱和热物性、液体量mf以及环境压力变化率dP/dt决定，数值为负，起到抑制蒸发作用。当环境压力升高后，液体饱和温度也将升高，由于液体量大，液体升高温度所需要的热容量也将增大，从而使得用于蒸发的热量相应减少，造成蒸发量变小。

由式(9)可以得到:

图2、图3分别给出了低温容器在不同漏热、不同装载量两种情况下，环境压力变化对于瞬时蒸发流量的影响程度。从图中可以看出，容器内液体质量越大，漏热量越小，那么环境压力变化的影响就越重要。如果要忽略环境压力对蒸发流量的影响(D≤0.01)，对于容器在额定装载量、漏热200 W的情况，环境压力变化率必须低于1.0×10－3Pa/s才能满足;即使容器装载量只有20%(约5 000 kg)的情况，环境压力变化率也至少要低于0.5×10－3Pa/s，然而实际上在室外，环境压力的变化在绝大部分时间里是远高于此值，因此在计算中有必要考虑环境压力的变化所产生的影响。

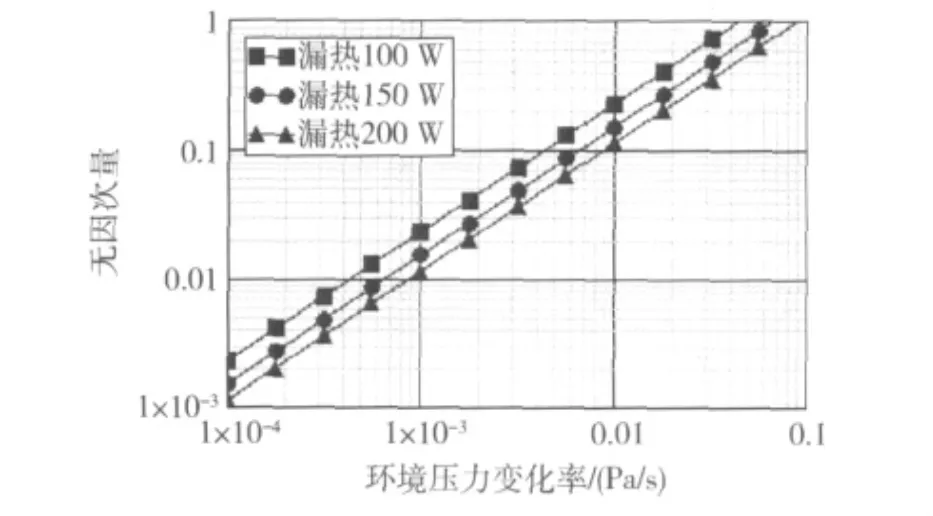
图2 对于装载量95%(约25 000 kg)的液氮容器在环境压力1×105Pa时，无因次量与漏热量、环境压力变化率的关系Fig.2 Calculated dependence of dimensionless parameter D with different heat leak and variations in atmospheric pressure with 95%fill-rate of LN2at 1×105Pa of pressure

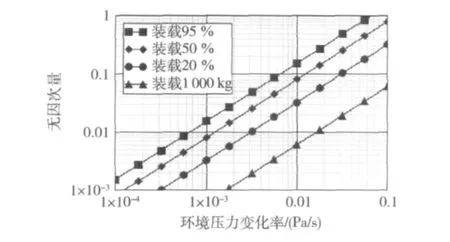
图3 对于漏热量150 W的液氮容器在环境压力1×105Pa时，无因次量与装载量、环境压力变化率的关系Fig.3 Calculated dependence of dimensionless parameter D with different fill-rate and variations in atmospheric pressure with 150 W heat leak at 1×105Pa of pressure

3 试验验证

3.1 试验系统及流程

对35 m3高真空多层绝热低温容器分别在2个不同地点进行了蒸发率测试，试验系统如图4所示。质量流量计采用美国FCI公司产GF92型热式气体质量流量计，量程为0.4—9.4 kg/h，精度为全量程1%。试验流程按照国家标准GB/T18443-2010《真空绝热深冷设备性能试验方法》。

图4 蒸发率试验系统图1.低温容器;2.泄放阀;3.加热器;4.质量流量计。Fig.4 Configuration of devices during LN2boil-off measurement

3.2 试验结果及与计算结果对比分析

图5 、图6为在不同测试地点进行蒸发率试验时得到的瞬时流量和环境压力曲线。由图可见，瞬时蒸发流量呈现不断波动的现象，且最大流量与最小流量相差可达50%以上。虽然在测试地点一，蒸发流量与环境压力在一定程度上具有反相关系的规律性，但是在测试地点二并不如此，说明存在其它影响流量波动的重要因素。

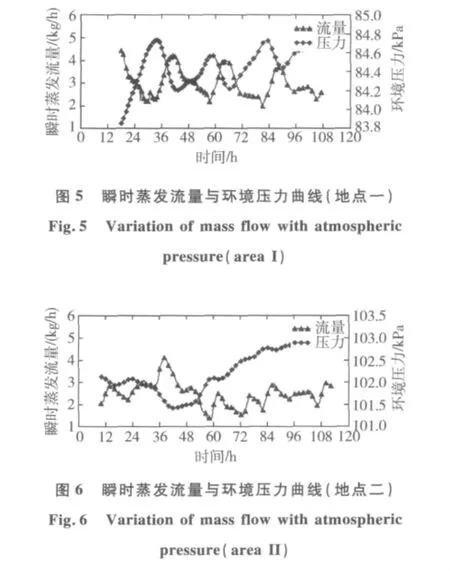
图7、图8给出了式(12)中分别由环境温度和环境压力变化引起的瞬时蒸发流量与试验结果的对比。从图中可以看出，由环境温度引起的流量曲线波动较小，因为液氮热物性以及高真空多层绝热的容器漏热量对环境温度的变化较不敏感。而由环境压力变化引起的流量曲线波动明显，且与试验的流量变化趋势基本一致，虽然实际环境压力变化并不明显，但是由于容器内液体量较大，起到了放大波动的效果。

图7 分别由环境温度、环境压力变化引起的瞬时蒸发流量计算结果与试验结果对比(地点一)Fig.7 Comparison of experimental and calculated results for mass flow considering atmospheric temperature and pressure change rate respectively(area I)

图8 分别由环境温度、环境压力变化引起的瞬时蒸发流量计算结果与试验结果对比(地点二)Fig.8 Comparison of experimental and calculated results for mass flow considering atmospheric temperature and pressure change rate respectively(area II)

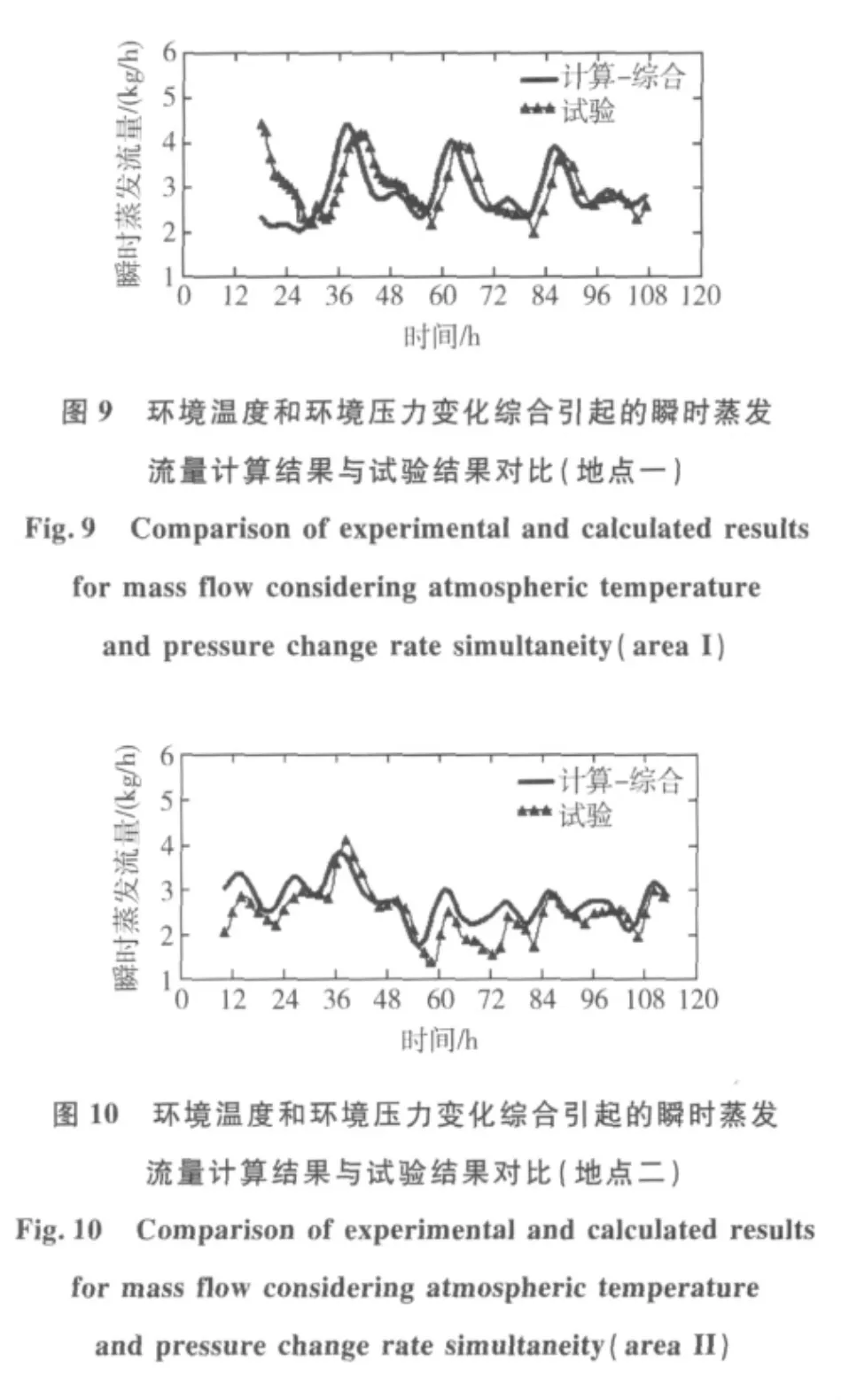
图9 、图10给出了环境温度和环境压力变化两者综合产生的瞬时流量曲线。从图中可以看出，与试验结果在数值以及变化趋势上吻合程度较好，验证了假设和模型的合理性和有效性。另外，试验蒸发流量与计算的差别体现在两个方面:一是试验流量波动响应要比计算的波动稍慢，这是由于试验系统的流阻对容器内外压力的平衡建立速度产生了延迟的效果，造成液体实际蒸发时间上慢于计算。二是两者数值上的差别，这主要是因为模型未考虑实际液体存在温度分层的情况。

4 结 论

建立了计算低温容器瞬时蒸发流量的热力学模型，分析了环境压力变化对蒸发流量的影响，对35 m3高真空多层绝热液氮低温容器在两个地点进行了蒸发量试验，试验结果很好地验证了计算模型的合理性和有效性，并得出以下结论:

(1)瞬时蒸发流量的波动主要是受到环境压力变化的影响，环境温度仅仅影响的是蒸发流量的平均值。容器漏热越小，液体量越多，那么环境压力变化的影响就越明显。

(2)试验系统的流阻会对容器内外压力的平衡建立速度产生影响，造成容器内部压力响应慢于环境压力的变化，表现为实际流量变化在时间上稍慢于计算结果。

(3)可以在试验系统出口增加一个稳压装置，削弱或补偿环境压力变化所产生的影响。

1 Pavel Hanzelka，Jaroslav Horky.Problems of measurement of the helium boil off rate of tomographic magnets［J］.Cryogenics，1999(39):647-649.

2 李 娟，汪荣顺，于耀华.低温绝热气瓶压力对日蒸发率的影响规律研究［J］.低温与特气，2005，23(6):8-11.

3 陈喜海，汪荣顺.低温容器蒸发率试验及蒸发量波动分析［J］.低温工程，2010(2):42-45.

4 李 阳，汪荣顺，王彩莉.环境压力对低温绝热气瓶蒸发率修正的试验研究［J］.低温与超导，2010，38(9):6-8.

5 谢高峰，汪荣顺.低温容器蒸发率试验及影响因素分析［J］.第八届全国低温工程大会暨中国航天低温专业信息网2007年度学术交流会议论文集，北京:2007.30-33.

6 符锡理.真空多层绝热理论研究和传热计算［J］.低温工程，1989(2):1-11.