连续旋转爆轰三维流场的数值模拟

潘振华，范宝春，张旭东，归明月

(南京理工大学 瞬态物理国家重点实验室，江苏 南京210094)

0 引言

燃烧有两种方式:爆燃和爆轰。相比之下，爆燃是定压条件下的燃烧，爆轰则是接近定容条件下的燃烧。相同条件下，爆轰的热力学效率比爆燃高，因此，爆轰发动机的研究受到广泛的关注。

爆轰发动机通常分为3 类:1)斜爆轰发动机(ODWE)，要求发动机的来流速度高于燃料的爆轰速度;2)脉冲爆轰发动机(PDE)，通过在燃烧室形成高频脉冲爆轰波，频率为1 000 Hz 或更高，产生相对稳定的推力［1］;3)旋转爆轰发动机(RDE)，其主要特点是爆轰波在环形的燃烧室连续旋转，从而产生稳定的推力，如图1所示。

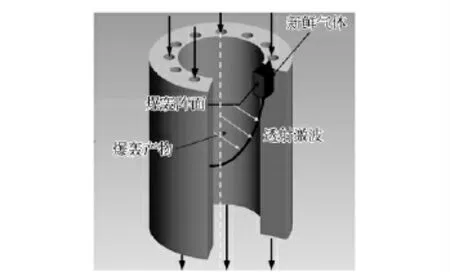
图1 旋转爆轰发动机流场示意图Fig.1 Schematic diagram of flow field in a rotating detonation engine

旋转爆轰的研究始于1959年，文献［2－3］进行了实验研究，首次在充有乙炔或乙烯预混燃气的圆管内形成短暂的旋转爆轰。随后，文献［4－8］利用不同的燃料(例如氢气、丙烷、丙酮、煤油等)，在各种大小和形状不同的燃烧室内(例如环形燃烧室、带扩张管道的环形燃烧室等)形成旋转爆轰。研究发现，连续旋转爆轰的可持续性与预混可燃气体的压力、燃烧室的形状尺寸、周围环境等密切相关。混合高度均匀时，其爆速和结构都能保持一定的稳定。文献［9］在GH2－LO2和LHC－GO2的两相预混系统中，得到了旋转爆轰。文献［10］用乙炔、氧气为预混气、在燃烧室内得到稳定传播的旋转爆轰，其波速与理论C－J 值较符合。文献［11］尝试用C/SiC混合材料进行旋转爆轰实验，评估了该材料对旋转爆轰波形成条件的影响。

旋转爆轰的数值模拟也取得了一定的进展。文献［12］对氢/氧预混燃料中的旋转爆轰进行了平面二维计算，分析了爆轰波的传播机理。文献［13］基于二维Euler 方程，模拟了旋转爆轰发动机的流场，讨论了入气口的参数、燃烧室尺寸等对燃烧室内爆轰波的影响。文献［14］通过二维数值模拟，获得了连续爆轰管头部的胞格结构，并对推进性能进行了分析。

本文基于考虑基元化学反应的Euler 方程，对氢气－空气预混气的旋转爆轰进行了数值模拟，讨论爆轰波—激波组合的结构特征、旋转爆轰诱导的三维流场和侧向稀疏波对化学反应区结构的影响。

1 物理模型和计算方法

贴体坐标中，带化学反应的Euler 方程:

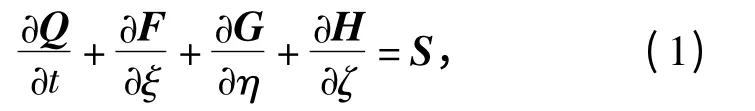
式中:Q 表示守恒变量;F、G 和H 分别表示ξ、η 和ζ 方向的对流通量;S 表示化学反应源项。这些矢量

本文采用分裂格式，将控制方程中的对流项和化学反应项分开处理。

守恒变量Q 的求解可表示为

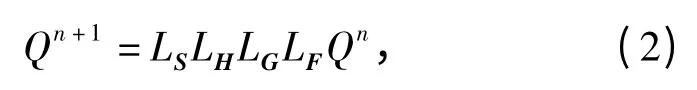
式中L 为操作算符。由于计算流场中存在激波这样的强间断，因而流场的计算要能反映间断(波)的传播特性。本文对流项采用二阶精度的波传播算法［15］，第n+1 时刻的解为

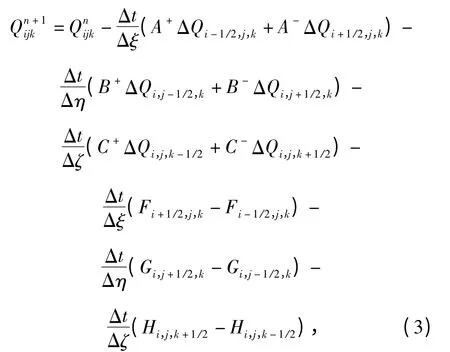
式中:右端第1 项表示第n 时刻的值;第2～第4 项分别表示ξ、η 和ζ 方向的一阶迎风项;第5～第7项分别表示ξ、η 和ζ 方向的二阶修正项，它保证了格式的二阶精度。下面以ξ 方向为例，一阶迎风格式用Roe 格式求解，二阶修正项可以表示为

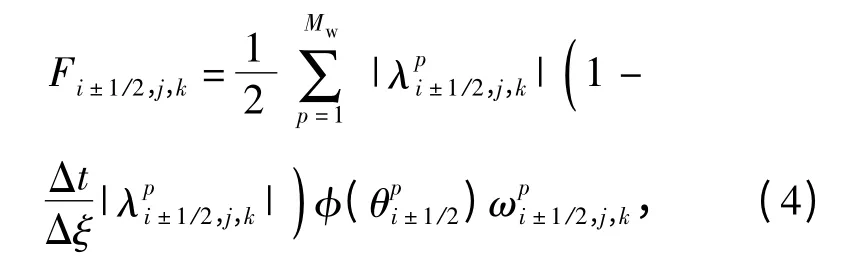
式中:Mw是波的个数;λ 是Roe 格式中系数矩阵的特征值;ωp表示通过第p 道波后的跳跃值，见文献［15］;φ(θpi±1/2)为限制函数，目的是为了消除间断附近的数值振荡，本文采用了Superbee 限制函数形式:

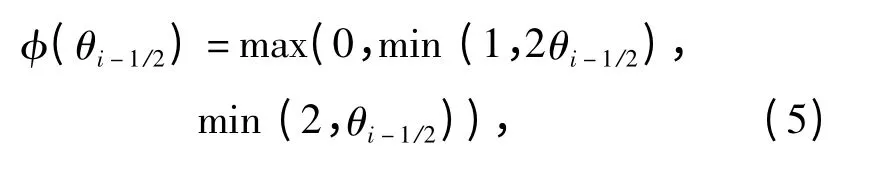
式中:

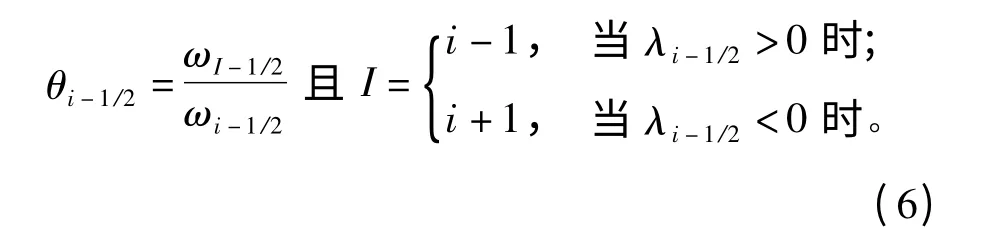
η、ζ 方向的二阶修正项也采用类似ξ方向的形式。

由于化学反应过程中不同反应物质的特征时间相差很大，因此会带来“反应刚性”的计算问题，故在该过程中采用基于隐式Gear 格式的LSODE 程序计算。

时间导数项采用2 步Runge－Kutta 法:

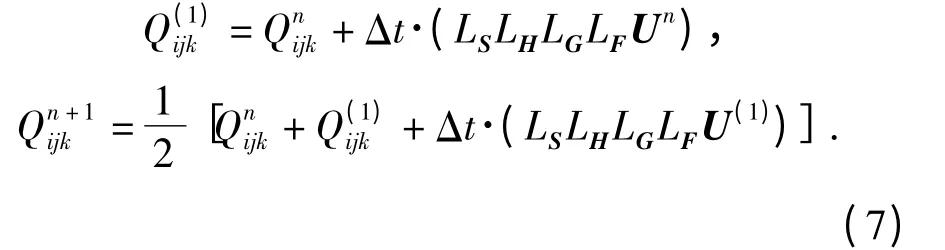
计算时，对流项采用无量纲量(无量纲的参考值为:压力p0=1 atm，温度T0=298.15 K，长度L0=1 m)，而化学反应项采用有量纲计算。

氢气－空气的燃烧采用9 种组分和19 个化学反应的基元反应模型，组分为H、O、H2、OH、H2O、O2、HO2、H2O2、N2［16］.

如图2所示爆轰燃烧室计算域示意图。燃烧室内径1.4L0，外径1.8L0，高度2.0L0.储气罐内储有等当量的氢气－空气预混气体，由上底面贴内壁注入燃烧室，注入宽度为0.2L0.

图2(b)为计算空间的初始流场，燃烧室中，点火区域Ω1内用C－J 爆轰阵面后的自模拟解来描述，其他区域，即:Ω2为p =1 atm 和T =300 K 的空气;Ω3为储气罐，为p=3 atm 和T=300 K 的可燃气。

上端面采用固壁边界条件，仅当压力低于储气罐压力时，才采用开口边界，以允许燃料注入。下端面采用自由出口边界条件，两端采用周期边界。储气室的网格数为ξ ×η ×ζ =30 ×800 ×100，燃烧室的网格数为ξ×η×ζ=60 ×800 ×200.

2 计算结果与讨论

旋转爆轰的扫描图像如图3所示。其中图3(a)为通过高速扫描照相机得到的实验扫描照片［5］，图3(b)是本文计算得到的扫描图像。两者符合的很好。

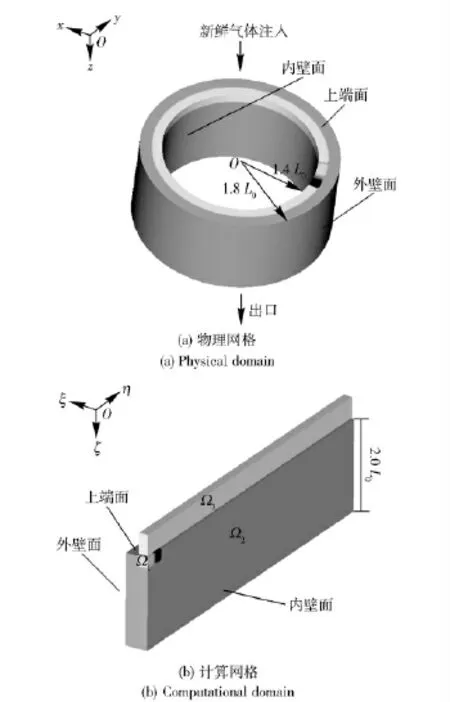
图2 计算区域示意图Fig.2 Schematic diagram of the computational model

图3 旋转爆轰扫描照片Fig.3 Streak pictures of rotating detonation

计算得到的存在旋转爆轰的燃烧室内的流场典型结构如图4所示。图4(a)对应于爆轰波的第1次循环，预混气从储气罐注入燃烧室，在上端面形成未燃气体层(图中区域I)。爆轰在可燃气层中传播，其阵面如图中曲线1 所示。图中区域II 为空气，爆轰波作用下，空气中形成透射激波，如图中曲线2 所示。由爆轰波和透射激波组成的复合波在区域I 和区域II 中传播［17］。波后爆轰产物(区域IV)与压缩空气(区域III)之间存在接触间断，用曲线3表示。图4(b)对应于爆轰波的第2 次循环。可燃气体层是在爆轰产物中形成的，如图中区域I，爆轰波(曲线1)在区域I 中传播。透射激波(曲线2)在爆轰产物(区域V)和空气(区域II)中传播。复合波波后由区域III、区域VI 和区域IV 组成。其中有2 条接触间断(图中曲线3 和4)，分隔空气、第1 循环的爆轰产物和第2 循环的爆轰产物。

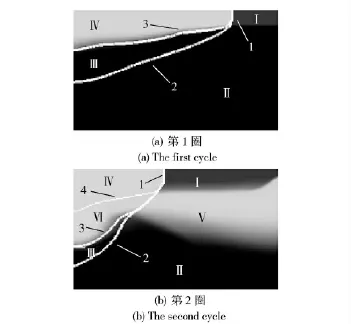
图4 燃烧室内的流场结构Fig.4 Flow field structure of inner wall in the combustion chamber

如图5所示某时刻爆轰燃烧室压力分布的三维结构图，深色区域表示爆轰波阵面，它仅出现在充满可燃物的靠近供气端的内环区域。由于爆轰波通过可燃气与空气的交界面，(包括外侧面和上侧面)，在空气中形成透射激波，上侧的透射激波传向管外，外侧的透射激波在燃烧室内、外壁来回反射，形成激波系列。爆轰波在燃烧室内传播时，其波前压力总是小于储气室的压力，故总有预混气注入，形成燃料层。因此，爆轰波可以在燃烧室内连续旋转。

爆轰波在同轴环形燃烧室内的连续传播，如图6所示描述了旋转爆轰波连续旋转的基本图像。

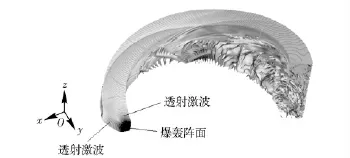
图5 旋转爆轰的三维结构Fig.5 Three－dimensional structure of rotating detonation

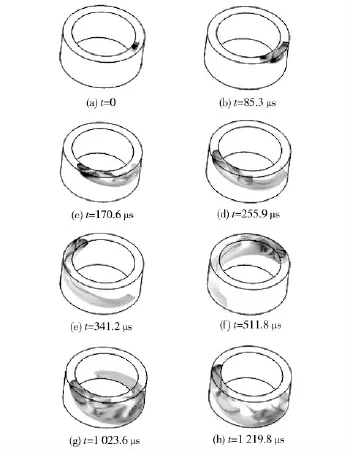
图6 旋转爆轰在燃烧室内的演化Fig.6 Evolutions of rotating detonation in annular chamber

侧向稀疏波从空气与爆轰波的接触处进入化学反应区，从而影响爆轰波的结构。如图7所示为爆轰波附近区域的OH 浓度分布图，用以反映爆轰反应区的宽度和形状。可见，沿着爆轰波阵面，由内壁向外壁，OH 的浓度下降，说明，侧向稀疏波影响下，反应速率下降。此外，爆轰波阵面是弯曲的，外侧的爆轰波传播速度低于内侧。

如图8所示爆轰波阵面不同径向截面上的压力剖面图。该图表明，爆轰强度随半径的增加而衰减，称此现象为侧向稀疏波影响下的爆轰亏损。

3 结论

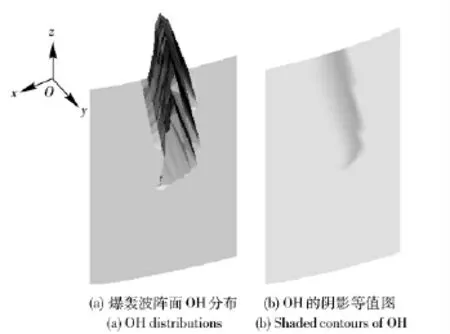
图7 t=511.8 μs 时刻爆轰波阵面在外壁面处OH质量分数分布Fig.7 Distribution of OH mass fraction on wall at t=511.8 μs

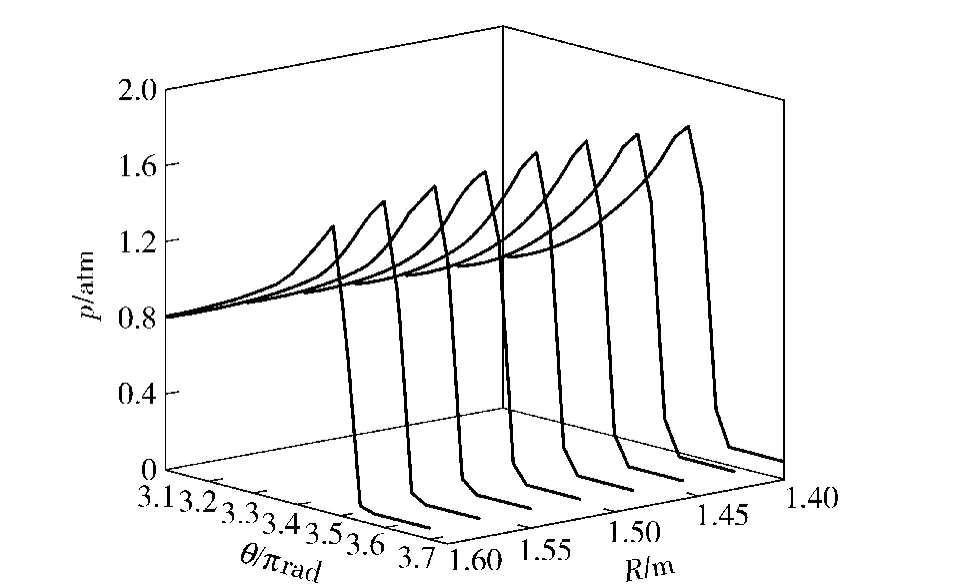
图8 爆轰波阵面压力的剖面图Fig.8 Pressure profiles along detonation front

基于带化学反应的三维Euler 方程，采用氢气－空气的9 组分19 步基元反应简化模型，对圆环形燃烧室内的旋转爆轰进行了数值模拟，数值计算结果与实验照片符合良好。

在三维同轴环形流场中，爆轰波紧贴燃料层传播。当储气室的压力大于燃烧室进气端面压力时，新的预混气就会的注入燃烧室，所以，爆轰波在环形燃烧室内能连续不断的循环传播。由于侧向稀疏波的影响，爆轰波在传播过程中会出现爆轰亏损现象。

References)

［1］ Roy G D，Frolov S M，Borisov A A，et al.Pulse detonation propulsion:challenges，current status and future perspective［J］.Progress in Energy and Combustion Science，2004，30:545－672.

［2］ Voitsekhovskii B V.Stationary detonation［J］.Doklady USSR Academy of Sciences，1959，129:1254－1256.

［3］ Nicholis J A，Dabora E K，Gealer R L.Studies in connection with stabilized gaseous detonation waves［C］∥Proceedings of the Combustion Institute.London:Elsevier，1959，7(1):766－772.

［4］ Bykovskii F A，Vedernikov E F.Continuous detonation combustion of an annular gas－mixture layer［J］.Combustion，Explosion，and Shock Waves，1996，32(5):489－491.

［5］ Bykovskii F A，Vedernikov E F.Continuous detonation of a subsonic flow of a propellant［J］.Combustion，Explosion，and Shock Waves，2003，39(3):323－334.

［6］ Bykovskii F A，Zhdan S A，Vedernikov E F.Continuous spin detonations［J］.Journal of Propulsion and Power，2006，22(6):1204－1216.

［7］ Bykovskii F A，Zhdan S A，Vedernikov E F.Continuous spin detonation of fuel－air mixtures［J］.Combustion，Explosion，and Shock Waves，2006，42(4):463－471.

［8］ Bykovskii F A，Zhdan S A，Vedernikov E F.Continuous spin detonation of hydrogen－oxygen mixture.1.annular cylindrical combustors［J］.Combustion，Explosion，and Shock Waves，2008，44(2):150－162.

［9］ Daniau E，Falempin F，Zhdan S.Pulsed and rotating detonation propulsion systems:first step toward operational engines，AIAA 2005－3233［R］.US:AZAA，2005.

［10］ Wolanski P，Kindracki J，Fujiwara T.An experimental study of small rotating detonation engine［C］∥Pulsed and Continuous Detonations.Russian:Torus Press，2006:332－338.

［11］ Falempin F，Daniau E.A contribution to the development of actual continuous detonation wave engine，AIAA 2008－2679［R］.US:AZAA，2008.

［12］ Zhdan S A，Bykovskii F A，Vedernikov E F.Mathematical modeling of a rotating detonation wave in a hydrogen－oxygen mixture［J］.Combustion，Explosion，and Shock Waves，2007，43(4):449－459.

［13］ Davidenko D M，Gökalp I，Kudryavtsev A N.Numerical study of the continuous wave rocket engine，AIAA 2008－2680［R］.US:AZAA，2008.

［14］ Hishida M，Fujiwara T，Wolanski P.Fundamentals of rotating detonation［J］.Shock Waves，2009，19(1):1－10.

［15］ Leveque R J.Wave propagation algorithms for multidimensional hyperbolic systems［J］.Journal of Computational Physics，1997，131(2):327－353.

［16］ Kee R J，Rupley F M，Miller J A.CHEMKIN－II:a fortran chemical kinetics package for the analysis of gas－phase chemical kinetics，SAND89－8009［R］.US:Sandia National Laboratories，1989.

［17］ Fujiwara T，Tsuge S.Quasi－one－dimensional analysis of gaseous free detonations［J］.Journal of the Physical Society of Japan，1972，33(1):237－241.